Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T15:54:07.236Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGORITHM TO CONSTRUCT INTEGRO SPLINES

Part of: Numerical approximation and computational geometry

Published online by Cambridge University Press:  13 September 2021

R. MIJIDDORJ Open the ORCID record for R. MIJIDDORJ [Opens in a new window]  and
T. ZHANLAV Open the ORCID record for T. ZHANLAV [Opens in a new window]
R. MIJIDDORJ*
Affiliation:
Department of Informatics, Mongolian National University of Education, Ulaanbaatar, Mongolia
T. ZHANLAV
Affiliation:
Institute of Mathematics and Digital Technology, Mongolian Academy of Sciences, Ulaanbaatar, Mongolia; e-mail: [email protected].
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study some properties of integro splines. Using these properties, we design an algorithm to construct splines 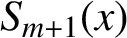$S_{m+1}(x)$ of neighbouring degrees to the given spline 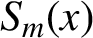$S_m(x)$ with degree m. A local integro-sextic spline is constructed with the proposed algorithm. The local integro splines work efficiently, that is, they have low computational complexity, and they are effective for use in real time. The construction of nonlocal integro splines usually leads to solving a system of linear equations with band matrices, which yields high computational costs.

Keywords

super-convergencenumerical integrationdifferentiation and integration operationspolynomial and nonpolynomialhistospline

MSC classification

Primary: 65D05: Interpolation
Type
Research Article
Information
The ANZIAM Journal , Volume 63 , Issue 3 , July 2021 , pp. 359 - 375
Check for updates
Copyright
© Australian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouch, C., Boujraf, A. and Tahrichi, M., “Superconvergent spline quasi-interpolants and an application to numerical integration”, Math. Comput. Simulation 137 (2017) 90–108; doi:10.1016/j.matcom.2016.09.014.CrossRefGoogle Scholar
Behforooz, H., “Approximation by integro cubic splines”, Appl. Math. Comput. 175 (2006) 8–15; doi:10.1016/j.amc.2005.07.066.Google Scholar
Boneva, L. I., Kendall, D. G. and Stefanov, I., “Spline transformations: three new diagnostic aids for the statistical data-analyst”, J. R. Stat. Soc. Ser. B Stat. Methodol. 33 (1971) 1–71, available at https://www.jstor.org/stable/2986005.Google Scholar
Boujraf, A., Tahrichi, M., Sbibih, D. and Tijini, A., “A simple method for constructing integro spline quasi-interpolants”, Math. Comput. Simulation 111 (2015) 36–47; doi:10.1016/j.matcom.2014.11.019.CrossRefGoogle Scholar
Burova, I. G. and Doronina, A. G., “On approximations by polynomial and nonpolynomial integro-differential splines”, Appl. Math. Sci. 10 (2016) 735–745; doi:10.12988/ams.2016.613.Google Scholar
de Boor, C., “A practical guide to splines”, in: Applied mathematical sciences, Volume 17 (eds Marsden, J. E. and Sirovich, L.) (Springer, New York, 1978) 243–261, available at https://www.springer.com/gp/book/9780387953663.Google Scholar
Keshi, F. K., Moghaddam, B. P. and Aghili, A., “A numerical approach for solving a class of variable-order fractional functional integral equations”, Comput. Appl. Math. 37 (2018) 4821–4834; doi:10.1007/s40314-018-0604-8.CrossRefGoogle Scholar
Kireev, V. I. and Biryukova, T. K., “Polynomial integro-differential 1D and 2D splines”, J. Comput. Technol. 3 (1998) 19–34, available at http://w.ict.nsc.ru/jct/annotation/111?l=eng.Google Scholar
Kobza, J., “Spline recurrences for quartic splines”, Acta Univ. Palacki. Olomuc. Fac. Rerum Natur. Math. 34 (1995) 75–89, available at http://eudml.org/doc/23614.Google Scholar
Lang, F. G. and Xu, X. P., “On integro quartic spline interpolation”, J. Comput. Appl. Math. 236 (2012) 4214–4226; doi:10.1016/j.cam.2012.05.017.CrossRefGoogle Scholar
Sakai, M. and Usmani, R. A., “Numerical integration formulas based on iterated cubic splines”, Computing 52 (1994) 309–314; doi:10.1007/BF02246511.CrossRefGoogle Scholar
Schoenberg, I. J., Cardinal spline interpolation, Volume 1 of CNBC-NSF Regional Conf. Ser. in Appl. Math. (SIAM, Philadelphia, PA, 1973); doi:10.1137/1.9781611970555.CrossRefGoogle Scholar
Siewer, R., “Histopolating splines”, J. Comput. Appl. Math. 220 (2008) 661–673; doi:10.1016/j.cam.2007.09.014.CrossRefGoogle Scholar
Wahba, G., “Interpolating spline methods for density estimation I. Equi-spaced knots”, Ann. Statist. 3 (1975) 30–48; doi:10.1214/aos/1176342998.CrossRefGoogle Scholar
Wang, R. H., Numerical approximation (Higher Education Press, Beijing, 1999), available at https://www.amazon.com/Numerical-Approximation-material-century-Chinese/dp/7040348322.Google Scholar
Wu, J. and Zhang, X., “Integro sextic spline interpolation and its super convergence”, Appl. Math. Comput. 219 (2013) 6431–6436; doi:10.1016/j.amc.2012.12.062.Google Scholar
Wu, J. and Zhang, X., “Integro quadratic spline interpolation”, Appl. Math. Model. 39 (2015) 2973–2980; doi:10.1016/j.apm.2014.11.015.CrossRefGoogle Scholar
Xu, X. P. and Lang, F. G., “Quintic B-spline method for function reconstruction from integral values of successive subintervals”, Numer. Algorithms 66 (2014) 223–240; doi:10.1007/s11075-013-9731-x.CrossRefGoogle Scholar
Zavyalov, Yu. S., Kvasov, B. I. and Miroshnichenko, V. L., Methods of spline functions (Nauka, Moscow, 1980), available at https://ua1lib.org/book/2409058/c2313a?id=2409058&secret=c2313a.Google Scholar
Zhanlav, T. and Mijiddorj, R., “On local integro quartic splines”, Appl. Math. Comput. 269 (2015) 301–307; doi:10.1016/j.amc.2015.07.077.Google Scholar
Zhanlav, T. and Mijiddorj, R., “A comparative analysis of local cubic splines”, Comput. Appl. Math. 37 (2018) 5576–5586; doi:10.1007/s40314-018-0651-1.CrossRefGoogle Scholar
Zhanlav, T. and Mijiddorj, R., “Integro cubic splines on non-uniform grids and their properties”, East Asian J. Appl. Math. 11 (2021) 406–420; doi:10.4208/eajam.030920.251220.Google Scholar
Zhanlav, T., Mijiddorj, R. and Behforooz, H., “Construction of local integro quintic splines”, Commun. Numer. Anal. 2 (2016) 167–179; doi:10.5899/2016/CNA-00267.CrossRefGoogle Scholar