Introduction
Metal objects of regulated mass are a well-known phenomenon of European prehistory. A recent study of over 3000 bronze objects in European hoards has shown that they were fragmented into pieces of specific, regulated mass values in accordance with the metrological system of European Bronze Age balance weights (Ialongo & Lago Reference Ialongo and Lago2021). Mass-regulation can also be found in hacksilver from early second-millennium BC Mesopotamia, where extensive written evidence has shown that silver was sometimes exchanged directly for goods and that the precious metal served as a general reference value in the economic framework of the ancient Near East (Pomponio Reference Pomponio, Camilli and Sorda2003; Peyronel Reference Peyronel, Matthiae, Pinnock, Nigro and Marchetti2010). These texts suggest that other materials, such as barley or copper, were also used as exchange items (e.g. Gelb et al. Reference Gelb, Steinkeller and Whiting1991; Powell Reference Powell1996). A recent comparative study of silver scrap hoards from Ebla (Syria), Kültepe (Turkey) and Ur and Larsa (Iraq) indicates that silver was fragmented according to the same metrological system as Mesopotamian balance weights (Ialongo et al. Reference Ialongo, Vacca and Peyronel2018). In Late Bronze Age Mycenae, gold was weighed and regularly used in transactions (Zurbach Reference Zurbach, Rahmstorf, Barjamovic and Ialongo2021). In all these cases, the evidence suggests that mass-regulated fragments were probably used as currency.
The assumption that some Bronze Age metal objects were mass-regulated is not new. De Rossi (Reference De Rossi1886) suggested that bronze was produced in accordance with certain mass values. Hawkes (Reference Hawkes1932) noted that eight of the nine artefacts in the Towednack gold hoard (Cornwall, UK), comprising gold bar torcs and penannular bracelets, appeared to fall into three ‘groups’ of masses: around 20–30g, 62–63g and 94–96g. The ninth object, weighing 47.9g, was the only artefact not adhering to that standard, but Hawkes recognised its mass as half of the heaviest group of objects, even going so far as to suggest that “these facts may possibly find importance in some future metrological study of prehistoric gold weights …” (Hawkes Reference Hawkes1932: 180). Northover (Reference Northover1989: 125–26) later identified different mass clusters for gold bar torcs, and Meeks and Varndell (Reference Meeks and Varndell1994: 2) determined that, in some cases, gold torcs were broken into fragments of (more or less) equal mass. Subsequently, Ruiz-Gálvez (Reference Ruiz-Gálvez and Pare2000: 271) has proposed a standard unit of 11.75g for gold torcs, based on calculations of 45 torcs from France and the British Isles. Gwilt et al. (Reference Gwilt, Kucharski, Silvester and Davis2005: 45–51) have suggested that bracelet fragments, such as those in the Rossett Hoard from North Wales, as well as finger ingots, could have been regulated by mass or size. All these studies, however, have used descriptive metrological methods, which essentially consist of multiple attempts at matching the numbers to certain patterns.
In a recent study of Bronze Age weights and potential mass-regulated objects published in this journal, Rahmstorf (Reference Rahmstorf2019) applied statistical analysis to 52 British gold bar torcs and 100 penannular bracelets and dress-fasteners from Britain, Ireland and France. Using Cosine Quantogram Analysis (CQA), a method originally developed by Kendall (Reference Kendall1974), and tested for statistical significance through Monte Carlo simulation, Rahmstorf (Reference Rahmstorf2019: 1203) shows that the objects could be divided into three statistically relevant ranges of mass: 11.6–11.9g, 41–46g and 90–97g. Unlike the specific unit suggested by Ruiz-Gálvez (Reference Ruiz-Gálvez and Pare2000), a range of mass per unit seems more likely, as prehistoric objects such as balance weights always display some mass variation, even when they apparently adhere to certain groups.
While Rahmstorf's ground-breaking approach to metrological analysis has paved the way for further studies on the subject, it has thus far only been applied to a limited range of object types. The analysis was undertaken as part of the ERC-funded WEIGHTANDVALUE project, which has since collected further data on British Bronze Age gold objects. In line with good scientific practice to reanalyse new data as they emerge, and in order to gain a better understanding of British Bronze Age gold and its place within the European prehistoric trading network, it was decided to (re-)analyse the bar torcs, penannular bracelets and dress-fasteners within the context of a wider variety of other gold objects, such as ribbon torcs, sleeve-fasteners, lunulae and various gold rings. This article uses CQA and Monte Carlo simulations to analyse this range of Bronze Age gold objects from the British Isles to evaluate if, and how, these artefacts were mass-regulated.
Method and data
Methodology
CQA as a means to study balance weights and mass-regulated items is now the established method for ancient weight metrology (e.g. Petruso Reference Petruso1992; Pare Reference Pare1999; Hafford Reference Hafford2005, Reference Hafford2012; Rahmstorf Reference Rahmstorf, Morley and Renfrew2010; Ialongo Reference Ialongo2018; Ialongo et al. Reference Ialongo, Vacca and Peyronel2018). Since it has been described by others (e.g. Petruso Reference Petruso1992; Pare Reference Pare1999: 487–88; Ialongo Reference Ialongo2018: 107–109), the method will not be reiterated in detail here. Briefly, however, Kendall's (Reference Kendall1974) formula is used to find common divisors (so-called ‘quanta’) from a range of data, while allowing some small deviation. The formula was specifically designed for mathematical analysis of archaeological features (Kendall Reference Kendall1974), so a certain amount of inaccuracy was assumed. Expressed as a graph on a Cartesian coordinate system, the y-axis extent (peak) shows how well the data fit each proposed quantum (x-axis). Generally, the higher the peak the better the quantum. Monte Carlo simulations are then used to test the results for statistical significance against 1000 similar, randomly generated samples. In order to achieve statistical significance, the graph must demonstrate results better than 95 per cent of the simulated random samples. On the coordinate system, this is expressed as a horizontal line. Any peaks scoring higher than the line are statistically significant.
When dealing with large samples, it is necessary to first break the data into smaller ranges that can be analysed individually. This is best done via Frequency Distribution Analysis (FDA), in which a histogram is used to identify natural gaps, drops or mass clusters. The gaps define the range limits. A histogram of Bronze Age Aeolian, Central European, Italian and Sardinian balance weights, for example, shows neat clusters around 4g, 8g, 16g, 20g, 40g, 50g, 60g and 80g (Figure 1).
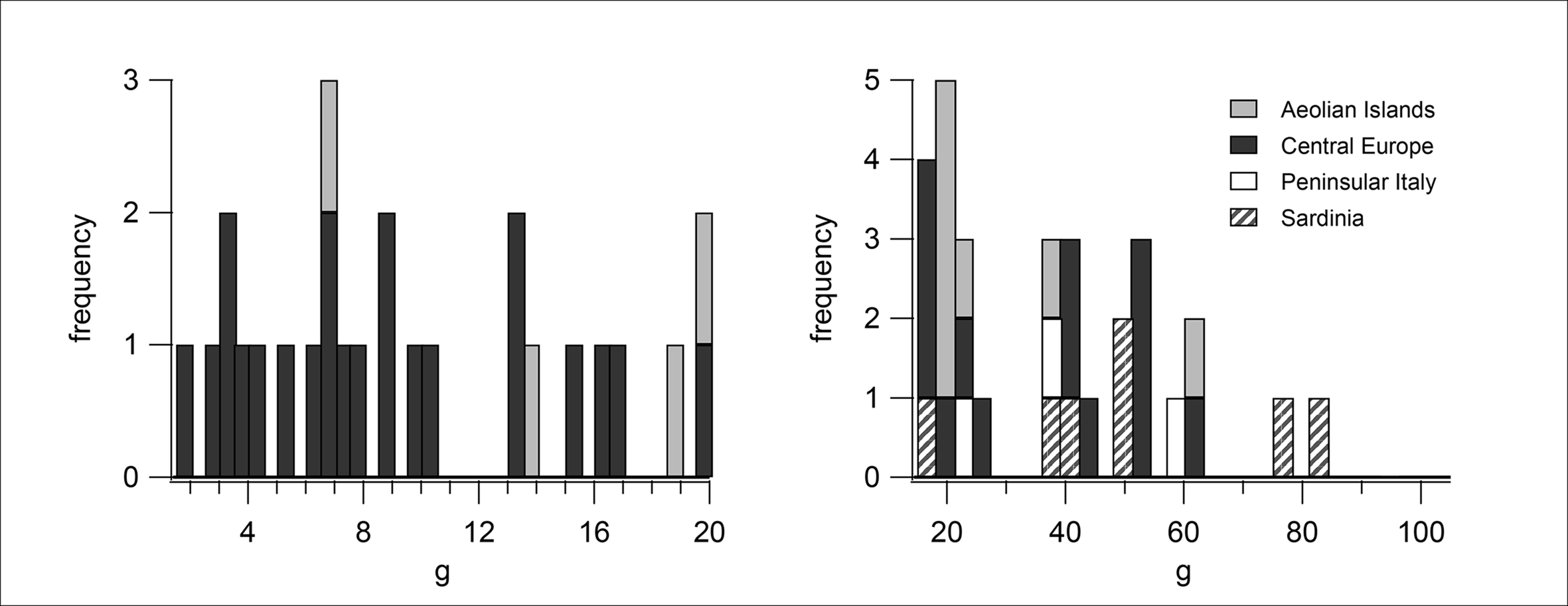
Figure 1. Frequency distribution analysis of weight-regulated Bronze Age balance weights, showing clusters at regular intervals (data from Ialongo Reference Ialongo2018: 113 & fig. 7A).
When using mathematical analysis to test for mass-regulation in Bronze Age gold objects, it is imperative to understand how the results are created and how they should be interpreted. Technically, CQA cannot determine whether the objects were regulated; the analysis can only be used to prove or disprove a hypothesis. Like most statistical tests, CQA works on a null hypothesis. In this case, the null hypothesis is that the sample is not quantally configured (i.e. it is randomly constituted), meaning that Bronze Age gold objects were not regulated by mass. Based on this, the results should display a random configuration without statistically relevant high peaks at regular intervals. If the opposite is true, the sample should display a quantal configuration (i.e. statistically relevant peaks at regular intervals); Figure 2, with extremely high peaks reaching 20 on the y-axis, with multiple peaks at, for example, 50g (1), 25g (1/2) and 12.5g (1/4), illustrates this. Additionally, FDA should show neat clusters around the same values. If neither is the case, the null hypothesis is true, and the objects were not regulated. If both a quantal configuration and neat FDA clusters are displayed, then the null hypothesis is rejected and the objects were most probably regulated by mass, or by another factor such as size, which can ultimately be correlated with the mass.
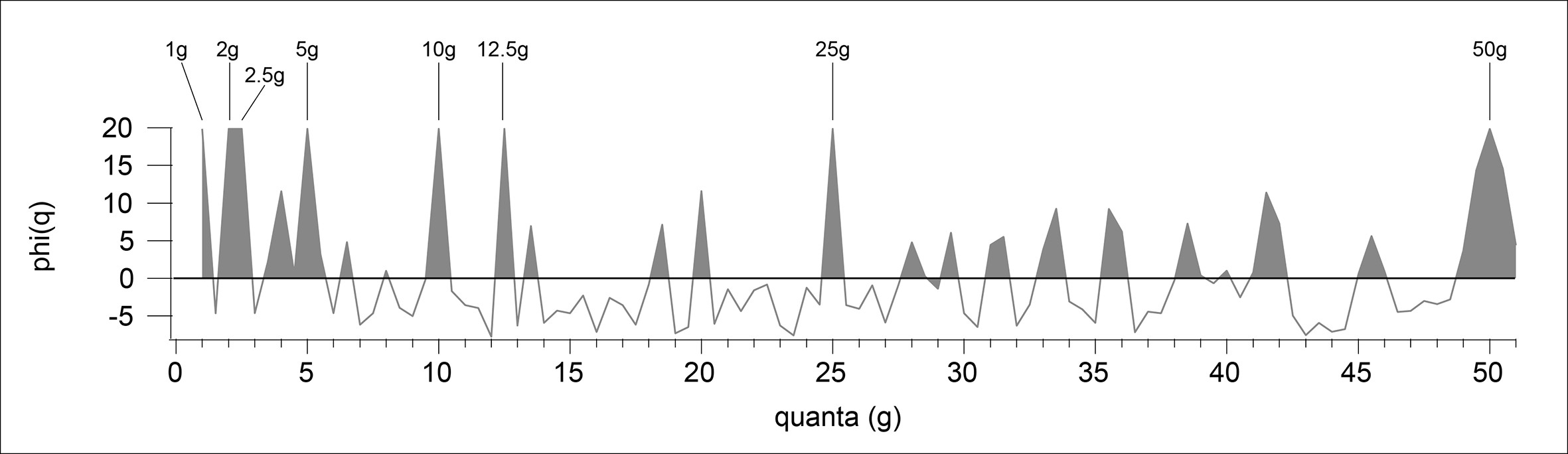
Figure 2. Cosine Quantogram Analysis of weight-regulated supermarket items, showing a statistically relevant quantal regulation, with high peaks at regular intervals (data from Ialongo Reference Ialongo2018: 108 & fig. 2; Ialongo & Vanzetti Reference Ialongo, Vanzetti, Biagetti and Lugli2016).
Data
The typology of Bronze Age gold artefacts, the timeline of which is illustrated in Figure 3, has long been discussed, with notable works by Taylor (Reference Taylor1980) and Eogan (Reference Eogan1994). Statistical analysis is most viable when applied to large datasets, and hence the nine most frequently encountered object classes—lunulae, sleeve-fasteners, dress-fasteners, penannular bracelets, rings (ring-money, striated rings, lock rings), bar torcs and ribbon torcs (Figure 4)—are used for this study. While these can be subdivided into regional subtypes, for the purpose of this research, the subtypes were analysed in aggregate. The terminology used to describe the objects follows Murgia et al.'s (Reference Murgia, Melkonian and Roberts2014) European Bronze Age gold in the British Museum catalogue. Their terminology spans the entire period (and potentially on into the Iron Age), beginning with Early Bronze Age lunulae and ending with Late Bronze Age bracelets and fasteners (Figure 3). The dataset covers a period of around 1600 years, with an increase in the quantity of objects towards the Late Bronze Age. This large temporal spread enables the identification of any potential chronological developments of mass-regulation during this period.

Figure 3. Approximate timeline (c. 2400–600 BC) for European Bronze Age gold objects (absolute dates after Murgia et al. Reference Murgia, Melkonian and Roberts2014).

Figure 4. The nine classes of gold objects analysed. All objects are in the British Museum collection (accession numbers in parentheses). From top left to bottom right: lunula (1869,0619.19); bar torc (1838,0128.1); sleeve-fastener (1871,0401.7); striated ring (1874,0303.5); ring-money (1996,0902.37); lock ring (WG.25); dress-fastener (1834,1222.1); penannular bracelet (1838,0718.2) and ribbon torc (1921,0621.2) (scale in cm; images © The Trustees of the British Museum, reproduced under Creative Commons license CC BY-NC-SA 4.0).
Data collection
In total, 1094 gold objects from the British Isles were collected in a database. Most of the information stems from Taylor (Reference Taylor1980) and Eogan (Reference Eogan1994). Information on more recent finds was mostly obtained from the Portable Antiquities Scheme (finds.org.uk). As mass values were not given for many objects, English, Scottish and Irish museums were visited in order to weigh these objects. Other museums were contacted and asked to weigh individual objects. Weighing was usually conducted using Kern 572 high-precision scales. Objects were divided into 781 complete, 85 fragmented and 228 specimens of unknown state or preservation (Table S1 in the online supplementary material (OSM)). In total, it was possible to record mass values for 863 specimens, ranging from 0.71–1353g (all raw data are available in the OSM).
The artefacts
Lunulae are flat, crescent-shaped sheets of gold, thought to have been worn as neck or head ornaments (e.g. Eogan Reference Eogan1994: 34), although there is no contextual evidence for this. Lunula subtypes can be classified as classic, plain, unaccomplished or provincial (Taylor Reference Taylor1980: 28–33; Eogan Reference Eogan1994: 30–32). Usually dated to the Early Bronze Age (Eogan Reference Eogan1994: 33–34), their decoration has often been interpreted as a continuation of that found on Beaker pottery (Taylor Reference Taylor1970: 56–62, Reference Taylor1980: 14) and spacer-plate jet necklaces in northern England and Scotland (Howarth Reference Howarth1899: 57–64; Sheppard Reference Sheppard1929: 106; Morrison Reference Morrison1979); Lunulae are particularly common in Ireland (Eogan Reference Eogan1994: 37).
Bar torcs consist of a bar with a square cross-section, and are usually finished with bent-back terminals that are frequently slightly expanded in a ‘trumpet’ shape. The bar is twisted, often in a clockwise manner (Eogan Reference Eogan1994: 56). A study by Hautenauve and Besson (Reference Hautenauve and Besson1998: 147 & fig. 8), however, has shown that instead of a simple twist, the torc is often split and hammered into multiple flanges, which are then turned. Torcs were often bent into a large ring or coiled (see Figure 4) and could have been worn as personal ornaments. The recently discovered Ely gold torc (PAS CAM-E5D871) is so large (1.265m long) that it could have been worn around the waist.
How sleeve- (or cuff-) fasteners (Hawkes & Clarke Reference Hawkes, Clarke, Foster and Alcock1963: 223; Taylor Reference Taylor1980: 68) were used is unknown (Eogan Reference Eogan1994: 88), but a function as a device securing a garment seems possible. Generally small, they comprise an arched body with flat discs attached to each terminal. Striated rings are similar in shape and decoration, with tapering and cross-hatched terminals (Eogan Reference Eogan1994: 89), but without the terminal discs. Both sleeve-fasteners and striated rings occur only in Ireland.
The so-called ring-money is a type of penannular ring that can be made of solid gold or a core (e.g. of lead) covered with gold foil. As the term suggests, the objects have been considered a type of proto-currency (e.g. Taylor Reference Taylor1980: 65). It is, however, almost impossible to identify the exact composition of every individual piece—a problem Bronze Age users would also have faced. If these objects were used as currency, foil-covered cores could represent a type of early counterfeit money. Alternatively, the objects could have been used as a hair ornament, like the lock rings, which are hollow, penannular objects with a triangular cross-section, named after their presumed purpose (Varndell Reference Varndell2001: 515). These occur in Ireland, Britain and France (Eogan Reference Eogan1994: 89).
Dress-fasteners usually consist of a broadly curved body with a circular cross-section, and expanded, often hollow and occasionally decorated terminals (Eogan Reference Eogan1994: 88). Typologically, they strongly resemble the penannular bracelets, which consist of the same curved body with (mostly) circular cross-sections but with smaller, trumpet-shaped, expanded terminals. Taylor (Reference Taylor1980: 66) summarised both object types under the term ‘bracelets and cup-ended ornaments’. In the present study, dress-fasteners and penannular bracelets were analysed jointly.
Ribbon torcs have long been a subject of discussion in prehistoric archaeology. With some 120 specimens known, they were traditionally dated to the Middle Bronze Age (Taylor Reference Taylor1980: 63–65; Eogan Reference Eogan1994: 53). Although often considered simple, flat bands twisted into shape, goldsmith Brian Clarke (Reference Clarke2014) has shown that they required a complex technique called ‘anticlastic raising’. Moreover, recent studies by Hunter (Reference Hunter, Schwab, Milcent, Armbruster and Pernicka2018) and Warner (Reference Warner and Fenwick2003, Reference Warner and Roche2004) have argued convincingly that many of the presumed Bronze Age ribbon torcs date to the Iron Age, citing marked typological and compositional differences. Typologically, Warner attributes ribbon torcs with loose twists and plain, hooked terminals (Class 1) to the Middle Bronze Age, and tighter twisted torcs with expanded or knobbed terminals (Class 2) to the Iron Age (Warner Reference Warner and Fenwick2003: 152). Compositionally, Iron Age ribbon torcs contain notably higher quantities of silver, copper and tin (Warner Reference Warner and Fenwick2003: 160) than their Middle Bronze Age predecessors. Based on available contextual, typological and compositional (after Hartmann Reference Hartmann1970) data, the 124 ribbon torcs collected for the present study are divided into 38 Class 1 (Middle Bronze Age), 53 Class 2 (Iron Age) and 33 unclassified objects. To avoid the possibility of including any objects with potential Iron Age mass-regulation, only the 38 Class 1 ribbon torcs are included in the present analysis.
Analysis
The wide spread of values makes it imperative to identify smaller ranges for analysis. FDA of 810 specimens shows a drop in frequency at around 60g and a large gap above 410g (Figure 5; mass values greater than 800g are not shown on the graph). Thus a ‘light’ range between >0 and 60g and a ‘heavy’ range between 60 and 410g were identified, with specimens with a greater mass removed as outliers. FDA diagrams and CQA graphs were then created for each range and for the individual object classes in each range. Working on the assumption that these objects were mass-regulated, we would expect to see regular, statistically significant CQA peaks and distinct FDA clusters similar to those in Figures 1 and 2.
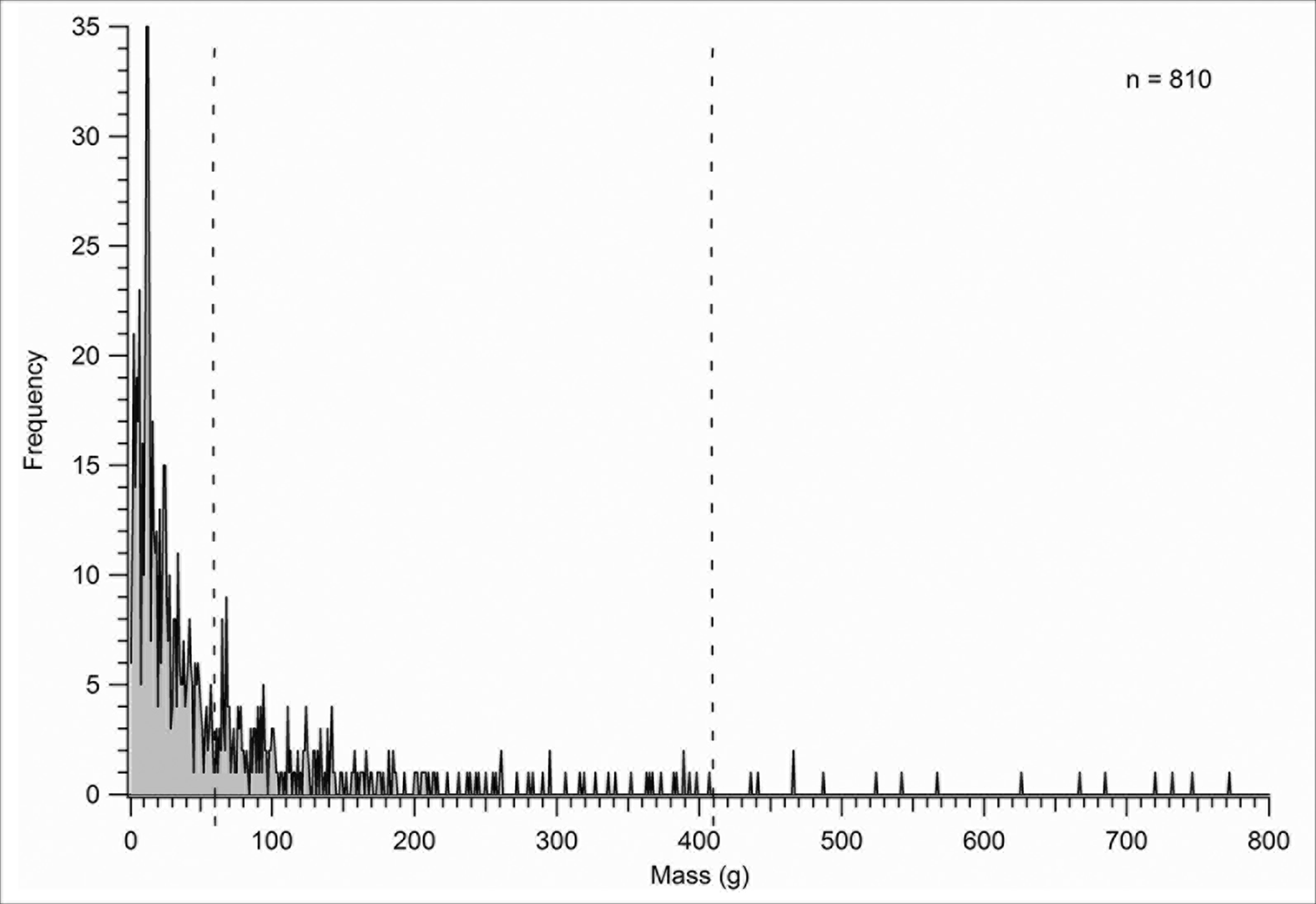
Figure 5. Frequency Distribution Analysis of 810 gold artefacts, with gaps at 60g and 410g (highlighted by dotted lines) (figure by the author).
Light range
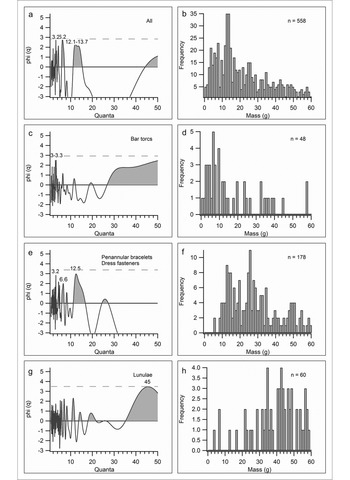
The light range contains most of the artefacts (n = 558) and includes objects of all classes. Initially, the light objects were analysed together, and then as individual object classes. As there are only 23 light lock rings, these were not analysed separately. The fragmented examples of various objects were included in the analysis. Finally, the 53 ‘light’ fragments were analysed separately to test for hackgold.
The joint analysis of all 558 objects displays a number of high peaks, specifically at 3.2, 6.2 and 12.1–13.7, the first two of which approach the statistical significance line (Figure 6: a). The FDA diagram (Figure 6: b) shows a large concentration of values around 11–13g, two smaller concentrations slightly above and below 5g, and one around 25g. The CQA peaks seem to correlate with these clusters, which, although not statistically significant, may suggest some sort of underlying quantal configuration. The results, however, are unclear. The analysis of 48 gold bar torcs shows a single higher peak at 3–3.3 and a range increasing towards infinity (Figure 6: c). The single peak does not touch the statistical significance line. No regulated cluster could be detected on the FDA (Figure 6: d).
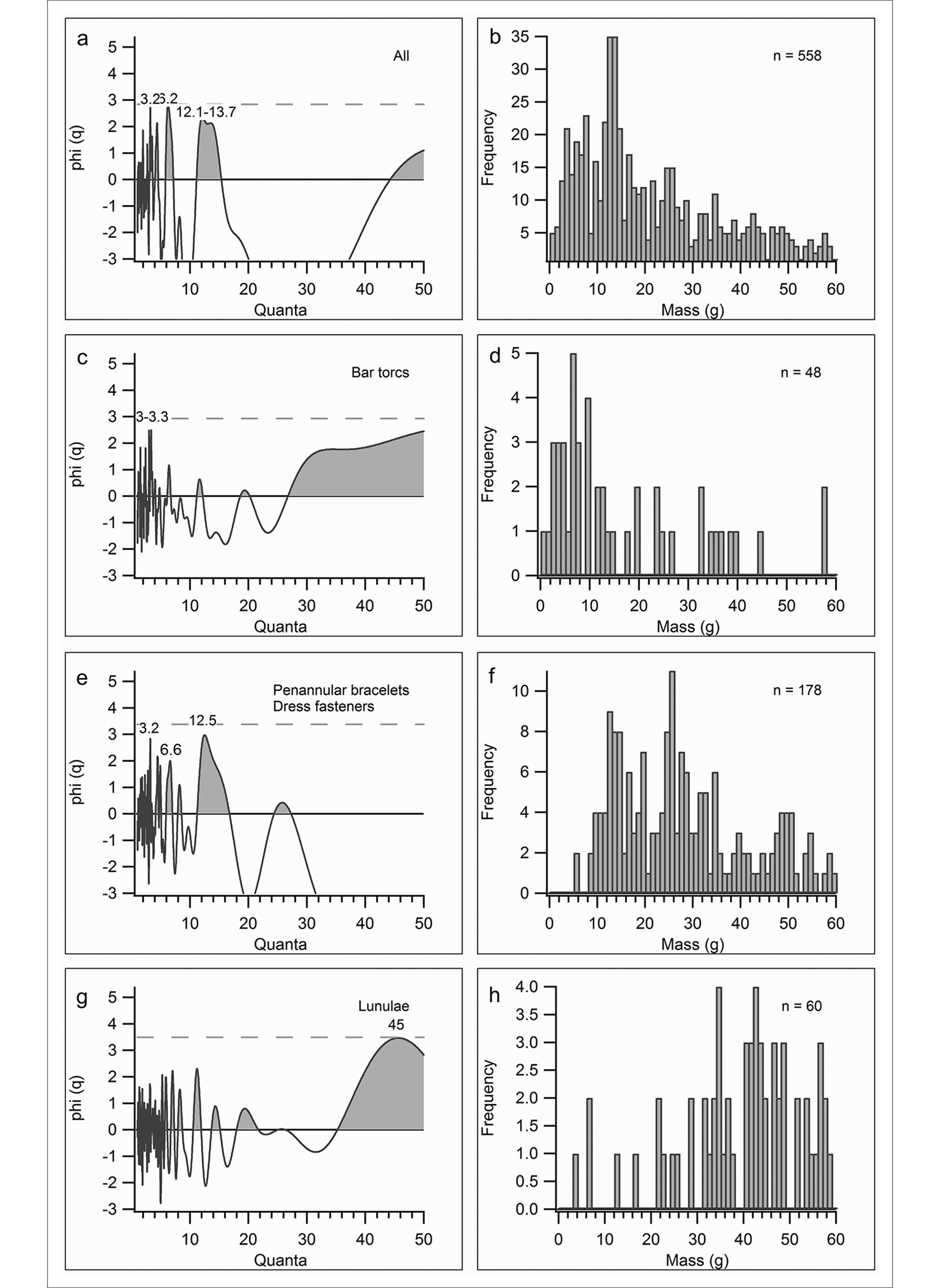
Figure 6. ‘Light’ range Cosine Quantogram Analysis (CQA) graphs and Frequency Distribution Analysis (FDA) diagrams of: ‘all’ (a: CQA; b: FDA); bar torcs (c: CQA; d: FDA); penannular bracelets/dress-fasteners (e: CQA; f: FDA); and lunulae (g: CQA; h: FDA) between 0g and 60g (figure by the author).
Analysed jointly, given their typological similarities, the 178 penannular bracelets and dress-fasteners display seemingly multiple peaks at 3.2, 6.6 and 12.5 (Figure 6: e), none of which, however, are statistically significant. The FDA appears to show approximate clusters around 12–15g, 25g and 50g (Figure 6: f), but neither the CQA peaks nor the FDA clusters are sufficiently regular and neat to suggest a quantal configuration.
Lunulae display a wide, rounded curve, which touches the statistical significance line at 45 (Figure 6: g), but no other related peaks are visible on the quantogram. The FDA reveals that the wide curve is the result of a concentration of lunulae with a mass around 35–60g (Figure 6: h). No other clusters could be detected.
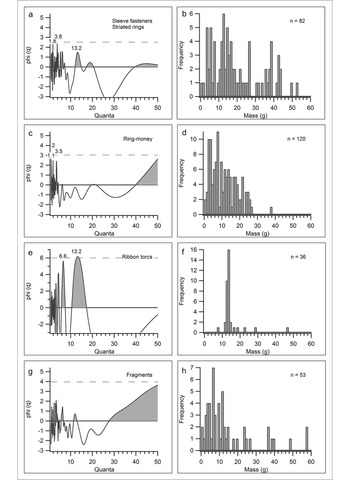
The analysis of 82 sleeve-fasteners and striated rings shows two peaks at 1.8 and 3.8, as well as a somewhat wider peak at 13.2; none of these reach the statistical significance line (Figure 7: a). The FDA displays a concentration of masses around these values (Figure 7: b). No quantal configuration could be detected.
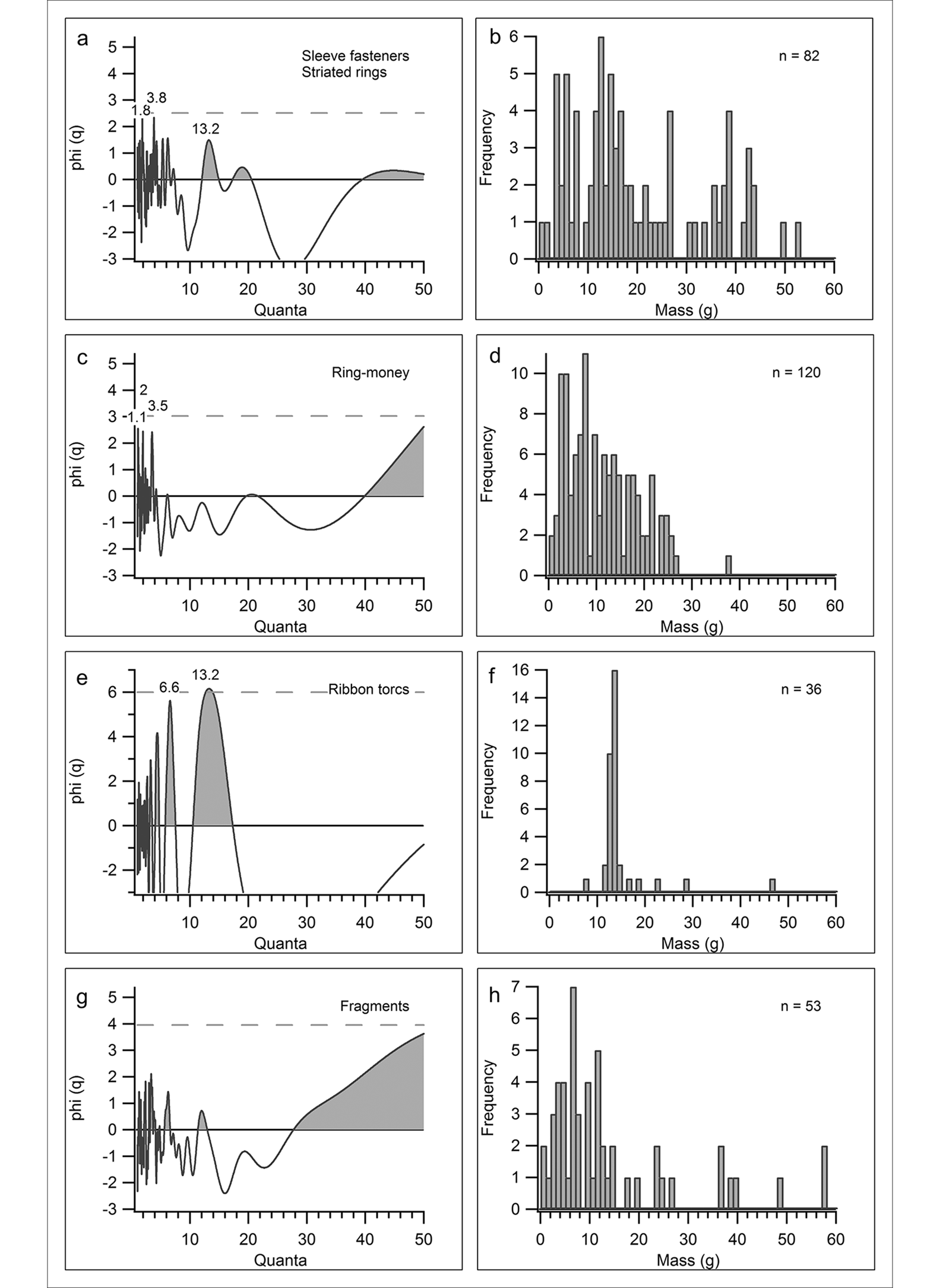
Figure 7. ‘Light’ range CQA graphs and FDA diagrams continued from Figure 6: sleeve-fasteners (a: CQA; b: FDA); ring-money (c: CQA; d: FDA); ribbon torcs (e: CQA; f: FDA); and fragments (g: CQA; h: FDA: h) between 0g and 60g (figure by the author).
Analysis of the 120 ring-money artefacts shows small peaks at 1.1, 2 and 3.5, and a curve towards infinity, none of which are statistically significant (Figure 7: c). The FDA diagram shows concentrations of mass values around 3g and 8g, but no neat, repeating clusters (Figure 7: d). Analysis of 36 Class 1 ribbon torcs shows high peaks at 6.6 and 13.2, along with several smaller peaks (Figure 7: e). Whilst the highest peak touches the statistical significance line, the peak at 6.6 appears to be a false positive, as revealed by the FDA diagram, which only shows a (strong) concentration of values around 13g (Figure 7: f). Although there is no quantal configuration for these artefacts, the high concentration of similarly weighted objects is noteworthy.
Finally, the 53 fragments (from all object classes) display no high peaks and a range towards infinity (Figure 7: g). The FDA diagram displays a large concentration of object masses between 3g and 12g and smaller numbers of heavier fragments (Figure 7: h). There is no quantal configuration detectable for the gold fragments.
Heavy range
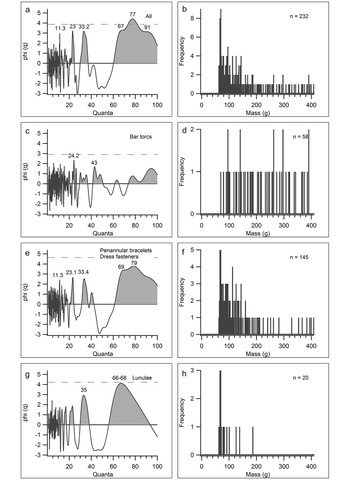
Since few or no heavy objects were present in certain categories, only four object classes were included in the heavy range (between 60g and 410g): penannular bracelets, dress fasteners, bar torcs and lunulae. Again, the fragmented ‘heavy’ gold objects were included in the analysis. As there are only 14 fragmented specimens in this range, they were not analysed separately.
The joint analysis of all 232 heavy gold objects shows a statistically significant curve peaking at 77, as well as several other peaks at, for example, 11.3, 23.0 and 33.2 (Figure 8: a). The FDA reveals that the wide curve is due to a large concentration of masses around those values, rather than a quantal configuration. There are no further clusters present (Figure 8: b).

Figure 8. ‘Heavy’ range CQA graphs and FDA diagrams of: ‘all’ (a: CQA; b: FDA); bar torcs (c: CQA; d: FDA); penannular bracelets/dress-fasteners (e: CQA; f: FDA); and lunulae (g: CQA; h: FDA) between 60g and 410g (figure by the author).
The 58 heavy bar torcs display peaks at 43 and approximately 24.2, as shown by Rahmstorf (Reference Rahmstorf2019: fig. 5), but the current analysis suggests that these are not statistically significant (Figure 8: c). The FDA diagram shows a very even distribution of mass values between 60g and 410g, with no visible clusters (Figure 8: d). A quantal configuration is not present.
The 145 penannular bracelets and dress fasteners analysed together create a CQA graph very similar to that of all the heavy gold objects: a wide curve, with a peak around 79, as well as some smaller peaks at 11.3, 23.1 and 33.4. None of the peaks reach the statistical significance line (Figure 8: e). Again, the wide curve is the result of a large concentration of mass values around 80g (Figure 8: f). No quantal configuration can be detected.
The CQA graph of the 20 heavy lunulae displays a large curve around 66–68, which terminates just below the line of statistical significance (Figure 8: g). The second highest peak at 33 gives the impression of a quantal configuration (1/2), although the FDA diagram reveals that this is simply due to a concentration of values around 70g (Figure 8: h), and hence no real quantal configuration is present.
Discussion
The mass-regulation of certain Bronze Age gold objects has been suggested in the past (e.g. Hawkes Reference Hawkes1932; Northover Reference Northover1989) and was recently seemingly confirmed through CQA by Rahmstorf (Reference Rahmstorf2019). The aim of the present study is to verify the hypothesis that Bronze Age gold objects from Britain were regulated by mass. To do so, the mass values of 810 of the most commonly encountered gold objects (bar torcs, ribbon torcs, penannular bracelets, dress-fasteners, sleeve-fasteners, lunulae and various rings) were analysed by CQA and FDA. To confirm the hypothesis, the CQA analysis should display a statistically relevant quantal configuration, with high peaks at regular intervals, as well as neat clusters on the FDA diagram. This type of configuration can be seen, for example, in contemporaneous European balance weights, hoarded bronze fragments, or Mesopotamian silver (Pare Reference Pare1999; Ialongo Reference Ialongo2018; Ialongo et al. Reference Ialongo, Vacca and Peyronel2018; Ialongo & Lago Reference Ialongo and Lago2021).
The gold objects analysed here range in mass values from less than 1g to over 1.3kg. The data were therefore split into two smaller mass ranges of 0–60g and 60–410g. Any higher values were removed as statistical outliers. For each range, the mass values were analysed in aggregate, as well as for each individual object class. The typologically similar penannular bracelets and dress-fasteners were analysed together. ‘Light’ fragments were also analysed. The analysis of the ‘heavy’ range of artefacts excluded rings, sleeve fasteners and ribbon torcs, as these objects were not sufficiently heavy.
The analysis has shown that there are certain commonly shared mass values across some object categories, but the Monte Carlo simulation shows that these values are either false positives, or that there is a hidden pattern that is blurred by a large quantity of non-regulated objects. Statistically speaking, the quantal hypothesis thus cannot be supported. Archaeologically speaking, this could mean that most British Bronze Age gold objects were not regulated by mass, but that a minority may have been somewhat regulated. Surprisingly, the quantal configuration discovered by Rahmstorf (Reference Rahmstorf2019)—based on a sample of 52 bar torcs and 100 penannular bracelets/dress-fasteners—could not be confirmed by the larger sample used in this study. Although the significant values in Rahmstorf's (Reference Rahmstorf2019) analysis are similar to the results presented here, these values are no longer statistically significant when analysing a larger dataset. This contrast requires some explanation: Rahmstorf analysed 52 complete bar torcs with mass values above 80g, with five lighter torcs deemed outliers and omitted from the analysis (Rahmstorf Reference Rahmstorf2019: 1203). His sample contained seven French specimens that were not included here. Rahmstorf also used different mass values for a torc from Hampton/Malpas (with an incorrect mass value taken from Eogan (Reference Eogan1994: 128) that was subsequently reweighed by the present author) and for a torc from Ysgeifiog that was published with different weight values (754g in Northover Reference Northover1989: 136; 772.92g in Eogan Reference Eogan1994: 129; for a full comparison between Rahmstorf's and the present study's data, see the OSM).
As Rahmstorf's (Reference Rahmstorf2019) article did not include a list of the penannular bracelets/dress-fasteners he analysed, no direct comparison with the data used here can be presented. The present sample, however, is significantly larger than Rahmstorf's 100 specimens. Rahmstorf's CQA analysis scored higher than the 5 per cent statistical significance line, thus making his results statistically significant. Nevertheless, this could also mean that there is a 5 per cent probability that the positive results are a coincidence (this is explained in more detail by Rahmstorf (Reference Rahmstorf2019: 1203)). At the time, and with the dataset available, Rahmstorf's data and interpretation were correct. Following the collection of further data, and a reanalysis of the new, enlarged dataset, the results presented here no longer support that interpretation.
As mentioned, the presence of certain shared values may indicate that some individual objects, or small groups of objects, were manufactured or collected in accordance with a specific mass, size or other (unknown) factor. The Towednack Hoard gold objects, for example, clearly fall into three or four seemingly regulated groups, but whether this is deliberate or coincidental remains uncertain. In Wales, the four Rossett Hoard bracelet fragments are of similar length, diameter and masses (Gwilt et al. Reference Gwilt, Kucharski, Silvester and Davis2005). In Spain, the Bodonal de la Sierra gold hoard includes 15 bar torc fragments with terminals almost identical in shape and size (Almagro Gorbea Reference Almagro Gorbea1974: figs 1–2), nine of which have similar masses of around 70g. It seems reasonable to suggest that the terminals were either deliberately fragmented into similar shapes/sizes/masses, or that, at least, fragments of similar shapes/sizes/masses were grouped together for inclusion in the hoard. It seems, therefore, that some regulation did exist—at least within individual hoards. Controlling the mass of fragments is significantly more difficult than controlling other variables, such as size or length, and requires balance scales and weights, and the skills to use them. Simply cutting off a certain length of material or quartering an object (i.e. breaking the object in two, then halving each half), as suggested for the Rossett fragments (Gwilt et al. Reference Gwilt, Kucharski, Silvester and Davis2005: 46), is inherently easier to achieve. It is thus doubtful that mass was the regulating factor in these instances.
The large concentrations around some mass values of individual object classes, such as sleeve-fasteners (13g), rings (5g), ribbon torcs (13g), penannular bracelets/dress fasteners (80g) and lunulae (70g), are notable. While this could be intentional—certainly for smaller items, such as sleeve-fasteners and rings—there may be a more practical explanation. Rings worn as hair adornments, for example, will naturally fall into a certain size range. Although there will be variations, these will be too small to show as different mass values. Any ‘regulation’ is therefore probably not by mass, but by size. A similar argument could be made for bracelets, which, if worn around the wrist, arm or ankle, would need to adhere to regular arm or leg dimensions. The same applies to sleeve-fasteners: if these objects really were used to fasten clothing, there is only so much variation possible, as the objects would quickly become too small or too large to be effective. In short, although mass-regulation may appear evident in certain objects, it is possible that regulation was based on a different characteristic that becomes visible through the mass values.
There can be little doubt that gold objects were valued both intrinsically and emotionally by their owners. A general mass-regulation amongst gold objects would suggest that the metal had a broadly recognised material value and played a part in economic transactions, as has been demonstrated for silver and copper, and suggested for Mycenaean (Ialongo et al. Reference Ialongo, Vacca and Peyronel2018; Ialongo & Rahmstorf Reference Ialongo, Rahmstorf, Rahmstorf and Stratford2019; Zurbach Reference Zurbach, Rahmstorf, Barjamovic and Ialongo2021) and British Bronze Age (e.g. Rahmstorf Reference Rahmstorf2019: 1207) gold. As with silver and copper, the mass-regulation of gold would have followed the same metrological pattern as balance weights. Although there are strong indications that weighing was present in Britain from at least the Middle Bronze Age, the evidence for balance weights themselves is poor (Rahmstorf Reference Rahmstorf2019: 1199–1202). Moreover, the mass ranges proposed by Rahmstorf (Reference Rahmstorf2019: 1203) do not appear to match any known Western European metrological system (see Ialongo & Rahmstorf Reference Ialongo, Rahmstorf, Rahmstorf and Stratford2019). Although gold could have been used in transactions—negotiated on an individual basis—the lack of regulation and compliance with weight systems makes it unlikely that gold was used as currency or as a reference material for value ratios.
Conclusion
This study has collected and analysed most of the mass values of known British Bronze Age gold objects, with results showing that a general mass-regulation could not be identified for any of the object classes. This stands in contrast to previous studies on the subject. Supplementing Rahmstorf's (Reference Rahmstorf2019) dataset demonstrates the importance of reanalysis as new data emerge and new material is discovered. It is possible that, with sufficiently large quantities of new evidence, the results may change our interpretations yet again. For now, it seems that gold objects in Bronze Age Britain were not regulated by mass.
Acknowledgements
I would like to thank the curators and owners of material who have provided information about their collections, Nicola Ialongo and Lorenz Rahmstorf for discussions and Laura Hermann for help with the text. All opinions and errors are my own.
Funding statement
This work was supported by the European Research Council under the European Union's Horizon 2020 Framework Programme, and was carried out within the scope of the ERC-2014-CoG ‘WEIGHTANDVALUE: Weight Metrology and its Economic and Social Impact on Bronze Age Europe, West and South Asia’, based at Georg-August-Universität, Göttingen, Germany [grant 48055]; Principal Investigator: Lorenz Rahmstorf.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.15184/aqy.2021.54