Use of a snowmelt model for weekly flood forecast for a major reservoir in Lithuania

Abstract

A snowmelt model is used for the weekly forecast of daily discharges in the Kaunas reservoir, Lithuania. The results are used to feed a risk-based decision-making model developed by the first author for dam operation during floods. Physically based calibration of a degree-day model is carried out and coupled with flow routing using Nash’s instantaneous unit hydrograph theory. Temperature forecast is used as the driving variable. Due to the relative smoothness of snowmelt over time and the considerable basin size, the model provides acceptable results. Kalman filtering is then used to merge the estimates from the snowmelt model with those from an Arima flow model, resulting in better forecasting than that using each method alone. Uncertainty analysis of the snowmelt-model results is then carried out, showing considerable influence of the main parameter degree-day and of soil moisture conditions. Therefore these must be accurately estimated for forecasting purposes during flood events.

1. Introduction

On 18 January 2006 the European Commission proposed a directive aiming to reduce the impact of flooding upon human health, the environment and infrastructure. Under the proposed directive, the member states would first need to carry out a preliminary assessment to identify the river basins and associated coastal areas at risk of flooding. A keystone for risk evaluation and management in hydropower plants is flood forecasting. The largest Lithuanian hydropower system consists of the Kaunas hydropower plant and the Kruonis hydro-pump storage power plant, both taking water from the Kaunas reservoir, located on the longest Lithuanian river, the Nemunas. This is a transnational basin, covering 97 928 km² in four countries, Lithuania, Belarus, Poland and Russia (Kaliningrad district), and flowing into the Curonian lagoon (Lithuanian part of the Baltic Sea). The main functions of the reservoir are flood control and hydropower generation, but also recreation, water transportation and fishing. The biggest floods in the Nemunas river originate from snowmelt, usually occurring in early spring. Usually the temperature rises abruptly, with waterproof frozen soil to a depth of 40– 50 cm and sometimes even as deep as 100 cm, resulting in rapid snowmelt and runoff therein. The first author developed a risk-based decision-making model for the Kaunas hydropower system, requiring the forecast of the incoming daily discharges with a lead time up to 7 days (Simaityte and others, 2006). A model, herein named D-IUH, is presently being developed to account for snowmelt, which was not incorporated in the statistical approaches for flood forecasting. A degree-day model is calibrated and coupled with flow routing via Nash’s instantaneous unit hydrograph (IUH) theory. The temperature forecast is used as a driving variable to feed the degree-day model. Data fusion based on a Kalman filter can be carried out with a standard autoregressive integrated moving average (ARIMA) model. This allows improved forecast of flow discharges. Uncertainty analysis is then carried out for different lead times from 1 day to 1 week, to specify the parameters that require more accurate estimation.

2. Case Study

The Kaunas reservoir system is sketched in Figure 1. The Kaunas reservoir takes water from the Nemunas river basin, covering an area of 45 800 km² in Lithuania and Belarus.

Fig. 1. Kaunas hydropower system.

The average annual flow in the Nemunas at Kaunas is 287 m³ s^–1. The average flooding period in the Nemunas river ranges from 6 March to 9 May, with greatest flows between 24 and 30 March. The river daily flow database for the period 1920–2001 was investigated, and showed that the greatest floods occur in spring, requiring in practice the analysis of spring data for flood forecasting. The annual flood series (AFS), i.e. the series of the greatest annual floods, showed a mean value of 953 m³ s^–1, with the biggest flood in 1958, when a peak of 3450 m³ s^–1 was observed on 24 April. Other relevant events are 2060 m³ s^–1 in 1979, and 2330 m³ s^–1 in 1931. Another 30 events with peaks over 1000 m³ s^–1 were also observed.

The flood-forecasting system presented here is based on a general scheme as given in Figure 2.

Fig. 2. The Nemunas river real-time flood forecast scheme.

3. Methodology

3.1. D-IUH runoff model

A runoff model was developed based on the degree-day and IUH (see, e.g., Chow and others, 1988). The degree-day approach is designed to simulate and forecast daily flow in mountain basins where snowmelt is a major runoff factor (e.g. the snowmelt-runoff model (SRM; Martinec, 1975)). However, with respect to the typical degree-day approach, here a more refined description of the watershed dynamics is introduced using the IUH technique. Remotely sensed imagery is typically used to evaluate the snow-covered area (e.g. Martinec, 1975) for the SRM. Because the greatest observed flood events used here date back to the period 1958–79, no remotely sensed imagery was available (the 26 greatest events occurred before 1990; the highest peak thereafter, occurring in 1994, was 1070 m³ s^–1). It was therefore assumed that the river basin was homogeneously covered in snow during snowmelt. This is reasonable because the watershed presents a flat aspect. Snow-cover conditions are assessed here using snowpack data from gauging stations. The most important input in the SRM is the depth of meltwater in a given day n, i.e. snow water equivalent (SWE), which is expressed as:

(1)

with a a degree-day factor, indicating the snowmelt depth resulting from 1 degree-day (cm ^˚C^–1 d^–1), T_n the mean daily air temperature (^˚C) and T ₀ the threshold air temperature for snowmelt (here set to 0^˚C based on snow data analysis). In general, the value of the degree-day factor varies during the melt period because of changes in the snow properties, which influence the melting process and should therefore be estimated from the observed snow data. However, here a constant value of a was found to represent the snowmelt process well.

The IUH is defined as the direct runoff hydrograph resulting from a unit volume of excess rainfall of constant intensity and uniformly distributed over the drainage area. The present model calculates the net snowmelt equivalent using the Soil Conservation Service curve number (SCS-CN;

e.g. Gupta, 2001):

(2)

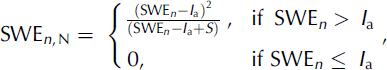
where SWE _{n, N} is the the net snowmelt depth (mm), I _a = cS is the initial abstraction, with c as a calibration coefficient (here 0.2) and S = 254(100/CN – 1) the maximum specific volume that can be stored in the ground, and CN a curve number representing soil permeability. In this case, the Nash model (see, e.g., Chow and others, 1988) was used for IUH evaluation, which is expressed as a two-parameter gamma distribution function:

(3)

with β a shape parameter, k a scale parameter and Γ(β) the complete gamma function.

Then, considering the IUH as the response of a linear system to an instantaneous impulse of unit volume of precipitation, the flow routing in the basin can be evaluated using the convolution integral:

(4)

with u(t) the instantaneous unit hydrograph and τ a dummy variable used for integration. Having the estimated flow-routing values, the daily flood discharge Qˆ(t) (m³ s^–1) is calculated as:

(5)

with A the drainage area (km²) and Q ₀(t) the base flow (m³ s^–1). Base-flow estimation was performed here using the separation by recession curve approach (see, e.g., Furey and Gupta, 2001).

3.2. ARIMA model for temperature and flow

Linear stochastic processes are among the most widely used time-series techniques for modelling water resources. Here an ARIMA(p,d,q) model (e.g. Box and Jenkins, 1976) is used:

(6)

with x_t a zero-mean time-series, η_t the white noise, Ф and Θ respectively the pth- and qth-order auto-regressive and moving-average components, B a backward shift operator defined so that B^jx_t = x_t ^– j , and d the order of differentiation of the original data, i.e. the minimum non-negative integer necessary to obtain a stationary process by differencing the original series. Forecasting of the flow or temperature values

for 1,2,. . .,n days is performed going step by step ahead using the ARIMA model with estimated parameters using all available data.

4. Model Application

4.1. Database

Here three events showing relatively good documentation were selected from the AFS. Two of these, for the years 1958 and 1979, are the largest and third-largest events ever observed (no database was available for the second-largest event, dating back to 1931, with an estimated peak flow of 2330m³ s^–1). Temperature data were available from five measuring stations in Belarus and one in Lithuania, while daily precipitation data were available from seven stations in Belarus and one in Lithuania. Winter snow precipitation and daily snowpack data (depth and mass density) were available from two Lithuanian measuring stations.

4.2. D-IUH model estimation

The D-IUH model was calibrated for the 1979 flood event and validated for the events in 1970 and 1958. The 1979 event (Fig. 3) is used for calibration because it shows the most complete database. A constant degree-day factor was estimated by regression of cumulated melted snow from snowpack data against the daily temperature series, resulting in a = 0.23 cm d^{–1 ˚}C^–1. Using this value and knowing the initial snow depth on the ground, i.e. the greatest available amount of water SWE_max, the melted snow amount can be back-estimated from daily temperatures (in Fig. 3). The CN value is estimated by equating the net snowmelt volume with the runoff volume (total volume minus base flow volume). For the 1979 event, CN = 68. Nash’s model parameters β and k were calibrated by a least-squares error approach as:

Fig. 3. Year 1979. D-IUH model calibration: calculated and observed daily flow and snowmelt.

with ε the error in flow discharge prediction from the model. For every flood event the mean average percentage error (MAPE) rate was used to check flow simulation and forecast accuracy:

with n the number of flood days, q_i the observed discharge

values and p_i the modeled discharge values. A forecast is usually considered to be very good for MAPE < 10%, good for MAPE < 20% and acceptable for MAPE < 50%. The MAPEs for flow simulation (i.e. with known model inputs; no forecasting) for 1979, 1970 and 1958 are given in Table 1. Figure 3 presents the results of the D-IUH calibration. Notice the reasonable accuracy (1 day ahead) in defining the snowmelt period, i.e. the day of snow depletion, and the resulting accuracy of the flood peak date. Validation for 1970 and 1958 was carried out by taking the same a, β and k values as in 1979. In this case, no snowpack data were available. However, cumulative snow-depth precipitation was available during the accumulation season. This was used to set an initial condition for SWE_max. Again, for 1958 and 1978, the simulated ablation dates coincided fairly well with the observed flow-peaking dates, indirectly witnessing the likelihood of the a values. The CN had to be changed; otherwise the model yielded unreasonable flow rates. This was expected, because CN is variable from event to event, requiring direct evaluation in practice (e.g. Bocchiola and Rosso, 2006a). However, after the CN was tuned, the D-IUH model performed reasonably well.

Table 1. D-IUH model. Calibration for 1979 and validation for 1970 and 1958. Italic indicates parameters set a priori for validation. ‘Rank’ is position of q _peak in the AFS. T is the relative sample return period

4.3. Arima model estimation

For short-term temperature forecasting, an ARIMA model was chosen, and its parameters evaluated using winter–spring daily temperature values. The temperature series were divided by standard deviation and detrended, i.e. the linear increasing trend of daily temperature during the flood event period was subtracted from data. Preliminary tests showed that, for a given daily temperature series, the optimal forecasting performance (i.e. least forecast error) was given by an ARIMA(1,1,1) model. Notice that here temperature forecasting was accomplished using simple ARIMA modelling techniques, in view of the simple dataset that was available for 1979. More refined sources are now available (e.g. 7 day temperature forecast from meteorological cen-tres). An ARIMA model was also applied to flow discharges (e.g. Montanari and others, 2000). Optimal performance was obtained using an ARIMA(2,2,2) model. The model was then applied for flow forecasting (Fig. 4).

Fig. 4. Year 1979. Flood forecast of the peak disharges for LT = 1–7 days. D-IUH and ARIMA models and new estimates using Kalman filter.

4.4. Flood forecasting with D-IUH model

The flood forecasting was performed using temperature as a driving variable to feed the D-IUH model. The temperature forecast was simulated using the ARIMA model, and the result was then used for snowmelt estimation in Equation (1). Using Equations (2–5), the flood forecast could then be carried out for lead times L_T from 1 to 7 days. Here, only forecasting of the 1979 event was considered, because it includes a more complete database. Issuing of a forecast according to the risk-based decision-making procedure starts after an attention level is reached, fixed at 500 m³ s^–1. An example of forecasting for L_T = 7 days is presented in Figure 4. The forecasts from 1 to 7 days ahead are shown, issued on 4 April, close to the peak date. MAPE for forecast ranges from 4.9% for L_T = 1 day to 7.6% for L_T = 7 days, reported in Table 2. This seems reasonable, because the D-IUH model was properly calibrated a posteriori.

Table 2. 1979 event. Accuracy in flood forecast based on MAPE (%). Lead time 1–7 days

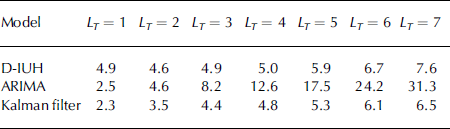
4.5. Flood forecasting with Kalman filtering

The D-IUH model shows a memory on the order of the lag time, here T _l = βk = 7.8 days. The ARIMA model is instead a shorter-memory model, as it uses a few of the last flood measurements, thus being decreasingly effective for longer-duration flood forecasts. It seems warranted that the greatest possible amount of information is gathered by data fusion of the forecasts from the two models.

Kalman filtering is a reliable tool for data fusion and forecasting (Bocchiola and Rosso, 2006b; Bocchiola, 2007) and provides an optimal (i.e. unbiased and least-variance) estimation. The equations for Kalman filtering are widely known (e.g. Bras and Rodríguez-Iturbe, 1985), so are not reported here. Kalman filtering was carried out using the ARIMA as the state variable model, and the D-IUH forecasts as surrogates for noisy measurements. The variance of estimation of D-IUH is the sample variance of the forecast error by the D-IUH model alone. In Figure 4, the flood forecast for 1–7 days ahead as obtained by the Kalman filter is shown.

Clearly a poor forecast is obtained using the ARIMA model after about 3 days, while the D-IUH model results in more accurate forecasts until approximately day 5. However, after a longer period, i.e. for days 6 and 7, the performance of the D-IUH model seems to decrease. The Kalman filter seems to improve the accuracy of either model used independently. Similar results were observed for most of the cases, when issuing a 7 day forecast starting from different dates. The full results of the comparison in term of MAPE are given in Table 2.

5. Uncertainty Analysis

Uncertainty analysis of the decision-making procedure indicates that the input parameters of the flood-forecasting model are a main source of uncertainty (e.g. Augutis and others, 2004). Therefore, an analysis was performed on the D-IUH model to determine the main source of uncertainties in the forecast. This evaluation is necessary to specify the most important parameters, i.e. those that need to be evaluated online for a better flood forecast exercise. Uncertainty of the D-IUH forecasts arises because the main parameters (i.e. a, CN, β and k) are not known a priori and can vary between different events. To carry out an uncertainty analysis for a number of parameters, x ₁, x ₂ . . . x_n , one can model them as random variables with given probabilistic density functions p(x₁), p(x₂) . . . p(x_n ).

When uncertainty is due to measurement errors, a normal distribution is usually reasonably valid; other distributions that can also be used are triangular, uniform, log-normal and beta. In this case, normal and triangular distributions were selected after a preliminary analysis (omitted for brevity; see Table 3).

Table 3. Probabilistic distributions of D-IUH model parameters

To test the sensitivity of the D-IUH to the input values of the parameters, 93 numerical simulations were carried out using SUSA1 software. According to Wilks (1942), this is the lowest number of simulations required for assessment of the 95% confidence limits to the flow forecast. Random values of the parameters were extracted according to the defined distributions and then fed to the D-IUH used for forecasting. The 1979 flood event was considered. The analysis provided a flood forecast for L_T = 7 days, presented in Figure 5 for an interval close to the peak.

Fig. 5. Year 1979. Uncertainty analysis of flood forecast for LT = 7 days. Various model runs with parameters selected from distributions in Table 3 are compared to the measured hydrograph.

Analysis of the forecast results against the set of input parameters resulted in a determination coefficient R ² = 0.80. This means that uncertainty in the forecast model is reasonably well explained by the variability of the model parameters. Sensitivity analysis to input parameters was then performed using Spearman’s correlation coefficient S _cc (–1≤S _cc≤1) which shows the contribution to uncertainty resulting from each parameter in the model. Estimation of S _cc is presented in Figure 6. The greatest value of S _cc is associated with the degree-day factor a (from S _cc = 0.69 for L_T = 1 to S _cc = 0.78 for L_T = 7). The slight decrease of S _cc for CN as L_T increases is likely explained by an increase of soil saturation during flood. The Nash parameters β and k are negatively correlated and S _cc is less than 0.3 in absolute value.

Fig. 6. Year 1979. S _cc of D-IUH model parameters.

As such, the conclusion can be drawn that the greatest uncertainty is brought about by the degree-day factor a. Consequently, accurate estimates of a must be carried out, particularly when a flood event starts, to achieve accurate online calibration of the D-IUH model. Care is also required in setting CN to accurately forecast the flood volume.

6. Conclusions

Hydrological modelling based on a degree-day snowmelt model and IUH theory was developed and applied to the Nemunas river to forecast daily flow at the Kaunas reservoir. The D-IUH model was calibrated for a case-study event in 1979 and validated for two events in 1970 and 1958, showing good capability to represent the flood phenomena. For the 1979 event, a temperature forecast from an ARIMA model was fed to the D-IUH model, obtaining an acceptable flood forecast for lead times up to 1 week. To improve the model performance, the forecast from an ARIMA model for flood discharges was merged with that from the D-IUH using a Kalman filter, resulting in increased accuracy. Uncertainty analysis of the D-IUH model displayed considerable influence of the degree-day factor and soil moisture via the curve number CN. Therefore, online updating of these parameters can lead to increased forecast accuracy. Forecasting of flood events nowadays can profit from more comprehensive meteorological forecasts, resulting in more accurate temperature assessments, rather than ARIMA temperature forecasts. Also, the use of remotely sensed imagery can result in more accurate snow-cover estimation for the D-IUH model.