Site-specific analog weather-forecast system for northwest Himalaya, India

Abstract

In an analog weather-forecasting procedure, recorded weather in the past analogs corresponding to the current weather situation is used to predict future weather. Consistent with the procedure, a theoretical framework is developed to predict weather at a specific site in the Pir Panjal range of the northwest Himalaya, India, using surface weather observations of the past ten winters (1991/92 to 2001/02) 3 days in advance. Weather predictions were made as snow day with quantitative snowfall category or no-snow day, for day1 through day3. As currently deployed, the procedure routinely provides a 3 day point weather forecast as guidance information to a weather and avalanche forecaster. Forecasts by analog model are evaluated by the various accuracy measures achieved for an independent dataset of three winters (2002/03 to 2004/05). The results indicate that weather forecasts by analog model are quite reliable, in that forecast accuracy corresponds closely to the relative frequencies of observed weather events. Moreover, qualitative weather (snow day or no-snow day) and quantitative categorical snowfall forecasts (quantitative snowfall category for snow day) are better than reference forecasts based on persistence and climatology for day1 predictions. Site-specific snowfall forecast guidance may play a major role in assessing avalanche danger, and accordingly formulating an avalanche forecast for a given area in advance.

Introduction

That analogs can be used for forecasting future weather is a very old idea. Analog forecasting (AF) consists of searching for analogs to the present or preceding situation and then predicting weather for the forthcoming period. The main advantages of its use are that it yields a real solution to a difficult problem (Namias, 1951, 1968), is adaptable to microclimatological influences of the forecast area and requires far less expenditure of resources (human and computational) than currently available numerical weather-prediction models (NWPs).

Many previous studies have been made of the possibility of weather prediction using the AF procedure on a large spatial scale with large-scale flow pattern. The results obtained by Lorenz (1969), Gutzler and Shukla (1984) and Ruosteenoja (1988) were disappointing for short- and medium-range weather forecasting using the AF procedure in both time and space with large-scale flow pattern. However, AF procedure has shown considerable capability in the long-range prediction of weather and its various elements (Barnett and Preisendorfer, 1978; Kruizinga and Murphy, 1983; Toth, 1989).

A limited-area AF model approach for short-range weather forecasting using 500 mbar height analyses was proposed by Van den Dool (1989). The results of short-range limited-area point AF procedure were in marked contrast to those of earlier studies (Lorenz, 1969; Gutzler and Shukla, 1984; Ruosteenoja, 1988), and were encouraging.

In this paper, we study the predictability of weather (snow day with quantitative snowfall category or no-snow day) at a specific site (Stage II (2650ma.s.l.); Fig. 1) in the Pir Panjal range of the northwest Himalaya (NW-Himalaya) employing AF procedure using surface weather parameters (see ix A) during the winter period (November–April). Surface weather parameters are used in this study for several practical reasons: First, they provide weather-forecast guidance to a weather or avalanche forecaster who has a limited source of data in a remote area of NW-Himalaya. Second, NWP guidance with the help of a regional mesoscale weather simulation model, MM 5 (Srinivasan and others, 2004; A. Singh and others, 2005), is possible with at least a 24 hour time lag (NWP guidance is available with the data at least 24 hours earlier than the forecast time) due to the real-time unavailability of data for initialization of the MM 5 model. Third, it is difficult to simulate/predict surface weather elements such as temperature and precipitation over complex mountainous terrain with the help of NWP models (Mohanty and Dimri, 2004).

Fig. 1. Chowkibal Tangdhar axis in the Pir Panjal range of NW-Himalaya, India.

An analog model is developed using surface weather observations of a specific site, and forecasts produced by the AF model are verified at that site. This is mainly due to large variability in weather and its various elements such as temperature and precipitation over NW-Himalaya. This variability can be attributed to the high dependency of surface weather elements upon local topography and local atmospheric circulations over NW-Himalaya. The purpose of developing an area-specific analog weather-forecast model is to capture the effect of local topography on the weather and precipitation pattern over the area from the past database of surface weather observations of the area, and partially to fulfill the requirement of area-specific weather-forecast guidance for operational avalanche forecasting during winter. Weather forecasts assume primary importance during winter in NW-Himalaya because solid precipitation (snow) affects large sectors of the economy (transportation, construction, agriculture, commerce). Snowfall forecast is important not only from the operational weather-forecasting point of view, but also for avalanche forecasting (Perla, 1970; LaChapelle, 1980). Weather-forecast guidance at a specific site during winter can help the avalanche forecaster to assess avalanche danger and thus formulate the avalanche forecast for a given area.

The diversity of interactions between large-scale weather phenomena and the local topography and their outcome (weather or precipitation pattern) remain implicitly preserved in the past database of surface weather observations of any area. Therefore, surface weather observations can be used to predict weather over an area. Thus, our first effort is to establish a theoretical framework and evaluate the potential of the AF procedure as a means of predicting weather at a specific site using surface weather parameters.

At present, AF procedure is made to predict weather in the same fashion as predicted with the help of currently available NWP models (snow day with snowfall amount or no-snow day). This seems reasonable until the AF procedure or any other weather-forecasting method can be made credible enough to predict weather as practised (generally preferred) for operational weather forecasting (fair weather; cloudy weather; overcast sky). However, we envision that the AF procedure can be made to provide objective weather-forecast guidance in operational weather-forecasting mode.

The developed analog model is tested with an independent dataset of three winters, and weather forecasts produced by the model are compared with the standard reference forecasts based on persistence (hereafter persistence forecast) and climatology (hereafter climatological forecast) for day1 predictions. The climatological forecast of the day under consideration is the mean snowfall recorded on the same day (Julian day) in past years of the dataset. It is a constant forecast for all three days for the independent dataset. A persistence forecast for day1 consists of the recorded snowfall 1 day before the day in question (e.g. today). Persistence forecasts produced on this basis for day2 and day3 may lead to very inaccurate predictions. Therefore, only the persistence forecast for day1 is considered.

The results of this study indicate that reasonable forecast accuracy is possible for weather at a specific site using AF procedure with surface weather parameters. Weather forecasts produced by the analog model are better than forecasts based on persistence and climatology for day1 predictions at a specific site.

Study Area and Data used

The present study area falls in the Pir Panjal range of NW-Himalaya. Surface weather observations taken for the development of an analog model belong to the Stage II observatory situated on a highway connecting the Chowkibal valley with Tangdhar at Nasta-Chung Pass at 3120 ma.s.l. This 40 km stretch of highway has 26 registered avalanche sites, which affects movement along the highway. Snow, meteorological and avalanche occurrence data are regularly collected and monitored at Stage II (Fig. 1) for operational avalanche forecasting and snow-related studies during winter.

Surface weather parameters such as maximum temperature and its deviation in the previous 24 hours and minimum temperature and its deviation in the previous 24 hours (see Appendix A) are used to search analog situations corresponding to the current situation from the past database of surface weather observations of Stage II. Surface weather observations measured manually twice daily at 0300 UTC and 1200 UTC in the past ten winters (winter 1991/92 to winter 2001/02, excluding the missing data of winter 1994/ 95) at Stage II are used to develop the analog model. The model is tested with the independent dataset of three winters (winter 2002/03 to winter 2004/05).

One of the foremost requirements for an analog search process is a complete dataset, i.e. all the parameters are available for all the days. Unfortunately, our dataset is not complete (one or more parameters may be missing during winter due to sudden instrument failure). Replacement or repair of the instrument could not be undertaken due to the remoteness of the location and the hazardous winter conditions. The parameters are kept intact and analog situations are searched with the missing parameter.

An Analog Search Procedure and Model Development

The analog situations are sought here by calculating the Euclidean distance, given below, between the current-day surface weather observations (x_ik ) and the surface weather observations of the candidate analogs (x_jk ) (Barnett and Preisendorfer, 1978; Toth, 1989; Van den Dool, 1989). The analog situations for any day are searched from the past dataset, where the date lies within ±30 Julian days of the day under consideration (Van den Dool, 1989).

With x_k as the vector of k measurements for day i,

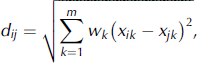
where d_ij is the distance between day x _i and x _j , and w _k is the weight assigned to the kth parameter. Assigning weights to the different parameters gives relative importance to them for searching an analog situation and is considered an expert task (Buser, 1983). The weights assigned to the different parameters are given in Appendix A. These weights are assigned based on general experience of surface weather observations and observed weather at the forecast site in the past. For example, surface atmospheric pressure at the reference station is assigned maximum weight, because the drop in atmospheric pressure at the reference station is an indirect indication of the approach of westerly disturbance (bad weather over the area).

In the case of a perfect match, the Euclidean distance is zero, and smaller values of Euclidean distance indicate better analogs (Kruizinga and Murphy, 1983; Van den Dool, 1989). In the scan of the historical dataset, the date and snowfall recorded in the next 24 hours of ten analogs (ten lowest distance values) are retained. These ten analogs represent weather observed in the past under similar conditions of surface weather observations at a given time (e.g. today).

In addition to the ten best analogs, the preceding situation and two successive situations corresponding to each analog situation are also searched from the past database. The preceding and two successive situations represent the state of weather at the previous measurement time and at two successive measurement times corresponding to analogs. The date and snowfall recorded in the next 24 hours corresponding to the preceding and two successive situations are retained along with the analog situations. It may be expected that the weather events will be similar, as reported in the past for successive situations under the similar conditions of surface weather parameters at the same geographic location. Therefore, analog situations are assumed to be representative of the state of the weather for day1 (next 24 hours), and two successive situations are assumed to be representative of the state of the weather for day2 (next 24–48 hours) and day3 (next 48–72 hours) for the development of an analog model. With this assumption, the probability of snowfall for day1, day2 and day3 is calculated from the searched analog, preceding and succeeding situations using the following expression (Singh and Ganju, 2004):

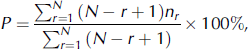
where N is the number of analog situations (10 in the present case), r is the rank of an analog situation (1–10 in the present case) and n_r is 1.0 if the rth analog situation is the snow day, otherwise 0.0.

For calculating the probability of snowfall using the above expression, analog situations are ranked according to their nearness to the current situation (first analog situation is given maximum weight and tenth analog situation is given least weight).

While predicting weather for three consecutive days, it is necessary to consider the preceding situations (Singh and Ganju, 2006). This has been achieved by taking the weighted average of probability of snowfall for that day and that of the previous day (while forecasting for day2, the weighted average of probability of snowfall for day1 and day2 is taken (Singh and Ganju, 2006)). Thus, the decision criterion of the AF system is defined as

where P_n is the probability of snowfall for the day under consideration and P_n –₁ is the probability of snowfall for the previous day. The AF system based on the value of D (>40) produces a qualitative categorical weather forecast (snow day or no-snow day).

Once any day is predicted as a snow day, the AF system based upon the mean snowfall associated with the analogs predicts the snowfall amount for day1 using the following expression (D. Singh and others, 2005):

where X̄ is the mean snowfall in the analogs and X_i is the snowfall recorded in the ith analog.

The quantitative snowfall amount for day2 and day3 is predicted based on mean snowfall in the successive situations using the above expression. The quantitative snowfall amount reported in the preceding and successive situations is not considered to predict snowfall amount for any day. This is mainly due to the consideration that snowfall amount on the day following any day may not depend on previous days’ snowfall amount (e.g. heavy snowfall is less likely after heavy snowfall on the previous day).

The quantitative snowfall predicted for snow day by the AF system is changed into a quantitative snowfall category, one among the set of six disjoint snowfall categories (Table 1), as practised for operational weather forecasting in NW-Himalaya (Snow and Avalanche Study Establishment weather-forecast report). The quantitative snowfall category is assigned to any snow day to which predicted snowfall amount belongs.

Table 1. Quantitative snowfall-forecast categories practised for operational weather forecasting in NW-Himalaya and their occurrence statistics at Stage II

The developed AF system is tested and evaluated for the prediction of a qualitative categorical weather forecast (snow day or no-snow day) and quantitative categorical snowfall forecast (quantitative snowfall category for snow day). These two schemes are adopted intentionally to find out whether the AF system is capable of predicting snow day, since snow-day prediction can be considered equivalent to rare-event prediction, given the predominance of no-snow days (74% of days of test data). Thus, qualitative categorical weather forecasts are of primary concern, and particular emphasis is placed on various statistical accuracy measures achieved. The performance of AF procedure for a qualitative categorical weather forecast may directly indicate the utility of AF procedure for forecasting weather. The failure of AF procedure for a qualitative categorical weather forecast will directly imply its failure for quantitative categorical snowfall prediction.

Weather forecasts based on climatology and persistence are also changed into qualitative categorical weather and quantitative categorical snowfall forecasts. For this purpose, any day predicted with snowfall amount ≥1.0 cm (best accuracy of snowfall measurements in the past database) by persistence and climatological forecasts is taken as a snow day, and otherwise a no-snow day, and quantitative snowfall category is assigned to any snow day to which the predicted snowfall amount belongs. This ensures proper comparison of forecasts by the AF system, with the forecasts based on persistence and climatology.

Results

Weather forecasts by persistence, climatology and AF model for 544 days of test winters are verified at Stage II. Statistical accuracy measures considered for evaluation of qualitative categorical weather forecasts are probability of detection (POD), miss rate (MR), false alarm rate (FAR), correct non-occurrence (C-NON), critical success index (CSI) and percent correct (PC) (Wilks, 1995; Mohanty and Dimri, 2004), and are given in Appendix B. The bias (BIAS) is used as a measure of over-forecast or under-forecast tendency of all three forecast methods.

The accuracy of each method of forecasting quantitative categorical snowfall is defined as the percentage of snowfall category observed in the predicted snowfall category. The forecast accuracy for quantitative categorical snowfall forecast may not represent the quality of quantitative categorical snowfall forecast produced by each forecast method. Therefore, quantitative categorical snowfall forecast error is considered: the percentage of snowfall categories recorded outside ±1 category of predicted snowfall categories, for each forecast method. Accurate and precise prediction of snowfall amount is an extremely difficult and challenging task (Charba and Klein, 1980; Roebber and others, 2003, 2004). Therefore, more than one category distant observation of any predicted snowfall category is considered as a quantitative categorical snowfall forecast error. This, however, may give only a broad idea of the quality of the quantitative categorical snowfall forecast produced by each forecast method.

The qualitative weather-prediction performance of persistence and climatological forecasts for day1 and the analog model for all 3 days at a specific site is given in Table 2. The overall accuracy (PC) of the persistence forecast and analog model is comparable and it is poor for climatological forecast compared to that for day1 predictions (Table 2). In our context, the overall accuracy of the qualitative weather prediction cannot be taken as the measure of performance of any forecast method, due to the predominance of no-snow days (Murphy, 1996). Therefore, forecast accuracy measures such as POD, MR, FAR, C-NON and CSI are also considered, in addition to overall accuracy (PC). Significant differences in the POD, MR and CSI of an analog model and the persistent forecast for day1 predictions suggest that the analog model predicts snow days better than does the persistence forecast (Table 2). However, the FAR of the persistence forecast is less than that of the analog model for day1 predictions. This indicates that more no-snow days are predicted as snow days by an analog model compared to the persistence forecast for day1 predictions. Such false predictions are produced by the analog model when significant change in the surface weather parameters is not observed due to prevailing, departing westerly disturbance or when subsequently moving westerly disturbance merges with already existing, yet departing, westerly disturbance over the area. The persistence forecast and the analog model predict no-snow days more accurately than snow days (high value of C-NON compared to POD) for day1 predictions. This can be attributed to the large number of no-snow days (74%, test data) compared to snow days.

Table 2. Accuracy measures of persistence, climatological and analog models for qualitative weather prediction (snow day or no-snow day) at a specific site for independent dataset for past three winters (winter 2002/03 to winter 2004/05)

The POD of the climatological forecast is significantly more than the POD of the analog model and the persistence forecast for day1 predictions. The MR of the climatological forecast is also significantly less than that of the analog model and the persistence forecast for day1 predictions. However, the FAR of the climatological forecast is significantly more than that of the analog model and persistence forecast for day1 predictions. The POD and FAR of the climatological forecast indicates the complex pattern of snowfall events observed in the area. The climatological forecast predicts only 26% of no-snow days correctly, reducing the overall performance of the climatological forecast to 44.1%. The various accuracy measures suggest that the analog model performs best and the climatological forecast worst of the three for qualitative weather prediction for day1 predictions.

Various accuracy measures show that the performance of an analog model decreases with lead time (day 1 through day 3). Decrease in the POD, CSI and PC of the analog model is found more from day1 to day2 predictions than from day2 to day3 predictions. Increase in the FAR and MR is found more from day1 to day2 predictions than from day2 to day3 predictions.

The persistence forecast under-forecasts snow day, and the analog model over-forecasts snow day, slightly more than the unbiased forecast (BIAS = 1.0) for day1 predictions. The under-forecast tendency of the persistence forecast is a more serious issue than the slight over-forecast tendency of the analog model from an operational weather-forecasting point of view. The over-forecast tendency of the climatological forecast is more than twice that of the analog model and more than three times that of the persistence forecast. The over-forecast tendency of the analog model does not increase significantly with the lead time.

Quantitative categorical snowfall forecast by persistence and climatological forecasts for day1 and the analog forecast for all three days is given in Figure 2. Quantitative categorical snowfall-forecast accuracy of the analog model is found to be better than the persistence and climatological forecasts for snowfall forecast categories B, C and D for day1 predictions. However, the analog model does not predict snowfall events which take place rarely in the area (A and E). The overall accuracy (PC) and forecast error of the quantitative categorical snowfall forecast of analog, persistence and climatological forecasts is given in Figure 3. The analog model shows significantly better overall accuracy than the persistence and climatological forecasts (Fig. 3) for day1 predictions. The quantitative categorical snowfall-forecast error of the analog model is also found to be less than that of the persistence and climatological forecasts for day1 predictions. This suggests that the analog model performs the best of the three for quantitative categorical snowfall forecast for day1 predictions (Fig. 3). The climatological forecast is least accurate, with the maximum forecast error for quantitative categorical snowfall-forecast for day1 predictions. The overall performance of the analog model decreases for quantitative categorical snowfall prediction as the lead time of the forecast increases (Fig. 3). However, quantitative categorical snowfall-forecast error of the analog model does not increase significantly with lead time (day1 through day3).

Fig. 2. Quantitative categorical snowfall prediction by persistence, climatological and analog models.

Fig. 3. Quantitative categorical snowfall-forecast accuracy and error of persistence, climatological and analog models.

The analog model performs best of the three for qualitative weather and quantitative categorical snowfall forecast for day1 predictions. Its performance decreases for day2 and day3 predictions for qualitative weather forecast. However, its overall performance for quantitative categorical snowfall forecast does not decrease significantly, and quantitative categorical snowfall forecast error does not increase significantly, as the lead time of forecast increases (Fig. 3). This is interesting from an avalanche-forecasting point of view. Site-specific snowfall forecast guidance by an analog model may help the avalanche forecaster to assess avalanche danger and accordingly to formulate avalanche forecast for the area. However, at present, quantitative snowfall forecast guidance provided by an analog model is not tied to any avalanche prediction model. This is because avalanche forecasting also requires predicted values of other meteorological parameters such as temperature and wind, along with the predicted snowfall amount. Therefore, predictions made with the help of an analog model may help in formulating avalanche forecast in view of weather-forecast guidance for the area.

Discussion and Conclusions

We have described some results of a study in which an AF procedure is employed for weather prediction for three consecutive days at a specific site in NW-Himalaya. Both qualitative weather and quantitative categorical snowfall forecasts are derived from the distribution of snowfall events associated with analog, preceding and successive situations. Attention was primarily focused on the possibility of weather prediction at a specific site using surface weather parameters. In spite of an incomplete and small dataset, the results obtained are encouraging, realizing the complexities of weather prediction and snowfall amount at a specific site in the complex mountainous terrain of NW-Himalaya.

The presented AF procedure provides evidence that a relatively simple empirical method can serve as an independent objective weather-forecasting guidance tool at relatively very low cost. The main conclusions of this study are

• The limited work reported here indicates that the analog method may be a useful weather-forecast guidance tool for a short-range and limited area. However, our short-term and incomplete data (ten winters) have been a severe restriction on the testing of the method. It appears that the method will work better with a long and complete dataset. Therefore, more emphasis is needed on the collection of complete data.

• Comparison of the analog forecast with persistence and climatological forecasts indicates that AF procedure performs better than persistence and climatological forecasts for short-range weather prediction. However, a decrease in model performance for snow-day prediction and an increase in false-alarm rate become the main concern as the lead time of the forecast increases. This may be due to consideration being limited to surface weather parameters, and lack of inclusion of the data taking into account the movement of westerly disturbance. Comparative study of an analog model with the currently available NWP models may be more useful for assessing the potential of an analog model for weather prediction 1–3 days in advance over a limited area. Such a study may reveal some fruitful results for the development of an ensemble forecast scheme.

• The system is portable and is not tied to any NWP model. It may be useful for predicting weather at a specific site with far fewer resources than is the case with currently available NWP models. It is also possible to generate weather forecasts in operational weather-forecasting mode (fair weather, overcast sky, etc.), maintaining consistency between model output and the operational weather forecast.

• The method uses atmosphere as its own model and significantly differs from the perfect prognostic method (Klein and others, 1959) and model output statistics (Glahn and Lowry, 1972).

• In operational forecasting, new forecasts may be required at any time of day as new information arrives from the forecast site. As the interval between the initial time of the NWP model and the current time at which the forecast is needed increases, the NWP guidance may become outdated and new information from the forecast site will be more important for better and accurate prediction. Such requirements can easily be handled with the help of the AF model. Non-availability of data for initialization of the NWP model on a real-time basis (Roebber and others, 2004) can hamper the operational forecasting process based on NWP models.

• The output of area-specific AF models can be integrated to produce a large-scale weather forecast, if needed, such as a regional mesoscale weather forecast. Such models are naturally adapted to trend and system dynamics, are intuitive in nature and can take care of local-scale atmospheric processes.

The demand for accurate weather forecasting at given locations is increasing day by day, due to various socioeconomic developments. It is possible that simple empirical weather-forecast methods can fulfill this requirement to some extent at a low cost. Therefore, there is a need to explore more possibilities in this area.