Simple relations for the close-off depth and age in dry-snow densification

Abstract

A physical model for the snow/firn densification process (Salamatin and others, 2006) and Martinerie and others’ (1992, 1994) correlation for the firn density at the pore closure are employed to perform a scale analysis and computational experiments in order to deduce simplified relations for the close-off depth and ice age in quasi-stationary ice formation conditions. The critical snow density at which ice-grain rearrangement stops is used to take into account variability of snow structures subjected to densification. The results obtained are validated on a representative set of ice-core data from 22 sites which covers wide ranges of present-day temperatures and ice accumulation rates. A simple analytical approximation for the density–depth profile is proposed.

List of Symbols

List of Symbols

Introduction

The transformation of dry snow into bubbly ice, being a fundamental glaciological phenomenon, is also a key process that links paleoclimatic records of ice properties in glaciers to those of atmospheric gases trapped in the ice (e.g. Schwander, 1989; Barnola and others, 1991; Schwander and others, 1997; Goujon and others, 2003; Blunier and others, 2004). From this point of view, the most important general characteristics of the snow/firn densification process are the age t _c of ice at the pore closure and the close-off depth h _c at which all pores become closed and firn transforms to bubbly ice with the close-off relative density ρ _c.

As a continuation of previous studies (Arnaud and others, 1998, 2000), an improved physical model for the snow/firn densification on the ice-sheet surface has recently been developed by Salamatin and others (2006). It has been further constrained and validated by available data (Salamatin and others, in press). Based on Alley’s (1987) and Arzt’s (1982) theories, the model considers the overall vertical (uniaxial) compression of the snow and firn under increasing overburden pressure as a sum of two constituents, one caused by rearrangement of ice grains as rigid particles and another controlled by grain plasticity. In contrast to previous studies, it also takes into account the dilatancy effects in the ice particle repacking. As a result, the first (snow) stage of densification, being dominated by the ice particle rearrangement, is simultaneously influenced by a gradual increase in the dislocation creep of grains. By definition (Arnaud and others, 1998, 2000), the second (firn) stage starts when the grain rearrangement ceases at the closest (dense) packing of ice crystals. Following Arzt (1982), the initial firn structure is described (Salamatin and others, 2006, in press) by the critical coordination number Z ₀ ~ 6.5–8.0 and by the slope of the cumulative ice-particle radial distribution function (RDF) C ~ 40–60. These micro-structural parameters determine the critical relative density at the snow-to-firn transition ρ ₀ ~ 0.7–0.75. Traditionally, the boundary between the two densification stages is assumed, after Anderson and Benson (1963), at a considerably lower relative density of 0.6 corresponding to the specific bend observed in many ice-core density profiles. Modeling by Salamatin and others (2006, in press) has confirmed the earlier finding by Ebinuma and co-workers (Ebinuma and others, 1985; Ebinuma and Maeno, 1985, 1987) that this first sharp decrease in the densification rate manifests only the onset of an intermediate regime, in which particle rearrangement and plasticity work together. The dislocation creep takes over, and the firn stage begins at the higher critical relative densities.

Thus, the critical density ρ ₀ becomes one of the principal microstructural parameters which control the snow/firn densification in modeling approaches (Arnaud and others, 1998, 2000; Salamatin and others, 2006, in press). The initial (surface) snow build-up and the evolution of the snow/firn structure with depth depend on ice formation conditions (Alley, 1988). Ice-core data analysis performed by Salamatin and others (in press) shows that higher critical densities generally correspond to higher temperatures T and higher surface snow densities ρ _s, although without clear quantitative correlation. Similar observations were earlier reported by Benson (1962) and Arnaud (1997), but the definition of the critical density was different. It was suggested that meteorological conditions such as wind speed, surface temperature, temperature gradients and insolation (e.g. Craven and Allison, 1998; Lipenkov and others, 1998; Bender, 2002; Raynaud and others, 2007) and, possibly, precipitation processes can affect the properties of the near-surface snow and, thus, the densification of snow/firn strata. As summarized in Table 1, two types of snow microstructures (L and H groups of ice cores) can be roughly distinguished on the basis of model constraining (Salamatin and others, in press). These structures are characterized by different best-fit critical coordination numbers Z ₀ and RDF slopes C, resulting in mean critical densities ρ ₀ ≈ 0.709 and 0.745, respectively. It was shown that the L group exhibits distinctly lower densification rates (i.e., a ‘harder’ structure) in comparison with the H group.

Table 1. Snow/firn densification parameters

A new microstructural characteristic, the critical bonding factor ζ ₀, was introduced (Salamatin and others, 2006) to describe the fraction of grain surface occupied by excess neck volume created due to pressureless sintering (e.g. through water-vapor transport) outside the plastically formed contacts. The value of this parameter was estimated as ζ ₀ = 0.55±0.05 without any noticeable correlation to ice formation conditions.

The goal of the present paper is to further investigate the snow/firn densification model (Salamatin and others, 2006) on the basis of scale analysis and to derive explicit semi-empirical relations for the close-off depth and ice age in quasi-stationary climatic conditions at a given close-off relative density ρ _c following, generally, the linear dependence on temperature as determined by Martinerie and others (1992, 1994).

Scale Analysis of the General Model

For quasi-stationary ice-formation conditions, at fixed temperature T and ice accumulation rate b, physical snow/ firn densification models (Arnaud and others, 2000; Salamatin and others, 2006) predict a certain similarity between different profiles of the relative density ρ (normalized by the pure ice density ρ _i) vs depth h. The critical relative density ρ ₀ appears in the above-cited papers in the constitutive relations for the macroscopic snow/firn compression rate ω as the typical scale of ρ, being close to the mean value of the relative density over the surface layer above the close-off level h _c.

The vertical velocity of a reference snow/firn particle is b/ρ, and, by definition,

(1)

where in a general form (Arnaud and others, 2000; Salamatin and others, 2006)

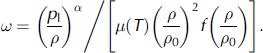
Here α is the creep index, μ is the Arrhenius-type temperature-dependent coefficient of non-linear viscosity in the ice-flow law, f is a function of ρ/ρ ₀, temperature, and microstructural parameters, and p _l is the load pressure calculated R as pl = gρi ^h ₀ ρ dh, where g is the gravity acceleration.

After substitution of the above expressions for ω and pl, in terms of scaled variables ρ̄ = ρ/ρ ₀ and h̄ = h/h _c, Equation (1) transforms to

(2)

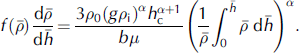
Integration with respect to h̄ from 0 to 1 and with respect to ρ̄ from ρ̄s = ρs/ρ0 (ρs is the relative density of surface snow) to ρ̄_c = ρ _c /ρ ₀ yields

(3)

where

Accordingly, if ρ ₀ represents the mean density of the snow/ firn layer above the close-off level then the ice age at pore closure t _c ≈ ρ ₀ h _c/b, and Equation (3) can be rewritten as

(4)

This defines the B_t factor and assumes that B_t ≈ B_h .

Based on the scale analysis, Equations (3) and (4) explicitly reveal the principal intrinsic links between the close-off characteristics (h _c, t _c), snow/firn rheological properties (α, μ) and climatic conditions (b, T). As a consequence, by definition, the shape factors of density–depth profiles B_t and B_h are expected to be constant or, at least, dependent only on structural characteristics (e.g. ρ ₀, ρ _c). Relations (3) and (4) were envisaged by Salamatin and others (in press). However, the coefficients B_t and B_h were introduced formally and estimated directly on the basis of ice-core data. They had different values for each of the two established L and H types of snow microstructures with noticeable (±5–10%) variations (see Table 1). In the following section, we use the snow/firn densification model to specify the B_t and B_h relationships.

Computational Experiments and Ice-Core Data

The physical snow/firn densification model (Salamatin and others, 2006) was constrained and validated on a representative set of ice-core density measurements at 22 sites in the Antarctic and Greenland ice sheets with wide ranges of present-day temperatures from –57.5 to –10^˚C and ice accumulation rates from 2.2 to 330 cm a^–1 (Salamatin and others, in press). The model parameters (i.e. the factor f (ρ̄) in Equation (2)) were tuned so as to fit the simulated density–depth curves to the experimental data. Here we describe a special series of computations performed with the recommended (mean) parameters from Table 1. We study the analytical expressions of the B factors in Equations (3) and (4) for different snow/firn structures, characterized by the critical densities v ₀, and possible variations of the close-off densities ρ _c.

Based on Martinerie and others (1992, 1994), a linear empirical correlation between the close-off relative density ρ _c and the firn temperature T (in K),

(5)

can be employed after Lipenkov and others (1999) to predict the close-off depth h _c and ice age t _c from the model and to

calculate the B_h and B_t values in Equations (3) and (4). Additionally, for each temperature, maximum deviations of ±0.01 from ρ _c given by Equation (5) are also tested.

In full agreement with the scale analysis, the calculations confirm that B_t and B_h do not directly depend on b or T and do not differ from each other by more than ±2% on average. Accordingly, the 22 best-fit ratios B_t /B_h inferred in Salamatin and others (in press) for Martinerie’s relation (5) are equal to 1 within the standard deviation of 1%.

The computational experiments at the creep exponent α = 3.5 reveal that a power approximation f ~ (ρ̄)² α ⁺¹ can be assumed. Hence, the integral of f (ρ̄) in B_h coefficient in Equation (3) is proportional to ( ρ _c /ρ ⁰ )^2α+2-( ρ _s /ρ ₀ )^2α+2, where the second term appears to be negligibly small. As a result, B_h does not depend on ρ _s and is found to be inversely proportional to ρ ₀ ². Finally, the proportionality between B_h and ρ _c ⁵ can be established directly from the simulations:

(6)

The analytical accuracy of this approximation is not worse than ±1% for B_t and ±3% for B_h . The best-fit estimates of the products B_hρ ₀ ²/ρ _c ⁵ and B_tρ ₀ ²/ρ _c ⁵ obtained in Salamatin and others (in press) are plotted against temperature T in Figure 1 by solid and open circles, respectively. The solid line in the figure corresponds to Equation (6) and practically coincides with the mean-square approximation (dashed line) of the observational data. The relative standard deviation does not exceed 2%. It is partly caused by local changes in snow/firn structures, i.e. in microstructural parameters Z ₀, C _, and largely by deviation of ζ ₀ from its mean recommended value 0.55 (see Table 1).

Fig. 1. The best-fit estimates of the products Bhρ ₀ ²/ρ _c ⁵ and Btρ ₀ ²/ρ _c ⁵ vs temperature T (solid and open circles) deduced by Salamatin and others (in press) from the 22 ice-core density profiles over the Antarctic and Greenland ice sheets at ρ _c given by Equation (5) as compared to Equation (6) (solid line) and the mean-square approximation (dashed line).

Thus, Equations (3), (4) and (6) consistently, within a few percent, predict the general close-off characteristics of the firn-to-bubbly-ice transition at given (present-day) climatic conditions b, T, provided that the critical density ρ ₀ and close-off density ρ _c of the snow/firn structure are known. The latter parameters, although rather stable, are primarily influenced by temperature and other meteorological conditions (Martinerie and others, 1992, 1994; Arnaud, 1997; Arnaud and others, 1998; Lipenkov and others, 1999; Raynaud and others, 2007; Salamatin and others, in press). ρ ₀ can be estimated on the basis of the data presented in Table 1, while ρ _c is conventionally determined by Equation (5).

Assuming that for a certain site under consideration the snow/firn structure development and the critical density do not change significantly with the climate, we can rewrite Equations (3–6) in terms of relative variations of the close-off characteristics for two different stationary conditions:

Here R _g = 8.314 J (molK)^–1 is the gas constant, and h ^* _c and t ^* _c are the close-off depth and ice age determined (measured) at the reference (present-day) ice accumulation rate b ^* and surface (firn) temperature T ^*. The apparent activation energy Q’_p ≈ 63.6 kJ mol^–1 is a modification of Q_p from Table 1 additionally corrected to take into account the dependence (Equation (5)) of ρ _c on temperature in Equation (6). This form of Equations (3) and (4) may be especially useful in paleo-reconstructions and sensitivity studies.

Density–Depth Profile

A simple analytical approximation of the density–depth profile for the snow/firn layer can be useful in applications. Based on ice-core measurements (Lipenkov and others, 1997) at Vostok station, Antarctica, an exponential presentation was proposed by Salamatin and others (1997) and confirmed by Ekaykin and others (2003). Subject to the condition that the critical relative density ρ ₀ equals the mean relative density of the snow/firn layer above the close-off level h _c, we can write this relationship as

(7)

where the densification factor γ is expressed via ρ _c and ρ ₀ by the following equation

(8)

which is a consequence of Equation (7) at h = h _c, where ρ = ρ _c. The parameter γ as a function of the righthand side of Equation (8) is plotted in Figure 2.

Fig. 2. The exponent factor γ as a function of the ratio (1 – ρ _c)/(1 – ρ ₀) on the righthand side of Equation (8).

To illustrate the applicability of Equations (7) and (8) in combination with Equations (3–6), two limiting cases of Antarctic ice cores from Vostok station (Lipenkov and others, 1997) and H72 site (Nishio and others, 2002) are considered as typical respective representatives of L and H groups. Present-day climatic conditions at these sites and close-off characteristics calculated from Equations (3–6) for the critical densities deduced in Salamatin and others (in press) are presented in Table 2. As expected, h _c and t _c do not differ by more than 2% from the corresponding best-fit estimates given in parentheses. However, the accuracy reduces to 3.5–5% if the mean critical densities for L and H structures from Table 1 are used in calculations. The relative density–depth profiles described by Equations (7) and (8) are compared with the observational data in Figure 3. These exponential curves predict the general course of the densification process quite well, but do not catch the initial depositional and/or diagenetic phase of the snow metamorphism (Alley, 1988) within a few (3–5) uppermost meters. In the case of the L group, under cold and low-wind conditions affected by insolation, a low-density firn microstructure is formed at decreased rates of the near-surface densification (see Fig. 3a). On the other side, the H group is characterized by the intense pressureless sintering in the near-surface snow layer, resulting in a high-density firn microstructure (see Fig. 3b).

Table 2. Climatic conditions and close-off characteristics at Vostok and H72 sites

Fig. 3. Comparison of the relative density–depth profiles predicted by Equations (7) and (8) at the Vostok (a) and H72 (b) sites with the observational data (Lipenkov and others, 1997; Nishio and others, 2002).

Conclusion

Simple relationships (3), (4) and (6) for the depth h _c and ice age t _c of the firn-pore closure are derived on the basis of the general snow/firn densification model (Salamatin and others, 2006). Together with Martinerie and others’ (1992, 1994) correlation (5) for the close-off relative density ρ _c, they allow an approximate, though fairly accurate (within a few percent), description of the densification process in quasi-stationary climatic conditions (b, T) with the firn structure specified by the critical relative density ρ ₀. The importance of this microstructural parameter was earlier emphasized by Arnaud and others (1998, 2000). As a first approximation, the mean ρ ₀ values for different L and H groups of site conditions (ice cores) can be taken from Table 1. The relative density–depth profiles are given by Equations (7) and (8), and the whole calculations can be easily performed with a standard spreadsheet. The results obtained can be especially useful in paleo-reconstructions and sensitivity studies.