Sensitivity of mountain glacier mass balance to changes in bare-ice albedo

Abstract

Albedo is an important parameter in the energy balance of bare-ice surfaces and modulates glacier melt rates. The prolongation of the ablation period enforces the albedo feedback and highlights the need for profound knowledge on impacts of bare-ice albedo on glacier mass balance. In this study, we assess the mass balance sensitivity of 12 Swiss glaciers with abundant long-term in-situ data on changes in bare-ice albedo. We use pixel-based bare-ice albedo derived from Landsat 8. A distributed mass-balance model is applied to the period 1997–2016 and experiments are performed to assess the impact of albedo changes on glacier mass balance. Our results indicate that glacier-wide mass-balance sensitivities to changes in bare-ice albedo correlate strongly with mean annual mass balances (r² = 0.81). Large alpine glaciers react more sensitively to bare-ice albedo changes due to their ablation areas being situated at lower elevations. We find average sensitivities of glacier-wide mass balance of −0.14 m w.e. a⁻¹ per 0.1 albedo decrease. Although this value is considerably smaller than sensitivity to air temperature change, we stress the importance of the enhanced albedo feedback that will be amplified due to atmospheric warming and a suspected darkening of glacier surface in the near future.

INTRODUCTION

Glaciers react to changing climatic conditions by losing or gaining mass. In recent years, global atmospheric warming enhanced glacier melts worldwide (Zemp and others, 2015). Rising air temperatures cause a prolongation of the melting season and, hence, a positive feedback on glacier volume loss. However, the strongest driver of mass balance on alpine glaciers is net shortwave radiation (e.g. Brock and others, 2000a; Klok and Oerlemans, 2004; Pellicciotti and others, 2008), mainly due to the fact that net longwave radiation is close to zero and the glacier surfaces are characterised by low albedo values in their ablation areas that are exposed over most of the summer season (Paul and others, 2008). This causes a strong, positive feedback that enhances surface melt significantly (Oerlemans and Hoogendoorn, 1989; Van de Wal and others, 1992; Paul and others, 2007) and shapes the spatial ablation pattern (Paul and others, 2005; Sugiyama and others, 2011; Naegeli and others, 2015).

In the past, several studies have investigated the mass-balance sensitivity on various climatic factors, i.e. changes in air temperature and precipitation (Oerlemans and others, 1998; Braithwaite and Zhang, 2000; Oerlemans and Reichert, 2000; Klok and Oerlemans, 2002; De Woul and Hock, 2005; Huss and Fischer, 2016). These studies reported mass-balance sensitivities to air temperature change of −0.2 to −2.0 m w.e. a⁻¹ C⁻¹ (on average ~ −0.7 m w.e. a⁻¹ C⁻¹) and sensitivities to precipitation change of +0.03 to +0.44 m w.e. a⁻¹ 10%⁻¹ (on average ~ +0.2 m w.e. a⁻¹ 10%⁻¹). Only few studies tackled the impact of changes in surface albedo in a similar way, but assessed different albedo parameterisation schemes and resultant mass-balance differences (e.g. Klok and Oerlemans, 2004; van Angelen and others, 2012) or linked albedo sensitivity to temperature changes. For example, Oerlemans and others (2009) stated that the observed bare-ice albedo decline of 0.17 between the years 2003 and 2006 on the tongue of Morteratschgletscher, Switzerland, is responsible for an additional cumulative melt volume of 3.5 m of ice, which resembles a temperature increase of +1.7 °C. Correspondingly, Machguth and others (2008) emphasised that uncertainty in albedo is one of the four most important factors influencing mass balance. Further, Klok and Oerlemans (2004) found that mass-balance sensitivity to temperature change is greatest in simulations in which bare-ice albedo is represented based on observations. With new satellite datasets, bare-ice albedo can accurately be derived in the spatial domain for a large sample of glaciers, thus facilitating a comprehensive impact analysis of ice albedo on glacier mass balance. Several studies have investigated the effect of impurities in snow and related impacts on albedo and melt rates (e.g. Doherty and others, 2010; Painter and others, 2012; Dumont and others, 2014; Gabbi and others, 2015), or have tested the performance of snow albedo parameterisations on calculated melt rates (e.g. Brock and others, 2000b; Klok and Oerlemans, 2004; Pellicciotti and others, 2005). In contrast, the effect of changing bare-ice albedo on glacier melt has been relatively poorly studied although its relevance is expected to increase in a warming climate. In this study, we aim at investigating the impact of knowledge on spatially distributed bare-ice albedo on glacier mass balance, separating it from the effect of potential changes in snow albedo.

Shortwave broadband albedo of bare-ice glacier areas is highly variable, both temporally (e.g. Oerlemans and Knap, 1998) and spatially (e.g. Naegeli and others, 2015). The presence of different materials on the ice surface, such as mineral dust, soot, debris or organic matter, strongly impacts on the local reflectivity characteristics and thus albedo (e.g. Chandler and others, 2014; Pope and Rees, 2014; Azzoni and others, 2016). Moreover, in different areas worldwide, a darkening of glacier surfaces, due to an increased abundance of allochthonous materials can be observed, as e.g. in Greenland (Dumont and others, 2014), the Himalaya (Takeuchi, 2001), the Swiss Alps (Oerlemans and others, 2009) or High-Mountain Asia (Wang and others, 2014). A direct feedback of increased climatic forcing on a lowering bare-ice albedo has not yet been proven but seems likely based on various lines of process linkages, such as more efficient accumulation of fine surface impurities, more (wind-)erodible sediments on slopes surrounding the glacier, the increased frequency of a liquid water film on the surface, and – possibly – better conditions for the reproduction of organic material on the ice surface (e.g. Hodson and others, 2007; Cook and others, 2012).

State-of-the-art mass-balance models are capable of calculating spatially distributed mass balance and are calibrated and validated with in situ point data (Hock, 1999; Klok and Oerlemans, 2002; Gabbi and others, 2014). However, most models use either constant values for the albedo of snow, ice and firn (e.g. Machguth and others, 2006) or parametrise the albedo of snow and ice based on empirical relationships (Arnold and others, 1996; Brock and others, 2000a; Gardner and Sharp, 2010). There are only few studies that used satellite-based spatially distributed broadband albedo as input for their mass-balance calculations. However, most of them are focusing on one or very few glacier(s) and/or 1 balance year only (Klok and Oerlemans, 2004; Paul and others, 2005; Machguth and others, 2008; Naegeli and others, 2015). Given the strong spatio-temporal variability of both bare-ice albedo and mass balance, an in-depth assessment of mass-balance sensitivity to albedo changes for different years and a larger sample of glacier is required to generalise the results.

Here, we use a large dataset of seasonal point mass-balance data obtained by the direct glaciological method for 12 Swiss glaciers in the western and southern European Alps to model their distributed annual mass balances over 20 years with pixel-based spatially distributed snap-shot bare-ice albedo. We examine the impact of locally explicit bare-ice albedo on modelled mass balances by comparing them to mass-balance values obtained using a constant albedo for clean glacier ice (α = 0.34) motivated by literature (e.g. Oerlemans and Knap, 1998; Cuffey and Paterson, 2010). We emphasise that, by purpose, we do not include spatially explicit snow albedo in our approach, allowing us to strictly focus on the impact of changing bare-ice albedo on mass balance. Moreover, we investigate these changes both in the temporal (20 years) and spatial dimensions (glacier-wide mass balance, elevation bands and balance gradients) to deepen our knowledge about the importance of the albedo parameter for mass-balance modelling. Furthermore, these investigations help to disentangle the mass-balance sensitivity on bare-ice albedo changes from changes in other climatic parameters (such as air temperature and precipitation) and enable us to highlight possibilities and challenges for modelling the future behaviour of glaciers in a warming climate.

STUDY SITES AND DATA

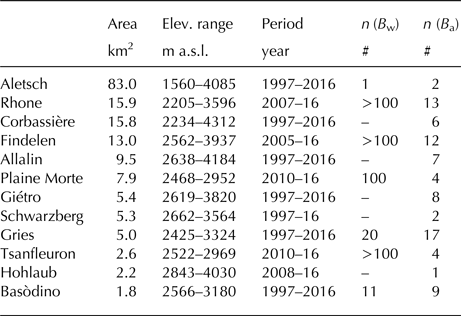
The study focuses on 12 alpine glaciers located in the western Swiss Alps (Fig. 1). Whereas Glacier de Tsanfleuron, Glacier de la Plaine Morte, Aletsch- and Rhonegletscher (west to east) are located in the northern Alpine ridge (cantons of Bern and Valais), Glacier de Corbassière, Glacier du Giétro, Findelen-, Schwarzberg-, Allalin-, Hohlaub-, Griesgletscher and Ghiacciaio del Basòdino (west to east) are situated in the southern Swiss Alps in the cantons Valais and Ticino. These greater areas differ considerably in their climatic characteristics. While the northern part of the study area shows high amounts of annual precipitation, and thus high accumulation and ablation rates (e.g. Tsanfleuron, Aletsch, Rhone), the southern part of the study area is characterised by the driest climatic conditions throughout the European Alps with low precipitation sums resulting in low accumulation rates (e.g. Findelen, Hohlaub). The long-term average equilibrium line altitude of the 12 glaciers therefore varies strongly from ~2900 m a.s.l. for Tsanfleuron to ~3400 m a.s.l. for Allalin (period 2010–16) (Glaciological Reports, 1999–2017). The glaciers range from ~2 km² (Basòdino) to ~80 km² (Aletsch) in area and cover an overall elevation range from ~1500 to 4300 m a.s.l. (Table 1). In general, the two last decades were characterised by mass loss and retreat of all 12 glaciers. For the period 2010–16, the average mass balance of all glaciers was −0.84 m w.e. a⁻¹, ranging from −1.35 m w.e. a⁻¹ for Tsanfleuron to −0.51 m w.e. a⁻¹ for Holaub.

Fig. 1. Study sites (lime dots) located in the western and southern Swiss Alps.

Table 1. Overview of the 12 study glaciers, their area, elevation range, the study period, the average number of winter mass-balance measurements n(B _w) per year and number of annual mass-balance measurements n(B _a) per year. Glaciers are ordered according to their surface area

Mass-balance data

For all glaciers, direct glaciological mass-balance measurements are obtained by various investigators (see Huss and others, 2015, for an overview). All 12 glaciers are part of the Swiss Glacier Monitoring Network (GLAMOS) and the mass-balance data are reported to the World Glacier Monitoring Service. Whereas the mass balance for seven glaciers is observed both in summer and winter, the remaining five glaciers are only monitored on an annual basis (Table 1). For some of the glaciers, such as Gries, Findelen and Rhone, an extensive monitoring programme with high numbers of winter snow probings, snow pits and summer ablation stakes exists. For others, such as Aletsch, only few point mass-balance measurements are available (Table 1). Monitoring on the individual glaciers was started between the 1920 and 2010 (Huss and others, 2015). For the present study, we consider a 20-year period (1997–2016). For five of the 12 glaciers, the study period is shorter (Table 1).

Satellite data

We examined eight end-of-summer (between mid-August to end of September) Landsat 8 scenes (path 195, row 28) between 2013 and 2016 for an optimal retrieval of bare-ice surface albedo. Based on cloud coverage and melt-out pattern the scene from 30 August 2015 was chosen to be most suitable for providing complete bare-ice albedo maps for all glaciers. At that date, the glaciers showed a maximum extent of the ablation area and no clouds obscured the glacier surfaces. The atmospherically corrected higher-level surface reflectance Landsat 8 data have a spatial resolution of 30 m and comprises seven spectral bands. Specific information about this data can be found in Vermote and others (2016).

Model input data

The mass-balance model (see the section ‘Methods’) requires meteorological input data at daily resolution. We used daily mean air temperature, total precipitation and average global solar radiation from different stations of the MeteoSwiss network. For each glacier, the closest and most representative station providing complete series for the individual variables was selected. Air temperature was extrapolated to the median glacier elevation using monthly lapse rates derived from surrounding stations.

For the entire study period, only one DEM was used per glacier. All DEMs have a spatial resolution of 25 m, mostly referring to the years 2007 or 2008, and are based on aerial photogrammetry (Bauder and others, 2007). We explicitly do not take into account changes in glacier extent and surface elevation during the study period in order to strictly investigate mass-balance changes triggered by shifts in bare-ice albedo only, but not by the dynamic response of the glacier. Thus, all results are reference-surface mass balances (cf. Cogley and others, 2011).

METHODS

Spatially distributed shortwave broadband albedo

For each glacier, a spatially distributed shortwave broadband albedo map was derived using the Landsat 8 scene. We applied the narrow-to-broadband conversion by Liang (2000) to obtain shortwave broadband albedo from the seven individual spectral bands. The formula was originally developed for Landsat TM/ETM data; however, we did not change the empirical weighting parameters specified in literature and solely assigned the corresponding band numbers of Landsat 8. Broadband albedo α is calculated as

(1) $$\eqalign{ \alpha = \; &0.356b_2 + 0.130b_4 + 0.373b_5 + 0.085b_6 \cr &+ 0.072b_7 - 0.0018,}$$

where b _n represents the spectral band number of Landsat 8. Naegeli and others (2017) highlighted the high accuracy of such albedo products and found a deviation of <0.001 in albedo on average compared with a more sophisticated albedo retrieval approach. Figure 2 shows the albedo distribution of three exemplary glaciers. Observed albedo in the ablation area of all glaciers is strongly variable in space, as the bare-ice surface of glaciers comprises a complex, heterogeneous mixture of different materials and structures. Typical albedo values in the ablation area are ~α = 0.2. This is substantially lower than recommended values for clean bare-ice albedo of α = 0.34 (e.g. Oerlemans and Knap, 1998; Cuffey and Paterson, 2010).

Fig. 2. Spatially distributed shortwave broadband albedo for Schwarzberg, Plaine Morte and Aletsch (see Fig. 1 for location). Note that the scale is enlarged for Aletsch.

Mass-balance model

To obtain spatially distributed mass balance from the point measurements performed on a seasonal to annual basis, a mass-balance model driven by daily temperature, precipitation and global radiation was applied (Huss and others, 2009, 2014). The relevant model components are summarised hereafter.

Snow accumulation C(x, y, t) for all grid cells (x, y) and all time steps (t) is calculated based on precipitation P occurring below a threshold air temperature of 1.5 °C (Hock, 1999). Accumulation distribution D(x, y) is inferred based on a spatial distribution pattern derived from winter snow measurements and topographic parameters (slope, curvature) to account for small-scale snow redistribution (Huss and others, 2009; Sold and others, 2016).

(2) $$C(x,y,t) = \; P(t)\; \times \; c_{{\rm prec}}\; \times \; D(x,y).$$

The factor c _prec allows adjusting precipitation sums measured at a weather station to the conditions on the glacier.

Snow and ice melt is calculated based on a simplified energy-balance formulation proposed by Oerlemans (2001), where the energy available for melt Q _M is defined as

(3) $$\eqalign{ Q_{\rm M}(x,y,t) = &(1 - \alpha (x,y,t))\; \times \; G(x,y,t) + k_0 \cr &+ k_1T(x,y,t).}$$

G is the global shortwave radiation in W m⁻², T the air temperature, and k ₀ and k ₁ represent parameters. This formulation approximates the longwave radiation balance and the turbulent heat exchange linearised around the melting point (Oerlemans, 2001; Machguth and others, 2006). We assume k ₀ = −55 W m⁻² to be constant for each glacier and fix it based on experience. Sensitivity tests showed that our results depend little on the choice of k ₀. The k ₁ is calibrated for each glacier and year, and has values of ~8–15 W m⁻² C⁻¹. Global radiation for all grid cells and days is calculated with

(4) $$G(x,y,t) = r(t)\; \times \; I_{{\rm pot}}(x,y,t)$$

with I _pot the potential clear-sky solar radiation computed on the basis of the DEM, and r(t) the daily ratio of observed to potential global radiation calculated from the weather station data. The local surface albedo α is taken to be constant for firn and bare-ice surfaces (α _firn = 0.53, α _ice = 0.34, most commonly applied literature values (e.g. Oerlemans and Knap, 1998; Cuffey and Paterson, 2010), or observed from satellite data, Fig. 2) and, for snow surfaces, is calculated based on the snow ageing function proposed by Oerlemans and Knap (1998). We adopt the parameters proposed in that study.

For each year and glacier, the model was individually calibrated based on all available seasonal/annual point mass-balance measurements. In a first step, observed precipitation was scaled by c _prec to match winter accumulation measurements (Eqn (2)). In a second step, the parameter k ₁ (Eqn (3)) was calibrated in an automated procedure to optimally match all observations of annual point mass balance (see Huss and others, 2015, for details). In this way, we constrained the model to agree with the seasonal measurements in each year ensuring a correct representation of the mass-balance components (accumulation, ablation). The parameters c _prec and k ₁ vary among all glaciers and years. Hence, they account for both the imperfection of the meteorological input as well as the mass-balance model to reproduce the glacier-specific observations. For glaciers with no winter accumulation data during the study period (Table 1), c _prec was assumed to be constant for every year and is estimated on the basis of alternative information, such as accumulation measurements on the respective glaciers before 1997 (Allalin, Schwarzberg, Hohlaub) or relevant literature (Giétro, Corbassière, Huss and others, 2015).

Model setup

To analyse the effect of spatially explicit bare-ice albedo, we developed the following model setup: In a first model run, the spatially distributed observed snap-shot bare-ice albedo derived from Landsat 8 was implemented and applied whenever a grid cell became snow-free (Fig. 3a). The date of snow depletion is directly provided by the model as a result of cumulative snow precipitation and melt over the season. Henceforth, this model run is termed R _α-vari. The parameters c _prec and k ₁ (Eqns (2) and (3)) for accumulation and melt, respectively, were calibrated for each year and glacier using the seasonal in situ point measurements. For the second model run, hereafter termed R _α-const, a constant bare-ice albedo based on e.g. Oerlemans and Knap (1998) or Cuffey and Paterson (2010) for snow-free grid cells was assumed (Fig. 3b). The parameters c _prec and k ₁ were taken from R _α-vari. In both model runs, the albedo of snow is represented in an identical fashion by using a snow ageing function (Oerlemans and Knap, 1998) and its effect on the mass balance will not be evaluated in the present study. R _α-vari can be considered as a reference run making use of optimal knowledge about bare-ice albedo for the determination of the model parameters and, hence, the computation of glacier-wide mass balance. Differences between R _α-vari and R _α-const solely stem from differences of observed and literature-based spatially-constant bare-ice albedo. Mass-balance changes between R _α-vari and R _α-const are indicative for the sensitivity of glacier mass balance to a change in albedo that might occur in response to atmospheric warming and the darkening of ice surfaces.

Fig. 3. Conceptual illustration of albedo input data and the model setup: (a) variable bare-ice albedo derived from Landsat 8, (b) constant albedo values for ice and firn, and (c) the setup of the two model runs.

RESULTS

For all 12 glaciers distributed annual mass balance was computed using the above methodology for the time interval 1997–2016 (or for the period with mass-balance observations, Table 1). For model run R _α-vari observed bare-ice albedo was used, whereas for model run R _α-const constant ice albedo was employed (Fig. 3). Differences in glacier-wide annual mass balance B _α-diff refer to these two runs (B _α-vari − B _α-const). We define mass-balance sensitivity to albedo change as the change in glacier-wide or local mass balance per 0.1 albedo decrease. When presenting average time series for all study sites, the early years (1997 to ~2007) consist of a smaller sample size than the years at the end of the study period (~2007–16, cf. Table 1).

Impact on glacier-wide mass balance

The time series of differences in glacier-wide mass balance between R _α-vari and R _α-const averaged over the 12 glaciers is highly variable and exhibits no temporal trend over the last two decades (Fig. 4a). However, mass-balance differences between the model runs R _α-vari and R _α-const are strongly correlated with the glacier-wide annual mass balance fluctuations over the study period (r ² = 0.89, n = 20, Fig. 4b). Hence, very negative balance years (1998, 2003, 2011, 2015) also show larger balance differences due to the positive feedback of the low bare-ice albedo in the ablation areas on melt rates. Moreover, the spread of the differences within the entire sample is greater, the more melt occurred in an individual year with standard deviations (std dev.) between 0.06 m w.e. a⁻¹ (2016) and 0.16 m w.e. a⁻¹ (2015). On average over the 20 years, the difference in annual glacier-wide mass balance between model runs assuming observed or constant bare-ice albedo is −0.20 m w.e. a⁻¹, with a minimum of −0.09 m w.e. a⁻¹ for Allalin and a maximum of −0.33 m w.e. a⁻¹ for Plaine Morte (cf. Table 2).

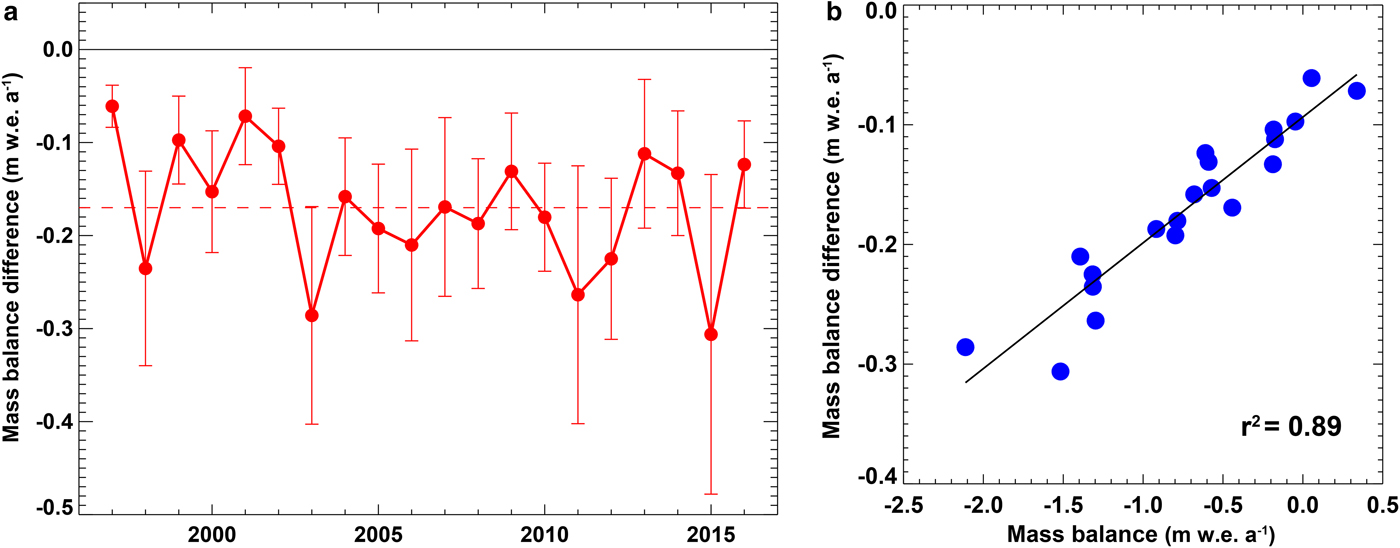
Fig. 4. (a) Times series of the difference in annual glacier-wide mass balance between B _α-vari and B _α-const averaged over all 12 glaciers. The error bars show ±1 std dev. of all glaciers. (b) Correlation between average mass-balance difference (B _α-diff = B _α-vari − B _α-const) and glacier-wide mass balances (n = 20).

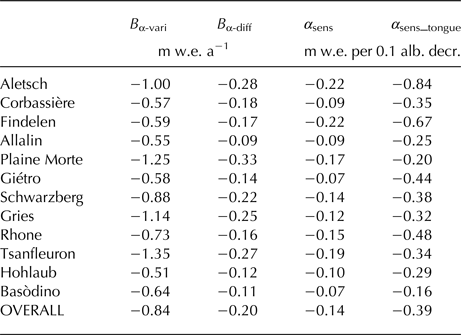
Table 2. Compilation of results for all study sites. Glacier-wide mean annual mass balance using the observed bare-ice albedo (B _α-vari) and the averaged mass-balance difference (B _α-diff = B _α-vari − B _α-const) are given as means over the observation period (Table 1). The mean sensitivity of glacier-wide mass balance to albedo change (α _sens), as well as the sensitivity for the lowermost 10% of the glacier's elevation range (α _{sens_tongue}) is stated. Average results (OVERALL) refer to the period 2010–16 that is covered by all glaciers.

Lower bare-ice albedo strongly influences the cumulative mass balance of individual glaciers (Fig. 5). Literature-based constant bare-ice albedo leads to smaller long-term mass loss (R _α-const) as model runs with observed bare-ice albedo values, typically being 0.1–0.2 lower in the ablation area of glaciers (R _α-vari).

Fig. 5. Cumulative mass balance obtained from different model runs for Gries.

The sensitivity of a glacier to a given change in bare-ice albedo is a measure of the expected glacier response to climate change if bare-ice albedo changes with atmospheric warming as was hypothesised by several recent papers (Oerlemans and others, 2009; Box and others, 2012; Dumont and others, 2012). Figure 6a demonstrates that small glaciers exhibit lower mass-balance sensitivities to albedo change than large glaciers. Time series for arbitrarily selected glaciers, however, show strong interannual fluctuations. Mass-balance sensitivity to albedo change significantly correlates with annual mass balance (r ² = 0.81, n = 20, Fig. 6b). The increasing sensitivity with glacier size is explained by different factors. Aletsch, with its glacier terminus at ~1600 m a.s.l., has large parts of its ablation area at low elevations, compared with Gries and Basòdino whose termini are located at ~2500 m a.s.l. The albedo feedback is active over a considerable portion of the year for large glaciers, thus impacting more strongly on glacier-wide mass balance in comparison with small glaciers where snow depletion on the glacier tongue may start only in August in some years. While the glacier-wide mass-balance sensitivity to albedo change is strongly influenced by glacier size and the glacier's mass balance (Fig. 6), the local mass-balance sensitivity at the glacier tongue mainly depends on the elevation range and local climatic characteristics. For example, Aletsch shows the largest mass-balance sensitivity for its terminus area (−0.84 m w.e. a⁻¹ per 0.1 albedo decrease (α _{sens_tongue}, Table 2) due to its very low elevation. Also, the mass-balance sensitivity for the terminus area of Findelen is high (−0.67 m w.e. a⁻¹ per 0.1 albedo decrease) although the glacier tongue is located 1000 m above that of Aletsch. This is attributed to generally low precipitation rates at Findelen and, hence, a rather long exposure of the bare-ice area. In contrast, Basòdino, whose ablation area is located at a similar elevation as that of Findelen (Table 1), shows considerably weaker mass-balance sensitivities to albedo change, both in the glacier-wide average (−0.07 m w.e. a⁻¹ per 0.1 albedo decrease) and for the terminus (−0.16 m w.e. a⁻¹ per 0.1 albedo decrease), which is likely related to the relatively high amounts of precipitation received by this glacier and comparably short exposure of the bare-ice area.

Fig. 6. (a) Time series of glacier-wide mass-balance sensitivity to albedo change for three selected glaciers with different characteristics (Basòdino, Gries and Aletsch), and (b) correlation between the average glacier-wide mass-balance sensitivity to albedo change and mean annual mass balance (n = 20).

Impact on spatial mass-balance distribution

The impact of using observed spatially distributed bare-ice albedo on mass-balance patterns is clearly visible if the results of the model runs R _α-vari and R _α-const are compared (Fig. 7). Mass-balance differences are strongest at the glacier terminus, whereas differences become smaller when approaching the equilibrium line. No differences are found for the accumulation area, which is snow-covered year-round, thus showing no sensitivity to changes in bare-ice albedo.

Fig. 7. Mass-balance difference map for the year 2015 (B _α-vari − B _α-const) for four selected neighbouring glaciers.

The Landsat 8 derived albedo maps result in a more heterogeneous ablation pattern than if a constant bare-ice albedo value is used. Hence, the local variations in mass-balance differences on the tongue of e.g. Allalin or Schwarzberg are in accordance with the spatial variability of shortwave broadband albedo (Fig. 2). For example, regions with higher local albedo on the central tongue area of Allalin, exhibit lower mass-balance differences between R _α-vari and R _α-const. Satellite-derived average broadband albedo for the areas below the median glacier elevation are between 0.08 (Findelen) and 0.22 (Gries) below literature-based bare-ice albedo (α = 0.34).

The increasing impact of bare-ice albedo on mass balance in the ablation area is highlighted if mass-balance differences are averaged in elevation bands (Fig. 8). Besides stronger mass-balance differences, their spread within the individual bands is significantly enhanced at lower elevations. These observations are both attributed to the prolonged exposure of bare-ice areas and the variability in observed bare-ice albedo in the ablation area.

Fig. 8. Mass-balance differences (B _α-vari − B _α-const) for Aletsch aggregated in 200 m elevation bands and 20 years. Solid red lines mark the median, the boxes refer to the 25–75% quantiles and the bars to the 5–95% quantiles of all values.

To further investigate the impact of observed bare-ice albedo on mass-balance distribution, we analyse the change in the vertical gradient of mass balance as an indicator for the glacier response time. Large gradients (strong changes in mass balance with elevation) indicate greater mass turn over and thus a more sensitive response to changes in climatic conditions (Oerlemans, 2001). Figure 9 illustrates the enhanced balance gradients in the ablation area, as already shown by Oerlemans and Hoogendoorn (1989) and Paul and others (2008), if lower albedo values are used in the modelling. In general, our mass-balance gradients correspond well with literature values (see e.g. Oerlemans, 2001).

Fig. 9. Mass-balance gradients with observed (red) and constant (blue) bare-ice albedo for two selected glaciers. The observed bare-ice albedo is given as mean ± 1 std dev.

DISCUSSION

The pixel-based spatially distributed snap-shot bare-ice albedo obtained from Landsat 8 (Fig. 2) used for the modelling is subject to some uncertainties. It is important to note that this study does not investigate changes in ice and/or firn albedo over time but relies on a snap-shot broadband albedo for ice in the modelling setup. A detailed discussion of the performance of the narrow-to-broadband formula (Eqn (1)) or the validation is beyond the scope of this paper, but we refer the reader to Naegeli and others (2017). We consider the Landsat 8 derived bare-ice albedo from the scene acquired on 30 August 2015 as representative for the entire study period. To investigate this assumption, we compared calculated bare-ice albedo for all eight evaluated Landsat 8 scenes (acquired in 2013–16) and found highly similar albedo patterns, particularly in the lowermost part of the ablation area (±1 std dev. of ~0.048 in pixel-based albedo). The individual albedo maps only varied significantly regarding the snowline positions, i.e. the fraction of the glacier providing information about bare-ice albedo. Uncertainties stemming from local factors influencing the retrieved bare-ice albedo such as cryoconite, organic matter or water present on the surface are not investigated here, although they are of great importance (Naegeli and others, 2015; Azzoni and others, 2016; Cook and others, 2016; Pope and others, 2016). Furthermore, the Landsat 8 scene for 30 August 2015 was finally selected as the largest part of the glacier was free of winter snow due to strong melting during the year, thus maximizing the observability of ice albedo.

Uncertainties in the mass-balance model, regarding the representation of snow accumulation, snow albedo and the calculation of snow and ice melt might importantly influence the results. Especially, the simplified nature of the approach to calculate the energy available for melt (Eqn (3)) has the potential to cause uncertainties. For a two-decadal period and a large set of glaciers, however, the input data for driving a more physically-based energy-balance model is not available at the spatial scale. Performing a complete uncertainty analysis of all modelling components is not possible within the present study. However, we note that our strategy to closely constrain the model with measured seasonal mass balances will strongly reduce the impacts of model input assumptions.

We observed elevation-dependent mass-balance differences (Fig. 8) that are qualitatively linked with the overall albedo pattern present on a glacier and are strongly influenced by the exposure time of bare ice during the ablation period. The lowermost bare-ice areas that exhibit the lowest shortwave broadband albedo values (Fig. 2), are affected by the albedo feedback for the longest time interval over a year, thus reacting the most sensitively to the prescribed bare-ice albedo changes (see α _sens__tongue in Table 2). Earlier studies reported an elevation-dependent mass-balance sensitivity to a 0.1 albedo decrease of −2.0 to −0.5 m w.e. a⁻¹ for entire mountain glaciers in Austria and Canada considering both snow and ice albedo changes (Oerlemans and Hoogendoorn, 1989; Munro, 1991). Also accounting for changes in snow albedo explains the two to three times larger sensitivities in comparison with our study, as lower snow albedo induces an earlier melt-out and thus another feedback on ice melt besides the direct effect of lower bare-ice albedo. Changes in snow albedo are, however, driven by different processes and are not the focus of this paper.

Our definition of mass-balance sensitivity to bare-ice albedo changes enabled us to analyse the glacier's sensitivity independently from changes in air temperature or precipitation. Compared with published mass-balance sensitivities to air temperature and precipitation change, the sensitivity to bare-ice albedo is intermediate. We found an average sensitivity of glacier-wide mass balance of −0.14 m w.e. a⁻¹ per 0.1 albedo decrease. This is about five times less than the sensitivity to a 1° air temperature change and about in the same order as a 10% precipitation change (Oerlemans and others, 1998; Braithwaite and Zhang, 2000; Oerlemans and Reichert, 2000; Klok and Oerlemans, 2002; De Woul and Hock, 2005; Huss and Fischer, 2016). However, a direct comparison of these values is questionable as these parameters (air temperature, precipitation and albedo) strongly modulate and interact with each other (see e.g. Klok and Oerlemans, 2004). With global warming, a prolongation of the ablation season and a shift in the snowline is expected. Bare-ice areas are thus increasingly exposed and albedo feedbacks are enhanced. In addition, the accumulation of mineral dust and organic matter in the ablation area of glaciers is hypothesised to lead to a darkening of the ice surface, further impacting on the mass losses of glacier tongues within the next years (e.g. Cook and others, 2016; Tedesco and others, 2016). Whether and to what degree a warming climate with a possible darkening of the glacier surface impacts on the mass-balance sensitivities evaluated here for present-day climate conditions is still unclear and hardly predictable. We therefore suggest to gain better process understanding regarding the causes that alter glacier surface albedo (e.g. the presence of water on bare-ice surface and its diurnal cycle, the abundance of cryoconite and other factors) and to establish a quantitative overview of the darkening phenomenon of alpine glaciers in a spatially distributed manner to be able to consider these feedback mechanisms in, e.g., modelled future runoff from alpine catchments. To tackle the need of better representing the full albedo feedback in mass-balance models, further attempts should be made to encompass and derive shortwave broadband albedo of glacier surfaces from satellite data. An operational data product suitable for mountainous areas, e.g. based on Landsat 8 and/or Sentinel-2 satellite data (Naegeli and others, 2017), would be highly beneficial and could facilitate the spatial and temporal representation of albedo variations in mass-balance models.

CONCLUSIONS

Based on spatially distributed snap-short bare-ice albedo derived from Landsat 8 and a wealth of point mass-balance data from 12 Swiss glaciers, we assessed the mass-balance sensitivity to changes in bare-ice albedo over a time interval of two decades. Our methodology and the setup of the model runs allowed us to investigate glacier-wide mass-balance differences between runs with observed bare-ice albedo in comparison with literature-based constant albedo on an annual basis, as cumulative time series, as well as spatially distributed and aggregated in elevation bands.

Differences in glacier-wide mass balance for the 12 glaciers between 1997 and 2016 show strong interannual variability, the variance being explained by 89% by annual mass balances. The mass-balance sensitivity to bare-ice albedo changes is stronger for larger glaciers as their low-elevation areas are affected by the albedo feedback for a longer time period. However, local climatic conditions, in particular the amount and timing of snow fall events, strongly impacts on the sensitivity of an individual glacier, independent of its size and elevation range.

We found an average mass-balance sensitivity of the investigated glaciers of −0.14 m w.e. a⁻¹ per 0.1 albedo decrease. This is considerably less than mass-balance sensitivity to air temperature change and in the same order as precipitation change reported in literature. However, with a warming climate, the ablation period in the Alps is prolonged and snow lines are rising, whereas at the same time different processes might lead to a further darkening of bare-ice surfaces. This results in an enhanced albedo feedback and amplifies the sensitivity of mountain glaciers to surface albedo, which has to be taken into account for modelling future glacier behaviour.