Seismic evidence of mechanically weak sediments underlying Russell Glacier, West Greenland

Abstract

Amplitude-versus-angle (AVA) analysis of a seismic reflection line, imaged 13 km from Russell Glacier terminus, near the western margin of the Greenland ice sheet (GrIS), suggests the presence of sediment at the bed. The analysis was complicated by the lack of identifiable multiples in the data due to a highly irregular and crevassed ice surface, rendering deeper seismic returns noisy. A modified technique for AVA processing of glacial seismic data using forward modelling with primary reflection amplitudes and simulated multiple amplitudes is presented here. Our analysis demonstrates that AVA analysis can be applied to areas with noisy seismic returns and indicates that sediment underlies the seismic study site. Our data are inconsistent with the common assumption that the GrIS is underlain only by hard bedrock, but consistent with the presence of subglacial sediment with porosity between 30% and 40%. As analysis and modelling of ice-sheet dynamics requires a sound knowledge of the underlying basal materials, subglacial sediment should be taken into account when considering ice dynamics in this region of the GrIS.

Introduction

Basal boundary conditions provide a first-order control on the stability of an ice mass. Specifically, the physical character and rheology of the ice/bed interface are pertinent for understanding and predicting subglacial hydrological evolution and how it influences the dynamic response of an ice sheet. The morphology of the subglacial environment has been used as a direct attribute of basal boundary conditions in ice-flow models (e.g. Payne, 1999; Pattyn and others, 2005). Furthermore, the dynamic impact of subglacial hydrological systems is argued to be substantially different for sediment-based systems (e.g. Darcian flow drainage (Clarke, 1987) and sediment canals (Walder and Fowler, 1994; Ng, 2000)) in contrast to hard-bed drainage systems (e.g. linked cavities (Iken and Bindschadler, 1986) and channels (Röthlisberger, 1972)). Seismic reflection studies have been used to assess subglacial material characteristics (e.g. Blankenship and others, 1986; Smith, 1997), and amplitude vs angle (AVA) techniques have been applied to determine subglacial sediment properties such as till porosity and acoustic impedance (e.g. Peters and others, 2007, 2008; Booth and others, 2012). Here we present a modified AVA technique that involves forward modelling using primary amplitudes, due to a lack of identifiable multiples in the data. We apply the technique to a seismic reflection experiment located 13 km from the margin of the Greenland ice sheet (GrIS), where the ice is ∼640m thick. Our inferences suggest the presence of sediment at this ice/bed interface.

Field Site

The field site, SHR, is located on land-terminating Russell Glacier in the ablation zone of the GrIS (67806’ N, 49°55’W; Fig. 1) at an average surface elevation of 710 ma.s.l. SHR is of particular interest for examining the links between ice dynamics and basal properties as it was the site of both the highest observed mean annual velocity (138ma^–1) and the largest summertime acceleration (300%) along this flowline (known as the K-transect), during the period 1990-2007 (Van de Wal and others, 2008). This region also experiences diurnal uplift and horizontal acceleration directly coupled to surface melt volumes (Shepherd and others, 2009). In summer 2010, two boreholes were drilled to the bed at depths of 610 and 632 m, and instrumented with an array of pressure sensors and thermistor strings (Smeets and others, 2012).

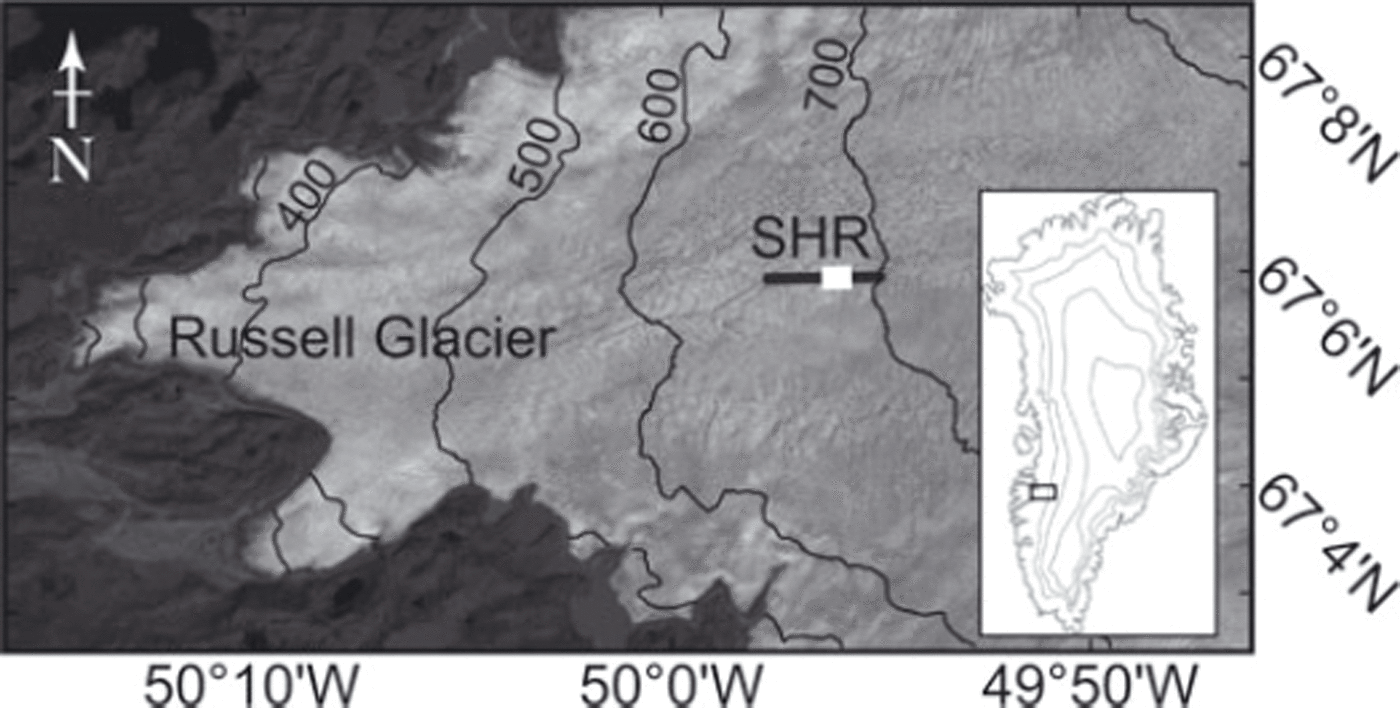
Fig. 1. Landsat image of Russell Glacier acquired on 18 August 2010 (at a resolution of 30 m) with the inset indicating the location in Greenland. Surface elevation contours are marked by the black curves at 100 m intervals. The location of the seismic reflection line is indicated by the black line; the thick white line indicates the area of the bed sampled by the seismic profile.

Data Acquisition

A seismic AVA experiment was carried out at SHR in late July 2010. The seismic line was oriented parallel to bulk ice flow (approximately northeast-southwest). Data were recorded using a Geometrics GEODE system, with 24 vertical-component 100 Hz geophones installed at 10m intervals in a fixed array configuration. To increase coupling with the ice surface, geophones were mounted on 7 cm thick, 10 kg concrete slabs that were allowed to freeze in overnight. A total of 33 shots were installed at 3 m depth with a horizontal separation of 60 m, covering 1920 m on the surface; with a lack of firn in late July, deeper shot holes were not deemed necessary. Each hole was loaded with a combined 250g Pentalite and 400g dynamite charge, attached to electrical detonators with a 25 ms delay. The west side of the seismic line comprised 19 shots, with a maximum surface offset of 1140 m from the first geophone. The east side of the seismic line was made up of 13 shots with a maximum surface offset of 780 m from the first geophone (Fig. 2a). Approximately 1100m of the ice/bed interface was illuminated along the profile with a threefold coverage. The maximum offset-to-depth ratio was 2.2, with a continuous nominal angular coverage of 0–35°. Elevations of the geophones and shot locations were surveyed using a Leica SR520 GPS receiver, differentially corrected against a bedrock-mounted reference station, to 10cm precision. Unlike flat, snow-covered terrain where reflection seismic acquisition more typically takes place (e.g. Anandakrishnan, 2003; Smith, 2007; Peters and others, 2008), the surface topography at SHR undulates substantially, with ice ridges rising to several meters (see Fig. 2a). In the vicinity of the seismic line, crevasses, moulins and surface streams were observed.

Fig. 2. (a) Ice surface elevation at SHR. Note the vertical exaggeration and scale on the elevation axis. (b) Seismic profile of the field site indicated in Figure 1. The depth is based on a seismic velocity of 3800 m s–¹ and is relative to the surface elevation in (a). (c) Interpretation of the main features in the seismic profile. AVA analysis is applied to the area shown by the black double arrow.

Seismic Stacked Section

The seismic stacked section was processed using ReflexW (Sandmeier Software; Table 1), assuming a seismic compressional (P-)wave velocity of 3800 m s^–1. Due to the irregular surface topography, the signal-to-noise ratio of the seismic returns was degraded by near-surface defocusing (see Fig. 3a for a representative shot gather). Crevasses and moulins were a potential source of additional diffractions within the data. As a result, the seismic returns are noisy in comparison with data collected from further inland on the GrIS (Booth and others, 2012) or the Antarctic (e.g. Smith, 2007; Peters and others, 2008). Notwithstanding, the ice/bed interface is distinct across most of the stacked section (Fig. 2b and c). Up-glacier, in the eastern part of the seismic section, the bed appears to be flat, with relatively minor undulations on the vertical scale of ∼10m. Ice thickness across the section is ∼640 m. A weaker cross-cutting event appears in the stacked section, likely due to an out-of-plane reflection, but will not impact our results as we concentrate analysis only on the non-contaminated areas of the flat reflection. A second weak reflection underlies the ice/bed interface, which is not a ghost reflection due to the shallow depth of the shot holes, but may be a reflection from an underlying horizon (Fig. 2b and c).

Table 1. Processing procedures for the seismic stacked section shown in Figure 2

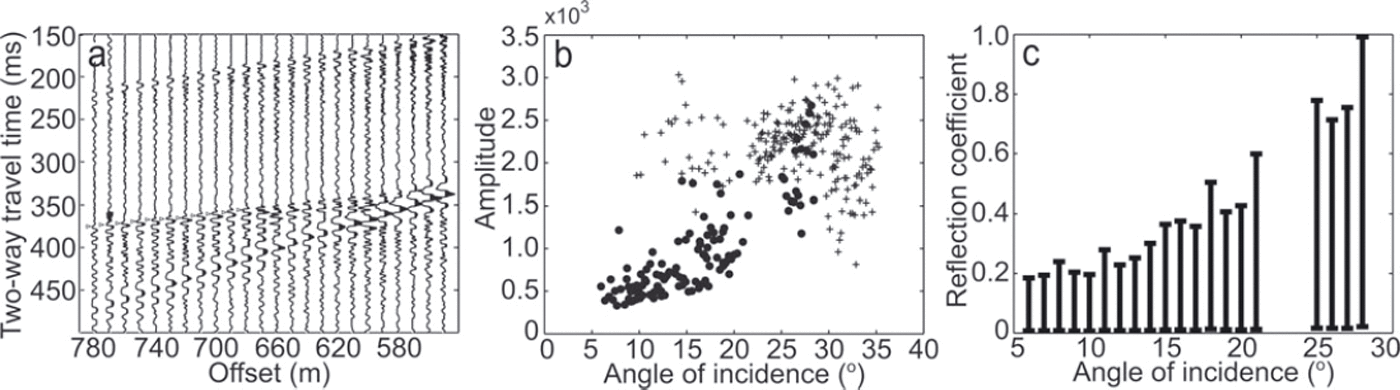
Fig. 3. (a) Shot gather from SHR where it can be seen the basal reflection shows no polarity reversal. AVA picks are shown by the triangles. Note that data affected by the ground roll are not picked. (b) Example of primary reflection amplitudes corrected for geometrical spreading and an illustrative attenuation of 0.4 km^T1. Amplitudes are divided into east data (dots) and west data (crosses; see Fig. 2). (c) A graph showing the range of simulated AVA outputs for SHR using a range of multiple and attenuation values, binned into angles of 1 °.

Amplitude-Versus-Angle (AVA) Analysis

In AVA analyses, the change in the seismic reflectivity of the ice/bed interface is calculated with respect to changing angle of incidence, producing an AVA response curve. The ‘reflection coefficient’ is a function of the properties of the two interface materials, including their density and P- and shear (S-)wave velocities (Aki and Richards, 1980). As it is possible to estimate these characteristics for the overlying ice, the observed AVA response curve can be diagnostic of the nature of the substrate. We thus aim to apply this analysis to the seismic reflection data from SHR in order to determine the basal material characteristics at this site. Following Peters and others (2008), the reflection coefficient, as a function of incidence angle, R(θ), can be calculated with

(1)

where A_p is the amplitude of the primary arrival, d_p is the total travel distance of the primary arrival, a is the attenuation coefficient for ice and A₀ is the source amplitude at normal incidence. Geometrical spreading is compensated for within Eqn (1) through d_p and a. While we are able to measure the primary reflection amplitudes A_p and calculate the travel distance of the associated ray paths d _p, we do not have direct knowledge of the source amplitude A ₀ in Eqn (1). Fortunately an estimate of A ₀ can ordinarily be obtained from the ratio of the squared primary amplitudes of the ice/bed reflection to their corresponding first multiple (A _m) at normal incidence using:

(2)

Assuming that Eqn (1) can then be applied, a forward modelling approach is subsequently used to match the observed AVA response curve, with the best-fit AVA curve modelled using the Knott-Zoeppritz (K-Z) equations (CREWES source code). AVA curves are modelled by varying the P- and S-wave velocities and the bulk densities of the overlying ice and its substrate (Aki and Richards, 1980), where any combination of these three parameters uniquely identifies the substrate as, for example, hard bedrock, water, dilatant sediment or non-deforming sediment.

Unfortunately in the present case, the seismic data acquired at SHR are sufficiently noisy that multiple amplitudes cannot be reliably measured, so that application of Eqn (2), and subsequently of Eqn (1), is not feasible since A _m is unknown. To circumvent this problem we propose a new approach that exploits the fact that A_m can only vary within a narrow range for any given reflection event in order to still be physically plausible, as explained in detail below. The new approach consists of four main steps:

1. 1. Using a fixed, known, value of A_p and a narrow, physically plausible, range of A_m we use Eqn (2) to calculate an associated range of source amplitudes (A₀) for any particular reflection event.

2. 2. We subsequently insert known A_p, known d_p, a range of plausible a values, and the inferred range of A0 into Eqn (1), yielding a series of ‘simulated AVA curves’ for any such event.

3. 3. We then generate a cumulative plot of all simulated AVA response curves for all ice/substrate reflection events covered by our seismic survey at SHR (Fig. 3c).

4. 4. Finally we adapt the forward modelling approach, comparing the cumulative simulated AVA curves with a range of AVA curves modelled using the K-Z equations that are dependent on ice and substrate seismic velocities and densities; our approach is demonstrated schematically in Figure 4.

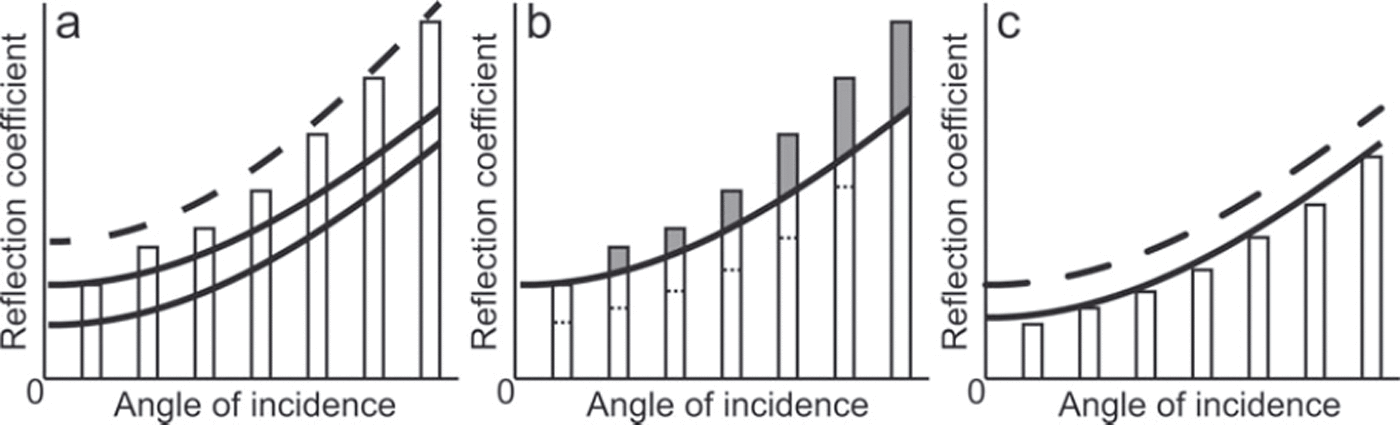
Fig. 4. Schematic of the procedure for comparing the simulated AVA range and the Knott-Zoeppritz (K-Z) AVA curves. (a) The dashed K-Z AVA curve R(0) lies above the simulated AVA R(0) and is therefore rejected. The solid K-Z AVA curves lie below the simulated AVA R(0) and are therefore retained. (b) The grey areas of the simulated AVA range bars are rejected as they lie above the R(0) range of the K-Z model. The dashed lines indicate where the simulated AVA range lies once all curves with any R(0) above the K-Z curve are rejected. (c) The solid K-Z AVA curve and the simulated AVA range are all within the same range, and the K-Z curve can then provide limits on the basal material properties at our site.

As we will demonstrate, visual matching of physically plausible simulated and modelled AVA curves is able to constrain the nature of the substrate at SHR, despite the uncertainty inherent to our new approach (see Fig. 5).

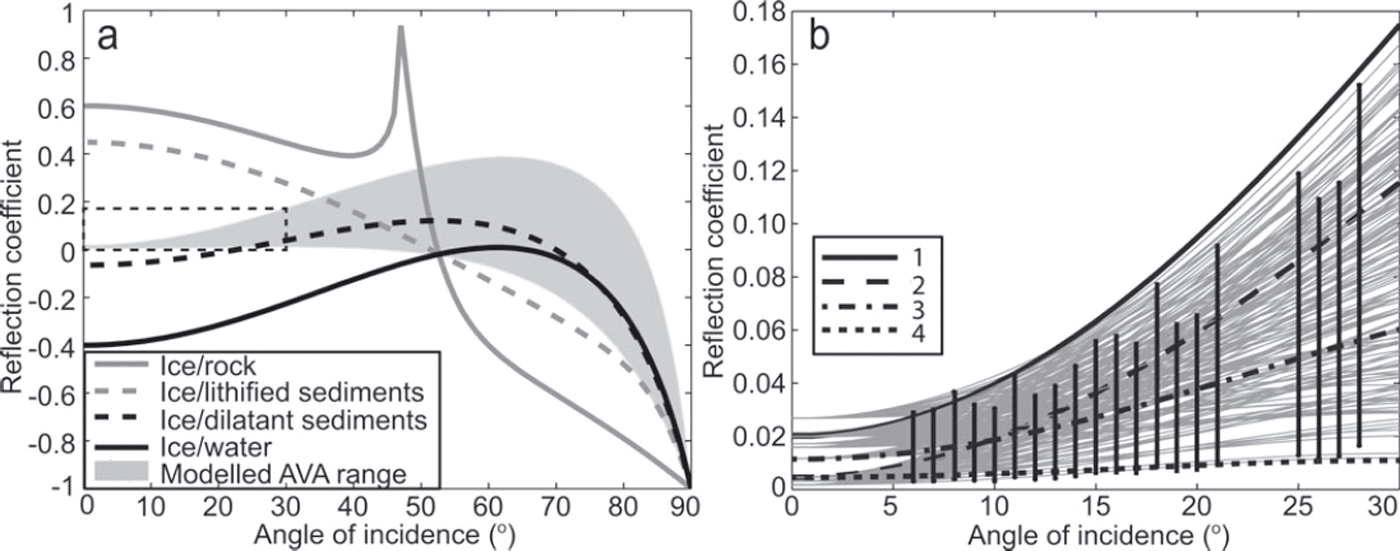
Fig. 5. (a) The range of K-Z models that correspond with our simulated AVA range at SHR (grey shaded zone) along with examples of reflection coefficient outputs for typical ice/interface boundaries using the K-Z equations. Here AVA curves for ice with bedrock, sediment and water interfaces are plotted using material properties as stated by Peters and others (2008). The dashed box indicates the area highlighted in (b). (b) A close-up of our simulated AVA range (black bars) that correspond to K-Z models (grey curves) within the simulated AVA R(0) range. Properties of selected curves, labelled 1–4, are shown in Table 2.

For the SHR dataset, measured seismic amplitudes were balanced to correct for variations in geophone coupling and shot power by normalizing each trace by the root-mean-square direct-wave amplitude (Booth and others, 2012). Primary reflection amplitudes were then picked at the peak of the first half-cycle from shot gathers, separated by the west (crosses) and the east (dots) gathers (divided by the location of the first geophone; an example of the primary reflection amplitudes corrected for geometrical spreading using an illustrative attenuation value of 0.4 km^r-1 is shown in Figure 3b, although our final analysis uses a range of attenuation values). A representative shot gather, with AVA picks indicated by triangles, is shown in Figure 3a. The reflection amplitudes from the east side of the seismic line exhibit a positive near-linear relationship with respect to increasing angles of incidence whereas, likely due to the cross-cutting event, reflection amplitudes from the west side of the seismic survey lack a clear relationship with angle of incidence. As a result, we concentrate our analysis on the east side of the line. In the eastern gathers, data quality between angles of 0–68 and 22–248 was sufficiently poor due to noise and ground-roll that they are not analysed.

We establish our plausible range of A _m values to apply to Eqn (2) by first examining the absolute value of the maximum primary reflection amplitude within the range 6–108, which is 595; no data are available between 0 and 68. We therefore test multiple amplitudes (A _m) within the range 0–600, but impose several constraints based on our AVA observations:

1. 1. No polarity reversal is observed, either with respect to the direct wave or across the offset range of the dataset (Fig. 3a). This suggests that the minimum reflection coefficient at the base of the ice is 0, therefore multiple amplitudes that deliver normal-incidence R(0) < 0 are rejected.

2. 2. A bedrock substrate has a normal-incidence reflectivity R(0) = 0:6 (Peters and others, 2008). As subglacial materials will not have a higher normal-incidence reflectivity than bedrock, any multiple amplitude that delivers R(0) > 0:6 is rejected.

3. 3. The seismic wavelet cannot have a higher amplitude than that which was initially radiated (i.e. A _p(θ)d _p(θ)e^{a d p9(Φ)} > A0), hence any multiple amplitude that delivers R(0) > 1, at any incidence angle, is rejected.

For each A _m test value, the attenuation coefficient (a) is varied between 0.2 and 0.6 km^{- 1}. The lower bound of 0.2 km^{- 1} , calculated by Bentley (1971) for cold Antarctic ice, represents a lower-end estimate of attenuation at the SHR site, where the ice is polythermal. The upper bound of 0.6 km^{- 1} was derived by Kohnen (1969) for the GrIS. Because ice temperature data are not available at SHR, we use this wide attenuation range, which is then reflected in the uncertainty of the final property estimation. The accepted range of simulated AVA observations, binned into angles of 1°, is shown in Figure 3c, and suggests that the normal-incidence reflectivity, R(0), at SHR lies within the range 0.00-0.19.

We now compare our simulated AVA range with known properties from K-Z AVA curves. Figure 5a shows typical outputs from K-Z models with the upper layer defined as ice (P-wave velocity 3800 ms^-1; S-wave velocity 1900 ms^{- 1} ; density 920 kgm^{- 3} ). Characteristics of the substrate are taken from Peters and others (2008). The ice/rock curve in Figure 5a has a strongly positive intercept at normal incidence, a shallow gradient and a critical refraction at an incidence angle of ∼47°. An ice/water boundary, on the other hand, is dominated by a negative reflection coefficient for all measurable angles of incidence because the acoustic impedance of water is substantially lower than that of ice, which results in a phase reversal of seismic reflections when imaging subglacial water bodies (Peters and others, 2008). Between ice/water and ice/rock AVA responses, all plausible scenarios are governed by sediment characteristics.

For SHR we calculate K-Z curves for an upper ice layer and a lower layer with P-waves ranging between 1600 and 5200 ms^-1, S-waves between >0 and 2800 ms^-1 and densities between 1000 and 2700 kgm^{- 3} , at intervals of 100 that allow for the possibility of sediment or rock at the interface. We constrain the K-Z models that are comparable to our simulated AVA range by imposing the following criteria that are schematically illustrated in Figure 4:

1. 1. The K-Z R(0) value must lie within the R(0) range output for the simulated AVA values with a tolerance of ±0.005, reflecting the maximum interquartile variability in any simulated AVA bin (see Fig. 4a).

2. 2. The binned AVA values must lie within the K-Z curve R(0) range with a tolerance of ±0.005 (see Fig. 4b).

3. 3. The SHR ray-path- and attenuation-corrected primary amplitudes (Fig. 3b) increase with angle of incidence and we therefore reject any K-Z R(0) curve that decreases between 0 and 30°.

4. 4. K-Z models with S-wave velocities of 0 ms^-1 and densities lower than 1000 kgm^{- 3} are rejected, as both imply the presence of free water, which is not consistent with the lack of polarity reversal in the primary amplitudes.

Figure 4c illustrates the conditions under which a K-Z curve would be accepted in our analysis. Comparison of the range of K-Z models that correspond to the simulated AVA range (Fig. 5) yields the following characteristics for the substrate at SHR: an acoustic impedance between 3.50 and 3.68 x 10⁶ kg m ^{- 2} s^{- 1} and a Poisson’s ratio (related to the level of saturation in a material) between 0.36 and 0.49, with the latter calculated using

(3)

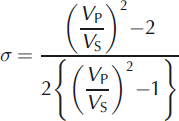
where VP is the P-wave velocity and V _S is the S-wave velocity (ms^{- 1} ). Illustrative examples of reflection curve properties from our simulated AVA range are given in Table 2, in relation to curves 1–4 highlighted in Figure 5b, to demonstrate the change in curve shape with variation in P-wave and S-wave velocities and density. In general, steeper gradients are associated with a lower S-wave velocity. The illustrative curves are deemed plausible by our analysis although curves 1 and 4 are close to the limit of the acceptable range of AVA outputs. As such, the velocity and density values for the curves illustrate the uncertainty estimates within our approach. An acoustic impedance and Poisson’s ratio value is calculated for each individual curve in Figure 5b. The final ranges of acoustic impedance of 3.50-3.68 x 10⁶ kg m ^{- 2} s^{- 1} and Poisson’s ratio of 0.36-0.49 are therefore determined from the entire acceptable range of AVA curves and thus incorporate the uncertainty from the approach.

Table 2. Reflectivity curve properties for illustrative curves highlighted in Figure 5b

Discussion and Conclusions

The SHR field site proved challenging for seismic analysis due to the highly variable surface topography and the presence of crevasses creating substantial noise within the dataset. We present a modified technique for AVA analysis using forward modelling with primary amplitude inputs that allows appraisal of the substrate from a seismic record with poorly defined or indistinguishable multiple reflections. Some properties of the basal material can be initially assessed from the primary reflection amplitude and the range of reflection coefficients. For instance, the absence of a polarity reversal throughout the dataset is inconsistent with the presence of a resolvable water body or dilatant till at the ice/bed interface. However, the positive gradient (as visible for the black dot data points in Fig. 3b) implies a high Poisson’s ratio that suggests the presence of water within a sediment matrix (Anandakrishnan, 2003). The limit of seismic resolution means that only layers thicker than approximately one-quarter of the seismic wavelength can be distinguished. Sediment layers of <1-2m thickness would not appear as individual layers at SHR, but could interfere with the seismic wavelets reflecting from underlying layers (Booth and others, 2012). Even considering these potential thin-layer effects at SHR, the primary amplitude polarity and gradient with respect to angle indicates that sediment is present at the ice/bed interface.

If the primary reflection amplitude is assumed to be unaffected by thin-layer effects, our range of acoustic impedance and Poisson’s ratio for SHR can be interpreted. Atre and Bentley (1993) suggest that lodged till has an acoustic impedance of 3.69-3.9 x 10⁶ kg m ^{- 2} s^–1 and a corresponding porosity of <0.3. In contrast, saturated and possibly deforming sediment is argued to have an acoustic impedance of 3.00-3.4 x 10⁶kgm^{r 2}s^–1 (Atre and Bentley, 1993) and a porosity of 0.4 (Smith, 1997). Hence, the acoustic impedance range of 3.50-3.68 x 10⁶ kg m ^{- 2} s^-1 at SHR suggests that, at the time of the seismic experiment, the till was not stiff enough to be lodged but had a high porosity between 30% and 40%. As the shear strength of sediment reduces exponentially with increasing porosity (Tulaczyk and others, 2000), the till was likely weak, although not dilated. The SHR Poisson’s ratio between 0.36 and 0.49 indicates water was present in the sediment (Gercek, 2007), as do water pressures near overburden recorded in the SHR boreholes at the time of the seismic survey (Smeets and others, 2012). The dashed box in Figure 5a, which indicates our simulated AVA range, clearly shows that the subglacial material at SHR is sediment.

The presence of subglacial sediment within 13 km of the glacier terminus suggests that the assumption of subglacial drainage over a hard bed in this region (e.g. Bartholomew and others, 2010; Schoof, 2010; Sundal and others, 2011) is incorrect. Given that SHR experiences significant seasonal and diurnal horizontal and vertical acceleration that is coincident with surface meltwater production and delivery (Van de Wal and others, 2008), it is likely that sediments play a critical role in the ice-sheet dynamics in this region. Sediment layers have also been identified under Jakobshavn Isbræ, West Greenland (Clarke and Echelmeyer, 1996; Block and Bell, 2011), although the extent and physical character of the sediment is debated. Further research is necessary to determine the role of sediment at the base of the GrIS for ice dynamics and sediment deformation/basal lubrication. The current study is confined to a ∼500 m section of the central flowline of Russell Glacier, and it is likely that sediment layers are variable in extent and thickness. Nevertheless, the existence of a layer of basal sediment at SHR indicates that studies which attempt to combine subglacial hydrology and ice dynamics in this region should account for the presence of till and its rheological characteristics.

Analysis of a seismic reflection line, 13 km from Russell Glacier terminus, West Greenland, demonstrates the presence of weak sediment at the bed with porosity between 30% and 40%. A seismic stacked section illuminating 1100 m of the bed reveals a largely smooth ice/bed interface at ∼640 m depth. AVA analysis is complicated by the lack of multiples in the data due to highly undulating surface topography. Our technique for AVA processing using forward modelling with primary reflection amplitudes and simulated multiple amplitudes indicates that, even considering the effect of possible thin layers, sediment underlies the study site and should be considered in analyses of ice dynamics in this region.