Reconstruction of snow/firn thermal diffusivities from observed temperature variation: application to iceberg C16, Ross Sea, Antarctica, 2004–07

Abstract.

Two inverse methods are proposed as a means of estimating the thermal diffusivity of snow and firn from continuous measurements of their temperature. The first method is applicable to shallow depths where temperature experiences diurnal variations, and is based on the fact that phase and amplitude of these diurnal variations are functions of the thermal diffusivity. The second method is applicable to the deeper part of the firn layer, and is based on a simple least-squares estimation technique. The methods applied here differ from various methods used for borehole paleothermometry in that observations are continuous in time and performance constraints on model/data misfit can be applied over a finite temporal period. Both methods are tested on temperature records from thermistor strings operating in the upper 2.5 m of firn on iceberg C16 (Ross Sea, Antarctica) from 2004 to 2007. Results of the analysis show promise in identifying melting events and the movement and refreezing of meltwater within the snow/firn layer.

Introduction

Snow and firn evolution are extremely important in numerous problems such as ice-sheet mass-balance evaluation (Zwally and others, 2005), ice-core dating and the determination of the age difference between ice and enclosed gas (Schwander and others, 1997; Blunier and others, 2004). The energy and mass balances of snow and firn determine the coupling between the overlying atmosphere and the underlying ice mass. To adequately assess these balances in predictive models of ice-sheet behavior, the thermal properties (e.g. heat capacity and heat conductivity) of snow and firn must be known in a detailed and quantitative manner.

Thermal properties of snow and firn strongly depend on numerous factors (temperature, density, grain structure, etc.) and therefore vary with both position and time within the snow/firn layer. The problem of determining snow/firn thermal properties and especially their relation to other snow/firn parameters is of long-standing interest, and has been addressed using various approaches involving field observations, laboratory experiments and theoretical studies (Devaux, 1933; Yen, 1962; Mellor, 1977; Fukusako, 1990). The most widespread result from previous studies is the parameterization of heat capacity and thermal conductivity as functions of snow/firn density and temperature (e.g. Albert and McGilvary, 1992; Paterson, 1994; Schwander and others, 1997).

The many technical difficulties encountered in snow/firn study have limited direct in situ observation of snow/firn heat capacity, conductivity and diffusivity over continuous and extended time periods. In situ measurements can, for example, be obtained from snow pits excavated in the surface of ice sheets and glaciers. This observation process is good for establishing the instantaneous initial conditions of the snow/firn at the time of excavation. Long-term study of the site (e.g. involving instruments deployed in the pit and left behind to record subsequent changes) may also be useful, especially as the snow and firn structure of the back-filled pit evolves over long periods towards its original undisturbed state. We nevertheless acknowledge that this long-term observation process is itself imperfect, as the presence of the instruments themselves and the physical disconformity of snow used to back-fill the excavated pit will hamper analysis. In the present study we develop the methodology and examine the suitability (including problems associated with deployment) of determining thermal diffusivity in snow/firn from continuously monitored temperature probes inserted into the snow/firn layer.

Here we develop two methods to reconstruct the thermal diffusivity from temperature. The first method is applicable to shallow snow/firn layers where temperature experiences diurnal (or other ambient short-term) variation. This technique is based on the fact that amplitude and phase of the temperature variations at different depths are functions of the snow/firn thermal diffusivity. The second method is developed for deep snow/firn layers, with no restrictions on the timescale of temperature variations. This second technique is similar to a control method developed by MacAyeal and others (1991) for examination of temperature profiles in deep boreholes. The purpose of both methods is to find the distribution of the thermal diffusivity in space and time that best allows a solution of the heat diffusion problem to match observed temperatures.

Both methods were applied to snow/firn temperatures measured on an iceberg (C16) originating from the Ross Ice Shelf, Antarctica. This iceberg is currently adrift in the Southern Ocean off East Antarctica (66 ^◦ 52 ^′ S, 151.52 ^◦ 31 ^′ W, as of 30 April 2007). However, over much of the study period, it was located in the extreme southwest corner of the Ross Sea (77 ^◦ 6 ^′ S, 167 ^◦ 53 ^′ W), where it spent 5 years aground on a seabed shoal just north of Ross Island. Twice during this period (once in November 2004 and once in November 2005), thermistor strings were installed in the upper 2.5 m of the snow/firn near an automatic weather station (AWS) site located near the center of the approximately 15 km by 30 km iceberg. The first thermistor string operated from 1 November 2004 to 28 October 2005, at which point it was damaged during an effort to maintain the AWS station. The original string was replaced by the second thermistor string in November 2005, and this string continues to operate to the present time (March 2008).

Both strings have 12 thermistor probes and were installed in firn pits 2.5m deep. Thermistors were Campbell Scientific model 107 temperature sensors with accuracy ±0.01 ^◦ C. Temperature readings were made using Campbell Scientific data logger and multiplexer, models CR10X and AM16/32A, respectively. Spacing of the thermistor probes was variable, gradually increasing from 7 cm at the top to 50 cm at the bottom of the snow pits. The frequency of temperature measurement was 20 min.

To exclude changes in spacing between thermistors caused by firn compaction, thermistors were mounted on a wooden pole in a manner that placed them directly into the snow-pit wall. The pole itself was suspended from the AWS tower to prevent its vertical movement relative to the firn which supports the tower (the tower base was anchored to a 1 m by 1 m plywood plate and was buried 3 m below the firn surface). Both pits were refilled by snow originally excavated from the pits, which had been milled to constant grain size and packed to constant density. To account for stratigraphic and temperature disturbances resulting from the snow-pit backfill, initial data were discarded (approximately 10 days). As previously mentioned, both thermistor strings were installed in the immediate vicinity (less than 5 m) of an AWS that collects meteorological data (air temperature at two levels, pressure, wind speed, relative humidity, incident solar flux and net snow accumulation) and global positional system (GPS) position (latitude and longitude). All data are transmitted from the iceberg through the Argos satellite system.

Two shallow (4.5m) firn cores were extracted at the same time as the thermistor strings were installed, to obtain snow/ firn density and to identify ice layers resulting from refreezing of downward-percolating meltwater. The firn core extracted in 2005 had higher density and more ice layers than the core from 2004, indicating that during the austral summer of 2004 the iceberg was considerably warmer than in previous summers.

Inversion Method 1: Diurnal Variation

Two methods have been developed for analyzing the thermistor string data. The first is valid for shallow snow/firn depths and exploits diurnal variations in surface temperature which penetrate these depths. A reason to focus on daily variation is that longer (e.g. annual) periods exceed the timescales over which snow and firn evolve physically (i.e. densify; Anderson, 1976), and this can lead to estimates of the thermal parameters which are too coarse.

Analysis of the temperature data clearly shows the presence of diurnal variations during the austral-summer daylight when solar heating of the surface would vary over 24 hour periods. These diurnal variations were not observed during the austral-winter polar night season. Figure 1b shows the 6 day temperature record of the two upper thermistors located 7 and 15 cm below the surface. This temperature behavior resembles propagation of the temperature oscillations in the semi-infinite domain with periodic boundary conditions often studied in textbook examples. The analytical expression that describes this temperature oscillation (Tikhonov and Samarsky, 1999, p. 256) is:

Fig. 1. (a) Snow/firn temperature ( ^◦ C) observed at 7 cm depth. (b) Diurnal temperature variations at 7 and 15 cm depth. The phase of diurnal variation in the 15 cm temperature record (green) is shifted by ∼3 hours relative to the 7 cm record (blue). (c) A spectrogram depicting signal at 7 cm depth; the color bar shows the 10log of the power spectrum as a function of period and time. Warm color (deeper red) indicates that the signal varies strongly at the associated period range through the given time period. Periods of strong diurnal variation in the 7 cm temperature record are indicated by ellipses.

(1)

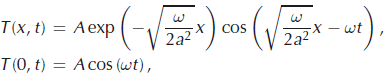
where T (x,t) is the deviation of temperature from a time-average mean expressed as a function of depth x and time t , A is the amplitude of the deviation from the mean temperature at the surface x = 0, ω is the frequency of temperature oscillations and a ² is the thermal diffusivity of a medium defined by

(2)

where k is the thermal conductivity, C _p is the heat capacity and ρ is the density. (Thermal diffusivity is written as the square of a variable a to indicate that it is a positive quantity.)

As can be appreciated from the exponential term in the above expressions, the amplitude of temperature oscillation decreases with depth. The times when the oscillation reaches its maximum and minimum at a given depth are shifted relative to the surface forcing. This phase shift is expressed by

(3)

As can be seen from Equations (1) and (3), thermal diffusivity a ² defines both the decay of amplitude and the phase shift.

Heat exchange between the atmosphere and the underlying snow/firn layer is a complicated process that includes many components (absorption of solar radiation, air ventilation through pore space, sublimation, etc.). Variation of the amplitude with depth is therefore determined by all processes, not only heat diffusion, making calculation of the thermal diffusivity from the amplitude less reliable.

In contrast, variation of the phase shift with depth is fairly constant during the period when strong diurnal variations in surface temperature are observed. The phase shift variability could be induced if other thermodynamic processes (e.g. absorption of solar radiation or vapor circulation) had strong periodicity other than 24 hours. As spectral analysis shows, during the austral summer the 24 hour period is dominant (it has 95% of the power spectrum). Determination of the thermal diffusivity from the phase shift (Equation (3)) is therefore more robust than from the temperature amplitude decay. We note, however, that this method cannot be used for media experiencing phase transitions: melting or refreezing in the case of snow and firn.

Our procedure for retrieving the heat diffusivity from the phase shift of temperature oscillations involves spectral analysis of temperature records at various depths. We represent the results of spectral analysis using spectrograms (Fig. 1c), which are widely used in seismology for understanding seismic signals. A spectrogram shows the distribution of the power spectrum in frequency (period) as a function of time. Spectrograms created using 20min snow/firn temperature time series (using a 7 day window) confirm the dominant diurnal periodicity of the upper snow/firn layers, validating the applicability of our method.

Having identified the depths where diurnal periods dominate, we then calculate the phase at each depth and determine the thermal diffusivity of the snow/firn layers in question using Equation (3). To perform this calculation, we estimate the phase shift between two neighboring thermistors and, using the expression

where Δφ is the estimated phase shift and Δx is the distance between two thermistors, determine bulk heat diffusivity for the layer of snow/firn between the two thermistors.

An example of thermal diffusivity reconstruction at 7–15 cm and 70–85 cm depths is shown in Figure 2. During the period when diurnal variations were dominant in the upper firn layer, snowfall was rarely detected by the AWS. We therefore neglected the effect of changing surface geometry in our analysis. As mentioned above, the proposed method cannot be applied in circumstances of melting/refreezing. Therefore, variations of several orders of magnitude during a period when melting temperatures are recorded in the firn cannot be considered valid. (For simplicity, we refer to melting temperatures as ‘non-negative’; such temperatures were registered down to 35 cm depth on several occasions.) However, such large variations can be useful as indicators of melting/refreezing.

An observation of such behavior at depths where temperature is below freezing (Fig. 2b) would signify the downward movement of meltwater, thus providing information about the temporal and spatial extent of melting/refreezing. Magnitudes of the thermal diffusivity at times when melting and refreezing were absent tend to be lower than those calculated using the density-dependent thermal diffusivity parameterization described by Yen (1962) and Fujita and Ageta (2000) and applied to the observed densities at the AWS site.

Fig. 2. Reconstructed thermal diffusivity (m²s ^{− 1}) for firn layers in the (a) 7–15 cm and (b) 70–80 cm ranges. Vertical lines denote periods when non-negative (T ≥ 0 ^◦ C) temperature was recorded by the whole thermistor string. Horizontal lines denote the range of thermal diffusivities associated with the snow/firn density dependencies found by Yen (1962) and Fujita and Ageta (2000).

According to Yen (1962),

where ρ is in g cm ^{− 3}, and

where ρ ⁱ is ice density and C _i and C _a are heat capacities of ice and air, respectively. According to Fujita and Ageta (2000),

Analysis of the temperature data obtained from C16 using the above method yields the following results. First, snow/firn temperature and atmospheric temperature experience diurnal oscillation during the austral summers from mid-October until the end of March. Diurnal temperature oscillations in 2005/06, which registered no deeper than 0.7 m, were shallower compared to 2004/05 when diurnal temperature oscillations were registered at 1.1 m depth. Diurnal temperature variations were not registered during the 2006/07 austral summer, due to the fact that the iceberg drifted out of the Ross Sea to a location where it experienced strong precipitation.

The snow-depth measurements from the AWS suggest that the thermistor string was buried under ∼2–2.5m of new snow which extinguished diurnal temperature variations at the various thermistor levels below. The comparison of the thermal diffusivity fields for the 2004/05 and 2005/06 austral summers shows that the melt season in 2004/05 was at least 10 days longer and the thermal diffusivity was higher by a factor of 2–4 at corresponding depths. A possible explanation for this difference could be the occurrence of strong melting during the 2004/05 austral summer which resulted in increased firn density and reduced pore space in the firn structure.

The fact that iceberg C16 experienced surface melting during the 2004/05 and 2005/06 austral summers does not allow the presented method to be applied efficiently. It is likely that the method described here is more suitable for low-latitude, high-altitude glaciers and the deeper interior of Antarctica, where surface melting is rare.

Inversion Method 2: Using a Control Method

The second method presented here does not impose conditions on the temperature variations and is similar to a control method developed by MacAyeal and others (1991) (see also Wunsch, 1988) for reconstruction of past surface temperatures from borehole temperature profiles. The object is to determine the variation of thermal diffusivity through space and time which minimizes the least-squares performance constraint J, describing the misfit between calculated and observed temperature:

(4)

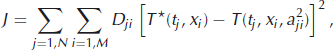
where T^* (tj,xi ) is the temperature measured by a thermistor located at depth x_i and time t_j , T(t_j ,x_i ,a ² _ji ) is temperature calculated as a function of thermal diffusivity a ² _ji using the heat diffusion model described below and D_ji is an element of a covariance matrix describing measurement uncertainties (http: //geosci.uchicago.edu/∼drm7/ research / InverseBook. pdf).

(5)

where ϵ is a matrix of temperature-dependent error measurements (ϵ_ji = 0.01 ^◦ C for T(t_j ,x_i ) > −35 ^◦ C and ϵij= 0.03 ^˚ C _ij for T (t_j , x_i ) < −35 ^˚ C) and \⟨·⟩ is the covariance operator. The forward heat diffusion model used in this study is

(6)

(7)

(8)

(9)

where x ₀ and x ₁ are the top and bottom boundaries of the domain, respectively, t ₀–t ₁ is the period over which the reconstruction is performed, T ₀ and T ₁ are observed temperature from the top and bottom thermistors of the studied domain and T _in is the vertically interpolated initial temperature derived from the measurements at t = t ₀.

The spatial domain is taken to be from x ₀ = 70 cm depth to x ₁ = 250 cm depth in order to reduce the effects of other processes influencing firn temperature (solar absorption, sublimation, wind ventilation, etc.) and minimize the effects of melting/refreezing.We assume that these additional complex processes influencing heat diffusion can be lumped together and treated with an effective heat diffusivity a ² _eff that is identified with a ² _ji in Equation (4). We finally assume that the error in observations used to specify initial and boundary conditions is too small to influence the calculated temperature field.

Following MacAyeal and others (1991), we use Lagrange multipliers and conjugate gradients to find the minimum of J with respect to a _eff . Minimizing the performance index with respect to a _eff rather than a ² _eff ensures that the effective heat diffusivity is a positive, physically meaningful quantity. The minimization procedure involves the following steps that are repeated iteratively until the minimum of J is found.

1. 1. Calculate the temperature distribution in the space–time domain ([x ₀,x ₁] × [t ₀,t ₁]) from Equations (6–9) using a finite-difference method from either the effective heat diffusivity from the previous iteration or an estimate of its initial distribution.

2. 2. Calculate J using Equation (4) (see below).

3. 3. Calculate the gradient of the performance index ∂J/∂(a _eff ) _ij .

4. 4. Update (a ² _eff ) _ij using a method to search for an improved value down the gradient of the performance index found in the previous step.

5. 5. Interpolate (a ² _eff ) _ij to the finite-difference grid (see below).

The expression for J given by Equation (4) is conditioned by the fact that temperature measurements from the thermistor string are available pointwise at specific depths, not continuously in space. We can therefore compare calculated and observed temperatures at these specific depths only. Updates of the gradient of the performance index and the thermal diffusivities are available only for these same specific depths. To obtain diffusivity values for depths other than those of the thermistor probe, we interpolate a ² _eff using the cubic spline method. This interpolation method was chosen to ensure the continuity of ∂a ² _eff /∂x required by Equation (6).

Results of the thermal diffusivity reconstruction using the above control method are shown in Figure 3b. The discrepancy between calculated temperature field with reconstructed thermal diffusivities and observed temperature does not exceed 0.2 ^˚ C, except at depths and times affected by refreezing and storms when the reconstructed firn diffusivity was several times that of ice. Overall, reconstructed firn diffusivities were less than the thermal diffusivity for solid, fully densified ice (1.225×10 ^{− 6} m²s ^{− 1}). There were periods (zones 1 and 2 in Fig. 3), however, when this presumed upper bound was exceeded. The most obvious reason for this excess is that processes other than heat diffusion dominated the energy balance at certain times and within certain depth ranges. For example, high values of the thermal diffusivities in zone 1 (Fig. 3b) are probably associated with refreezing of downward-percolating meltwater generated in the upper layer (Fig. 3a, zone 1).

Fig. 3. (a) Observed temperature ( ^˚ C) from 17 November 2004 until 30 April 2007. (b) Reconstructed thermal diffusivity (×10 ^{− 6} m² s ^{− 1}) for the 0.70–2.5m depth range. Black line on the color bar indicates ice value (1.225×10 ^{− 6} m² s ^{− 1}). Zones labeled 1 denote the influence of meltwater freezing. Zones labeled 2 indicate the influence of severe storms.

As mentioned previously, evidence that meltwater reached the depth of zone 1 was observed in snow-pit stratigraphy dug near the thermistor site in November 2005. Unexpectedly high values of the reconstructed diffusivity in zone 2 (Fig. 3a and b) are most likely associated with effects of a severe storm, where the wind speed recorded by the AWS exceeded 40 ms ^{− 1}.Wind speeds of this magnitudemay have caused an abrupt rise of the snow/firn temperature because of wind ventilation (Albert and McGilvary, 1992). The maximum misfit between modeled and observed thermistor temperature during the storm was 3 ^◦ C.

Conclusions

Two methods for reconstructing the thermal diffusivity of snow/firn from temperature measurements have been developed and applied to snow/firn temperature observations in the surface layer of iceberg C16.

The first method is applicable to shallow depths. The timing of large variations in thermal diffusivity (by several orders of magnitude) appears to be diagnostic of melting/refreezing events within the snow/firn layer. Therefore, this method could also be useful for determining the length of the melt season and estimating the minimum depth where melting/ refreezing occurs.

The second method is a least-squares method similar to those used in borehole temperature studies. This method is more general and can be improved with better knowledge of energy transfer processes in snow and firn. Improvements to the methodology described here should focus on the forward model used to calculate temperature (e.g. by including treatment of additional heat-transfer processes such as meltwater movement and ventilation) and on improving boundary conditions.