Plateau icefields as contributing areas to valley glaciers and the potential impact on reconstructed ELAs: a case study from the Lyngen Alps, North Norway

Abstract

Plateau icefields occur commonly in glacierized areas and not uncommonly in glaciated mountains. We report on a glacierized area of plateaux and valleys centred round the highest peak Jiehkkevárri (1833 m) in the maritime Lyngen Alps, North Norway. Some valley glaciers are fed by steep, narrow plateau glacier outlets and/or ice avalanching from the plateaux over precipitous cliffs. Plateaux must therefore be considered as “contributing areas”, if they supply ice to valley systems below. Equilibrium line altitudes (ELAs) are calculated for the valley glaciers during the Little Ice Age (LIA), accounting for both input and no input of ice from plateaux above. The results show that ELAs may be at significantly higher altitudes when plateau/x are contributing ice mass. The response of plateau glaciers to climate amelioration since the end of the LIA is somewhat different to that of valley glaciers, which appear to be retreating markedly. These findings have significant implications for the interpretation of moraine systems, glacier dynamics, the construction and reconstruction of present and former ELAs, and palaeoclimates in glacierized and glaciated mountain plateau areas.

Introduction

Contemporary glaciological investigations have an important role to play in understanding the dynamics of ice masses, in predicting the response of ice masses to future climate change (natural or anthropogenic), and for the accurate reconstruction and interpretation of former phases of glacierization. In many glacierized landscapes, plateau icefields act as accumulation sources for ice which feeds down through valley-head outlets or over precipitous icefalls into surrounding valleys, as in parts of North Norway (Gellatly and others, 1986; Gordon and others, 1987; Whalley and others, 1989, 1996). There has been only limited investigation of the dynamics of these ice bodies and their role in the mass balance of the valley glaciers (Gordon and others, 1987; Whalley and others, 1989, 1996; Rea and others, 1998). This paper investigates the glacierized area of plateaux and valleys centred around the highest peak, Jiehkkevárri (1833 m), in the south of the maritime Lyngen Alps, North Norway (Fig. 1) (all mountain and glacier names are taken from Series M711 Edition 4-Nor, 1:50 000 topographic maps). For comparison, equilibrium line altitudes (ELAs) are calculated for the glaciers during the Little Ice Age (LIA), accounting for both ice-mass input from plateaux and no ice-mass input from plateaux, i.e. assuming alpine-style glaciers. The results show that if an alpine, rather than contributing plateau and valley style of glaciation is identified, the reconstructed ELAs will be erroneous. The size of the plateau/x contributing to the valley glaciers and the altitudinal drop between the plateau/x and valleys affect the size of this error. Such errors will have consequent impact on climate interpretations.

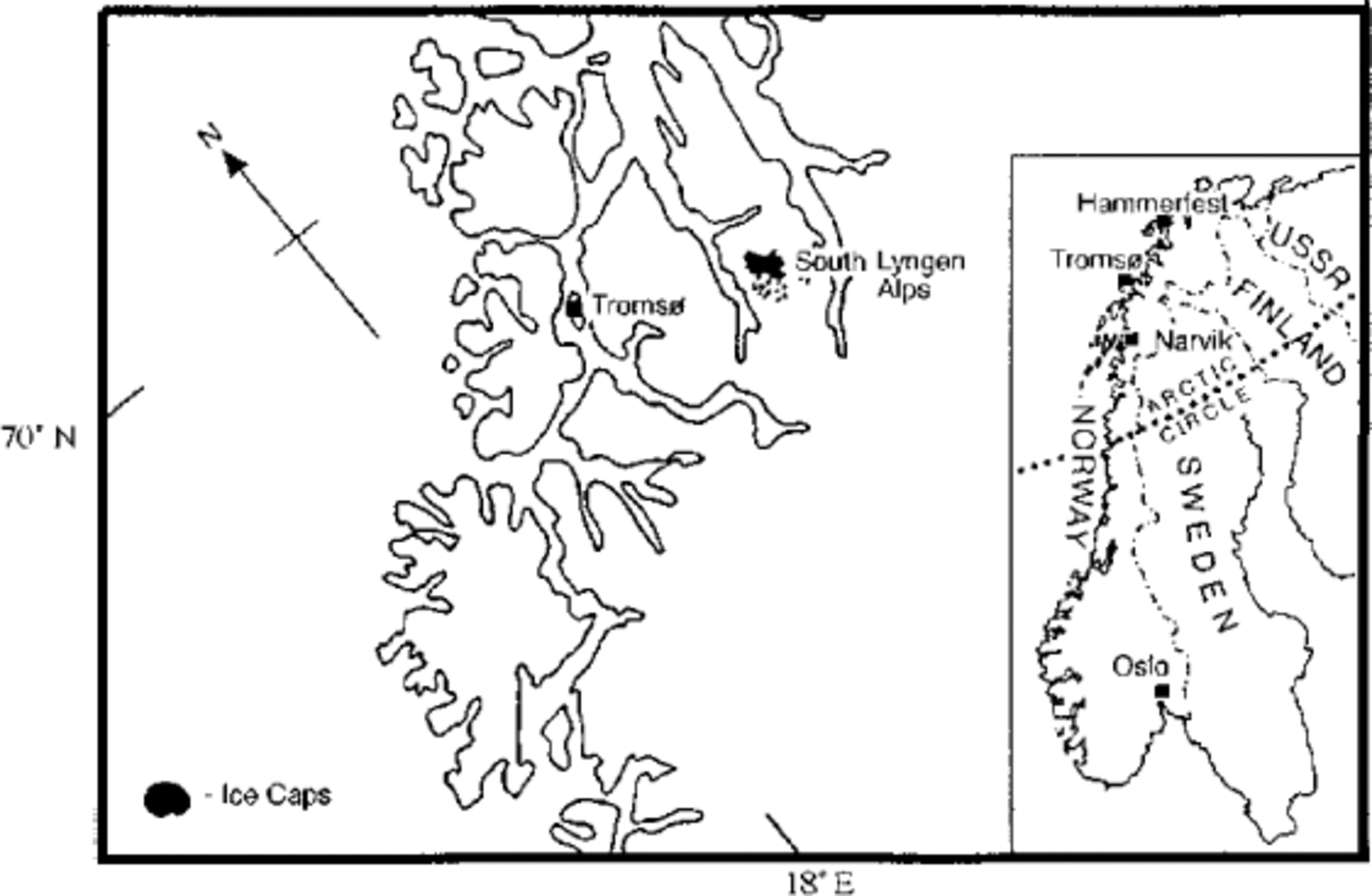
Fig. 1. Location map of the Lyngen Peninsula, North Norway.

The sustaining effect of plateau icefields in maintaining valley glaciers entirely below the regional firn line is highlighted and the possible effect on glacier expansion given a favourable climate change. This paper emphasizes the need to make observations in contemporary glacierized landscapes in order to correctly interpret the style of glaciation in formerly glaciated landscapes.

Study Area

Jiehkkevárri, at 1833 m, is the highest summit in the maritime Lyngen Alps. It rises at the head of Lyngsdalen, an eastward-trending, glacially eroded valley which cuts across the Lyngen peninsula, finally opening into Lyngen Fjord. A core of intensely deformed layered gabbro forms the centre of the peninsula. The gabbro is fault-bounded with the Western Metasediments lying structurally above to the west and the Kjosen Formation lying structurally below to the east (Randall, 1971; Munday, 1974). The summits around Jiehkkevárri are typically plateau with low relief (Fig. 2) and extensive block-field cover (Whalley and others, 1981; Gordon and others, 1987). The block fields are interpreted as relict weathering features of considerable age, pre-dating at least the Weichselian glaciation (Rea and others, 1996). Plateaux above ~1400 m support cold-based icefields resting on block fields (Gordon and others, 1988), their existence controlled by the height of the plateaux above the regional firn line and summit width parallel to the dominant wind direction (Manley, 1955, 1959; Rea and others, 1998). The higher icefields (above ~1500 m) appear to have changed little in extent or thickness over the last 100 years, but the lower icefields and valley glaciers have receded significantly from the position of an early 20th century advance (Gordon and others, 1996). Ballantyne (1990) mapped the “recent” glacial deposits of the area, identifying three age groups of moraines using lichenometry and historical evidence: M1 moraines, AD 1910–20; M2 moraines, undetermined but older than M1 moraines and younger than M3 moraines; M3 moraines, <AD1750 (probably early 18th century, personal communication from C. K. Ballantyne, 1998). The well-mapped LIA ice limits (Fig. 3) and the combination of valley glaciers and plateau icefields make this an excellent location for investigating the effect of contributing plateau icefields to glacier ELAs.

Fig. 2. Oblique aerial photograph of the study region (August 1979), showing the plateau centred around Jiehkkevárri (J). Note the plateau-fed headwall area of Sydbreen (S) and Midbreen (M). (F = Fugledalsbreen; V = Vestbreen; NV = Nord Veidalsbreen.)

Fig. 3. Present extent of the glaciers and the “recent” moraines mapped by Ballantyne (1990). (Modified from Ballantyne, 1990.

Methodology

The limits for the LIA maximum were used for the glacier reconstructions (Fig. 3). M3 moraines delimit the LIA maximum for all the large valley glaciers. A number of other smaller unnamed glaciers and Nord Veidalsbreen, which received input from plateau sources, are also included (glaciers 1–5, Fig. 4). The moraines of these smaller unnamed glaciers are assumed to be of the M1 group (Ballantyne, 1990). This highlights an interesting characteristic of the LIA limits in the area, i.e. M3 moraines delimit the LIA maximum for larger valley glaciers, while M1 moraines delimit the LIA maximum for the smaller glaciers (Ballantyne, 1990). However, the differences in areal extent between the two (i.e. M1 and M3) are, for our purposes, negligible. Thus, the LIA maximum valley glaciers were reconstructed from the morainal evidence. Plateau icefields left no morainal evidence at their LIA maximum (Whalley and others, 1996). At present, ice has receded from the plateau edge in only a few areas. For such areas, the LIA extent was estimated and in all instances was extended to the plateau edge (this has no significant effect on the subsequent areal calculations). Ice divides were defined for the plateau icefields using the present ice divides deduced from the most recent 1: 50 000 topographic maps (1987 field checked). Drainage directions from the plateau icefields, and which valley glaciers they would feed, were similarly established. Figure 4 shows the reconstructed valley glaciers and plateau icefields, ice divides and ice-flow directions. The total glacierized area is ~50 km2, with approximately 25% of this plateau ice. From this information (i.e. valley-glacier and plateau-icefield areas and altitudes, and morainal limits) it is possible to calculate ELAs using a number of techniques. These are outlined in the following sections.

Fig. 4. Reconstructed ice limits and ice-flow directions for plateau icefields and valley glaciers in the study area at the LIA maximum.

Accumulation area ratio (AAR)

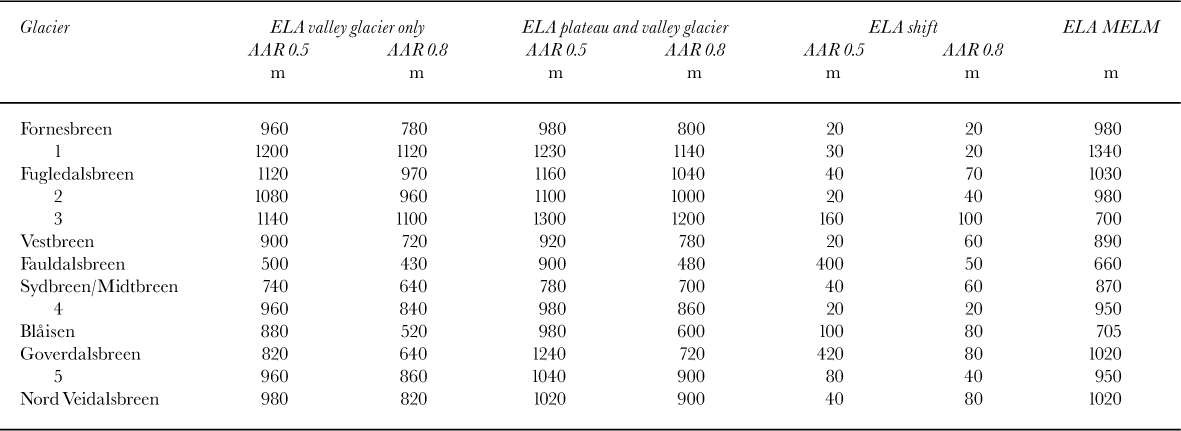
The AAR method is based on the assumption that there is a steady-state relationship between the accumulation area and total area of a glacier. Based on work on temperate glaciers by several authors, the accepted values for glaciers in equilibrium range from 0.5–0.8 (Meier and Post, 1962; Porter, 1975; Kuhle, 1988). A ratio lower than this implies that glaciers are retreating; higher, that they are advancing. This method is generally considered the best for determining glacier ELAs (Hawkins, 1985; Nesje, 1992; Torsnes and others, 1993). However, there could be marked differences in calculated ELAs if the AAR method is used for a valley glacier when there is also mass contribution from plateaux above. Area measurements were made from an enlarged version of Figure 4 (which included glacier-surface contours), using a Planix 7 digital planimeter (resolution 10 mm²). Measurements were made at 1:1 scale, then converted to map scale and averaged over three readings. Table 1 shows the ELAs calculated using AARs of both 0.5 and 0.8 for valley glaciers alone, and combined plateau-valley glaciers. Note the altitudinal shifts in ELAs when plateau accumulation areas are included in the calculations. A few notable examples are Fauldalsbreen and Goverdalsbreen, using a 0.5 AAR where the ELAs shift by 400 m and 420 m respectively. These very substantial shifts are caused by the retreat up-glacier of the ELA beyond the limits of the “valley glacier”. A similar effect is noted for glacier 3, using an AAR of 0.5.

Table 1. ELAs for the plateau icefields and valley glaciers in the study area during the LIA maximum, calculated using AAR (for both valley glacier and plateau icefield contribution) and MELM.

Toe-to-headwall altitude ratio (THAR)

This is a simple method used for rapidly calculating the ELA of a glacier or palaeo-glacier (Meierding, 1982). It is based on the ratio of the altitudinal range of the glacier i.e.

(1)

where ΔH is headwall altitude—snout altitude, c has a range from 0.35–0.45 and h _s is snout altitude.

Although useful for quick estimates of ELAs, this method suffers from major constraints as it takes no account of glacier morphometry and has problems when applied to plateau-valley glacier systems. For example, a THAR calculation for a glacier with a “wide” accumulation area spanning a low altitudinal range with a “long narrow” ablation zone, would produce too low an ELA. If THAR calculations use only the valley headwall altitude then, with regard to plateau-valley glacier systems, they will underestimate the ELA. And if the plateau ice divide is taken as the “headwall” altitude, then an overestimation would likely result. For example, taking only the valley glacier Fornesbreen, the THAR method produces ELA estimates of 613–703 m. If the summit altitude of the plateau ice (1680 m) is taken as the “head- wall” altitude, the ELA estimates of 781–919 m are obtained, which is a shift of 168–216 m. When compared to the shift using the AAR method, plateau inclusion adds 20 m to the calculated ELAs, a more realistic value considering it accounts for <5% of the total glacier area. For this reason, THAR has not been used to calculate any ELAs.

Maximum elevation of lateral moraines (MELM)

This method relies on the fact that ice flow in the accumulation zone of a glacier is downward and inward towards the centre, while in the ablation zone it is upward and outward towards the margins. Thus, moraines should only form below the ELA where material is deposited. This method provides the minimum altitude for the ELA, due to the low preservation potential of the upper part of the lateral moraines (the lateral moraines immediately below the ELA are likely to be small and on steep unstable slopes) and also uncertainty regarding the absolute location where deposition began (low debris concentrations could mean that a recognizable moraine forms some distance below the ELA) (Whalley and others, 1996). The MELMs were estimated from Figure 3. Table 1 shows the range of ELAs found.

Interpretation

The AAR and MELM provide the best methods for accurately reconstructing ELAs for the glaciers. As has been noted above, ignoring contributing plateau areas can have a significant effect on the reconstructed ELAs, especially when plat- eau/x add a large percentage to the glacier area. Comparison of the reconstructed ELAs, using both AAR (including plateaux) and MELM methods, shows there is overlap in all but four cases (with one of these being 20 m outside the AAR range). Despite potential inaccuracies in estimating the MELM, it does have the added advantage of providing tangible evidence of the glacier ablation zone. Thus, to find it within the reconstructed AAR range is encouraging.

With respect to glacier mass balance, the effect of a contributing plateau area to a valley/outlet glacier depends on two factors: the percentage area the contributing plateau adds; and the height of the contributing plateau and valley glacier above and below the regional firn line/ELA. The larger the plateau, the higher the ELA for the combined plateau- and valley-glacier system. This relationship is borne out by the values in Table 1. A simple relationship cannot be established; i.e. for a given percentage area of contributing plateau there is not a linear ELA shift, due to the effect of other factors. For example, Fauldalsbreen and Goverdalsbreen both undergo major ELA shifts for an AAR of 0.5 (?400 m) because the ELA rises above the “valley glacier” and up the steep icefalls leading down from the plateau. There is also an effect of the altitudinal drop between the plateau and valley head; i.e. the lower the valley head, the lower the valley glacier will extend and the higher the plateau, the longer it will have a positive mass balance and thus the longer it can sustain the valley glacier. This introduces the concept of the sustaining effect of plateau glaciers, which is a function of their area and altitude above the local firn line.

Sustaining Effect of Plateau/X Contributing Areas

At the simplest level, if a plateau glacier lies above the 100 regional firn line, it has positive mass balance and will feed ice to valleys below, provided it extends to the plateau edge, producing a sustaining effect. Given this situation, a plateau could sustain a valley glacier which lies entirely below the ELA (Gellatly and others, 1986), e.g. Fauldalsbreen and Goverdalsbreen for an AAR of 0.5. However, the values shown in Table 1 relate to the LIA situation. The present “health” of the glaciers around Jiehkkevárri provide further insight into the sustaining effect of plateaux. Fauldalsbreen and Goverdalsbreen both have large contributing plateau areas. The snout altitudes have retreated only 100 m and 60 m, respectively, up-valley from the LIA maximum positions, despite the fact that the valley parts of both these glaciers lie entirely below the present regional firn line (?1000 m a.s.l). Any loss of contributing area has been minimal and of little significance. Also, the eastward-flowing glaciers of Sydbreen/Midtbreen (now separated) and Vestbreen, having had some of the lowest altitude LIA snout positions, are still found at low altitudes (480 m and 580 m, respectively), sustained by ice avalanching from above. Indeed, in the study most of the valley-glacier parts presently lie below the regional firn line (?1000 m a.s.l). Catastrophic decay of these glaciers should have occurred, but this has not happened due to the sustaining effect of ice mass from contributing plateaux. Valley-glacier parts will continue to retreat until equilibrium is reached. However, if the firn line continues to rise, then the narrow plateau summits will become more marginal (Manley, 1955, 1959; Rea and others, 1998) and, once they begin to retreat from plateau edges, the valley-glacier parts should undergo catastrophic decay (Whalley and others, 1996).

Perhaps the best way to imagine the situation is to assume that two mass-balance units exist for the two parts of the plateau-valley glacier system, where they are totally separate and mass is transferred by avalanching. Mass is transferred extra-glacially and the altitude at which the valley glacier exists is governed by the altitude of the valley head. The extension down-valley is then controlled in the normal manner by the ablation gradient on the valley glacier and the accumulation gradient supplied by the plateau, i.e. the mass- balance gradient of the system. If the ELA rises towards the plateau edge, the valley glacier will retreat mainly due to increasing ablation, but also to a decrease in accumulation. Once the ELA rises beyond the plateau edge, input to the valley glacier will decrease rapidly (Whalley and others, 1996). Complete cessation of supply occurs once the ice recedes from the plateau edge. Conversely, on climate cooling there will be a slight increase in accumulation and decease in ablation, producing an advance. Initially, the magnitude of the advance will be controlled by the increase in output from the plateau and later, with increasing significance, will come the decrease in ablation on the valley glacier. When either of the two systems connect and produce a greater accumulation area, and/or the ELA drops below the head of the valley glacier, a glacier advance occurs which is much more rapid than if the valley glacier had not existed.

The sustaining effect of plateau contributing areas means that “valley glaciers” and their geomorphic signature can be found at altitudes lower than would otherwise be the case. Thus, for climate reconstructions based on this evidence, contributing areas must be included where they existed. It should also be recognised that “valley glaciers””, sustained by contributing plateaux during marginal periods, can then react much more rapidly to climate changes favourable for glacier expansion, e.g. increased winter precipitation or decreased annual temperature.

Implications for Climate Interpretations

The data in Table 1 show how ELAs could be underestimated if contributing plateau areas are ignored. For the reconstructed LIA maximum of the glaciers around Jiehkkevárri, ELAs could be underestimated by up to 420 m, depending upon the glacier morphometry. What could these errors mean in terms of climate reconstructions?

Simplistically, two climatic factors control glacier mass balance: winter snowfall A (accumulation) and summer temperature t (ablation) (Liestøl, 1967; Nesje, 1989). Ballantyne (1990) uses a regression to express the relationship:

(2)

Both Ballantyne (1990) and Dahl and Nesje (1992) use Equation (2) to describe the climatic implications of ELA shifts. The relationship in Equation (2) defines the precipitation required to maintain the ELA at a given temperature and vice versa. Taking Equation (2), it is possible then to predict the changes in A and t represented by ELA shifts calculated for the glaciers in Table 1. Contributing plateau areas shift the ELA of the system up-glacier and thus t declines, producing a non-linear decrease in A. Using the 1949–86 temperature— precipitation averages, Ballantyne (1990) used Equation (2) to calculate the temperature—precipitation figures for the M3 moraine formation (early 18th century), based on valley- glacier reconstructions only. The mean summer-temperature depression was estimated to be 1.4°C (assuming a lapse rate of 0.5°C/100m) based on work from Matthews (1977), and the mean winter precipitation ≤525 mm. Averaging the ELA shifts for all the glaciers with M3 moraines, for the maximum and minimum AAR ratios (0.5 and 0.8), gives values of approximately 150 m and 60 m. Thus, t decreases by between 0.75°C and 0.3°C (based on a lapse rate of 0.5°C/100 m). Substituting these into Equation (2) gives mean winter-precipitation values of 404 mm and 470 mm. Such differences are certainly significant and indicate that the recognition of contributing plateaux is important with respect to climate reconstructions.

In southwestern Norway, Dahl and Nesje (1992) and Aa (1996) have both highlighted the potential effect of plateau glaciers on the ELAs of cirques and outlet glaciers due to snow-blow effects. Dahl and Nesje (1992) found a leeward depression of ELAs of 335 m in inner Nordfjord, and Aa (1996) found a leeward depression of 85 m for Grovabreen. Looking at the situation of the glaciers centred around Jiehkkevárri during the M3 event, there appears to have been little ELA depression associated with the plateaux. The prevailing wind direction is southwest and thus glaciers to the north and east would be expected to have depressed ELAs. This does not appear to be the case. The likely explanation is that the drainage of the plateau ice appears to be strongly controlled by bed topography and the main ice divide appears fairly evenly split west and east. The eastward-draining ice, however, supplies only three drainage basins, Vestbreen and Sydbreen/Midtbreen. Thus, the eastward-draining glaciers tend to be larger than the westward-draining ones. This lack of leeward ELA depression further highlights the difficulties in estimating the complex interaction of climate parameters (temperature, precipitation and wind) and topography in controlling the ELAs and dynamics of glaciers.

Discussion and Further Work

In order to interpret a glaciated landscape correctly, it is necessary to recognize the style of glaciation which it underwent during a particular period of time. This is critical in order to avoid underestimations of ice coverage and ice duration in the landscape, leading to erroneous ELA reconstructions and incorrect interpretations of glacier response to climate changes. For example, as highlighted above, the extent of ice coverage could be underestimated resulting in erroneously low reconstructed ELAs and incorrect summer- temperature and winter-precipitation estimates. In glaciated landscapes where valley glaciers have produced moraines, their extent is relatively easy to establish if alpine-style glaciation has occurred. However, if plateaux exist, they must be evaluated in order to establish if they contributed ice mass to the valley glaciers. This can be accomplished using geomorphic evidence and an altitude—area relationship established by Manley (1955, 1959) and extended by Rea and others (1998). The sustaining effect of contributing plateau ice can facilitate the existence and extension of valley glaciers to lower altitudes than in an alpine-style glaciation. Also, the response of the glacier system to climate change is affected by contributing plateau ice, speeding up for climate deterioration and slowing down for climate amelioration. Thus, understanding the glaciated landscape requires investigations in, and understanding of, the glacierized landscape.

One major source of error in ELA estimations using the AAR method is simply the fact that it is an area-based method. It assumes that areas are sufficient because volumes will scale similarly, i.e. the glacier thins snout-ward and head-ward. Making this assumption for a plateau icefield may introduce errors, as it is likely to have a more uniform thickness from ice divide to plateau edge. Thus, at least volumetric calculations for plateau icefields would be better, and complete volumetric mass balances for the whole plateau and valley-glacier systems would be better still (which is the next aim of this research). The influence of contributing plateau areas is important in understanding the response of the valley glaciers to climate change, especially over short periods, and may go some way to explaining anomalies such as the M3—M1 dichotomy for the glaciers in this region found by Ballantyne (1990). While ice-mass contribution from plateaux is obvious in a glacierized landscape, it is often overlooked in reconstructing former glaciers and their ELAs. Thus, areas such as North Norway may provide useful analogues for understanding deglaciated landscapes, e.g. the Cairngorm Mountains in Scotland.

Conclusions

By calculating the ELAs for the glaciers centred on Jiehkkevárri, we have shown that the impact of contributing plateau icefields on valley glacier ELAs can be significant. In some instances, where the valley glacier and contributing plateau are of similar size, the ELA may exist halfway up the mountain side between the two. Normally, an interpretation of such valley glaciers would have to appeal to some topographic and/or anomalous accumulation pattern to account for its low altitudinal situation (e.g. Sissons (1980) for the Lake District, England). In less conspicuous situations, ELAs can be relocated substantially higher up-glacier. Such up-glacier shifts require reinterpretations of the climatic parameters controlling the ELA, i.e. the mean summer temperature t and mean winter precipitation A. Further work is thus required to establish the relationships between contributing plateau areas and associated valley glaciers, to ensure that climate reconstructions based on inferred ELAs in formerly glaciated landscapes take account of these links.