Photogrammetric reconstruction of glacier mass balance using a kinematic ice-flow model: a 20 year time series on Grubengletscher, Swiss Alps

Abstract

The kinematic boundary condition at the glacier surface can be used to provide glacier mass balance at individual points if changes in surface elevation, horizontal and vertical surface velocities and surface slope are known. Vertical ice velocity can in turn be estimated from basal slope, basal ice velocity and surface strain. This relation is applied to reconstruct a 20 year mass-balance curve of Grubengletscher, Swiss Alps, largely using repeated aerial photogrammetry, with only a minimum of fieldwork For individual years the mass-balance distribution on the glacier tongue was modelled with an accuracy of about ±0.9 m a"¹. Ice-mechanical assumptions and errors in glacier bed geometry markedly affect discrete mass-balance patterns but are largely eliminated in the calculation of year-to-year mass-balance changes The resulting 1973–92 curve for the Grubengletscher tongue shows reasonable consistency with meteorological data and other glaciologically derived mass-balance series. Large changes in measured ice speed on the glacier tongue (±50%) significantly governed the long-term variability of ice thickness over the observational period.

Introduction

Investigating glacier mass balance is one of the main research activities in glaciology. Measuring mass balance helps with the detection of climate variations, contributes to the understanding and modelling of glacier reaction and assists hydrological applications and hazard assessment, to mention only some issues. The traditional way of measuring glacier mass balance is by means of scattered, ˚representative" in situ samples (mostly using stakes), an often time-consuming and expensive method, yet one which gives no area-wide mass-balance distribution but requires spatial interpolation. Additionally, conventional mass-balance measurements are difficult on debris-covered ice and in icefalls. These facts render the monitoring of time series of mass balance markedly more difficult. Consquently, longer mass-balance curves are available for only a limited number of glaciers (Haeberli and others, 1999b). Several approaches to direct mass-balance determination have been tested in an attempt to overcome these difficulties. Reynaud and others (1986) used transverse velocity profiles and measured elevation changes to calculate the mass balance of longitudinal glacier sections. Rasmussen (1988) obtained both bed topography and mass-balance distribution iteratively, using repeated aerophotogrammetric measurements of elevation and displacements on Columbia Glacier, Alaska. An approach similar to that presented here is developed by Reeh and others (1999) in order to analyze and process surface velocity data obtained from satellite interferometric synthetic-aperture radar. In our contribution, we apply a remote-sensing-based method, which was developed by Kääb (1996) and is also explained in detail by Kääb and others (1998) and Kääb and Funk (1999). Kääb and Funk (1999) used the kinematic boundary condition at the glacier surface to calculate the mass-balance distribution for a single year on Griesgletscher, Swiss Alps. Due to model-inherent sensitivities and photogrammetric restrictions, the model was tested only for the flat ablation area, but gave a promising accuracy of ±0.7 ma^–1 for individual mass-balance values. (For a similar application, cf Gudmundsson and Bauder, 1999). In the study presented here, we (1) apply the method on the more complex ablation area of Grubengletscher, Swiss Alps, and (2) extend it to a 20 year time series of annual mass balances, each step with no field measurements necessary over the observational period. After a site description, we explain the two model steps of our approach and the methods used to obtain the input data, and then discuss the results of the single steps.

Site Description

Grubengletscher, 1.4 km² in area and approximately 3 km long, is located in the Saas valley, Valais. The highest point of the accumulation area is the Fletschhorn (3993 ma.s.L). The partially debris-covered tongue reaching down to about 2770 ma.s.l. is situated near a conspicuous rock glacier, two cirque glaciers formerly connected to the main glacier, and a number of periglacial lakes (Fig. 1; cf. Kääb and others, 1997). In 1968 and 1970, outburst floods from an ice-dammed lake and subsequent debris flows caused heavy damage to the nearby village of Saas Balen (Rothlisberger, 1979). Since then, a number of investigations have been undertaken, mostly designed to enable early recognition of lake outbursts, and to facilitate protection measures (Kääb, 1996; Kääb and others, 1997; Haeberli and others, 1999a). Many data and insights resulting from these works have been important for our study. Most essential, however, is high-precision aerial photography of the glacier tongue, which has been carried out by the Swiss Federal Office of Cadastral Surveys almost every autumn since 1970 (flying-height about 1000 m; image scale about 1:7000; Kääb and others, 1997). Other photographs covering the entire glacier are available for perennial intervals from the Swiss Federal Office of Cadastral Surveys and the Swiss Federal Office of Topography.

Fig. 1. Spatial pattern of elevation changes on Grubengletscher for the periods 1975–85 and 1985–91. The strong increase of elevation to the northwest of the tongue indicates a glacier advance by about 50 m. Contour lines in m a.s.l. North direction to the left.

Model and Assumptions

The model we use to reconstruct a mass-balance series of Grubengletscher follows two steps: (1) calculating the mass-balance distribution on the glacier tongue for single years using the kinematic boundary condition at the surface, and (2) deriving a mass-balance series from the single-year mass balances.

Kinematic boundary condition at the surface

The kinematic boundary condition at the glacier surface can be used to provide glacier mass balance at individual points as a function of changes in surface elevation, horizontal and vertical surface velocities and slope. Vertical ice velocity can in turn be estimated from basal slope, basal ice velocity and surface strain. The relation is derived from mass conservation in a vertical column over the entire ice thickness (Hutter, 1983; Paterson, 1994; Kääb, 1996; Kääb and Funk, 1999). We use it in the form

(1)

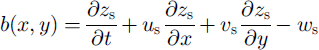
with

(2)

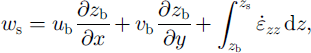
where b is the mass balance at a point (x, y), z_s is the surface elevation, ∂z_s/∂t is the change in surface elevation with time, u_s and v_s, and u_h and v_h, are the horizontal velocity components at the surface and at the glacier bed, respectively, ∂z/∂x and ∂z/∂y are the accordant slope components, ws is the vertical surface velocity, z_h is the bed elevation and is the vertical strain rate.

In our study, we try to determine all terms on the right-hand side of Equations (1) and (2) and, subsequently, to calculate the mass-balance distribution on the glacier tongue point by point. Surface slopes, changes in surface elevation and horizontal surface velocities are derived from repeated photogrammetry Bed topography and ice thickness is obtained from ground-based geophysical soundings (see Methods section below). The basal velocity (sliding and sediment deformation) is estimated by comparing measured surface velocities with a simple flow-law assumption (usual flow-law parameters, a shape factor of 0.8 and surface slope averaged over a distance of about ten times the ice thickness) and applying the simple relation

(3)

(analogous for v_b). We obtained a general ratio of basal velocity to total surface velocity of about 90% (β ≈ 0.9), which varies less than ± 5 % due to temporal ice-thickness changes and uncertainties in the flow-law parameters. This estimation, of course, implies a large inaccuracy with potentially noticeable spatial and temporal variations.

Observed surface velocities of up to 45 m a^–1 (see Results), which are unexpectedly high in respect of the low slope on the glacier tongue, are the expression of this high basal velocity. The following facts are possible causes for this high basal velocity:

Non-frozen sand and silts with a thickness of 100 m and more exist beneath the glacier tongue and could allow for high sediment-deformation rates (Haeberli and Fisch, 1984; cf Haeberli, 1981).

Observations in an ice tunnel near the ice-dammed lake (Haeberli, 1976; cf. Röthlisberger, 1979) and on the glacier surface (see Mass-balance distribution) provide indications of intraglacial shearing.

From fieldwork in the 1970s, the tongue is known to have been partially frozen to its bed at the margins (Haeberli, 1976). This marginal sealing led to high subglacial water pressure, expressing itself in artesian water sourcing from boreholes. The latter could not be observed on a second drilling campaign in the mid-1990s.

The several hundred metres long tongue itself is flat ( ω10°), while the adjacent glacier parts are much steeper (25–30°), a precondition which might cause some pushing of the entire ice column additional to deformational stress coupling.

The second estimation which is needed to solve the kinematic boundary condition is the variation of strain rate with depth (cf. Equation (2)). Again we use a very rough approach assuming a linear relation between the total vertical strain at the surface ε_zz , on the one hand, and the ice thickness h and the vertical surface-strain rate ε_zz , on the other hand:

(4)

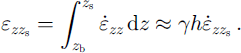
The horizontal surface-strain rates were derived from thevelocity fields using a method proposed by Nye (1959), and the vertical surface-strain rates were obtained from the in-compressibility condition Considering the high ratio of basal velocity a ₇ of 1.0 was introduced (cf Gudmundsson and Bauder, 1999; Kääb and Funk, 1999). As for the estimate of the basal velocity, we presume a potentially large spatial and temporal uncertainty of the latter assumption.

Using the above two ice-mechanical estimations, and photogrammetric and geophysical measurements, it is possible to finally compute the mass-balance distribution on the glacier tongue for a single year, which represents the first step of our model chain towards reconstructing a mass-balance curve. One remaining problem consists in potential errors in the glacier bed determination, especially if the geophysically derived bed topography (e.g. the ice-sediment transition) does not coincide with the ˚kinematic" bed, i.e. the basal horizon used in the kinematic boundary condition (cf. Mass-balance distribution).

Mass-balance variations

Equations (1–4) show that the effect of measurement errors and faulty ice-mechanical assumptions will increase with increasing basal velocity, increasing bed and surface slope and increasing ice thickness and strain rates. Thus, single mass-balance values calculated for Grubengletscher will potentially have a much larger error than, for instance, the planar and slow-flowing tongue of Griesgletscher (Kääb and Funk, 1999). Independently of the valuable conclusions about ice-flow characteristics which can be drawn from such analyses (see Results), we are here more interested in mass-balance variations with time than in the absolute accuracy of individual mass-balance values or in the distribution pattern. In this second step of our model chain, the effects of the uncertainties of our estimations and of measurement errors are reduced in two ways: (a) The reconstruction of the mass-balance series for the glacier tongue requires only one average mass-balance value per year for the tongue. Spatial averaging of each annual mass-balance distribution to one average value will eliminate the error components of high spatial frequency and random noise to some extent. Absolute deviations will nevertheless remain, (b) The mass-balance variation Δ6 for individual points is basically derived from differences of the Equation set (1–4) between two years:

(5)

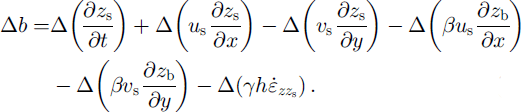
In Equation (5) the first three terms, and the surface velocity and vertical surface-strain rate in the fourth, fifth and last terms, can be directly derived from photogrammetric measurements. A time-constant component of the error in (3 would be eliminated if one assumed both surface velocity and bed slope being constant with time (analogously for an error in bed slope); a time-constant component of the error in 7 would be eliminated if one assumed both strain rates and ice thickness constant with time (analogously for an error in ice thickness). The assumption of constant bed slope will certainly apply to a major extent on a year-to-year time-scale. Surface velocities, strain rates and ice thickness varied by not more than 10% from one year to the next over the observational period. Thus, only errors of second order will remain when calculating annual mass-balance variations and fixing the whole series to its temporal average.

Methods

To solve the kinematic boundary condition Equations (1–4), the annual surface topography and the annual surface velocity field of the Grubengletscher tongue, as well as the glacier bed topography, need to be known. In our study, primarily aerophotogrammetric techniques are used to obtain the above data. Surface slopes and changes in surface elevation (cf. Equation (1)) are derived from a total of 21 digital elevation models (DEMs), each with 25 m regular grid spacing and including about 1000 points. Gaps in this time series (cf. Fig. 11a) are due to missing photography. The height values of the DEMs have an accuracy of about ±0.2 ma^–1 (rms), and the elevation changes an accuracy of about ±0.3 m a"¹.

For seven individual years, irregularly distributed over the observational period, aerial photography of the entire glacier (image scales from 1:11000 to 1:20 000) was available to determine complete DEMs of the glacier and related elevation changes (50 m resolution and about 700 points each DEM). In this contribution, only data of the glacier tongue are used. However, the elevation changes of the entire glacier are also displayed for comparison (cf. Figs 1 and 2).

Fig. 2. Cumulative changes in surface elevation of Grubengletscher and its tongue for the period 1967–95, as derived from repeated aerial photogrammetry. For the glacier tongue a much denser time series of photography and related DEMs (indicated as open circles) are available.

While the DEMs were derived from repeated monotem-poral photogrammetric stereo pairs, the surface velocities were determined by a special procedure simultaneously comparing two aerial photographs taken at different times and from different positions (so-called multitemporal stereo models). The spatial resolution of the obtained velocity fields is similar to that of the DEMs. Due to photogrammetric restrictions (e.g. insufficient optical contrast) and missing photography, a reduced number of 14 velocity fields has been measured. The accuracy of an individual displacement vector, deduced by comparison with stake measurements, is about ±7%, i.e. ±1.7 ma^–1 on average for the Grubengletscher tongue. Various photogrammetrically derived data from Grubengletscher have been determined from 1967 to 1995, whereas a complete overlapping dataset with DEMs and velocity data, as needed for our model, is available only for the period 1973–92. Details on the photogrammetric techniques used, related accuracy and postprocessing procedures are described in Kääb (1996), Kääb and others (1997) and Kääb and Funk (1999). The propagation of photogrammetric errors towards the calculations of vertical ice velocity and mass balance (Equations (1) and (2)) is evaluated in Kääb and Funk (1999).

The bed slope and the ice thickness (cf Equations (2) and (4)) were derived from the glacier bed topography. Haeberli and Fisch (1984) compiled it from radio-echo soundings and hot-water drilling with borehole electrodes, obtaining also valuable information about the subglacial sediment layer (see Model and assumptions, above). In most places the accuracy of the measured ice thickness is about 5%, with possible single errors of about 10% or more. Postprocessing procedures for the ice-thickness data are described in Kääb (1996) and Kääb and Funk (1999).

Results

Surface kinematics

In this subsection we describe and discuss the input data as well as the results of our calculations. Figure 2 depicts the cumulative changes in elevation of Grubengletscher, as derived from DEMs of the entire glacier and the tongue. The spatial distribution of the elevation changes is exemplified for the periods 1975–85–91 (Fig. 1). During 1967–95 Grubengletscher experienced three different major periods of volume change:

From 1967 to 1975 (1976 for the tongue) the average elevation remained nearly constant and the tongue thinned by about –0.2 ma^–1.

During the period from 1975 (1976) to 1985 the glacier became thicker by about +0.25 m a"¹ (+0.5 m a"¹ for the tongue), a development which is known as the ˚1980s maximum" for many other Swiss glaciers and could, in a similar form, also be observed for the nearby Gruben rock glacier (Kääb and others, 1997).

From 1985 to 1991 (1995) the glacier thinned considerably by –0.8 m a"¹ (–0.6 m a"¹ for the tongue).

The elevation changes on the glacier tongue are attenuated by the heavy debris coverage of the lowest part (cf. Fig. 3). Average annual changes on the debris-free part range from +1.5 to 2 m a"¹ for the above periods (approximately ± 5% of the ice thickness per year). The only surface rise during 1985–91 occurred to the northwest (NW) of the tongue where a distinct advance of about 50 m (horizontal distance) during 1975–85 continued over the last period to a reduced extent. Surprisingly, at a first view, the advance did not take place at the terminus close to the moraine lake, but laterally. The advance clearly followed today’s main flow direction (Fig. 4; cf. Kääb and others, 1997).

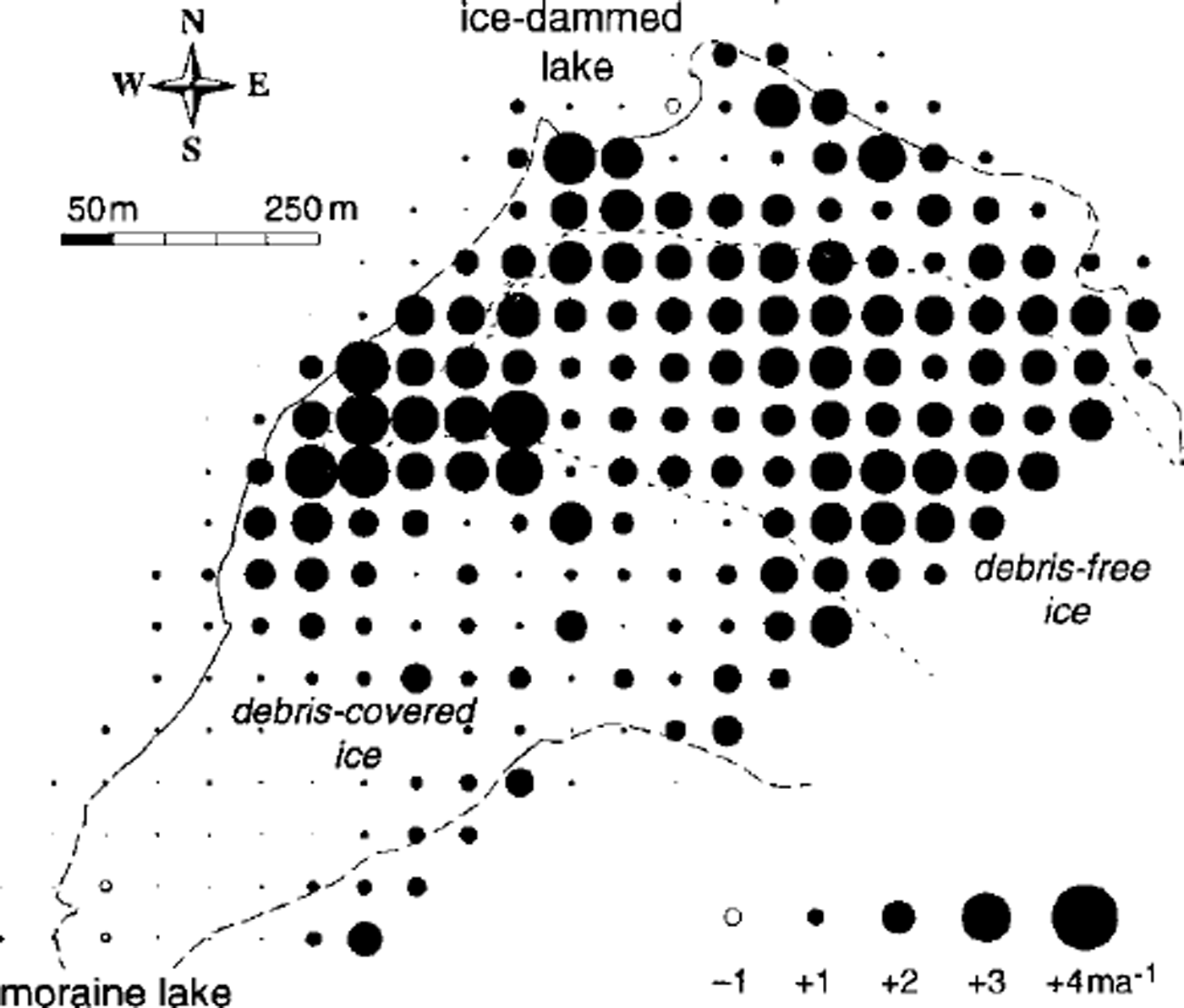
Fig. 3. Annual changes in surface elevation, ∂z_s/∂t, of the glacier tongue for the year 1979/80. The dashed line indicates the boundary of debris cover. North direction upwards.

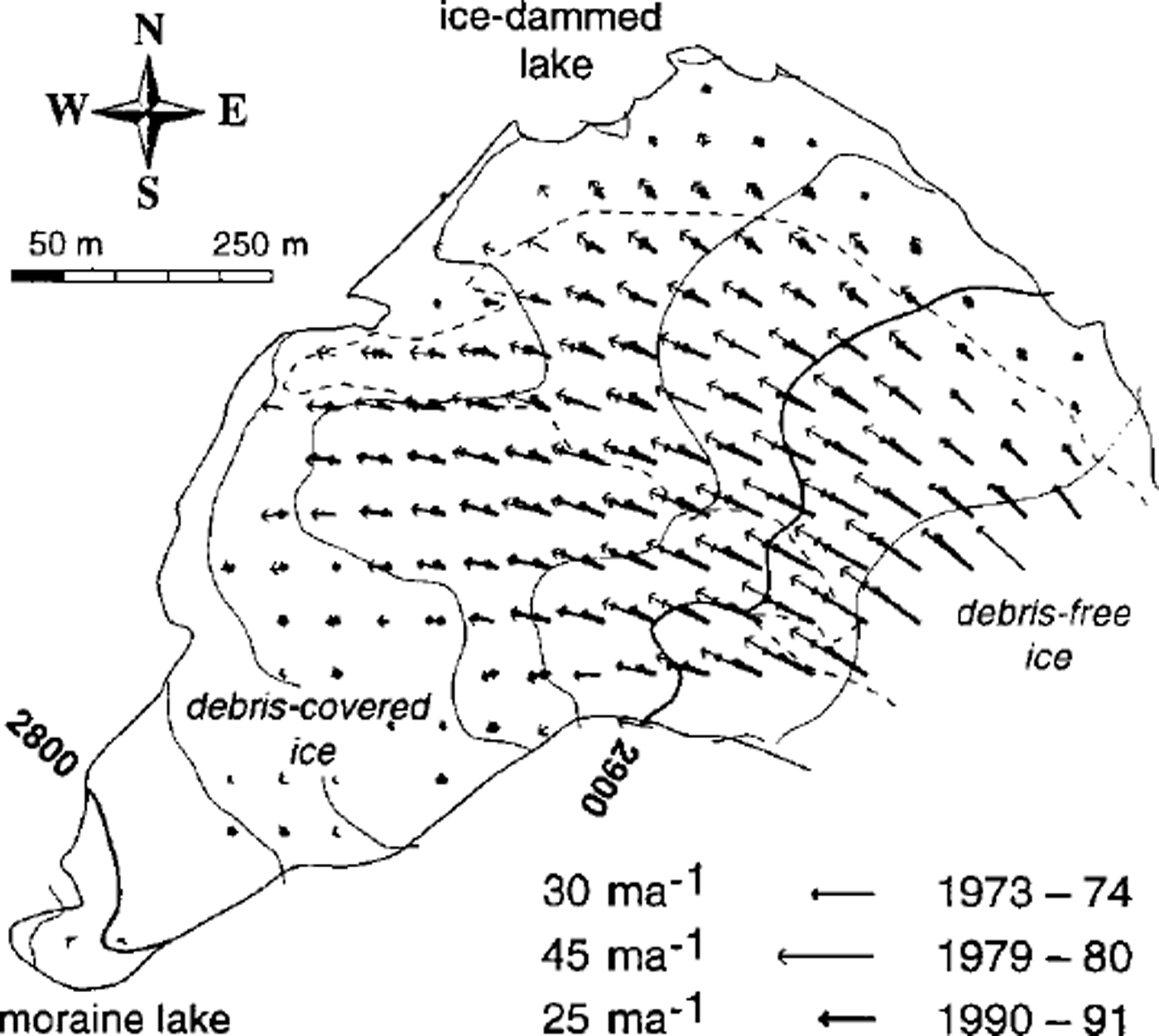
Fig. 4. Annual horizontal velocity fields of the glacier tongue for 1973/74,1979/80 and1991f)2, indicating drastic changes inflow regime (cf. Fig 11a). The velocities quoted represent approximate maximum observed values for each period.

In the following presentation of results, the mass-balance year 1979/80 will serve as an example for our spatial calculations. Figure 3 shows the changes in surface elevation ∂z_s/dt over that period. In 1979/80 the glacier tongue experienced the largest increase of ice thickness over the observational period (cf. Fig. 11a). The raw measurements (25 m spacing) were smoothed (cf. Kääb and Funk, 1999) and are depicted with 50 m spacing. Even so, a smooth pattern for the debris-free ice, and more erratic spatial variations with generally lower elevation changes for the debris-covered ice, can be distinguished.

Figure 4 gives three examples of the 14 determined horizontal velocity fields. Due to photogrammetric and terrain restrictions, measurements were not possible for the complete tongue. The partially scattered data were interpolated to a 50 m grid. As can be seen from Figure 11a showing the horizontal surface speed averaged for the entire tongue, the velocity fields given in Figure 4 represent approximately minimum and maximum stages during the observational period. Maximum speeds observed at individual points are 30ma^–1 in the year 1973/74, 45 ma^–1 in 1979/80 and about 25 m a"¹ in 1991/92. The drastic changes in surface speed (almost 50% in 10 years; Fig. 11a) coincide only very roughly with the development of ice thickness (Fig. 2). The ice speed decreased from the beginning of the 1980s, and the surface elevation from the mid-1980s, which indicates that the variations of speed were not governed by the ice-thickness vanations during the 1970s and 1980s. The latter observation and the estimated high basal velocity (cf. Model and assumptions, above) suggest that some subglacial effect (water pressure?) may be mainly responsible for the velocity changes. The velocity fields show a rather inactive terminus to the southwest (SW), receiving only a minor part of the ice supply which tends to be directed to the NW. Especially from 1973 to 1980, the SW and the northeast (NE) part of the tongue experienced a different temporal behaviour, suggesting that the tongue may be dynamically divided, which might be underlined by the different debris coverage of the

The horizontal and vertical surface-strain rates were calculated from the horizontal velocity fields. Both are exemplified for 1979/80, including the crevasse pattern mapped for 1980 (Figs 5 and 6). Strong longitudinal compression of ≥ 0.1 a"¹ can be found in the SW part compared to markedly smaller values to the NE. A zone of horizontal extension coincides with the observed crevasses with respect to their location and direction. Compressive flow clearly prevails on the Grubengletscher tongue, as generally expected for ablation areas. Some features of extensive flow can be attributed to the topographically induced widening of the flow field.

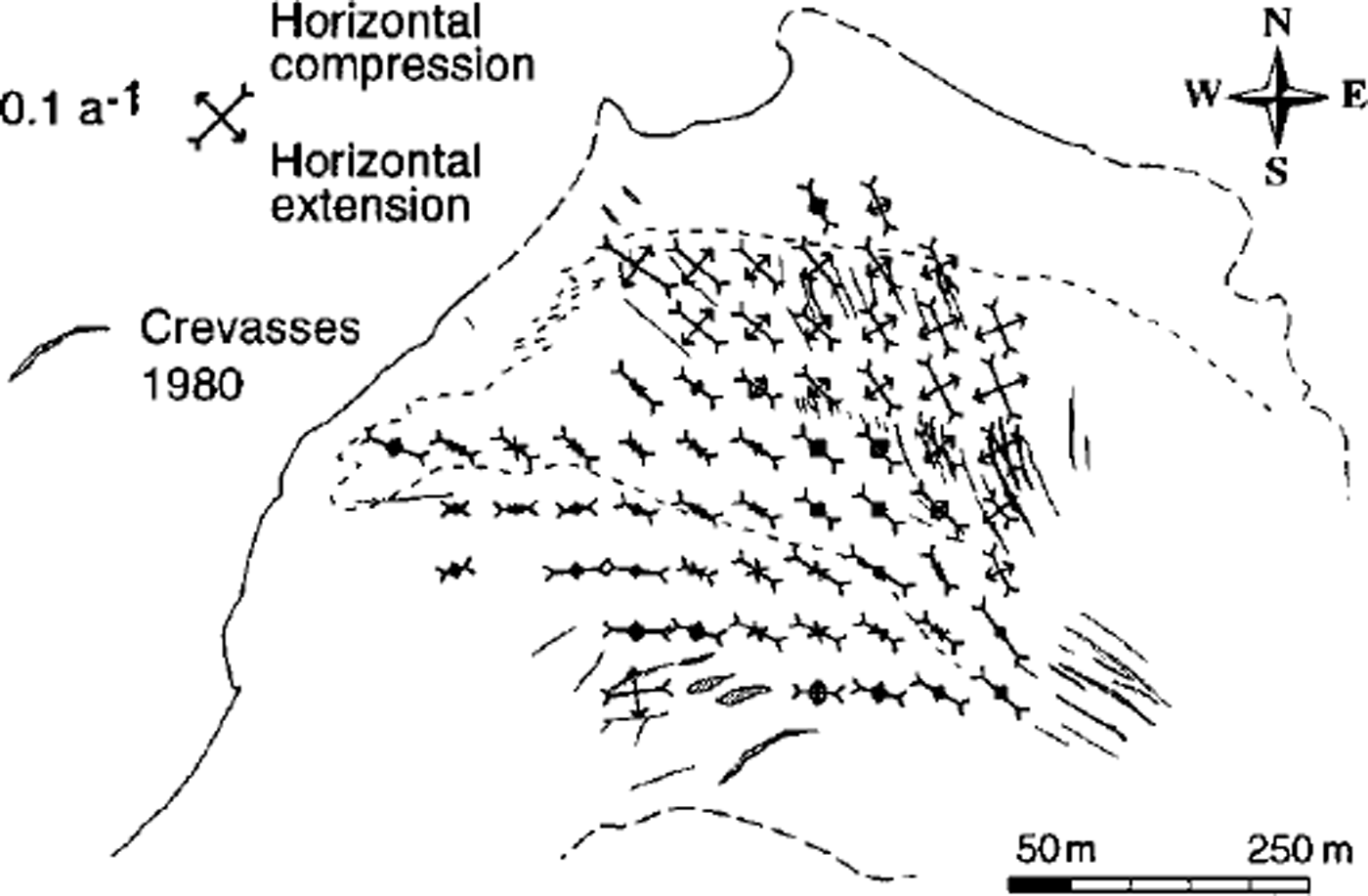
Fig. 5. Horizontal principal surface-strain rates during 1979/ 80 derived from the velocity field. The crevasses of 1980 were mapped photogrammetrically. The dashed line on the tongue indicates the boundary of debris cover (cf Fig 3). The solid and dashed parts, respectively, of the glacier outline represent certain and uncertain identification on the aerial photography. SW and NE parts of the ablation area. Between 1979 and 1992, generally representing a phase of glacier thinning, a small clockwise rotation of flow direction occurred in the NW part of the tongue.

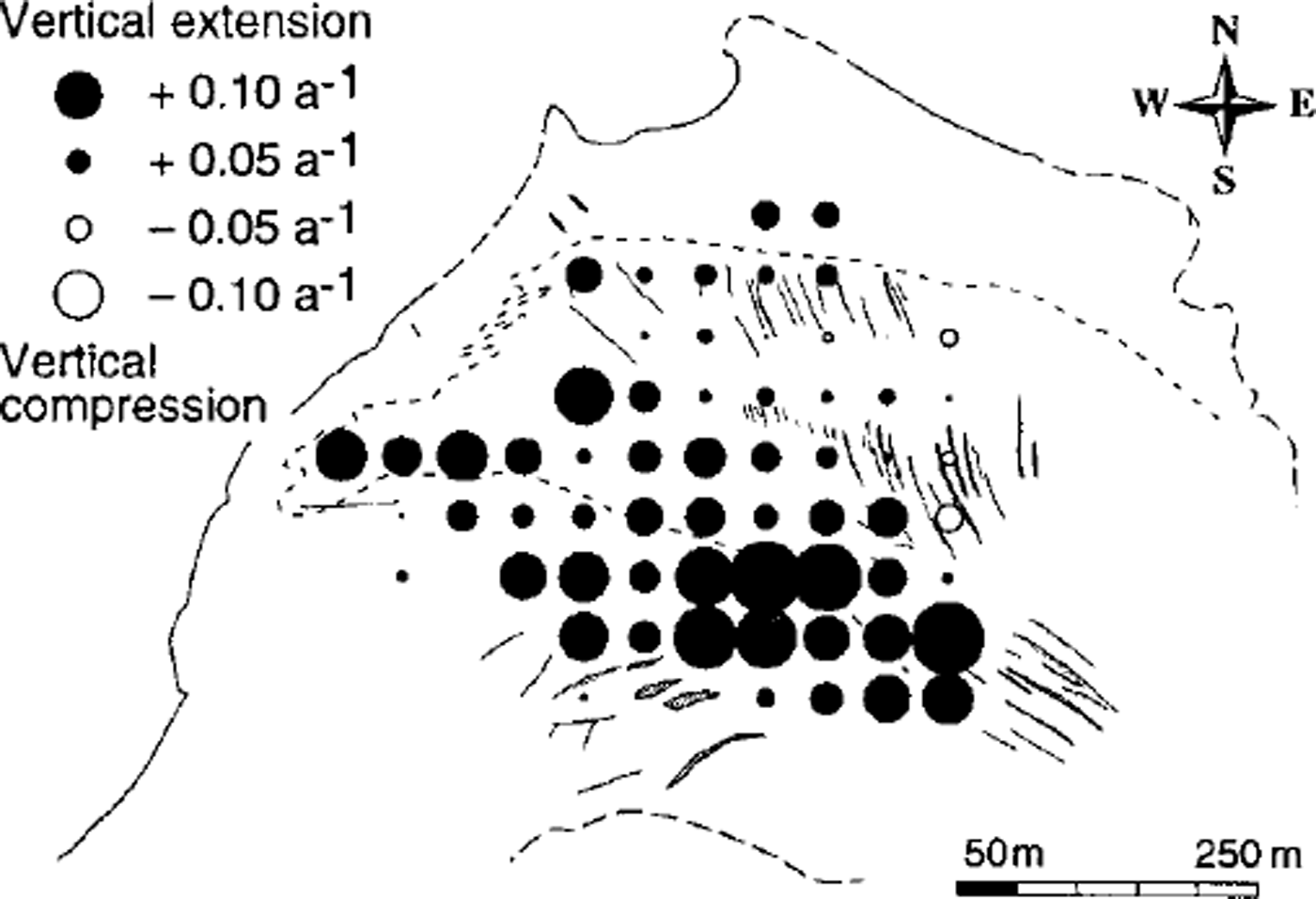
Fig. 6. Vertical surface-strain rates, during 1979/80 calculated from the horizontal strain rates assuming incompressible ice.

Details on the glacier bed topography (Fig. 7), our last missing model input, can be obtained from Haeberli and Fisch (1984). However, it should be pointed out that the direction of the bed trough rotates from the NW direction in the upper part to the SW direction in the lower part, which is not so apparent in the flow field (Fig. 4). An upward flow component towards the ice-dammed lake is the result.

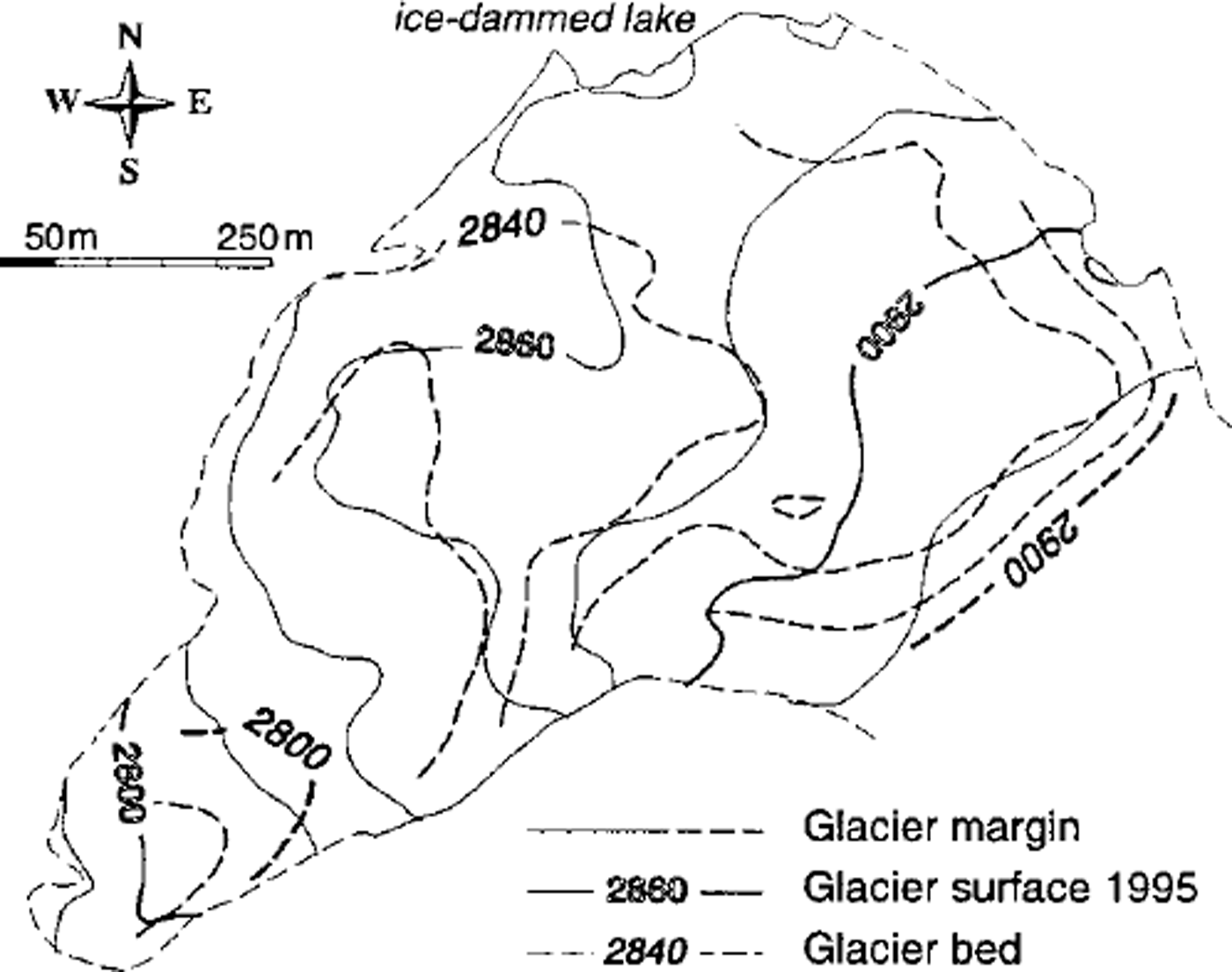
Fig. 7. Contour lines of glacier bed geometry (dashed lines, in ma.s.l) as determined by radio-echo soundings (after Haeberli and Fisch, 1984). Ice thickness of the central parts is 20–60 in in 1995, and up to 15 m more m 1985.

Mass-balance distribution

The distribution patterns of the vertical ice velocity at surface, and the mass balance calculated from Equations (1–4), are illustrated for 1979/80 (Figs 8 and 9). The general pattern of the calculated vertical ice velocity at the surface w_s (Fig. 8), with negative values in the upper part and positive values in the lower part, seems to reflect mainly the bed slope with respect to the flow direction (cf. above discussion of bed topography). The small negative values or even positive values in the SE part are caused by a small plain or bump in the bed data. Model tests showed that the results of w_s are quite sensitive to a smoothing of the bed data affecting particularly this bump.

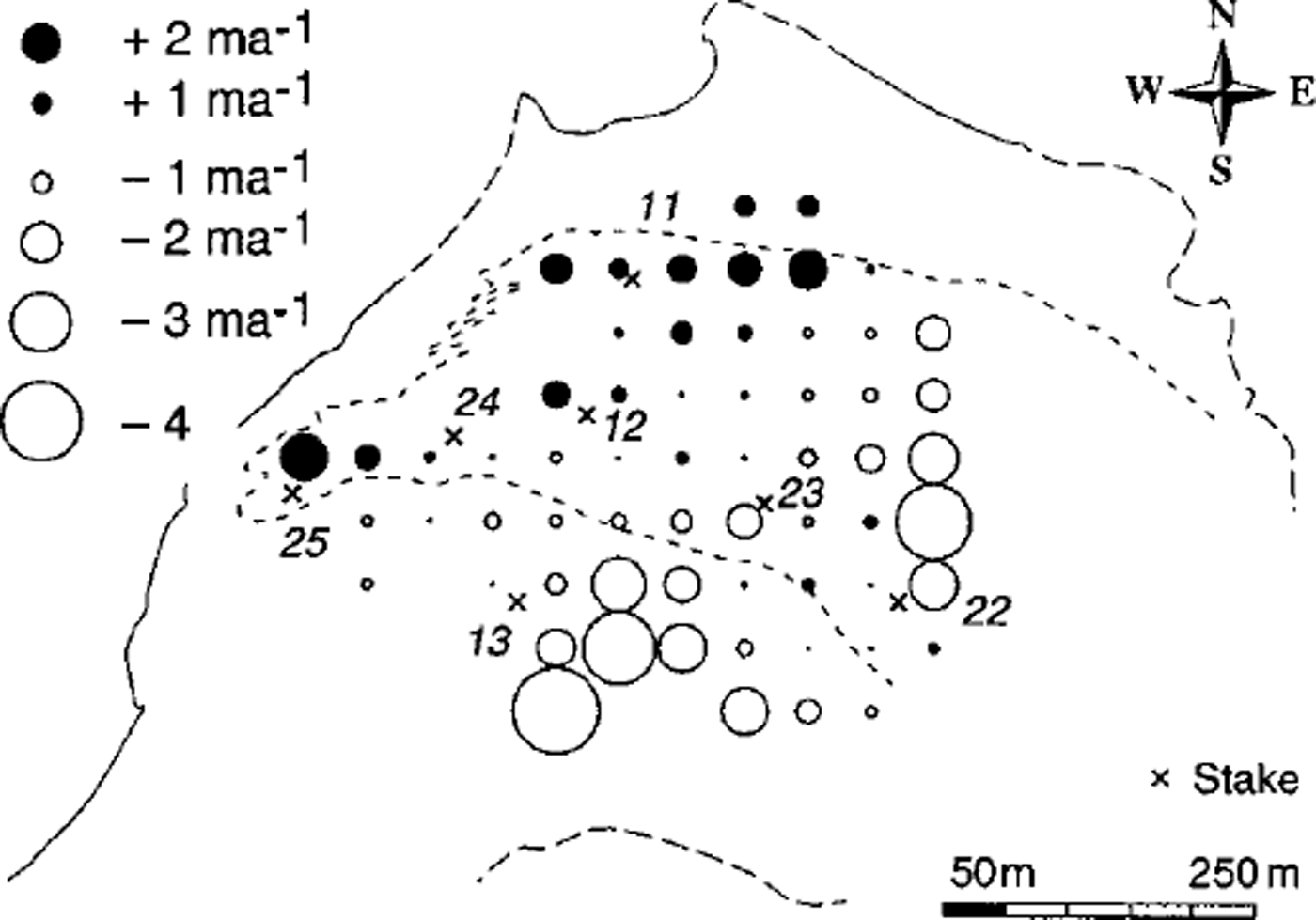
Fig. 8. Calculated vertical ice velocity, ws,for 1979/80 including positions of stakes. The dashed line on the tongue indicates the boundary of debris cover (cf Fig. 3). The solid and dashed parts, respectively, of the glacier outline represent certain and uncertain identification on the aerial photography.

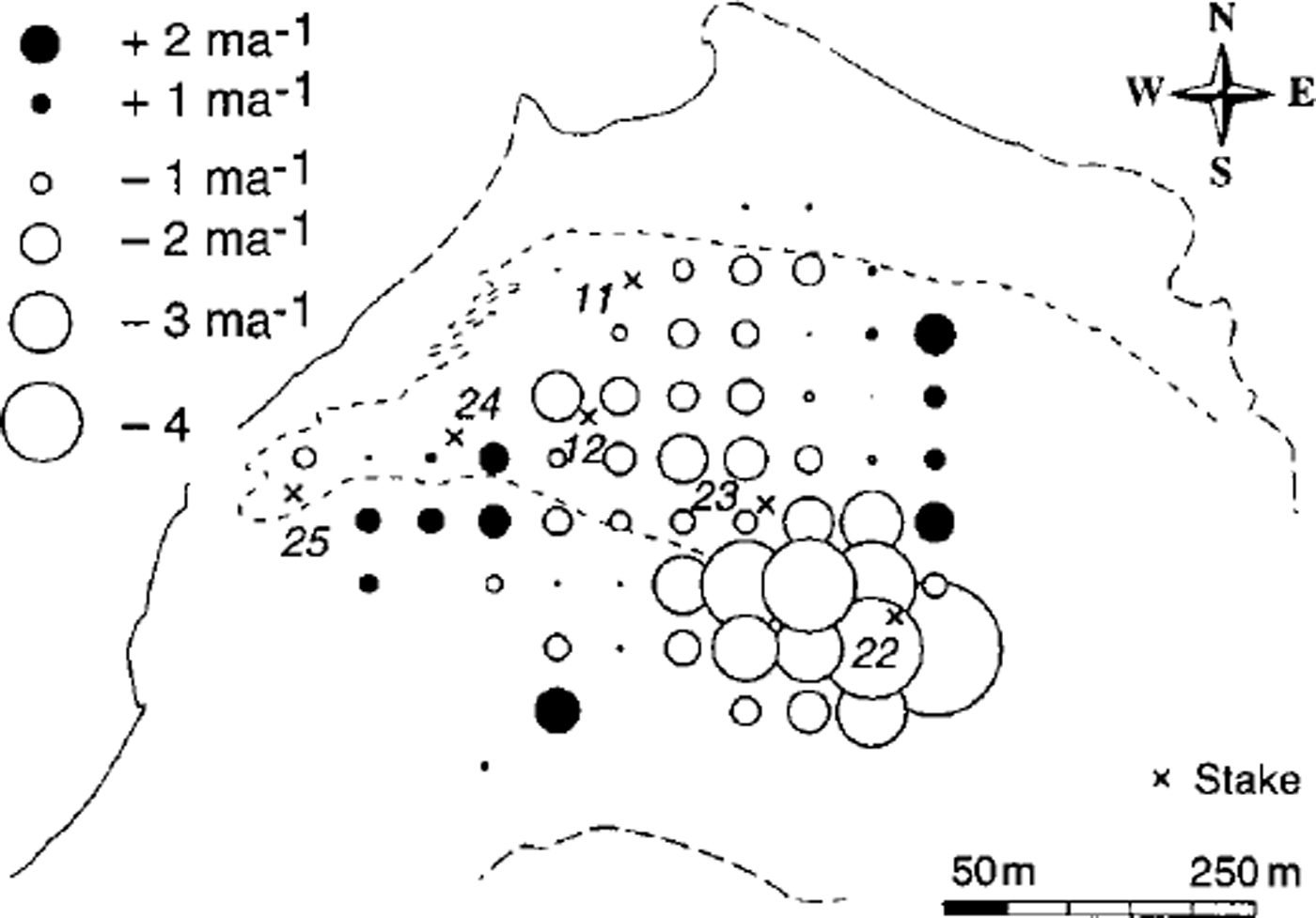
Fig. 9. Calculated mass-balance pattern, b, for 1979/80 including positions of stakes.

The final mass-balance distribution (Fig. 9) is questionable in some parts. While negative values predominate as expected, some positive values are hard to explain. They are more likely attributable to errors in our ice-mechanical assumptions or faulty bed topography than to errors in the photogrammetric data. The small positive values and negative values for the heavily debris-covered ice to the SW make sense, in that an erratic mass-balance distribution highly dependent on the local characteristics of the morainic cover could be expected there. However, the microtopography of this area (large boulders of 2–5 m diameter) markedly complicates the photogrammetric measurements and the model applicability. Surface slopes and elevation changes, derived from 25 m spaced measurement points, could partially be affected by individual boulders not sufficiently representing their surrounding topography. These problems are illustrated by the changes in elevation for 1979/80 (Fig. 3) which show irregular spatial variations for the debris-covered ice. A general dependence of mass balance on elevation can be seen neither from the distribution pattern for 1979/80 nor for other years. This is not surprising in view of the small elevation range of the investigated glacier part and also the large spatial variations of debris coverage and relief parameters (slope, aspect, roughness, etc.) influencing differential ice melt.

For 1979/80 the results can be compared with some geodetic and glaciological stake measurements (Fig. 10). Whilst similar investigations on Griesgletscher, carried out under more favourable conditions with respect to model applicability, gave an accuracy of ±0.3 ma^–1 for the vertical ice velocity at the surface and of ±0.7 m a"¹ for the mass balance (Kääb and Funk, 1999), the results presented here are heavily affected by the assumptions and model sensitivities. Errors in bed slope, A ₇ or ice thickness, for instance, have a large influence on the calculated vertical ice velocity due to the high basal velocity, large strain rates and complex bed geometry (cf. Equations (2–4)). Ignoring stakes 22 and 24, the stake measurements and the calculations of the vertical ice velocity at the surface agree within ±0.6ma^–1 on average. Assigned only to errors in the model parameters β6 and ₇ γ this deviation would on average be equivalent to an error in 0 of ±0.2 or an error in ₇ of ±0.5. Thus, for the Grubengletscher conditions our model is more sensitive to the estimation of the basal-velocity Equation (3) than to that of the vertical-strain-rate-variation Equation (4).

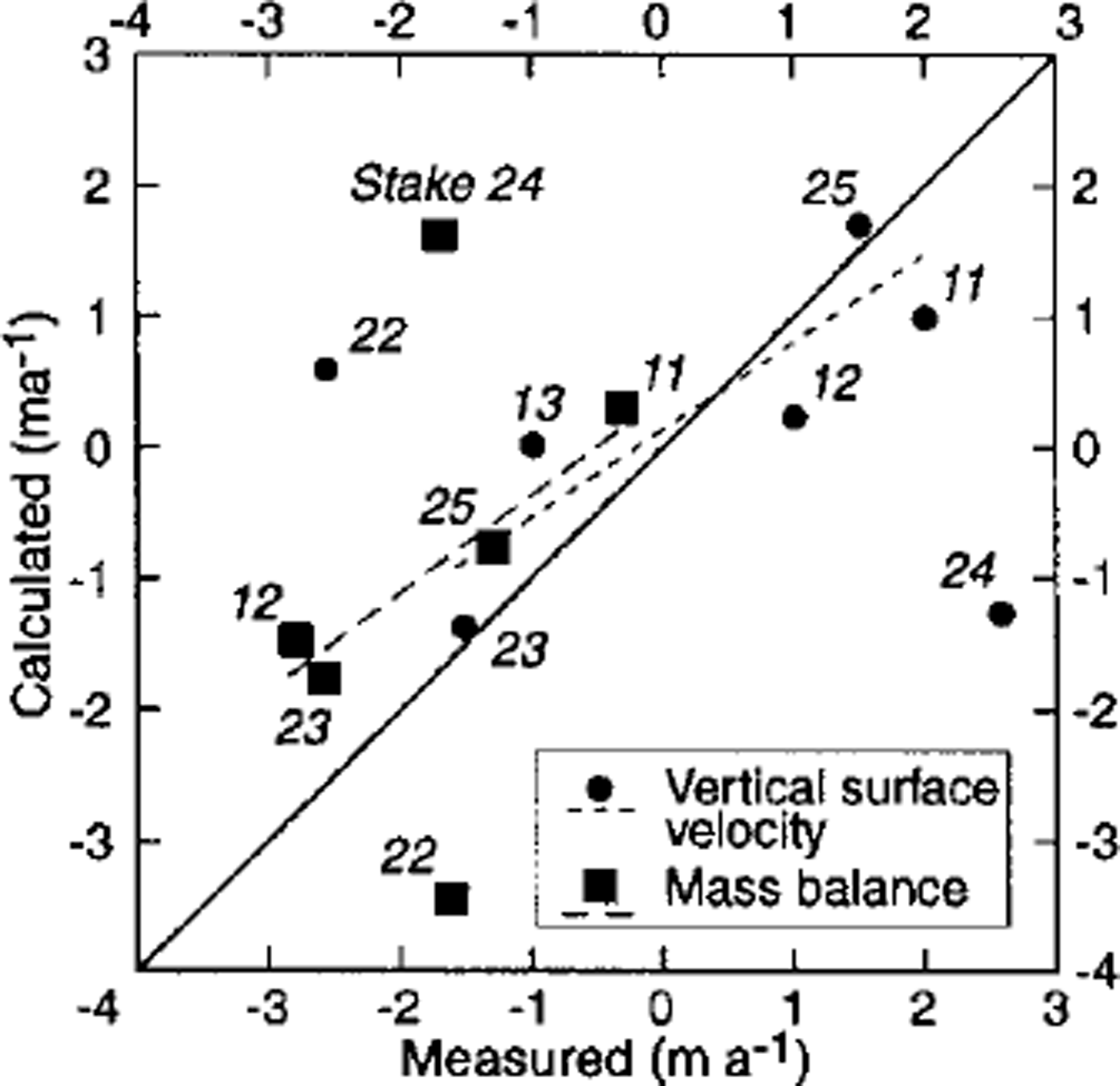
Fig. 10. Comparisons between stake measurements of the vertical ice velocity, w_s, and mass balance, b, and calculated values, both for 1979/80. Mass balance is not available for all stakes. The dashed lines represent linear regressions without stakes 22 and 24 (see text).

We attribute the large deviation for stake 22 to an error in bed topography, which may consist in a difference between the geophysically derived bed and the ˚kinematic" bed and need not necessarily be an error of geophysical bed determination. This first difference may play a part at stakes 11 and 24 where the actual vertical ice velocity (from stake measurements) reveals significantly higher values than the calculated one. Sharp transverse vertical shear horizons, accompanied by ˚fresh" sand and silts at the ice surface, and apparent longitudinal variations of debris geology in this zone confirm our hypothesis of a kinematic basal layer with a steeper increase than is derived from the geophysical soundings (cf. Model and assumptions). The glacier may have overthrusted its frozen margins. The calculated mass balance agrees with the measured one within ±0.9 ma^–1, ignoring again stakes 22 and 24. For these two positions the error in mass balance can clearly be attributed to the error in calculated vertical ice velocity. The differences between calculated and measured values for w_s and b can be reduced by some adaptation ofβ and ₇ which can be seen from the fact that the linear regressions of the data points (without stakes 22 and 24; Fig. 10) approximate slightly different lines than the depicted diagonal. With respect to these regressions, the measured and calculated values agree on average within ±0.5 m a"¹ for w_s (R² = 0.77) and within ±0.3 m a"¹ for –b(R²=0.91).

Mass-balance variation

In our second model step, we calculated the 1973–92 mass-balance variations for the tongue from Equation (5). To obtain a continuous series, the mass balance for years without available horizontal velocity data was modelled by introducing interpolated velocities into the kinematic boundary condition. This practice seems reasonable in respect of the smooth changes in surface velocity (cf. Fig. 11a). The mass balance for years with neither velocity nor elevation data was linearly interpolated, an uncertain procedure but one confirmed by comparison with measured mass-balance series in the Alps (cf. Haeberli and others, 1999b). Figure lib depicts the calculated time series shifted by +2.5 ma^–1 to a zero mean. For comparison, the mass-balance curve for the Griesgletscher tongue (2400–2700 m a.s.l.) as derived from stake measurements is included, shifted by +2.1 ma^–1 to a zero mean (Funk and others, 1997; Haeberli and others, 1999b). Griesgletscher, about 40 km from the Gruben area, is situated in the Swiss Central Alps and is assumed to have climate conditions roughly comparable to those at Grubengletscher. Figure 11a shows the photogrammetrically derived annual changes in elevation and the average horizontal surface speed for the tongue, both governing the temporal variability of the calculated mass balance (cf. Equation (1)). Furthermore, mean annual precipitation records and summer temperatures (July-October) are given for the station Grächen (1600 m a.s.l, about 10 km from Gruben; Fig. lie; SMA, 1995). Comparing the curves of surface speed, elevation changes and calculated mass balance clearly shows that the high frequencies of the elevation change are mainly controlled by the annual mass balance, whereas the horizontal ice velocities influence the lower frequencies. The climate records of Grächen, especially the observed variations in mean summer temperature, seem to confirm the mass-balance variations calculated for Grubengletscher tongue by a reasonable consistency. Furthermore, from 1973/74 to 1986/87 the calculated mass-balance curve for the Grubengletscher tongue and the measured one of Griesgletscher tongue show quite good agreement. After 1987, however, this agreement is strongly reduced, a fact for which there is no clear explanation. Possible reasons are a climatic difference between the two locations since 1987, or changing local glaciological conditions. The period since 1987 is one of exceptional mass losses for most alpine glaciers, not only for Gruben- and Griesgletscher. It should also be emphasized that the Griesgletscher tongue is entirely debris-free, whereas there is significant debris coverage of the Grubengletscher tongue. Therefore, a different reaction of both glaciers to periods of strongly negative mass balance could be expected to some extent, considering, for instance, albedo changes of the white ice. In summary, the calculated series of annual mass balances for the Grubengletscher tongue appears reasonable, whereas some uncertainties still remain concerning the period since 1987.

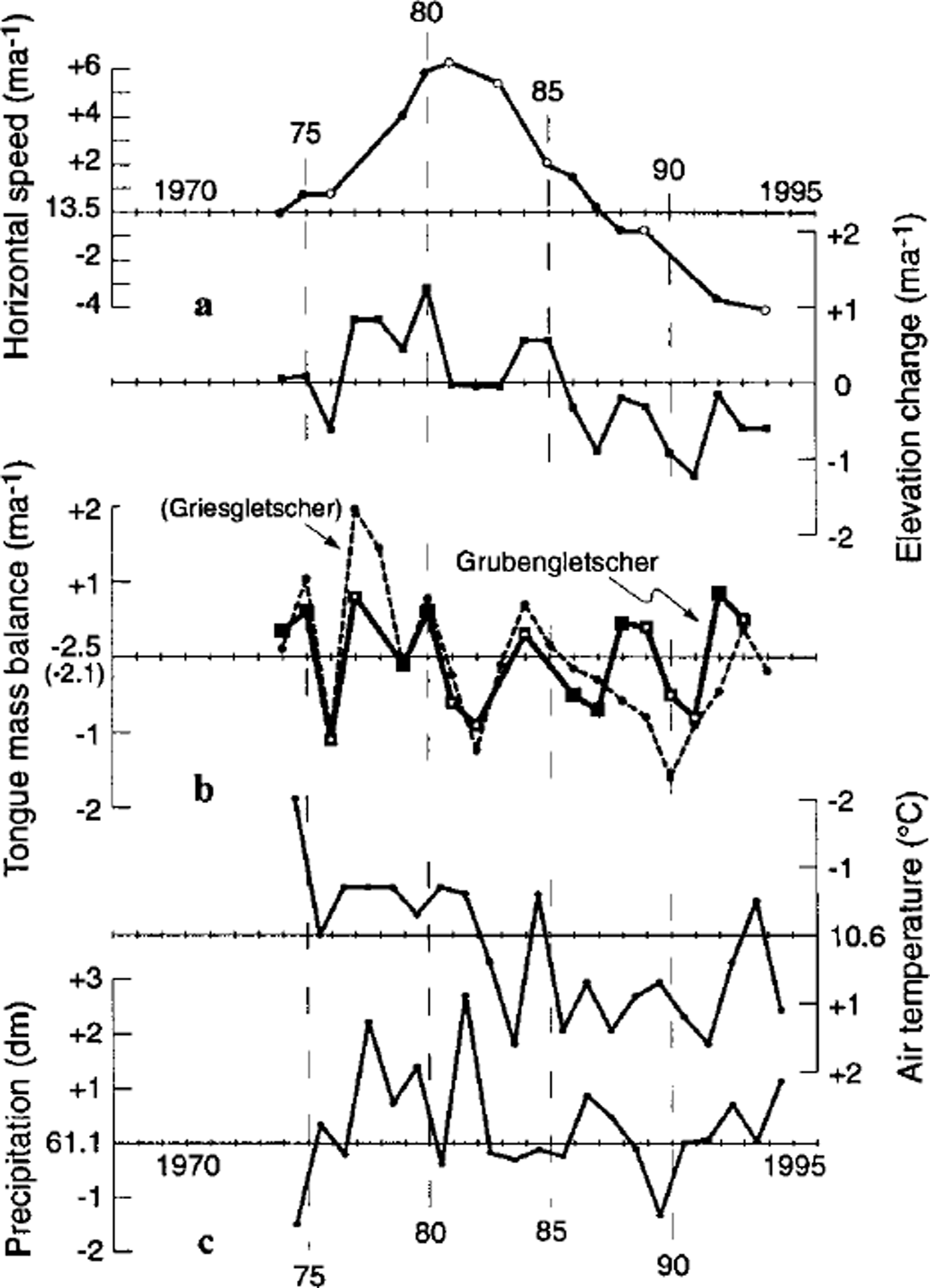
Fig. 11. (a) Average horizontal surface speed and elevation changes of the Grubengletscher tongue. Filled circles indicate photogrammetric measurements of high accuracy (annual intervals, redundant measurements); open circles mark normal accuracy (partially perennial intervals), (b) Annual mass-balance variations calculated for the Grubengletscher tongue and measured for the Gnesgletscher tongue (after Funk and others, 1997). Open squares indicate calculations from the data of normal accuracy in (a), (c) Records of mean annual precipitation and mean summer temperatures (July-October) for the meteorological station Grächen. Note the rotated algebraic sign on the vertical axis for the temperature record.

Perspectives

The kinematic boundary condition at the glacier surface, together with photogrammetrically derived elevation and velocity data, was shown to provide a valuable tool to model and analyze the spatial distribution and temporal variations of ice flow and mass balance. However, the usefulness of the presented test study on Grubengletscher is restricted by certain characteristics, for instance with respect to debris coverage, bed geometry and ice dynamics. Due to photogrammetric restrictions for snow and firn areas the presented approach is, in the present stage, primarily suitable for ablation areas (cf. Kääb and Funk, 1999). The noticeable effects of the ice-mechanical assumptions and possible errors in the basal glacier horizon are largely eliminated by modelling mass-balance variations from repeated photogrammetric measurements. Such work requires extensive photogrammetric data acquisition, but opens up a promising opportunity to remotely obtain detailed information on ice flow and mass balance, even for debris-covered ice or difficult-to-reach areas such as icefalls. If airborne radar techniques are not available, the only necessary fieldwork, which is the determination of the glacier bed geometry, can be done at any later time.

At the present stage, our approach seems especially promising for analyzing ice-flow and mass-balance distribution of specific glaciers, with a view to better process understanding. Related long-term mass-balance monitoring requires photogrammetnc series with the same temporal resolution as the desired mass balance, which will not be available for a large global number of glaciers in the near future. However, new remote-sensing technologies in the field of digital photogrammetry, airborne optical and laser scanning, air- and spaceborne synthetic-aperture radar and satellite imagery analysis will markedly improve the data availability and facilitate data acquisition in glaciology. In view of this trend, the presented approach might become a suitable tool for remote-sensing-based global glacier monitoring.