On the physical model of frozen soil

Abstract

In this paper we discuss a physical model of frozen soil based on the systems approach and reflect contemporary knowledge about the constitution, structure and properties of this complicated medium. The component composition and specific spatial cryogenic coagulant-crystalline structure as well as physical subsystems of frozen soil conditioning its physical properties are considered. Examples of the use of a model for better comprehension and explanation of some electrical and mechanical property changes of sandy-clayey frozen soils are presented and discussed. The proposed model and its hierarchy is a useful tool for planning experiments and interpreting their results.

Introduction

Cryogenic formations (types of frozen ground and ice) are complex polycrystalline, multi-component, polyphase and polydisperse physical-chemical systems which usually are in a state of unstable quasi-equilibrium. The variety of types of frozen ground accounts for a great volume of data describing their structure, texture, composition, properties and processes (Kudryavtsev and others, 1978; Popov and others, 1987; Yershov, 1997). Frozen-ground properties, especially mechanical and electrical, are noticeably influenced and often controlled by liquid-solid interfaces, i.e. inter-grain boundary zones which include both liquid-phase and solid admixtures, as well as by constitutional ice. It is essential, however, to have an adequate physical model of frozen ground based on currently available information, in order to understand fundamental and specific features of these grounds, which are widely distributed (extending over about 50% of the Earth’s land surface). The development of a model elucidating the formation, and the changes in physical and other properties, of (both seasonally and perennially) frozen soils would be of great practical significance for the solution of many scientific and engineering problems. The systems approach seems the most appropriate for developing such a model, with the frozen soil being considered as a complex macrosystem.

The following assumptions are made: the system is a multitude of correlated elements forming a certain structure which ensures the integrity of the system and its particular response (behaviour) to environmental impact, including force influences. Integrity is one of the principal properties of a system. One of its manifestations is that properties of a system as a whole are not an additive sum of its constituents but depend on interrelations between the components. In general, any real heterogeneous system lies between two extremes: absolute additivity and absolute integrity (Ostreikovsky, 1997).

It is extremely difficult to formalize a description of frozen ground, which is a very complicated, heterogeneous, polyphase and often heteroporous formation. Current analytical models of granular and capillary-porous media, additive mixtures, etc., are inadequate for cryogenic media. Given the present state of knowledge, a mathematical model of such a system would be a considerable simplification. To improve understanding of its physical nature, it would help to begin with a linguistic (conceptual, verbal) physical model of frozen soil based on the systems approach. Such a model is proposed and described, as well as some examples of its use in explaning experimental data on the electrical and mechanical properties of sandy-clayey frozen soils.

Frozen Soil as a Complex Macrosystem

Frozen soil is a complex macrosystem distinguished by the coexistence of ice and unfrozen water, as well as by a specific cryogenic spatial structure which accounts for its regular functioning under certain environments and external force effects. Within certain limits, it is an adaptive, self-restoring (relaxing) system which may be represented by hierarchies with relatively weak bonds (Ostreikovsky, 1997). As the basis for a model of frozen soil, we suggest two correlative hierarchy types as follows:

In the context of the object’s constitution:

1. A. Component composition of the frozen soil and volume relationship between its components.

2. B. Spatial cryogenic coagulant-crystalline structure (SCCS), which appears and develops in the process of freezing and constitutional ice formation.

In the context of the macrosystem’s response to external actions:

1. C. Physical subsystems.

2. D. Mechanisms of the responses and corresponding physical properties.

Each of these aspects is discussed briefly below with a view to its importance for understanding of frozen-ground properties and regularities in their changes.

Component composition

The component composition of frozen soil consists of: a mineral solid part (silicate grains and grain aggregates), pore and segregated ice (usually impure), unfrozen ˚water" (actually, pore solution) and a gaseous phase. To describe this one may assume that V_m + Vi, + Vn + V_g = 1, where V_m,Vi,Vu and V_g are volumes of mineral solid part, ice, unfrozen water and gas, respectively, in a unit of soil volume. It should be noted that the unit chosen must be big enough to ensure representativeness of the characteristics, with due consideration for the given cryogenic structure and texture. Changes in the component composition of frozen soil of some initial porosity, when the total volume, W_v, increases may proceed in two ways depending on the following conditions:

1. (a) under V_m = const. ≠ 0, partial initial saturation, constant porosity, Vi increases, hence V_g decreases;

2. (b) under V_g = 0, complete initial saturation, Vi, increases, hence V_m decreases.

In the first case, the frozen soil is considered to be a four-component system where, as W_v grows until it reaches the porosity volume of the system, the ice-cement content in pores also increases. In the second case, initially there exists essentially a three-component system where V_m and Vu are reduced as W_v and therefore Vi, increase; the system is in its ultimate state corresponding to polycrystalline ice.

All the components mentioned are highly diversified and are briefly discussed below.

Mineral solid part

The mineral solid part of frozen sandy-clayey soils consists of both primary silicate minerals (resulting from physical weathering of rocks such as quartz, feldspars and micas) and secondary ones, phyllosilicates (montmorillonite, illite, kaolinite), which are products of chemical weathering and diagenesis. The latter are distinguished by a greater specific surface of complicated non-uniform morphology and enhanced capacity for sorption, ion exchange, swelling, etc. The soil may also contain poorly soluble salts, clathrates, organic and organic-mineral substances (e.g. peat, humus, oxalates, acetates). Humus matter is of considerable importance in the formation of clayey aggregates. Characteristics of the mineral solid part are polydispersity and heteroporosity; these properties, together with the influence of cation exchange, should be taken into account when considering the liquid-phase formation, especially in clayey frozen soil.

Constitutional ice

Constitutional ice in frozen soil is highly diversified in size, configuration, texture, impurities and structure of polycrystalline aggregates. There are two kinds of constitutional ice: ice-cement formed near mineral particles (including many varieties, from contact ice to basal ice (Kudryavtsev and others, 1978; Zhestkova and others, 1980)) and segregated ice. Their spatial distribution controls the cryotexture of frozen soil. During freezing of clayey water-saturated soil, ˚ice-rich" clusters commonly occur; these are ice formations which include non-aggregated clay particles and are similar in size to clayey aggregates and pure-ice inclusions. However, even so-called ˚pure" monomineral ice is actually heterogeneous matter containing a liquid phase and impurities in the inter-grain boundary zones of crystallites and between crystallites. Finally, microstructures of frozen soil are found to be unstable, even for slightly changing temperature (Zhestkova and others, 1980).

Liquid phase

The liquid phase of frozen ground differs noticeably from common free water, though the term ˚unfrozen water" is still widely used. The differences may be summarized as follows:

1. (1) liquid matter in the soil is always a solution; saline sandy-clayey frozen soils differ from non-saline ones only in a definite initial critical (limit) concentration of the pore solution which depends on its ionic composition and the mineral matrix type (Frolov, 1996,1998);

2. (2) unfrozen pore solution resides near (or between) different surfaces of solid grains, such as ice-mineral-particle, ice-ice and ice-gas (quasi-liquid layer); the grain surfaces are irregular even in the case of uniform mineral composition;

3. (3) as a result, the liquid phase in frozen ground is always inhomogeneous, i.e. it is marked by allotropy and in essence presents discrete (semi-discrete) domains of different liquid phases with a structure of hydrogen bonds that varies in internal energy and entropy, and therefore in eutectic and other parameters of the solution within the soil;

4. (4) these phases are in equilibrium with impure ice for temperatures below 0°C, and cannot be considered as metastable states due to the external influence of grain surfaces; that is to say, they have a somewhat reduced (when compared to free water) chemical potential;

5. (5) the presence of impure ice noticeably modifies the energetic state of liquid phase in discrete domains, as well as the electrochemical activity of the medium, and thus changes the electric polarizability and dielectric permittivity of frozen soil with respect to a thawed soil.

The above allows better understanding of liquid-phase freezing over an extended interval of negative temperatures.

Gaseous phase

Gaseous-phase composition affects the properties of frozen soils only in the case of pores not completely filled with ice and liquid phase. It should be noted that besides air and water vapour, there are gaseous hydrogen compounds (CH₄, H₂S, P₂H₄, etc.) in noticeable quantities in soils enriched with organic matter.

However, even detailed knowledge of the component composition would not enable reliable estimates of the frozen-soil physical properties to be obtained, because of interaction between the components and resulting violation of the additivity principle.

Sccs

In conformity with physical-chemical mechanics (e.g. Rebin-der, 1979; Shchukin, 1992), heterogeneous, dispersive, liquid-containing media form stable spatial structures by way of two types of contacts: coagulation (through liquid interlayer) and phase or crystallization-condensation (due to sintering or mutual coalescence of solid phases). There may exist combined contacts varying both in configuration and size of contacting areas and in thickness and composition of liquid and quasi-liquid interlayers. Cohesion forces at coagulant contacts are about l0^–7 to l0–N, when the sizes of soil particles are l-10μm, and those at phase contacts are ∼KT³ N or more, depending on the values in the contact area and its physical-chemical features.

This approach, as applied to various types of frozen ground and ice, led us to conclude that the SCCS appears during their formation and offers the key distinguishing feature of these new geological objects (Frolov, 1998). The principal constituents of the SCCS are: (a) ice grains (crystals and crystallites) ― ice matrix; (b) mineral solid part grains ― mineral matrix; (c) inter-grain zones including unfrozen liquid phase, gases, impurities and defective boundary layers of solid phases ― matrix of defects. The latter is the most variable and informative element of SCCS state and exerts primary control over the most sensitive, electrical and mechanical, characteristics of the frozen ground as macrosystem.

The presence of liquid phase accumulated within inter-grain zones accounts for their plasticity, and they often act as traps for expanding microfissures, which in turn influences the frozen-soil strength (especially the tensile strength). The inter-grain zones in frozen soil are undoubtedly non-uniform. Electrically uncompensated ˚active centres" are arranged in strips or spots on grain surfaces, which accounts for insular (discrete) adsorption of molecules or ions from liquid or vapour. The discrete distribution is traced as distorted structure in adsorbed phases over considerable distances (up to 10³ nm) from the adsorbent surface. The concept of homogeneous films of adsorbed water (persisting since I. Langmuir’s time) is highly simplified.

All three matrices of the SCCS are integral elements of a new (cryogenic) macrosystem. This is also true of the mineral matrix which might seem, at first glance, to be a ˚passive" element inherited from the initial medium, i.e. thawed soil.

Spatial pattern, quantitative relationships and correlations between the three SCCS matrices depend on initial conditions of the soil freezing, as well as on its further evolution in changing environments. Four stages of SCCS formation and development may be recognized, from the appearance of the odd individual ice crystal to practically complete freezing of the liquid phase (Frolov, 1976, 1998); each stage is characterized by specific features of cryogenesis and the properties of the macrosystem, while taken as a whole they allow us to produce a unified concept of the physical-chemical basis of the laws and mechanisms of frozen-soil physical-property formation and variability.

The specific character of inter-grain zones and impure constitutional ice produces a noticeable effect on structural cohesive forces which in turn control frozen-soil strength and deformability. Bonds within the ice and clay aggregates as well as between the grains of the medium vary considerably in strength, which results in their serial breakage (beginning with the weaker ones) in the mechanical stress field. Such a mechanism can produce a partial relaxation of stress, and consequently damping (stabilization) of the micro-cracking process, that under certain conditions accounts for the presence of the tensile-strength maxima. The macro-rupture of a medium will begin when an average load per single bond is equal to an average strength value for still unbroken bonds.

Physical subsystems and properties

In studies of electrical and mechanical properties of frozen ground as a complex macrosystem, a common practice is to choose a certain kind of physical field acting upon the object and to vary its intensity, duration and regime of application, frequency range, polarization, etc., as well as the frozen-ground temperature. In the process, ˚physical filtration" of a kind is performed, and the registered result reflects processes taking place primarily within a subsystem of the complex macrosystem. Part of the information is inevitably lost (as in any data processing), but the other part yields much finer details. It is reasonable to designate as a separate physical subsystem those degrees of freedom of internal movements (i.e. physical-chemical transformations) which are characteristic of processes controlling the specific properties under consideration. Therefore, a complex macrosystem, frozen soil, should be considered as an assemblage of physical subsystems combined into SCCS and related to its principal elements (Fig. 1). It is essential that a subsystem after excitation should evolve towards quasi-equilibrium (relaxation) at a greater rate than the macrosystem as a whole. In that case, external action on the macrosystem using a certain physical field may result in selective excitation of individual subsystems; that opens up new possibilities in the investigations of their relaxation regularities, hence the peculiarities of corresponding physical properties. In the context of the matter’s structure and response to various physical fields, action on a complex macrosystem, a number of physical (nuclear, electronic and ionic) subsystems may be distinguished (Fig. 1), each of which may include several varieties. For example, an electron-hole subsystem that is ˚bound" would characterize dipole moment formation and variations within atoms or molecules; one that is ˚quasi-free" would control transfer phenomena (electrical and heat conduction). An ionic subsystem also may be "bound"or ˚quasi-free", i.e. under external field action the ions would oscillate or move progressively over a considerable distance. Also possible are ˚semi-bound" ion and electron subsystems where electrically charged particles may move in translatory mode, though only within a confined space which results in temporary surplus charge accumulation (sorption) and formation of polarized discrete portions of the medium (domains). Bound ionic and electron dipole subsystems (ion associates and molecules of ice and water, crystallohydrates of salts, etc.), electron-hole subsystems (aluminosilicate grains) and nuclear spin subsystems would also be relevant. In particular, the excitation and study of the response of the nuclear spin subsystem of H ₂ 0 opened the way for the study of frozen-soil-phase composition using the nuclear magnetic resonance spectroscopy technique.

Fig. 1. Hierarchy of frozen soil as a complex macrosystem.

When comparing the different properties of a complex medium, it is important that they should have a common causal factor, i.e. their variations should be controlled by the response of the same subsystems or subsystems reflecting similar changes in the medium (e.g. changes of the phase composition in frozen soils). Only for this condition is it possible to establish reliable correlations between different properties; otherwise the correlations are either purely formal, or applicable only in particular cases. Studies of relaxation processes in heterogeneous media under intended action aimed at excitation of separate subsystems are therefore exceedingly important; sometimes they offer the only way of recognizing the kinetics of complex physical-chemical transformations and obtaining information on the role of individual mechanisms and their interrelations.

Examples of Model Use

The model opens the way for better understanding and interpretation of available experimental data on the electrical and mechanical properties of frozen soils. Limited space allows us to give only a few examples. As mentioned above, an indicator of the integrity of frozen ground as a macrosystem is that its properties are inconsistent with the additivity principle which takes into account only the content by volume of the components and their corresponding properties. It is especially apparent in frozen soils with respect to the relative dielectric permittivity s>. Thus, according to experimental data (e.g. Frolov, 1976, 1998; Gurov, 1983), at frequencies of 10² to 105Hz, with the total moisture content varying from 1–2% to 40% and temperatures up to –60°C (for clays), the ε′ value of frozen non-saline sandy-clayey grounds may be as high as a few hundreds or even thousands (Olhoeft, 1977; Maeno and others, 1992). But values of ε′ for water and ice do not exceed 102, and for silicates they range from 4 to 10. It should also be noted that the ε′ value of ice decreases with reduction in temperature. Hence, equations for additive mixtures cannot explain the experimental results in which the ε′ value of the mixture exceeds those of its constituents. Nevertheless these abnormally high values of ε′ obtained for frozen soils and their frequency dependence (Figs 2) could be explained using our model based on the important notions of heterogeneous state and discrete domains of unfrozen liquid phase within inter-grain zones. An application of external electromagnetic field results in migration of ions in the domains, accumulation of divided charge and rise of electric macrcdipoles, with the values of electrical moments depending essentially on the mobility and concentration of ions as well as on the duration of the action of the electromagnetic field, and hence its period (or frequency). That such a mechanism operates is confirmed by the fact that it allows us to explain satisfactorily the non-linear electroacoustic effect in frozen soil observed at doubled frequency compared to that of the applied electric field (Frolov, 1998). With increase of electromagnetic field frequency, or decrease of the frozen-soil temperature, the contribution of the macrodipole polarization mechanism is considerably reduced (Fig. 2), and obtained values of ε′ approximate those calculated using additive mixture formulae. In the first case, this is due to decrease of the time of ion migration and charge division within liquid-phase domains; in the second case, it is due to decrease in domain size because of the liquid phase freezing out and usually lessening the mobility of ions within it. Thus, at high frequencies of 10 to 103MHz, ∊ ’― 4 was obtained (Delaney and Arcone, 1982) for frozen eolian sand, and this value does not depend on total moisture content (which was varied over two-fold), nor on temperature. This correlates well with Figure 2b and means no macrodipole effect has been displayed. However, according to the work mentioned above, the temperature dependence is quite clear in frozen loess: the e’ value decreases from 13–12 at –2°C to 7–6 at –18.8° and –21.8°C, and only the final values approximately correspond to equations for statistical mixtures. At higher temperatures there is a noticeable contribution from the macrodipole mechanism of polarization. We believe that its presence at such high frequencies is due to considerable unfrozen liquid-phase volumetric content ( ∼ 5 ― 6% up to –15°C, indicating some salinity of the soil) in many of the small-size domains in inter-grain zones of loess particles (the latter are usually aggregates of clayey and calcium carbonate components), as well as to high mobility of ions within domains.

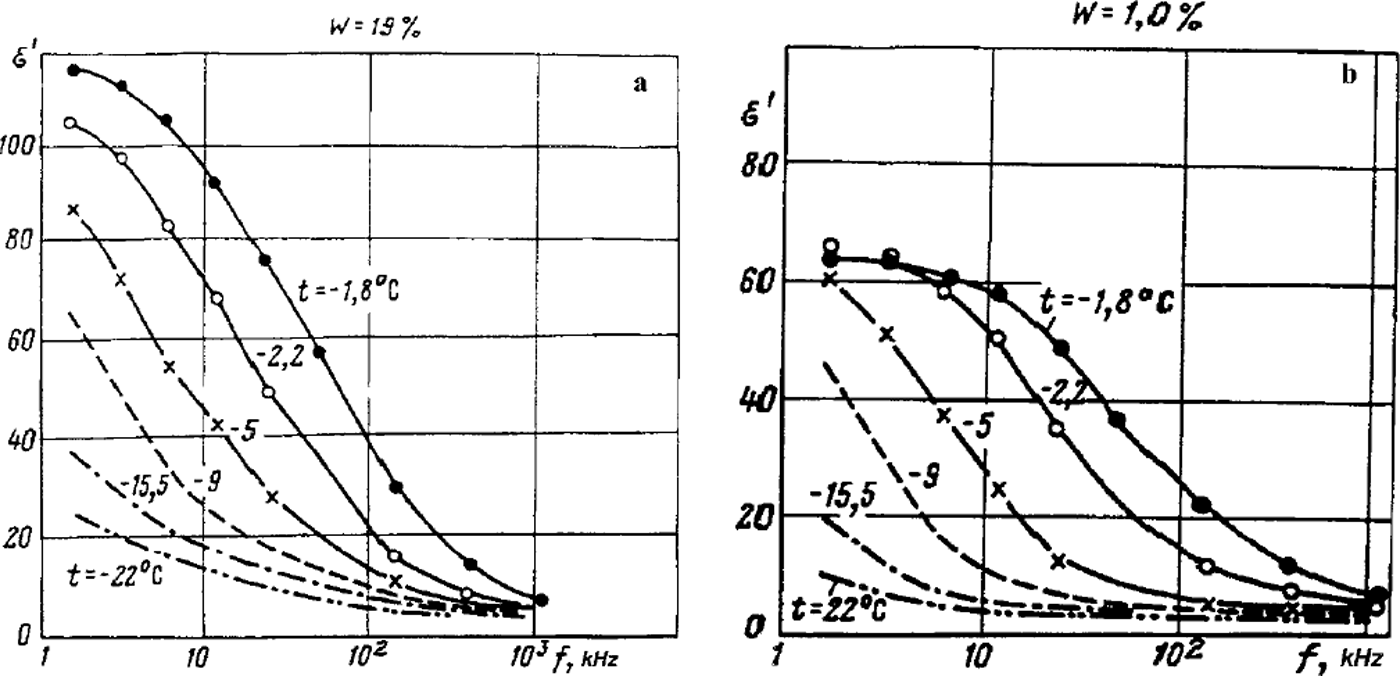
Fig. 2. Dispersion of dielectric permittivity at middle frequencies for frozen sand with different total mass wetness ( W) and for various temperatures, (a) W = 19%; (b) W=l%.

Another indication of the dominant role of inter-grain zones is the existence of boundary temperatures, at which the dynamic elastic moduli (obtained by use of an ultrasonic technique) of the initially water-saturated frozen soil were found to be independent of the volume ice content over a wide range of values (Frolov, 1976). Figure 3a shows the module values obtained for the Glukhovetsky kaolin at those temperatures: for the shear modulus –μ at t ≈–12°C, Young’s modulus E at t ≈ –9°C, and the bulk modulus K at t ≈ –5°C; the module values correspond to those of polycrystalline ice for indicated temperatures beginning from soil–ice content by volume about 35% up to about 90% (basal cryotextures). At temperatures above the boundary values, the inter-grain zones of frozen kaolin are less elastic (because of the corresponding liquid-phase content) than those of polycrystalline ice, so an increase in ice-volume content in the soil results in growth of elastic moduli of the medium due to decrease in the proportion of the mineral solid part (consequently of liquid phase) and coagulation (weak) contacts between the solid matrix grains. At temperatures below the boundary values, the rigidity of inter-grain zones in the frozen kaolin with massive cryotexture as a whole exceeds that of polycrystalline ice; therefore elastic moduli would decrease with increase in the soil of the ice proportion by volume. Similar results were obtained by Vinson and others (1983) during studies of the Young’s modulus (using the resonance vibration technique) of natural samples of frozen loess from the Fairbanks region, Alaska, differing in total mass wetness. The boundary temperature of this frozen soil was about –2.5°C at E «8GPa (Fig. 3b), which closely corresponds to that of polycrystalline ice at the same temperature. In both figures the boundary temperatures correspond to the unfrozen liquid-phase bulk proportion ― 5–6%. The boundary temperatures under discussion must depend on the composition and dispersiveness of the SCCS mineral matrix, since the matrix also controls the formation and mechanical properties of the inter-grain zones and those of the frozen soil as a whole.

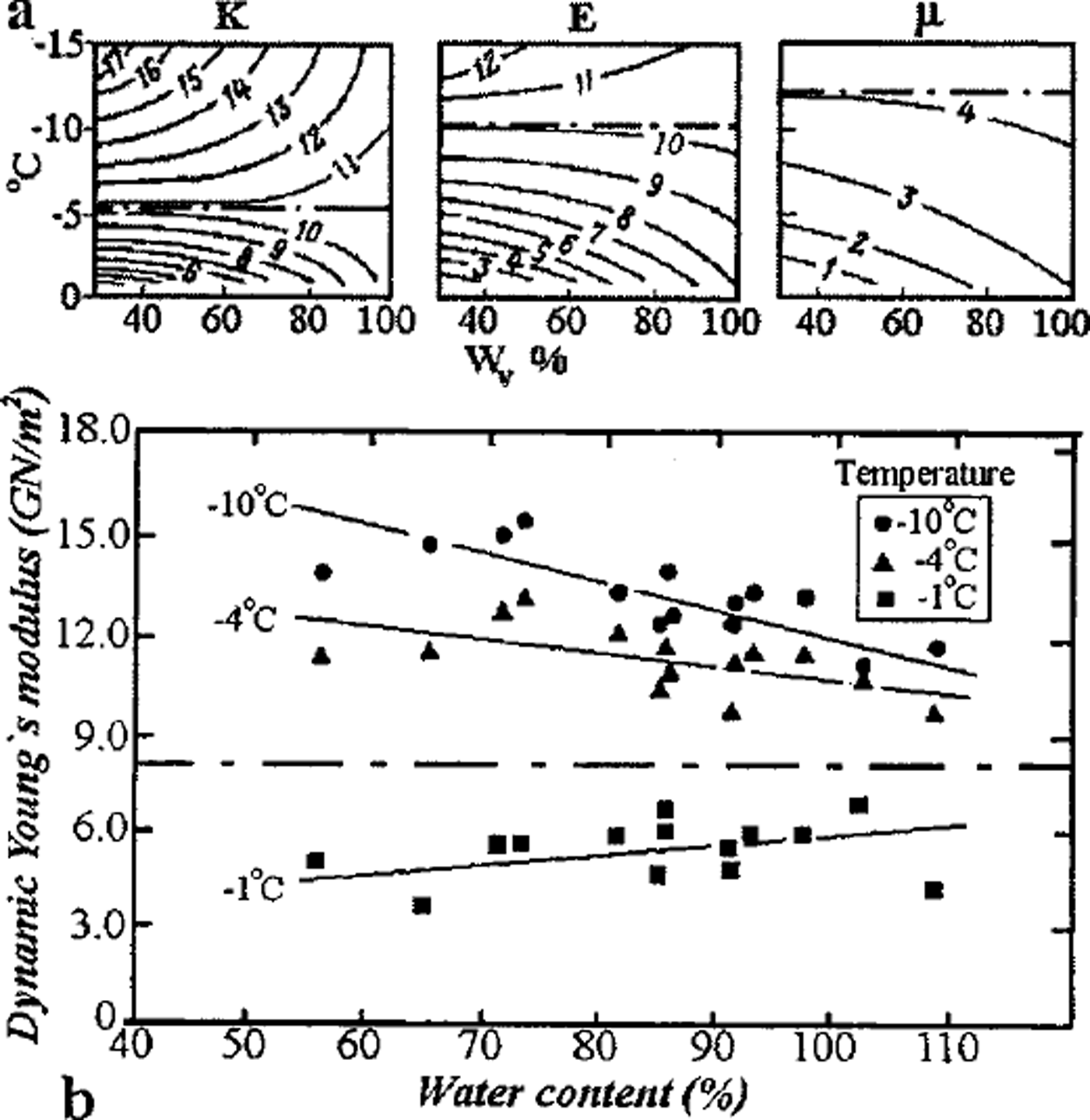
Fig. 3. Boundary temperatures for elastic Young’s moduli of frozen soils in saturation by ice: (a) kaolin, (b) loess.

Our model also demonstrates the established empirical relationship (Frolov, 1976, 1998) between dynamic Young’s modulus of saturated frozen sandy-clayey soils with massive cryotexture and the degree of their mineral matrix dispersiveness: E(t) = k(t) log d + E’(t), where d is soil particle size (in _μm), E’ is the modulus value in GPa for heavy clay ( d ≈ 1_μm) and the parameter k(t) increases from 9 to 11.5 GPa with a temperature increase from –40° to –2°C In the same temperature range the E’ value changes from 14 to 3 GPa. During the process of freezing of non-saline soils of various mineral matrices from frozen clays to sands, the increasingly rigid inter-grain zones formed are marked by decreased content and the increasingly homogeneous state of the liquid phase; this accounts for the noticeable growth of the moduli of elasticity.

The composition and state of inter-grain zones and the ice matrix have a pronounced influence on the frozen-soil strength, on their thermal deformations and on the creep. Concerning strength, from our model it is clear that there must be a reasonably close correlation between parameters of strength and elasticity. This has been shown by Frolov (1998) for a compressive strength and longitudinal elastic-wave velocity. For sandy-clayey soils with massive cryotexture, this correlation was proved linear (in semi-loganthmic scale) with the parameter, the temperature of frozen soil. In line with our prediction, the tensile strength is more sensitive to changes in the state of the inter-grain zones which determine the transition from quasi-plastic to brittle mode of the medium failure. Therefore, the peaks of tensile strength should occur as the frozen-soil temperature falls. Such maxima were confirmed in direct laboratory experiments by E. Shusherina and others with samples of frozen soil and underground ice (see Frolov, 1998).

Finally, in saline frozen soils the inter-grain zones are of still greater importance for electrical and mechanical properties of the media, and at a certain initial concentration C; of the pore solution they may even suppress or attenuate the influence of the mineral matrix (Fig. 4). As Figure 4a shows, the electrical resistivity of frozen soil at C_i ≥ 5 g IT¹ is independent of the mineral matrix composition from sand to kaolin and is controlled only by initial pore-solution concentration and soil temperature. A second example in this context is shown in Figure 4b, where at Cⁱ ≥ 12 g IT¹ the dependence of Young’s modulus on the soil plasticity index becomes inverse. These features are due to a higher proportion of unfrozen pore solution of high concentration within inter-grain zones and to the resulting decrease in rigidity of the zones, notably in saline frozen sands.

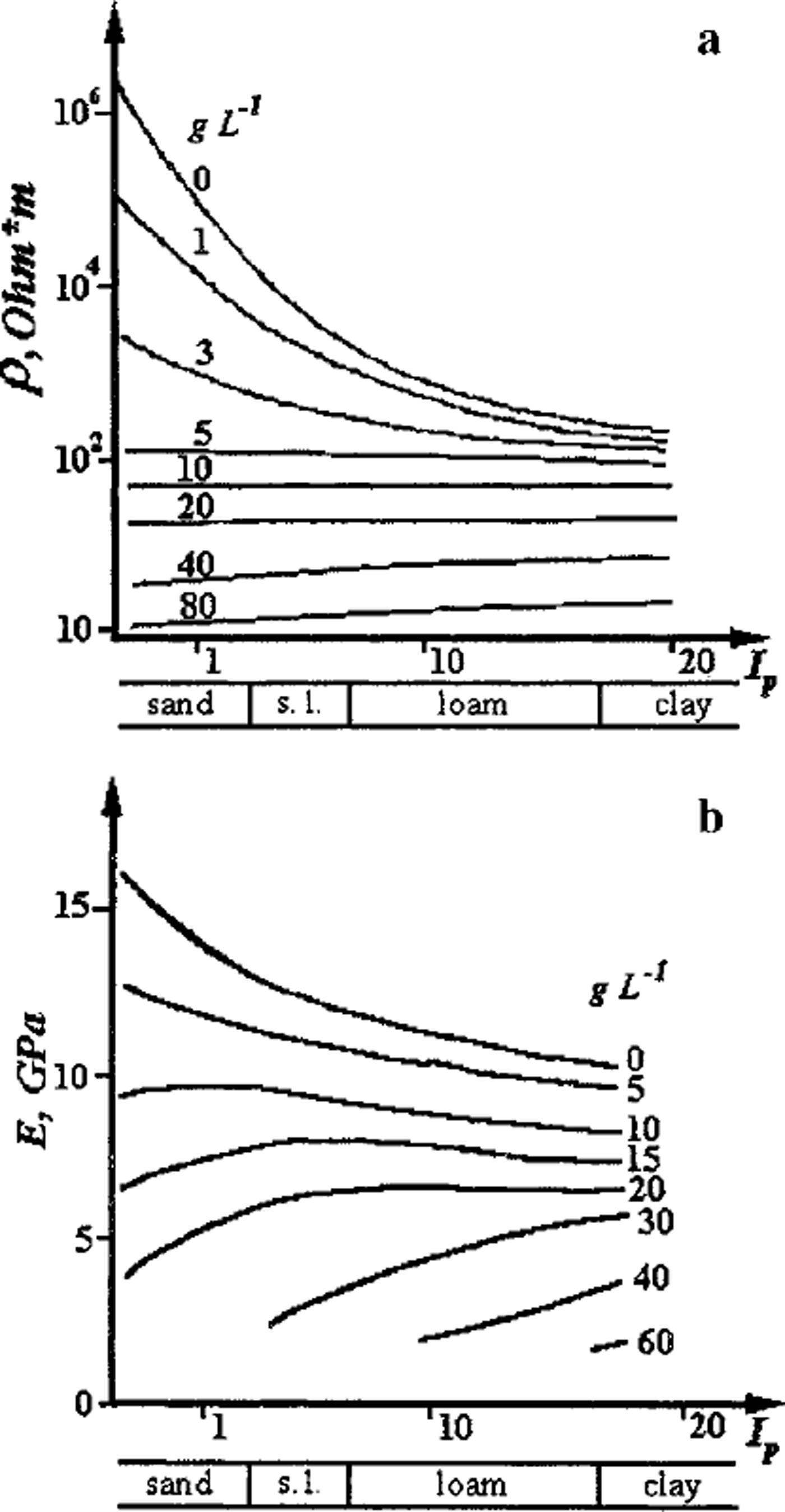
Fig. 4. Influence of inter-grain zones, with increasing initial concentration of pore solution in g L–1¹ (curve index), on (a) electrical resistivity and (b) Young’s modulus of frozen sandy –clayey saline soils (I_p is plasticity number). Temperature ― 5°C.

Concluding Remarks

The data discussed above show that the physical model considered describes frozen-soil behaviour quite adequately. The model provides a consistent explanation and better understanding of the specific features and experimentally established laws of the changes in mechanical and electrical properties of frozen soils in the processes of freezing and thawing. We infer that joint studies and analysis of the processes of mechanical and electrical relaxation are desirable and that it should be possible to find reliable correlations between mechanical and electrical characteristics of frozen soils. Such correlations would provide the basis for developing non-destructive acoustic and electromagnetic (including remote-sensing) methods with which to estimate and control the strength and deformation characteristics of frozen soil in situ. It should be possible to develop ways of influencing the soil SCCS through its physical subsystems in order to create some fixed needful properties of frozen soil, or to predetermine the regime for changing them under certain conditions.