Initial field observations on Qaanaaq ice cap, northwestern Greenland

Abstract

To study the glaciological processes controlling the mass budget of Greenland’s peripheral glaciers and ice caps, field measurements were carried out on Qaanaaq ice cap, a 20 km long ice cap in northwestern Greenland. In the summer of 2012, we measured surface melt rate, ice flow velocity and ice thickness along a survey route spanning the ice margin (200m a.s.l.) to the ice-cap summit (1110m a.s.l.). Melt rates in the ablation area were clearly influenced by dark materials covering the ice surface, where degree-day factors varied from 5.44 mm w.e. K^–1 d^–1 on a clean surface to 8.26 mm w.e. K^–1 d^–1 in the dark regions. Ice velocity showed diurnal variations, indicating the presence of surface-meltwater induced basal sliding. Mean ice thickness along the survey route was 120 m, with a maximum thickness of 165 m. Ice velocity and temperature fields were computed using a thermomechanically coupled numerical glacier model. Modelled ice temperature, obtained by imposing estimated annual mean air temperature as the surface boundary condition, was substantially lower than implied by the observed ice velocity. This result suggests that the ice dynamics and thermodynamics of the ice cap are significantly influenced by heat transfer from meltwater and changing ice geometry.

1. Introduction

Coastal regions of Greenland contain a number of glaciers and ice caps (GICs), which are physically separated from the Greenland ice sheet. The total area of these ice bodies (~1.3 × 10⁵ km²) accounts for 7% of the entire ice cover over Greenland (Rastner and others, 2012), so their volume change has substantial influence on sea-level rise. Because the GICs are located at relatively lower elevations, they are susceptible to the recent strong warming trend in Greenland (e.g. Hanna and others, 2012). Recent estimates of total ice mass loss of Greenland’s GICs are 28–41 Gta–¹, depending on the definition of the GICs in terms of the degree of connection with the ice sheet (Bolch and others, 2013).

Despite the importance and the large mass loss revealed by satellite remote-sensing techniques, only a few field observations have been reported from Greenland’s GICs. One of the most detailed field datasets is available for Mittivakkat Gletscher, southeast Greenland. The mass-balance record of this glacier shows increasing mass loss since 1995 (Mernild and others, 2011), and the mass loss in 2009/10 was more than twice the mean over the previous 15 years. Importantly, recent changes in the GICs are not uniformly distributed over Greenland. In northeast Greenland, the surface elevation change over the Flade Isblink ice cap from 2002 to 2009 was near zero (Rinne and others, 2011), suggesting spatial variability in the mass-balance trend. Thus, observational data from different regions are needed to better understand the drivers of the changing mass balance of the GICs as well as the mass-balance variations over Greenland.

A likely reason for the recent mass loss of the GICs is rising air temperature, but other processes (e.g. surface albedo and ice velocity) may be playing a crucial role in the changing mass balance. Reduction in the ice and snow surface albedo is one such potentially important process. Over the ablation zone of the western Greenland ice sheet, a large area of the ice surface is progressively darkening, and the area of the dark region is expanding (e.g. Wientjes and Oerlemans, 2010). Similar changes in the ice surface appearance are also expected on peripheral GICs. It is believed that melt increases in the dark regions because of low albedo, resulting in more negative mass balance of the ice sheet and the GICs. The effect of a darkening ice surface on the mass balance has been studied and confirmed in other regions (e.g. Oerlemans and others, 2009), but few in situ data exist in Greenland. Another important process is the influence of meltwater on the ice dynamics. The magnitude of surface melt and its temporal variability have the potential to control the flow velocity of the predominantly cold ice sheet (Zwally and others, 2002; Schoof, 2010; Colgan and others, 2012), which indirectly affects the mass budget by changing the rate of ice transport to lower elevations. Seasonal flow velocity changes are reported in the Flade Isblink ice cap (Palmer and others, 2010), but field data on short-term velocity variations are lacking in Greenland’s GICs.

In this paper, we report melt rates, ice velocity and ice thickness of Qaanaaq ice cap (QIC) as the results of the initial glaciological investigation on this ice cap in northwestern Greenland. We also present preliminary results of numerical experiments performed with a glacier flow model based on the ice thickness data.

2. Field Measurements

2.1. Qaanaaq ice cap

Qaanaaq ice cap (77828’ N, 69814’W) is located in northwestern Greenland, covering an area of 289 km² and an elevation range of 30-1110m a.s.l. over the central part of a peninsula (Fig. 1). The peninsula is populated by about 600 people in the village of Qaanaaq located on the southern coast. Climatic data since 1996 are available from regional weather stations, but no glaciological observations have been reported on the ice cap. A number of outlet glaciers protrude from the ice cap for distances of 1-10 km. Our study site in the 2012 summer field campaign was Qaanaaq Gletscher, which flows southwest from the southern part of the ice cap (Fig. 1c). We performed field observations along a survey route, which follows a glacier flowline from one of the highest peaks of the ice cap to the terminus of Qaanaaq Gletscher.

Fig. 1. (a) Satellite image (Landsat, 5 February 1999) showing northwestern Greenland including Qaanaaq. The inset shows the location of the region in Greenland, and the box indicates the area shown in (b). (b) Satellite image of QIC (ALOS PRISM, 25 August 2009). The locations of Qaanaaq Airport and the temperature measurement site on the ice cap (SIGMA-B) are indicated by asterisks. The box indicates the area covered by (c). (c) Satellite image (ALOS PRISM, 25 August 2009) of the study site, showing the locations of the measurement sites for surface melt (+), ice velocity (*), ice radar (*) and the GPS reference station (*). The arrows are horizontal surface flow vectors from 18 to 29 July 2012.

2.2. Melt rate

We installed seven 2 m long aluminum poles along the survey route to measure ice/snow melt rates (Fig. 1c). The installation sites ranged from 243 to 1079ma.s.l. (Table 1). When the poles were installed on 18 and 20 July 2012, ice was exposed at the lower five sites (Q1201-Q1205), whereas the upper two sites (Q1206 and Q1207) were covered by a snow layer. The snow cover was wet and classified as granular snow (Fierz and others, 2009). The poles were drilled into the surface using a mechanical ice drill (Kovacs) equipped with an electric drill driver (Makita HR262DRDX). The distance from the top of the pole to the ice/snow surface was measured with an accuracy of 5 mm. We repeated the measurements with intervals of 1-9 days from the dates of the installation until 29 July. Water equivalent melt rates were computed assuming ice densities of = 910kgm-³ at Q1201-Q1205, and firn densities of ρ = 500kgm^–3 at Q1206 and Q1207. Because firn density was not measured on site, it was estimated from within a range suggested for granular snow (Paterson, 1994), and its uncertainty is about ±20%.

2.3. Ice velocity

The poles were also used for ice velocity measurements. The three-dimensional (3-D) coordinates of the poles were surveyed twice, on the date of installation and on 29 July. We mounted the antenna of a dual-frequency GPS receiver (GNSS Technologies Inc., GEM-1) on the top of the poles to record GPS satellite signals every 1 s for at least 30 min. These GPS data were post-processed in static mode with those collected by a reference GPS station established within the village of Qaanaaq (Fig. 1c). The same device and recording intervals were used for the reference station. The coordinates were computed with the GPS processing software RTKLIB (http://www.rtklib.com/rtklib.htm). According to the estimate of the software, the standard deviations of the GPS positioning are generally <5 mm in the horizontal direction and <20mm in the vertical direction. Vertical velocity was not obtained at Q1207 because the GPS solution was not accurate enough due to poor satellite configuration.

The survey pole at Q1203 was equipped with a permanent GPS station from 18 to 26 July. The satellite signals were recorded continuously with the same type of GPS receiver powered by a battery (13 Ah) and a solar panel

(20 W). The GPS data were split into 30min segments to compute 3-D displacements. Each of the 30 min data segments was processed in a static mode with data recorded at the reference station as described above. Ice velocity was computed after filtering the half-hourly positioning data using a Gaussian smoothing routine with a time window of 3 hours.

2.4. Ice thickness and bed elevation

Ice thickness was measured approximately every 200 m along the survey route (Fig. 1c). We used an ice-penetrating radar system manufactured by The Ohio State University, USA, which consists of a transmitter, receiver and 20 m long dipole antennas. The central wave frequency was 5 MHz. Vertical resolution expected for ice thickness measurements with this frequency is 8.4 m. The transmitter and receiver were placed 20 m apart along the survey route, and the antenna cables were stretched perpendicular to the route. To compute ice thickness from two-way travel time of bedreflected radar signals, wave propagation speed through the glacier was assumed to be 168m ms^-1. We took this value that has been proposed for the speed in solid ice (Glen and Paren, 1975), because a surface firn layer was observed only in the uppermost regions (>970ma.s.l.). Glacier thickness may have been slightly underestimated in the firn-covered region because of this assumption.

Ice-cap surface elevation was surveyed by a kinematic GPS positioning technique at the sites of the radar sounding. We used a dual-frequency GPS receiver (Leica System 1200) as a rover station and post-processed the data with those from the aforementioned reference station. The ice thickness measured by the radar sounding was then subtracted from the surface elevation to obtain ice-cap bed elevation.

2.5. Air temperature data

Air temperature recorded by a weather station at Qaanaaq Airport (77°28′N, 69°14′W; z=16ma.s.l.) located at 3.5 km northwest of Qaanaaq (Fig. 1b) was used in this study. Daily mean, minimum and maximum temperatures at this station since 1996 are distributed by the US National Oceanic and Atmospheric Administration. Daily mean temperature from 2010 to 2013 was used to study temperature conditions and estimate surface melt.

We also measured air temperature on the ice cap at ~1 km to the east of the survey route (778310 N, 698040W; z=944ma.s.l.) (SIGMA-B in Fig. 1b). Hourly temperature measurement has been in operation since July 2012 using a sensor (Vaisala, HMP155) installed at 3.0m above the surface. This record was used to compute the temperature lapse rate over the ice cap.

3. Results of Field Measurements

3.1. Melt rate

Melt rates measured at Q1201-Q1207 ranged from 7 mm w.e.d^–1 at the ice-cap summit Q1207 to 46 mmw.e.d-¹ at the lowermost site Q1201 (Table 1). The mean rate of the seven sites was 30 mm w.e.d–1. The rates were greater down-glacier in general, but the relationship to elevation is not simple (Fig. 2). The melt rate is relatively less sensitive to elevation from about 400 to 700ma.s.l. (e.g. same rates at Q1202 and Q1204), and more sensitive to it from 700 to 1000 ma.s.l. (e.g. -10.5 mm w.e.d^–1 (100 m)^–1 between Q1203 and Q1205) as compared to the mean gradient for the entire elevation range (-4.7 mm w.e.d^–1 (100 m) ^–1 between Q1201 and Q1207).

Table 1. Surface melt rates, horizontal and vertical ice velocities measured at sites Q1201–Q1207. Elevations, measurement periods and surface conditions based on in situ visual observations are listed for the sites

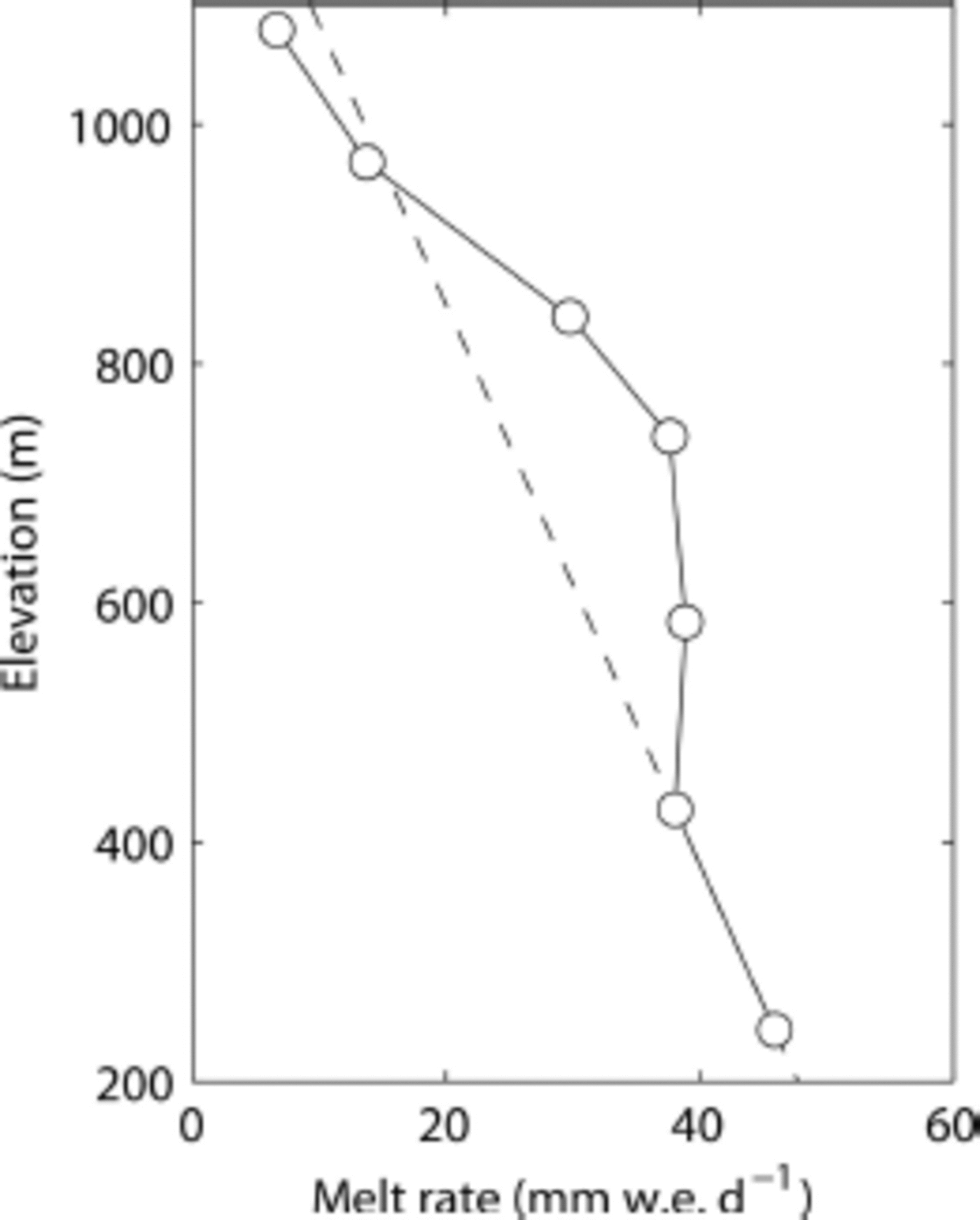
Fig. 2. Mean melt rate at Q1201–Q1207 measured over the periods indicated in Table 1 . The dashed line is the extrapolation of the line connecting the data at Q1201 and Q1202.

3.2. Ice velocity

Horizontal and vertical components of the ice motion are summarized in Table 1, and flow vectors are shown in Figure 1c. Ice flows faster in the middle part of the survey route, where ice is expected to be thick. The greatest horizontal velocities were observed at Q1203 (67.5 mmd^–1) and Q1204 (69.0mmd–¹), and from that region the velocity progressively decreases down- and up-glacier. Flow velocity was only 4.0 mmd^–1 at the lowermost site Q1201 ~500 m from the terminus. Vertical ice motion was downward except for Q1201, where ice emerged at a rate of 0.9 mm d^–1.

The continuous GPS measurement at Q1203 has shown significant ice velocity variations within the range 36–94 mmd^–1, equivalent to 50–140% of the mean velocity (Fig. 3). The variations were diurnal, with minimum and maximum velocities in early morning and late afternoon, respectively. More detailed discussion on the timings of the velocity peaks is difficult as the GPS positioning is not accurate enough. The diurnal variations were clearly recognized until 23 July, but became more irregular for the rest of the period. The daily mean air temperature and its range of variation at Qaanaaq Airport were relatively smaller during the latter half of the observation period.

Fig. 3. Horizontal ice velocity variations at Q1203 and daily mean temperature with its variation range measured at Qaanaaq Airport.

3.3. Ice thickness and bed elevation

Ice thickness, bed and surface elevations were obtained by the ice radar and kinematic GPS measurements along the survey route (Fig. 4). Mean ice thickness along the route was 120m. Ice was thickest (165 m) at 3.2 and 4.4 km from the interior of the ice cap (Fig. 4a), where the bed deepens locally (Fig. 4b). Relatively large bedrock bumps and depressions (amplitude of several tens of metres) are observed in the middle reaches of the ice cap. These irregular bed geometries affect the surface elevation, as represented by a small surface bulge above a bedrock bump at 5.9 km from the summit.

Fig. 4. (a) Ice thickness and (b) surface and bed elevations along the survey route shown in Figure 1c. Ice thicknesses and bed elevations after the ice radar measurements are indicated by (*).

4. Degree-Day Analysis

The temperature record at Qaanaaq Airport (Fig. 5a) was utilized to estimate total summer melt at our measurement sites by the degree-day method. First, daily mean temperature at the measurement sites over summer 2012 was calculated by assuming a temperature lapse rate of -7.80 × 10^–3 K m^–1 (results for Q1201 and Q1207 are shown in Fig. 5b). This lapse rate was calculated from temperatures at Qaanaaq Airport and SIGMA-B during the period of our melt measurement (20-29 July 2012). The temperature series were then used to compute the positive degree-days (PDD) over the melt season (Fig. 5b). Daily melt expected for one degree of positive daily mean temperature (1 Kd), so-called degree-day factor k, was obtained at each elevation of the measurement sites as

(1)

where M(z) and T_m(z) are observed melt during the field study period and estimated mean temperature over a time period At = 1 day, respectively, at elevation z Total melt over the 2012 summer melt season was estimated by

(2)

Fig. 5. (a) Daily mean temperature measured at Qaanaaq Airport for 2010 (blue), 2011 (green) and 2012 (red). (b) Daily mean temperatures (solid lines) and PDD (dashed line) computed for Q1201 (red) and Q1207 (blue). Shaded bands indicate the field study period in 2012.

where suffix t denotes the total values for the whole summer melt season. The computations were performed for the elevations of the measurement sites, and the results are summarized in Table 2 and Figure 6. The degree-day factor at the lower two sites is 5.4-5.5 mm w.e. K–¹ d–¹, which are lower bounds of the previously reported values for an ice surface (Hock, 2003). The factors are greater at Q1203-Q1205, with a peak value of 8.3 mm w.e. K–¹ d–¹ at Q1204 (739ma.s.l.). The degree-day factor is smaller at the upper two sites (Q1206 and Q1207), where the ice-cap surface was covered with a snow layer.

Table 2. PDD over the study period and for the year 2012 (PDD_t), positive degree-day factors (k) and total melt estimated for the summer melt season in 2012 (M _t) at sites Q1201–Q1207

Fig. 6. (a) PDD (•), degree-day factors (*) and (b) total melt amount at Q1201–Q1207 computed for the entire summer melt season in 2012. Blue line in (b) is the brightness intensity of the ALOS PRISM image (25 August 2009; see Fig. 1) along the survey route.

5. Numerical Modelling

5.1. Model

To investigate ice flow and temperature conditions of QIC, a thermomechanically coupled finite-element glacier model was applied to the longitudinal cross section of the ice cap along the survey route. The aim of the modelling was to compare the measured ice velocities with those diagnosed from the present geometry and climate conditions. Also of interest was basal temperature, which is relevant to the diurnal ice velocity variations observed at Q1203.

The model is based on the previously developed two-dimensional ice flow model (Sugiyama and others, 2003), which is coupled with a thermodynamic model in this study. Taking x- and z-coordinates in the along-flow and vertical directions, momentum and mass conservation equations in the x–z plane are

(3)

(4)

and

(5)

where _ij (i,j = x,z) are components of the Cauchy stress tensor, ρ = 910kgm^–3 is the density of ice, g=9.81 ms–² is the vertical component of the gravitational acceleration vector and u_x and u_z are the horizontal and vertical components of the velocity vector. We link the stresses in

Eqn (3) and (4) to the strain rate via the constitutive equation given by Glen’s flow law (Glen, 1955)

(6)

where e _ij and τ_ij are the components of the strain-rate and deviatoric-stress tensors, respectively, and τ_e is the effective stress. We assume the flow-law exponent n = 3 and the rate factor A is a function of T′, ice temperature relative to the pressure-melting point T_m (e.g. Greve and Blatter, 2009).

(7)

(8)

The values used for the constant A₀, activation energy Q, gas constant R, ice melting point at ambient pressure T₀ and its pressure (p) dependence /3 are listed in Table 3. The steady-state

(9)

Table 3. Parameter values used in the numerical model. Values are from Greve and Blatter (2009)

where c is the specific heat capacity and #e is the conductivity of ice with the values listed in Table 3.

The modelled domain was discretized into 800 triangle elements (Fig. 7a) to solve Eqns (1-4) for ux, uz and Eqn (9) for Twith the finite-element method. The horizontal resolution of the velocity field was 100 m, and the vertical resolutions were less than several metres near the glacier bed and 10-15 m near the surface. The resolutions of the temperature field were twice as coarse as those for the velocity. This is because linear triangle elements were used for the temperature field, whereas quadratic elements were applied for the velocity field. To solve the velocity field, a stress-free boundary condition was applied to the upper surface and zero displacement was assumed at the bed. We also assumed horizontal velocity is zero at x=0. For the temperature field computation, surface temperature Ts was prescribed by

(10)

Fig. 7. (a) Finite-element mesh used for modelling the longitudinal cross section of QIC. (b) Ice flow vectors and (c) temperature distribution computed by the numerical model.

where Tref=-8.0°C is annual mean temperature in 2012 measured at Qaanaaq Airport (z _ref=16m). We took = -4.42 x 10–³ K m^–1 for the temperature lapse rate, which was calculated from air temperature records from July 2012 to June 2013 at Qaanaaq Airport and SIGMA-B. Geothermal heat flux into the basal boundary was assumed to be 50 mWm-², which is a value suggested for this region (Greve, 2005).

We first solved the ice dynamics equations for a velocity field. The velocities were then used to compute a temperature field, and the velocity computation was subsequently updated by the temperature using Eqn (7). When ice temperature reached the pressure-melting point, temperature was kept constant at this value and melting/freezing processes were not taken into account. This iteration was repeated until the velocity and temperature fields converged.

5.2. Model results

Modelling results show ice velocity maxima (up to 6m a^–1) in the lower middle reaches of the glacier over the relatively steep surface (Fig. 7b). Ice motion is slow in the upper reaches, where surface velocity is <2.5 ma^–1 within 3000 m of the ice-cap summit. Ice temperature is within the range –13 to –6.5°C (Fig. 7c). The location of the greatest ice motion is influenced by the temperature field, because relatively warm ice in the lower reaches favors deformation.

The magnitude of the computed velocity is significantly smaller than the measurements (control experiment in Fig. 8a). For example, the modelled surface horizontal velocity is 5.9 m a^–1 at Q1203, whereas field measurements showed 24.6ma^–1 at the same location. The measured summer velocity is possibly greater than the annual mean, but the discrepancy is very large. Sensitivity tests were performed to investigate the influence of uncertainties in the geothermal heat flux and ice thickness. The surface velocity increases by taking a greater geothermal heat flux (60mWm^–2) (experiment 1: Au = +11% on average), and by assuming the glacier is 10m thicker than estimated in Figure 4 (experiment 2: Δu = +45% on average) (Fig. 8a). However, the effect is too small to explain the inconsistency with the field data. The changes in glacier bed temperature are also small, i.e. T= +0.6°C and +0.3°C for experiments 1 and 2, respectively (Fig. 8b).

The most likely reason for the inconsistency with the field data is that the modelled temperature is too low. The computed glacier bed temperature is below -6.5°C (control experiment in Fig. 8b), which also contradicts the diurnal ice flow variations observed at Q1203. The diurnal velocity variations strongly suggest the changes in the basal velocity, i.e. part of the glacier bed is melting and lubricated by diurnal input of surface meltwater.

Fig. 8. (a) Horizontal components of the surface ice motion. Black curve is computed with the numerical model with the standard conditions described in the text (control experiment). Green, blue and red curves are computed with the assumptions geothermal heat flux = 60 mWm^{– 2} (experiment 1), + 10m ice thickness (experiment 2) and T _ref = –2.0°C, (experiment 3), respectively. Observational data are indicated by the asterisks. (b) Surface (dashed) and bed (solid) temperature computed with the numerical model. Experimental conditions for the black and coloured curves are as in (a).

To investigate the influence of temperature on the ice dynamics, an additional experiment was performed by assuming an annual mean temperature ╤ _ref =-2.0°C at the reference elevation. The model slightly under/overestimates the observations in the upper/lower reaches, but relatively good agreement was achieved (experiment 3 in Fig. 8a). Glacier bed temperature reaches the pressure-melting point in the lower reaches at x= 5800-7500 m, which is consistent with the observed diurnal flow variations. Overall, the model better reproduces the observations under an unrealistically higher surface temperature than the actual air temperatures.

6. Discussion

6.1. Summer temperature and melt conditions in 2012

The melt rate obtained near the terminus of Qaanaaq Gletscher (46 mm d^–1 at Q1201) is comparable to the values reported for mid-latitude glaciers. For example, mean melt rate within the lower 1 km of Rhonegletscher, Switzerland (2200–2350m a.s.l.), from July to September was reported to be 56 mmw.e. d^–1 (Sugiyama and others, 2011). At 4.5 km from the terminus of Glaciar Perito Moreno, Southern Patagonia Icefield (360 ma.s.l.), mean melt rate from November to March was 55 mmw.e. d^–1 (Stuefer and others, 2007). Climate conditions on QIC during such an intensive melt period were analysed by air temperature recorded at Qaanaaq Airport. Daily mean temperature variations show that our study period corresponds to the warmest period in the year (Fig. 5a). Mean temperature from 18 to 29 July 2012 was 10.2°C, and one of the peak temperatures of the year was observed on 27 July. In July 2012, an extraordinary high-temperature event hit Greenland and melt occurred over nearly the entire surface of the ice sheet (Nghiem and others, 2012). However, temperature at Qaanaaq Airport shows no clear indication of this melt event, and the summer temperature in 2012 differs little from those in 2010 and 2011. Summer (June/July/August) mean temperature in 2012 (6.1°C) was higher than that in 2010 by 0.3°C, but lower than that in 2011 by 0.6°C. Therefore, the observed melt rates represent midsummer melt conditions on QIC over the last several years.

6.2. Enhanced melt on dark surface

The degree-day factors computed at the measurement sites show an interesting dependence on elevation (Fig 6a). The greater degree-day factors in the middle reach of the ice cap can be attributed to ice surface conditions. The ice surface over the region including Q1203–Q1205 was covered by dark materials, and thus absorbed more solar radiation as a result of low albedo. The spatial variation in surface reflectance was clearly observed by in situ visual observations (Fig. 9). Moreover, the brightness intensity of the ALOS (Advanced Land Observing Satellite) PRISM (Panchromatic Remote-sensing Instrument for Stereo Mapping) satellite image acquired on 25 August 2009 (Fig. 1c) gives a quantitative measure of the surface reflectance along the survey route (Fig. 6b). The intensity decreases up-glacier of the terminus and shows consistently smaller values between Q1203 and Q1205. The smaller degree-day factors at the upper two sites (Q1206 and Q1207) can be explained by higher albedo due to the snow cover.

Fig. 9. Photographs showing (a) clean and (b) dark ice surface conditions on QIC. Photographs were taken (a) at Q1201 viewing up-glacier on 18 July 2012 and (b) at the middle reach of Q1203 and Q1204 viewing down-glacier on 22 July 2012.

Darkening of the glacier surface has been reported in many glaciers in the world (e.g. Takeuchi and others, 2001; Oerlemans and others, 2009), including marginal regions of the Greenland ice sheet (e.g. Van de Wal and Oerlemans 1994; Wientjes and Oerlemans 2010; Wientjes and others, 2011). Such changes in ice surface conditions result in melt increase due to the reduction in albedo, and thus accelerate mass loss of glaciers and ice sheets. A field study has shown that the dark appearance over QIC is caused by materials consisting of mineral dust, snow algae and other organic matter (Takeuchi and others, 2013). The degree-day factors obtained in this study confirm the link between this darkening surface and melt rate increase. For example, the factor at Q1204 was 50% greater than that at Q1202, suggesting that the ice in the dark regions melts 50% more than the magnitude expected if the surface was clean, as it is in the lower reaches. Because of the recent negative mass balance in the Greenland coastal regions (Bolch and others, 2013), ablation areas are expanding and ice surface is exposed for longer periods in the summer. This is a favorable condition for biological activities because they are more active on a bare ice surface rather than snow (Takeuchi, 2013). Thus, further darkening and melt rate increases are likely to occur over the GICs and ice-sheet margins in Greenland.

6.3. Ice flow and temperature conditions

Diurnal flow velocity variations at Q1203 (Fig. 3) imply that surface meltwater drained to the bed through cold ice and enhanced basal ice motion. Thus, at least a part of the glacier bed is melting in this region. This observation contradicts the wholly frozen ice temperature computed by the numerical model (Fig. 7c). Moreover, the measured surface velocities are substantially greater than those computed by the model (Fig. 8a). These observations suggest that the modelled ice temperature is significantly lower than the actual temperature, and some important thermodynamical processes are missing from the model.

Discrepancies between the modelling results and observational data have previously been reported for other Arctic glaciers. Blatter and Hutter (1991) applied a thermomechanical glacier model to Laika Glacier, Coburg Island, Canadian Arctic (75850⁰ N, 79810⁰ W). In contrast to the borehole measurements showing the existence of a temperate bed in the ablation area (Blatter and Kappenberger, 1988), the model predicted that the glacier is entirely cold. Similar results were obtained for John Evans Glacier, Ellesmere Island, Canadian Arctic (798400 N, 74800⁰ W) (Bingham and others, 2008), as well as for McCall Glacier, Alaska, USA (79817⁰ N, 143850⁰ W) (Pattyn and others, 2005).

Several mechanisms have been proposed for the inadequate modelling results in these glaciers, which are located in similar latitude and elevation ranges. First, the ice temperature near the surface is not simply controlled by air temperature (Blatter and Hutter, 1991; Bingham and others, 2008). A large amount of latent heat is generated when meltwater percolates and refreezes in a cold firn layer. The insulation effect of a firn layer also plays a role in keeping the near-surface ice warmer than the annual mean air temperature. Second, surface meltwater transports sensible heat into a glacier if it penetrates into englacial and subglacial environments (Bingham and others, 2008; Wohlleben and others, 2009; Phillips and others, 2010). The diurnal velocity variations confirm penetration of surface water to the bed of QIC, and we also observed water-filled crevasses in the accumulation area. Finally, recent changes in ice thickness may have influenced the ice temperature field. The ice temperature may not be in equilibrium with the present geometry, so warm ice remains as a remnant of earlier thicker ice conditions. These complex processes must be investigated further in the field and accurately taken into account in the model to better simulate the actual flow velocity and temperature fields of QIC.

7. Conclusion

To better understand the GICs in Greenland, which are physically disconnected from the ice sheet, we carried out initial field observations on QIC. Surface melt rate, ice flow velocity, and ice thickness were measured along an 8km survey route from the ice-cap summit to the terminus of an outlet glacier.

Melt rates were clearly influenced by dark materials covering the middle elevation range of the ice cap. The degree-day factor was greater on the dark surface (8.26mmw.e. K^–1 d^–1 at 739 ma.s.l.) than on a clean surface (5.44mmw.e. K^–1 d^–1 at 427 ma.s.l.). This result strongly suggests the important role of darkening ice surface in the melt increase on Greenland’s GICs. Ice velocity showed diurnal variations, indicating surface meltwater is affecting the basal ice motion. Meltwater should have been routed through ice to the bed, although surface annual mean air temperature is far below the melting point (below –8°C at the terminus). Ice-cap surface and bed geometries measured in the field were used to compute ice velocity and temperature using a numerical glacier model. The model assumed that ice surface temperature is equal to the annual mean air temperature, and the ice cap is in equilibrium with present climate and geometrical conditions. Computed ice temperature was too low to reproduce the observed ice velocity, implying the important role of latent and sensible heat transport by meltwater as well as recent changes in the ice thickness. These processes will have to be accurately taken into account in the model to understand the current status and future evolution of the GICs in Greenland.