Heavy rain on snow cover

Abstract

Heavy rain on snow often leads to disastrous damages in torrent watersheds. In January 1998 a project was started to investigate “runoff and infiltration characteristics of different alpine soil/vegetation units under snow cover”. One aim was to determine the runoff rates from snow-covered, differently cultivated soil/vegetation units (pastures, dwarf-shrub stands, forests), especially under conditions of sparse snow cover and frozen soil. Differences in runoff formation between artificially snowed skiing areas and plots with natural snow cover were also of interest. Heavy rain (intensity 100 mm h^–1) was simulated on four plots by using a transportable spray irrigation installation. The investigations showed runoff coefficients of 0.4–0.7. The lowest runoff values were found where the soil under snow cover was not frozen, but even on these stands the runoff coefficient exceeded 0.4. Snow depth and runoff delay are strongly correlated (R² = 0.8). An increment in snow of 10 cm is followed by a runoff delay of 3.6 min. Divergences from this coherence are due to the composition of the snowpack, especially in case of artificial snow. This result is encouraged by runoff simulations performed for the irrigated plots by use of a hydrological model.

Introduction

During winter or early spring in the Alps, influx of warm air combined with heavy rain or long-term rainfall often causes floods or torrents. A number of international researchers have investigated the topic of snowmelt and runoff out of snow cover (Marsh and Woo, 1984; Johnsson and Lundin, 1991; Bloschl and Kirnbauer, 1992; Stadler, 1996; Stadler and others 1996). It is more difficult to find information about the reaction of torrent catchments to rain-on-snow events.

In order to discuss this theme a project “Runoff and infiltration characteristics of different Alpine soil/vegetation units under snow cover” was started. The main objective of this study was to determine the influence of snow cover, vegetation (pastures, dwarf-shrub stands, forest stands) and underlying soil conditions on runoff generation in case of heavy rainfall. Differences in runoff formation between hill slopes covered with natural and with artificial snow were also to be investigated.

Study Area and Methods

The skiing area on the Patscherkofel near Innsbruck, used during the Olympics in 1964 and 1976, was chosen for the simulation of heavy rainfall on snow cover. For this purpose a transportable spray irrigation installation with a rainfall intensity of approximately 100 mm IT¹ was used. Four research plots were investigated: two were pastures used for skiing in winter, one a slope with artificial snow, the second a slope with natural snow; the other two plots were a rhododendron stand and a forest stand, each measuring 15 m × 5 m (see Table 1). A detailed description of the irrigation procedure and the spray irrigation installation was given by Markart and Kohl (1995). The irrigation experiments took place twice, at the end of March 1998 and again in early spring 1999, with different conditions of the snowpack. Additional irrigation experiments were carried out in autumn 1998 and late spring 1999, in order to assess runoff characteristics without snow cover and quantify the influence of grazing intensity on runoff behaviour.

Table 1 Rain-plot characteristics

Changes in soil water content during the irrigation experiments were measured by time-domain reflectometry (TDR) steel rods (Soilmoisture Trase (moisture measuring system), 20 cm) inserted horizontally at different points in a soil depth of 5 and 15 cm. Soil temperature sensors were placed at the same depth. Additional temperature sensors were used to determine the temperature of snow and irrigation water. Snow depth, density of snow, grain-size and layers were measured in snow-cover profiles. Snow wetness profiles were measured before and after the irrigation experiments using snow dielectric devices (Denoth and Wilhelmy, 1989). During the irrigation, snow moisture was observed continuously at 10–20 cm depth by means of a vertical inserted snow dielectric device of the same kind as mentioned before. Additional measurements included meteorological observations by use of a transportable automatic weather station, soil physical characteristics (pore volume and distribution, grain-size distribution, organic matter, saturated hydraulic conductivity), biomass and vegetation surveys.

By means of a hydrological model the observed runoff should be reproduced as accurately as possible. As a result, conclusions can be drawn about the essential hydrological processes in case of heavy rain on snow cover.

Results of the Experiments

Table 2 shows the runoff characteristics of the different research plots under wintry conditions. The 1998 snow depth varied to a great extent. Rain plot 1 (RP1), a rhododendron heath, was covered with a snowpack 66 cm deep. The artificial snow cover on plot 2 attained almost 90 cm, while snow depth on the slope with natural snow reached only 20 cm, and an average of 15 cm was measured at the forest stand. Snow cover in the measurement period 1999 was clearly higher. Soil moisture sensors (TDR) and soil temperature sensors indicated frozen soil on all plots except RP1 and RP4 in 1998. Soil frost causes different infiltration behaviour.

Table 2. Runoff characteristics: simulation of heavy rainfall on snow cover

Figure 1 gives an example of an unfrozen soil with high initial water content and a slight increase in soil moisture during the irrigation experiment, nearly to the point of saturation. The characteristic of the surface runoff curve, especially the maximum runoff value, is strongly influenced by the soil conditions. After a typical runoff it increases until infiltration and runoff reach an equilibrium. After irrigation has stopped, water continues to seep through the snowpack. Runoff gradually decreases. At RP3 (Fig. 2) soil moisture remains constant at a low level. Due to reduced free pore volume in the frozen soil, maximum runoff reaches a considerably higher value. The worst infiltration features were found on the skiing ground with natural snow. The quantified total runoff coefficient was about 0.6 in case of a 20 cm snow blanket and 0.5 when the snow cover was 94 cm. During the equilibrium state, maximum runoff coefficients of about 0.7 were observed. Concerning runoff quantity, RP2 reacted similarly to RP3. On the skiing ground covered with artificial snow of high density (87 and 104 cm), maximum runoff coefficients of 0.6 (1998) and 0.5 (1999) were observed. TDR data and soil temperature at RP2 and RP3 indicated frozen soil in both 1998 and 1999. The best infiltration characteristics were observed on the rhododendron heath and the forest stand with non-compacted snow and unfrozen soil.

Fig. 1. Surface runoff under snow cover: monitoring of soil and snow liquid-water content during irrigation experiment (secondary y axis), RP1, 30 March 1998; starting-point and end of irrigation are marked by vertical lines.

Fig. 2. Surface runoff under snow cover: monitoring of soil and snow liquid-water content during irrigation experiment (secondary y axis), RP3, 30 March 1999; starting-point and end of irrigation are marked by vertical lines.

In rain experiments during the vegetation period (without snow cover) the smallest equilibrium runoff coefficients occurred at RP4 (<0.1; forest stand). The high runoff values at RP4 during the second winter experiment (equilibrium runoff = 74% in 1999; cf Table 2) were therefore surprising. According to the results of other studies (Stadler, 1996; Stadler and others, 1996), the high runoff coefficients are mainly due to frozen soil. Drainage is strongly influenced (but not inhibited) by soil frost (Johnsson and Lundin, 1991).

Figure 3 gives an overview of the runoff results achieved from all irrigation experiments on snow cover (snow depth is related to the secondary y axis). Total runoff is 26–60%, and maximum runoff 42–74%. These results prove that neither total runoff nor maximum runoff depended on snow depth, which was mainly due to the fact that “ripe” snowpacks were irrigated (the water-holding capacity was reached before irrigation started). The observed runoff delay was 7–44 min after the start of the irrigation experiment (Fig. 4).

Fig. 3. Total and maximum surface runoff under snow cover: irrigation experiments on four rain plots, 1998 and 1999: secondary y axis indicates snow depth at time of irrigation.

Fig. 4. Runoff delay and time till runoff attains equilibrium: irrigation experiments on four rain plots, 1998 and 1999; secondary y axis shows snow depth at time of irrigation.

While shallow snow blankets lead to an early beginning of runoff, deep snowpacks show a considerable delay. Snow depth and runoff delay are strongly correlated (R² = 0.8; Fig. 5). An increment in snow of 10 cm is followed by a runoff delay of 3.6 min. The longest delay was measured at RP2 (artificial snow). The mechanically compressed natural snow cover on RP3 with a comparable depth formed runoff about 15 min earlier. These divergences seem to be mainly due to the composition of snowpack, especially in case of artificial snow. Such effects are also reported in other studies (see Marsh and Woo, 1984; Johnsson and Lundin, 1991; Stadler and others, 1996).

Fig. 5. Snow depth vs runoff delay: irrigation experiments on four rain plots 1998(×) and 1999 (+).

Hydrological Model

In the model the snowpack of the plot is idealized as a porous medium which consists of a main body that is unsaturated with respect to liquid water, and a thin saturated layer at the soil/snow interface. It is assumed that vertical flow prevails in the unsaturated zone, while water reaching the saturated zone either infiltrates into the soil or moves downhill as basal flow, eventually producing snowpack runoff This assumption is correct only for homogeneous snowpacks but is probably a good approximation for any natural snow cover (Colbeck, 1974). According to this idealization of the process, the model consists of two main components (Fig. 6).

Fig. 6. Flow processes on a snow-covered hill slope during heavy rainfall, as idealized by the hydrological model.

Model component for simulating vertical How

This model component accounts for liquid-water flow, heat propagation and phase changes in order to simulate the transport of mass and heat in vertical direction. Water-vapour diffusion is neglected.

Liquid-water flow can be described mathematically by using two basic equations, the equation of continuity and Darcy’s law. According to Akan (1984), the equation of continuity for one-dimensional flow is

(1)

where t is time, n is the snow porosity, p is the density of liquid water, S is the degree of saturation, z is the vertical distance positive upward, u_w is the superficial velocity and M_w is a source term which represents the net mass of liquid water produced because of phase change per unit snow volume per unit time. The superficial velocity u_w can be derived from Darcy’s law generalized for unsaturated non-steady flow:

(2)

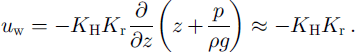
K_R is the saturated hydraulic conductivity, K_r is the relative conductivity, p is the liquid water pressure, and g is the gravitational acceleration. Since the capillary forces, resulting from differences in the liquid water pressure p, are usually two to three orders of magnitude lower than those of gravity (Colbeck, 1971), the pressure gradient ∂p/∂z was neglected in the model, and Darcy’s law was reduced to the gravitational form.

The saturated hydraulic permeability was estimated from snow parameters (grain-size d, density 7 using the formula of Shimizu (1970). This formula was developed for snow grains which are smaller than 1 mm. However, it has been used for larger grains as well (Colbeck, 1978). The relative conductivity K_r was determined as a function of the effective liquid saturation, applying the relationships given by Colbeck and Anderson (1982). The relevant formulas are summarized inJordan (1991).

The initial conditions required to solve the differential equations describing the flow of mass and energy in the model are the initial distributions of snow density, liquid-water content and snow temperature. Since snow metamorphism was neglected, the distribution of snow grain-size was assumed to be constant throughout the irrigation experiment.

The upper boundary conditions during the experiments are described by the mass flow (observed rainfall rate) and energy flow at the snow surface. The latter was derived from observations of air temperature, rain intensity and wind speed using the approach given by Anderson (1973).

Model component for simulating basal flow

The saturated zone is assumed to be isothermal at 273 K, and the basal flow is fully saturated with respect to liquid water. According to Akan (1984), the equation of continuity and Darcy’s law written for a one-dimensional saturated flow in the x direction can be combined to yield

(3)

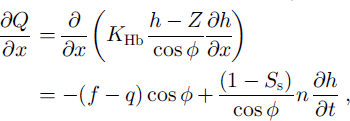
where h is the piezometric head, Z is the ground elevation, q is the rate of seepage of liquid water from the unsaturated zone, S_s is the degree of saturation immediately above the saturated zone and φ is the slope of the plot. In the model the saturated permeability K_Hb for basal flow at the soil/snow interface was assumed to be different from that within the snowpack (K_H vertical flow). It was determined by calibration. For the rate of infiltration f, two different assumptions were made, depending on the soil conditions:

(4)

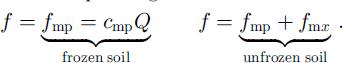
f is assumed to be proportional to the basal flow Q if the ground is frozen, cmp is the percentage of Q that is lost per metre flow length due to flow into macropores and large openings bypassing the frozen-soil matrix. If the ground is not frozen, there is additional infiltration into the soil matrix f_mx, which is assumed to be a constant rate (saturated soil due to preceding meltwater infiltration).

Model limitations and technical realization

In the model the snowpack is considered as a homogeneous porous medium with constant hydraulic properties throughout the irrigation experiment. Snow metamorphism caused by the infiltrating rainwater is neglected. Capillary forces, ponding and lateral flow above ice layers or the development of flow channels, which may have significant influence on water movement within the snowpack, cannot be simulated.

The mathematical problem described by the equations above was solved numerically by using a finite-difference scheme which required a spatial and temporal discretization of the process. Therefore the snowpack was subdivided into 15 separate snow columns each consisting of 10 layers (model component 1; see Fig. 6). To allow simulation of basal flow, the lowest layer of each column was linked to the neighbouring downstream element (model component 2). The programming was done in Fortran 77. As a framework for modelling, the “Modular Modeling System” (Leavesley and others, 1996) was used. This integrated software system substantially facilitated modularization and calibration of the model. It also provided for the necessary pre- and postprocessing tools.

Simulation results

The snowpack state at the beginning of the irrigation experiment was described by several parameters observed or estimated at the plot (snow depth, snow water equivalent, liquid-water content, snow temperature). The water-holding capacity of the snowpack (i.e. the minimum liquid level to which a snow cover can be drained regardless of the imposed suction) was assumed to be around 5%.

Many of the investigated snowpacks showed inhomogeneities (ice layers, high-density layers) with hydraulic properties that could not be described properly by snow density and grain-size. Therefore it was decided not to use the observed values of grain-size for model parameterization, but to find an average grain-size resulting in good agreement between simulated and observed runoff delays. This grain-size, determined by calibration, was termed “hydraulically effective grain-size 4e”. It can be interpreted as the mean grain-size of an ideal homogeneous snowpack that has the same effect on runoff delay as the inhomogeneous snowpacks observed on site. Low values of dhe indicate either fine-grained snow or inhomogenities within the pack. Further model parameters that needed to be calibrated were the hydraulic conductivity of the saturated layer K_Hb and the soil infiltration parameters f_mx and c_mp. While K_Hb mainly influences the increasing section of the observed runoff curve, the infiltration parameters control the simulated snowpack runoff during the equilibrium state.

From Table 3 it can be seen that the lowest values of d_he were found for RP2. This is certainly due to the inhomogeneous profile of these snowpacks, with highly compressed layers of artificial snow causing a significant delay in runoff. For the hydraulic permeability K_Hb of the saturated zone, values on the order of 0.01 m s⁻¹ were found. The highest infiltration rates were determined for the winter 1998 experiments at RP1 and RP4 (unfrozen soil). Figure 7 shows simulated and observed graphs of irrigation, snow ex-filtration (i.e. seepage from the unsaturated into the saturated layer), soil infiltration and snowpack runoff for RP3 and RP4 during the winter 1999 experiments. The snow profiles of RP3 indicated a rather uniform snowpack with no ice layers and with grain-sizes of 2–4 mm. Using a value of 4 e = 3 mm, very good agreement was obtained between simulated and observed runoff values. The snow profile of RP4 showed similar values of grain-size but also two ice layers 6 and 47 cm above ground. As can be seen from Figure 7, the model did not reproduce the observed runoff curve satisfactorily. Obviously the vertical movement of water down the snowpack was delayed by the presence of ice layers in the pack. However, it is likely that during the experiment the ice layers became permeable and flow channels developed, accelerating the flow of water through the pack. This would explain the fast decrease in runoff immediately after irrigation was stopped. Since the model assumes constant hydraulic properties throughout the experiment, it did not perform well in this particular case.

Table 3. Predetermined and calibrated parameters of the hydrological model

Fig. 7. Simulation of the flow processes at RP3 and RP4.

Summary and Outlook

The amount of surface runoff observed during the rain-on-snow experiments depended mainly on whether soil was frozen or not. As drainage is influenced but not inhibited by soil frost, up to 30% of water percolating through snow cover was still able to infiltrate into the soil. The onset of runoff was strongly dependent on snow depth. For the experiments, a 3.6 min runoff delay per 10 cm additional snowpack was calculated. Divergences from this coherence were obviously due to quality and composition of the snowpack. This was confirmed by the results of the hydrological simulation, which showed that especially the highly compressed layers of artificial snow, as well as ice layers in natural snow covers, can increase the delay of runoff significantly.

The relatively simple hydrological model showed good performance for most of the irrigation experiments and allowed the governing flow processes to be identified and quantified during the simulated rain-on-snow events. The model takes into account the initial state of the snowpack (density, liquid-water content, temperature), the snow parameters (grain-size, water-holding capacity) and the meteorological situation (rainfall intensity, temperature and wind speed). To investigate the influence of these conditions on runoff during rain-on-snow events will be one of the future tasks and possible applications of the model.