Introduction
The ground coser of the tundra and taiga regions of Arctic and sub-Arctic Alaska consists of lichens, mosses, sedges, and grasses. This vegetation forms a hummocky carpet with microrelief ranging from 0.1 to 0.5 m (Reference BeschelBeschel, 1965; Reference Pruitt, Olsen, Hastings and GeddesRadforth, 1965; Reference RadforthRaup, 1965). In particular, sedges (Eriophorum L. and Carex L.) (Reference Chapin, van Cleve and ChapinChapin and others, 1979; Reference Walker, Everett, Webber and BrownWalker and others, 1989; Reference Trabant and BensonViereck and others, 1992) form distinctive tussocks that project well above the surrounding terrain. Frost boils, polygons, and other permafrost features add to the microrelief (Reference Viereck, Dyrness, Batten and WeizlickWalker and others, 1980). For simplicity we here use the term tussock to refer to all mounds formed by vegetation.
Because snow cover in the Arctic and sub-Arctic is thin, the microrelief is often a substantial fraction of the total snow depth. As a result, it has a pronounced effect on the structure and thermal characteristics of the snow and underlying ground. Reference Combarnous and BoriesDesrochers and Granberg (1988), Reference Gold and LachenbruchGranberg (1988), Reference Granberg and SennesetNelson and others (1988), and Reference RaupSeppälä (1990) have documented these effects for topographic features with scales of ten to hundreds of meters, but little has been published on the effects due to microtopography. As a practical matter, however, microtopography makes it difficult to assign engineering and thermal parameters to a thin snow cover. Yet it is well recognized that the thermal balance of the ground is strongly dependent on snow conditions (Reference BenninghoffBenninghoff, 1965; Cold and Lachenbruch, 1973; Reference Nelson, Outcalt, Hinkel, Murray, Murray and SennesetNicholson and Granberg, 1973).
In this paper, we present a series of measurements made at lour locations in Alaska. Temperature and heat flow were measured hourly in the snow and ground at two tundra and two taiga sites with typical vegetation and microrelief. From the measurements we document the effect of microrelief on the snow/ground interface temperature and heat flow.
Background
The tundra and taiga snow covers of Alaska have been described by Pruitt (Reference Nicholson and Granberg1970, Reference Pruitt1984), Benson (Reference Benson1967, Reference Benson1982), Reference Sturm and JohnsonTrabant and Benson (1972), Reference SturmSturm and Johnson (1991), Reference SeppalaSturm (1991) and Reference Benson and SturmBenson and Sturm (1993). Both snow covers are relatively thin (~0.4 and 0.7 m deep respectively) and exposed to strong temperature gradients that cause the snow to metamorphose into depth hoar. They differ in two important respects:
-
Tundra snow is continuously reworked by the wind, resulting in the formation of high-density wind slabs, large drift deposits and surface sastrugi. Taiga snow is rarely affected by the wind.
-
Trees cause considerable redistribution and thermal disturbance in the taiga snow (Pruitt, Reference Nicholson and Granberg1970, Reference Pruitt1984; Reference SturmSturm, 1992) whereas there are no trees in the tundra to have a similar effect.
Methods
Instrument arrays (Fig. 1) were installed at lour sites (Table 1) and measurements of temperature and heat flow were recorded hourly during the winters between 1989 and 1992. Ten thermistors (VECO Model T32A11, accurate to ±0.05°C) were installed at the ground surface on undisturbed vegetation. They were spaced every 0.15 m along a horizontal line and fell on the top or between tussocks at random. A second thermistor was
Table I. Site descriptions and locations

suspended vertically above each thermistor on the ground, and the entire array was allowed to be buried by snowfall.
Heat flux transducers (HFTs)(International Thermal Instrument Co. Model GHT-1B, accurate to ±0.04 W m −2) were installed near the thermistors. They were oriented horizontally and embedded slightly in the vegetation to improve thermal contact. At two sites (Imnavait and Glenn Creek A), two HFTs were installed adjacent to one another, one on the top of a tussock, the other in a hollow between tussocks. The HFTs wen-painted white to reduce radiation healing, and results reported here do not include periods from early in the

Fig. 1. The thermistor and heat flux transducer array used at each site. Thermistors in the snow were suspended on kevlar thread and allowed to be buried by snowfall
winter when solar heating through the snow might have occurred.
Snow structure and its relationship to the microtopography was examined monthly near each site by excavating trenches in the snow. Prior to excavation, the temperature of the snow/ground interface was measured with thermistor probes. After the trench was opened, the microtopography and lateral variations in the stratigraphy were measured allowing cross-sections accurate to ±0.01 m to be drawn. At the end of the winter a similar trench was excavated through the thermistor array and the final positions of the thermistor and the snow strata in which they were embedded were determined. Microtopography at each site was surveyed in summer to produce maps with contour intervals of 0.025 m.
Results
Snow cover over microtopography
A cross section through the snow cover at Imnavait Creek (Fig. 2) illustrates some typical features:
-
The microtopographic relief and the snow depth are of the same order.
-
The snow cover consists of two components: wind slab and depth hoar.
-
The basal depth hoar and the immediately overlying wind slab arc discontinuous. They pinch out at tussock tops.
-
The temperature of the snow/ground interface varies 10°C and is roughly correlated with the microtopography.
The discontinuous strata form in early winter when the vegetation still contains considerable sensible and

Fig. 2. A cross section through the snow cover at Imnavait Creek, 18 November 1989. Depth hoar is indicated by an inverted “V”; wind slab is indicated by a dot with a line through it. Note discontinuous snow strata that pinch out over tussock lops. In the lower part of the figure, the temperature of the snow/ground interface is shown
latent heat. The first snowfalls settle, are blown, or preferentially melt from the tops and south sides of tussocks. Once exposed, tussocks are warmed more rapidly by solar radiation due to their lowered albedo, further clearing them of snow. This leaves pockets of snow between tussocks that rapidly metamorphose into depth hoar. In the wind-swept tundra, subsequent snowfalls tend to completely fill all the hollows between tussocks and create a nearly level surface. In the taiga, with little wind, the snow surface continues to mimic the underlying microtopography until the snow depth is about twice the microrelief, at which time the snow surface begins to level out.
Temperature at the snow/ground interface
In a previous study (Reference SeppalaSturm, 1991), the temperature of the snow/ground interface was shown to be spatially variable, even beneath snow deposited on level, homogeneous sand. Throughout the winter, differences of 1° to 2°C were common over horizontal distances of 0.5 m. It was hypothesized that differences in soil moisture may have been the cause.
Interface temperatures beneath snow deposited on the natural microrelief at our sites (relief ranging from 0.02 to 0.29 m) were found to vary considerably more than for level substrates. The range in temperature computed from 10 thermistors at the snow/ground interface is

Fig. 3. The range of temperature, as measured at 10 points along a 1.5 m line at the snow/ground interface, Glenn Creek and Imnavait Creek, 1989–90. See Table 1 for site locations and descriptions. Local microrelief was 0.29 m at Glenn Creek, and 0.16 m at Imnavait Creek: maximum snow depth was 0.85 m and 0.18 m, respectively
Table II. Average thermal values for a taiga and a tundra site


Fig. 4.a. Thermistor locations and b, the deviation from the mean interface temperature of a thermistor in a hollow (H1-5) and a thermistor on a tussock (H1-1) at Imnavait Creek. Other pairs of thermistors gave similar results
plotted in Figure 3 for a taiga and tundra site. The 1989–90 winter average temperature range for the two sites was 4.5°C and 7.2°C, respectively. The maximum range (19.1°C) was recorded at the tundra site (Table 2). Average air temperature was similar at both sites, but the microrelief was greater at the taiga site. However, the snow was considerably thicker there as well, thus the range of temperature at the interface was less.
The dominant control on the interface temperature appeared to be the microtopography (Fig. 4). Thermistors located in hollows were consistently warmer than thermistors located on tussocks. Maximum deviations occurred during periods of the lowest air temperatures; for the thermistors illustrated in Figure 4, horizontal temperature gradients exceeding 30°C m−1 were maintained for up to 10 days. In extreme cases adjacent pairs of thermistors (0.15 m apart) differed by as much as 9°C resulting in horizontal gradients exceeding 60°C m–1.
Temperature data from trench studies and longer traverses suggest that the relationship between microtopography and interface temperature holds only over length scales of several meters, with other processes masking the relationship at larger scales. For example, in more than half of our snow trenches, a good inverse correlation ![]() was found between interface temperature and snow depth. Since snow depth and microrelief were usually strongly correlated, good correlations also existed between the interface temperature and the microtopography. In other cases, the interface temperature was better correlated with the thickness of the depth hoar layer. In a few cases, chiefly when measurements were more widespaced, interface temperature was not correlated with any parameter. This was particularly notable in the data taken along a 1 km traverse across Imnavait Creek. On this traverse, the interface temperature and snow depth were measured every 10 m; their coefficient of correlation (r2) was 0.01.
was found between interface temperature and snow depth. Since snow depth and microrelief were usually strongly correlated, good correlations also existed between the interface temperature and the microtopography. In other cases, the interface temperature was better correlated with the thickness of the depth hoar layer. In a few cases, chiefly when measurements were more widespaced, interface temperature was not correlated with any parameter. This was particularly notable in the data taken along a 1 km traverse across Imnavait Creek. On this traverse, the interface temperature and snow depth were measured every 10 m; their coefficient of correlation (r2) was 0.01.
Heat flow on microtopographic highs and lows
Heat flow measured using heat flux transducers (HFTs) was significantly higher from tussock tops than from adjacent hollows. This is illustrated in Figure 5a using data from Imnavait Creek, where the two HFTs were 0.3 m apart and 0.15 m different in height. The ratio of the measured heat flows,

where qt is heat flux over the tussock, and qs is heat flow over the adjacent hollow, is plotted in Figure 5b. The average value of RHFT ranged from 1.4 to 2.1 between 1989 and 1992. Its value at the Glenn Creek site was 1.9 in 1991–92 (the only year for which there are data).

Fig. 5.a Heat flow from a tussock lop (dotted) and an adjacent hollow (solid) measured by heat flux transducers (HFTs) at Imnavait Creek, b. The ratio of these heat flows (RHFT)
The effect of tussocks on heat flow
The effect of tussocks on heat flow can be estimated using a simple model (Fig. 6 inset). In the model, the ground surface is overlain by a horizontal, homogeneous snow-cover of depth hs and thermal conductivity ks. On this surface, there is a step-like tussock of height ht. It is assumed that the tussock is of sufficient width that the heat flow in the center of the tussock can be characterized as vertical and one-dimensional. The underlying ground is homogeneous with thermal conductivity kg, and temperature Tg at a depth hg (sufficiently deep that isotherms are horizontal and parallel). Air temperature Ta is specified. Using these boundary conditions and the solution for thermal conductivity of parallel layers (Combarnous and Bories, 1975), the ratio of the heat flow over the tussock to the heat flow of the surrounding area is

where ![]() equals
equals ![]() ,
,

and
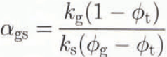
where ![]() equals
equals ![]() ,
,
In Figure 6, RCALC is plotted for tussock heights from 0 to 60% of snow depth using a value of kg appropriate for the Arctic and sub-Arctic, and using average measured values of Ta and Tg (the latter measured 0.4 m below the ground surface). The results are plotted for thermal conductivities (ks) ranging from relatively low conductivity depth hoar (ks = 0.05 W m−1 K−1) to high

Fig. 6. The ratio of heat flow over a tussock to the heat flow over an area without a tussock RCALC calculated using Equation (2). RCALC has been plotted as function of the ratio of the tussock height to the total snow depth ![]() for snow thermal conductivities ranging from depth hoar (0.05 W m −1 Κ−1, Reference Sturm and JohnsonSturm and Johnson, 1992) to wind slab (0.80 W m −1 Κ −1). The inset shows the geometry of the tussock and symbols used in the text.
for snow thermal conductivities ranging from depth hoar (0.05 W m −1 Κ−1, Reference Sturm and JohnsonSturm and Johnson, 1992) to wind slab (0.80 W m −1 Κ −1). The inset shows the geometry of the tussock and symbols used in the text.
conductivity wind slab (ks = 0.80 W m−1 Κ−1). RCALC is equal to or greater than 1 for all choices of input parameters. For tussock heights observed at our sites ![]() , modeled heat flow from the tussock varied from 1.1 to 2.3 times that of the surrounding area, which is consistent with values calculated from measurements made using HFTs.
, modeled heat flow from the tussock varied from 1.1 to 2.3 times that of the surrounding area, which is consistent with values calculated from measurements made using HFTs.
A rough estimate of the heat flow from an area with tussocks compared to a similar area without tussocks (but with the same snow cover) is given by

where Qt is the total heat flow from the area with tussocks, Qwt is the total heat flow from the area without tussocks, and ft is the fraction of area covered by tussocks tops. We have evaluated Equation (5) using values of tussock microrelief and areal coverage measured from contour maps (Table 1). The results indicate that the presence of tussocks can cause from 0 to a 20% increase in total heat flow depending on the value of RCALC.
Discussion
The results, which document that beneath the snow cover the depressions are warmer than the tussock tops, are not surprising. To a great extent, this effect is directly attributable to lateral differences in the thickness of the snow. In particular, when the snow cover is thin and the microrelief a large fraction of the snow depth, differences in temperature are accentuated.
More surprising, perhaps, is that the vertical heat flow from tussocks appears to be enhanced over the heat flow from adjacent areas, suggesting that there is a focusing of heal flow through the tussock. Measurements and model results indicate enhancements by a factor of 2 are possible. When multiplied by the areal coverage of tussocks at a location, the presence of tussocks could (in theory) result in a 20% increase in total heat flow from the area.
Our present model fails to incorporate some facts that may be important. First, many tussocks have height-to-width ratios near 1, in which case the assumption of one dimensional heat flow used in the model is questionable. Second, the internal structures of tussocks are complex (Reference RadforthRaup, 1965) and can consist of material that is quite different than surrounding ground. Water content can also be different. Both lead to lateral contrasts in thermal conductivity and will affect the heat flow. The snow, treated in our model as homogeneous, rarely is (Fig. 1). Instead, its thermal conductivity can vary by an order of magnitude from one layer to the next (i.e. depth hoar vs wind slab). Finally, the analysis assumes that the snow cover is the same with or without tussocks, but we have shown, in fact, that the microtopography and the development of the snow cover are closely linked, so this assumption is certainly flawed.
Still, the model gives heat flow enhancement values that are realistic (compare Figs 5 and 6), which gives us some confidence that it incorporates one important aspect of the interaction of snow and microtopography. If the results are correct, they imply that the microtopography must be considered when calculating the thermal balance. Of course, the variation in snow distribution at larger scales must also be considered (Reference Nelson, Outcalt, Hinkel, Murray, Murray and SennesetNicholson and Granberg, 1973; Reference Combarnous and BoriesDesrochers and Granberg, 1988; Reference Gold and LachenbruchGranberg, 1988) and could easily mask effects of microtopography.
Lastly, our results make it clear that measuring the temperature at the base of the snow at a single location can be highly misleading, and lead to the use of grossly incorrect values in thermal modeling. Many measurements at the interface are needed to characterize the temperature and heat flow adequately.
Conclusions
Arctic and sub-Arctic snow covers are deposited on ground with 0.1 to 0.5 m of microrelief. Since these snow covers are thin, the microrelief is a substantial portion of total snow depth and has a strong effect on the thermal regime. In situ measurements indicate that temperature variations as great as 19°C exist at the snow/ground interface over distances of less than 1 m. Measured vertical heat flow from the microtopographic highs average 1.4 to 2.1 times the heat flow from adjacent areas. A simple model suggests that the presence of microtopography can enhance overall heat flow from an area up to 20%.
Acknowledgments
We thank Daniel Solie and Carl Benson for their help collecting data during the winter of 1989–90. Bill Lee prepared the site contour maps from which we calculated the areal coverage of tussocks. Jerry Johnson helped clarify our thinking about some of the points discussed. This work was funded by U.S. Army Project 4A762784-AT42, Cold Regions Engineering and Technology.










