Longevity risk and capital markets: the 2018–19 update

This Special Issue of the Annals of Actuarial Science contains 12 contributions to the academic literature all dealing with longevity risk and capital markets. Draft versions of the papers were presented at Longevity 14: The Fourteenth International Longevity Risk and Capital Markets Solutions Conference that was held in Amsterdam on 20–21 September 2018. It was hosted by the Pensions Institute at City, University of London and the Netspar Network for Studies on Pensions, Ageing and Retirement.

Longevity risk and related capital market solutions have grown increasingly important in recent years, both in academic research and in the markets we refer to as the Life Market, that is, the capital market that trades longevity-linked assets and liabilities.¹ Mortality improvements around the world are putting more and more pressure on governments, pension funds, life insurance companies, as well as individuals, to deal with the longevity risk they face. At the same time, capital markets can, in principle, provide vehicles to hedge longevity risk effectively and transfer the risk from those unwilling or unable to manage it to those willing to invest in this risk in exchange for appropriate risk-adjusted returns or to those who have a counterpoising risk that longevity risk can hedge, for example, life offices and reinsurers with mortality risk on their books. Many new investment products have been created both by the insurance/reinsurance industry and by the capital markets. Mortality catastrophe bonds are an early example of a successful insurance-linked security. Some new innovative capital market solutions for transferring longevity risk include longevity (or survivor) bonds, longevity (or survivor) swaps and mortality (or q-) forward contracts. The aim of the International Longevity Risk and Capital Markets Solutions Conferences is to bring together academics and practitioners from all over the world to discuss and analyse these exciting new developments.

The conferences have closely followed the developments in the market. The first conference (L1) was held at Cass Business School in London in February 2005. This conference was prompted by the announcement of the Swiss Re mortality catastrophe bond in December 2003 and the European Investment Bank/BNP Paribas/PartnerRe longevity bond in November 2004.

The second conference (L2) was held in April 2006 in Chicago and hosted by the Katie School at Illinois State University.² Since L1, there have been further issues of mortality catastrophe bonds, as well as the release of the Credit Suisse Longevity Index. In the UK, new life companies backed by global investment banks and private equity firms were setting up for the express purpose of buying out the defined benefit (DB) pension liabilities of UK corporations.³ Goldman Sachs announced it was setting up such a buyout company itself (Rothesay Life) because the issue of pension liabilities was beginning to impede its mergers and acquisitions activities. It decided that the best way of dealing with pension liabilities was to remove them altogether from the balance sheets of takeover targets. So there was firm evidence that a new global market in longevity risk transference had been established. However, as with many other economic activities, not all progress follows a smooth path. The EIB/BNP/PartnerRe longevity bond did not attract sufficient investor interest and was withdrawn in late 2005. A great deal, however, was learned from this failed issue about the conditions and requirements needed to launch a successful capital market instrument.

The third conference (L3) was held in Taipei, Taiwan on 20–21 July 2007. It was hosted by National Chengchi University.⁴ It was decided to hold L3 in the Far East, not only to reflect the growing importance of Asia in the global economy but also to recognise the fact that population ageing and longevity risk are problems that affect all parts of the world and that what we need is a global approach to solving these problems.⁵ Since the Chicago conference, there had been a number of new developments, including: the release of the LifeMetrics Indices covering England & Wales, the US, Holland and Germany in March 2007 by J.P. Morgan, the Pensions Institute and Towers Watson;⁶ the world’s first publicly announced longevity swap between Swiss Re and the UK life office Friends Provident in April 2007 (although this was structured as an insurance or indemnification contract rather than a capital market transaction).

Since the Taiwan conference, there were further developments in the capital markets. In December 2007, Goldman Sachs launched a monthly index suitable for trading life settlements.⁷ The index, QxX.LS, was based on a pool of 46,290 anonymised US lives over the age of 65 years from a database of life policy sellers assessed by the medical underwriter AVS. In 2008, Institutional Life Services (ILS) and Institutional Life Administration (ILA), a life settlements trading platform and clearing house, were launched by Goldman Sachs, Genworth Financial, and National Financial Partners. ILS and ILA were designed to modernise dealing in life settlements and meet the needs of consumers by ensuring permanent anonymity of the insured and of the capital markets by providing a central clearing house for onward distribution of life settlement assets, whether individually or in structured form.⁸

Xpect Age and Cohort Indices were launched in March 2008 by Deutsche Börse. These indices cover, respectively, life expectancy at different ages and survival rates for given cohorts of lives in Germany and its regions, Holland and England & Wales.

The world’s first capital market derivative transaction, a q-forward contract⁹ between J. P. Morgan and the UK pension fund buyout company Lucida, took place in January 2008. The world’s first capital market longevity swap was executed in July 2008. Canada Life hedged £500m of its UK-based annuity book (purchased from the defunct UK life insurer Equitable Life). This was a 40-year swap customised to the insurer’s longevity exposure to 125,000 annuitants. The longevity risk was fully transferred to investors, which included hedge funds and insurance-linked securities (ILS) funds. J. P. Morgan acted as the intermediary and assumed counterparty credit risk. In August 2011, ITV, the UK’s largest commercial TV producer, completed a £1.7bn bespoke longevity swap with Credit Suisse for its £2.2bn pension plan: the cost of the swap is reported as £50m (3% of the swap value). The largest to date, covering £16bn of pension liabilities, was the longevity swap for the British Telecom Pension Scheme, arranged by the Prudential Insurance Co of America (PICA)¹⁰ in July 2014. In February 2010, Mercer launched a pension buyout index for the UK to track the cost charged by insurance companies to buy out corporate pension liabilities: at the time of launch, the cost was some 44% higher than the accounting value of the liabilities which highlighted the attraction of using cheaper alternatives, such as longevity swaps.

The fourth conference (L4) was held in Amsterdam on 25–26 September 2008. It was hosted by Netspar and the Pensions Institute.¹¹ In 2008, Credit Suisse initiated a longevity swap with Centurion Fund Managers, whereby Centurion acquired a portfolio of synthetic (i.e., simulated) life policies, based on a longevity index built by Credit Suisse. In 2009, survivor swaps began to be offered to the market based on Deutsche Börse’s Xpect Cohort Indices.

The fifth conference (L5) was held in New York on 25–26 September 2009.¹² On 1 February 2010, the Life and Longevity Markets Association (LLMA)¹³ was established in London. Its current members are Aviva, AXA, Deutsche Bank, J. P. Morgan, Morgan Stanley, Prudential (UK) PLC, and Swiss Re. LLMA was formed to promote the development of a liquid market in longevity- and mortality-related risks. This market is related to the ILS market and is also similar to other markets with trend risks, for example, the market in inflation-linked securities and derivatives. LLMA aims to support the development of consistent standards, methodologies and benchmarks to help build a liquid trading market needed to support the future demand for longevity protection by insurers and pension funds. In April 2011, the LifeMetrics indices were transferred to LLMA with the aim of establishing a global benchmark for trading longevity and mortality risk.

The sixth conference (L6) was held in Sydney on 9–10 September 2010.¹⁴ In December 2010, building on its successful mortality catastrophe bonds and taking into account the lessons learned from the EIB bond, Swiss Re launched a series of 8-year longevity-based ILS notes valued at $50m. To do this, it used a special purpose vehicle (SPV), Kortis Capital, based in the Cayman Islands. As with the mortality bonds, the longevity notes are designed to hedge Swiss Re’s own exposure to mortality and longevity risk. In particular, holders of the notes are exposed to an increase in the spread between mortality improvements in 75–85-year-old English & Welsh males and 55–65-year-old US males, indicating that Swiss Re has life insurance (mortality risk) exposure in the US and pension (longevity risk) exposure in the UK.

In January 2011, the Irish government announced that it would issue bonds that allow the creation of sovereign annuities.¹⁵ This followed a request from the Irish Association of Pension Funds and the Society of Actuaries in Ireland. If the bonds are purchased by Irish pension funds, this will have a beneficial effect on the way in which the Irish funding standard values pension liabilities. On account of a statutory deadline to submit a deficit repair plan, 2013 was a record year for bulk annuity transactions in Ireland with sovereign annuities being used in a significant number of transactions.

The world’s first longevity swap for non-pensioners (i.e., for active and deferred members of a pension plan) took place in January 2011, when J. P. Morgan executed a £70m 10-year q-forward contract with the Pall (UK) pension fund. This was a value swap designed to hedge the longevity risk in the value of Pall’s pension liabilities, rather than the longevity risk in its pension payments as in the case of cash flow swaps which have been the majority of the swaps that have so far taken place. Longevity risk prior to retirement is all valuation risk: there is no cash flow risk and most of the risk lies in the forecasts of mortality improvements. Further, the longevity exposure of deferreds is not well defined as a result of the options that plan members have, for example, lump-sum commutation options, early retirement options and the options to increase spouses’ benefits at the expense of members’ benefits.

In April 2011, the International Society of Life Settlement Professionals (ISLSP)¹⁶ formed a life settlement and derivatives committee and announced that it was developing a life settlement index. The purpose of the index is to benchmark net asset values in life settlements trading. Investors need a reliable benchmark to measure performance and the index will help turn US life insurance policies into a tradable asset class according to ISLSP. The calculation agent for the index is AA Partners.

The first pension risk transfers (PRTs) deals outside the UK took place in 2009–11. The first buy-in deal (i.e., bulk annuity purchase to hedge the longevity risk of pensions in payment) outside the UK took place in 2009 in Canada; it was arranged by Sun Life Financial and valued at C$50m. The first buy-in deal in Europe took place in December 2010 between the Dutch food manufacturer Hero and the Dutch insurer Aegon (€44m). The first buy-in deal in the US took place in May 2011 between Hickory Springs Manufacturing Company and PICA ($75m). The first buyout deal outside the UK was announced in May 2011 and involved the C$2.5bn Nortel pension plan in Canada. In September 2011, CAMRADATA Analytical Services launched a new PRT database for US pension plans. The database provides insurance company organisational information, pension buy-in and buyout product fact sheets and screening tools, pricing data, up-to-date information on each PRT provider’s financial strength and relevant industry research. Users can request pension buy-in and buyout quotes directly from providers, including American General Life Companies, MetLife, Pacific Life, Principal Financial Group, PICA, Transamerica and United of Omaha.

The first international longevity reinsurance transaction took place in June 2011 between Rothesay Life (UK) and PICA and was valued at £100m. The first life book reinsurance swap since the Global Financial Crisis took place in June 2011 between Atlanticlux and institutional investors and was valued at €60m.

The seventh conference (L7) was held at the House of Finance, Goethe University, Frankfurt, Germany on 8–9 September 2011.¹⁷

In February 2012, Deutsche Bank executed a massive €12bn index-based longevity solution for Aegon in the Netherlands. This solution was based on Dutch population data and enabled Aegon to hedge the liabilities associated with a portion of its annuity book. Because the swap is out of the money, the amount of longevity risk actually transferred is far less than that suggested by the €12bn notional amount. Nonetheless, the key driver for this transaction from Aegon’s point of view was the reduction in economic capital it achieved. Most of the longevity risk has been passed to investors in the form of private bonds and swaps.

In June 2012, General Motors Co. (GM) announced a huge deal to transfer up to $26bn of pension obligations to PICA. This is by far the largest ever longevity risk transfer deal globally. The transaction is effectively a partial pension buyout involving the purchase of a group annuity contract for GM’s salaried retirees who retired before 1 December 2011 and refused a lump-sum offer in 2012. To the extent retirees accepted a lump-sum payment in lieu of future pension payments, the longevity risk was transferred directly to the retiree.¹⁸ The deal was classified as a partial buyout rather than a buy-in because it involved the settlement of the obligation. In other words, the portion of the liabilities associated with the annuity contract will no longer be GM’s obligation. Moreover, in contrast to a buy-in, the annuity contract will not be an asset of the pension plan but instead an asset of the retirees. In October 2012, GM did a $3.6bn buyout of the pension obligations of its white-collar retirees. Also in October 2012, Verizon Communications executed a $7.5bn bulk annuity buy-in with PICA. The buyout deals in the US in 2012 amounted to $36bn.

The eighth conference (L8) was held at the University of Waterloo, Ontario, Canada on 7–8 September 2012.¹⁹

In February 2013, the first medically underwritten bulk annuity (MUBA) transaction was executed in the UK by the UK insurer Partnership.²⁰ This involved each member filling in a medical questionnaire in order to get a more accurate assessment of their life expectancy based on their medical history or lifestyle. This was particularly useful in the case of “top slicing”, where scheme trustees insure the pensioners (who will typically be the company directors) with the largest liabilities and who therefore represent a disproportionate risk concentration for the scheme. In December 2014, Partnership executed a £206m MUBA transaction with a “top slicing” arrangement for the £2bn Taylor Wimpey pension scheme. UK insurer Legal & General (L&G) transacted a £230m medically underwritten buy-in in December 2015. The process of collecting medical information has been streamlined in recent years using third-party medical data collectors, such as MorganAsh, Age Partnership and Aon’s AHEAD platform. It is expected that the share of medically underwritten derisking deals will increase significantly over the next few years in the UK, with new business more than doubling from £540m in 2014 to £1,200m in 2015.²¹ In April 2016, the two largest UK medical underwriters, Partnership and Just Retirement, merged to form the Just Group valued at £16bn.

In April 2013, L&G reported its first non-UK deal, the buyout of a €136m annuity book from New Ireland Life. In June 2013, the Canadian Wheat Board executed a C$150m pension buy-in from Sun Life of Canada, involving inflation-linked annuities, while in March 2014, an unnamed Canadian company purchased C$500m of annuities from an insurer reported to be Industrial Alliance, making it the largest ever Canadian PRT deal to date.

In August 2013, Numerix, a risk management and derivatives valuation company, introduced a new asset class called “life” on its risk modelling platform (in addition to equities, bonds and commodities). In November 2013, SPX Corp. of Charlotte, NC, purchased a buyout contract with Massachusetts Mutual Life Insurance Co as part of a deal that moved $800m in pension obligations off SPX’s balance sheet.

The ninth conference (L9) was held in Beijing, China on 6–7 September 2013.²²

In September 2013, UK consultant Barnett Waddingham launched an insurer financial strength review service which provides information on an insurer’s structure, solvency position, credit rating and key risk’s in their business model. This service was introduced in response to concerns about the financial strength of some buyout insurers.

In November 2013, Deutsche Bank introduced the Longevity Experience Option (LEO). It is structured as an out-of-the-money call option spread on 10-year forward survival rates and has a 10-year maturity. The survival rates will be based on males and females in 5-year age cohorts (between 50 and 79 years) derived from the England & Wales and Netherlands LLMA longevity indices. LEOs will be traded over-the-counter under a standard ISDA²³ contract. They allow longevity risk to be transferred between pension funds, insurance companies and investors. They are intended to provide a cheaper and more liquid alternative to bespoke longevity swaps which are generally costly and time-consuming to implement. Purchasers of the option spread, such as a pension fund, will gain if realised survival rates are higher than the forward rates, but the gains will be limited, thereby providing some comfort to the investors providing the longevity hedge. The 10-year maturity is the maximum that Deutsche Bank believes investors will tolerate in the current stage in the development of a market in longevity risk transfers. It was reported that Deutsche Bank executed its first LEO transaction with an ILS fund in January 2014.

In December 2013, Aegon executed a second longevity risk transfer to capital markets investors and reinsurers, including SCOR. Société Générale was the intermediary in the €1.4bn deal and Risk Management Solutions (RMS) was the modelling agent.

Also in December 2013, the Joint Forum reported on the results of its consultation on the longevity risk transfer market. It concluded that this market is not yet big enough to raise systemic concerns, but “their massive potential size and growing interest from investment banks to mobilise this risk make it important to ensure that these markets are safe, both on a prudential and systemic level” (Joint Forum, 2013: 2).

In February 2014, the Mercer Global Pension Buy-out Index was introduced. It shows the benchmark prices of 18 independent third-party insurers in the four countries with the greatest interest in buying out DB liabilities: UK, US, Canada and Ireland. Costs were highest in the UK where the cost of insuring £100m of pension liabilities was 123% of the accounting value of the liabilities – equivalent to £32 per £1 p.a. of pension.²⁴ The comparable costs in Ireland, the US and Canada were 117%, 108.5% and 105%, respectively. The higher cost in the UK is in part due to the greater degree of inflation uprating in the UK compared with the other countries. The difference between the US and Canada is explained by the use of different mortality tables. Rising interest rates and equity markets will lower funding deficits and hence lead to lower buyout costs in future, especially in the US.

In July 2014, Mercer and Zurich launched Streamlined Longevity Solution, a longevity swap hedge for smaller pension schemes with liabilities above £50m. This is part of a new Mercer SmartDB service which provides bespoke longevity derisking solutions and involves a panel of reinsurers led by Zurich. It reduces the costs by having standardised processes for quantifying the longevity risk in each pension scheme. The first deal, valued at £90m, was transacted with an unnamed UK pension scheme in December 2015.

The tenth conference (L10) was held at Universidad Diego Portales in Santiago, Chile on 3–4 September 2014.²⁵

In December 2014, Towers Watson launched Longevity Direct, an off-shore longevity swap hedging service that gives medium-sized pension schemes with liabilities between £1–3bn direct access to the reinsurance market, via its own cell (or captive) insurance company. This allows schemes to bypass insurers and investment banks, the traditional derisking intermediaries, and significantly reduces transactions costs and completion times, while still getting the best possible reinsurance pricing. The first reported transaction on the Longevity Direct platform was the £1.5bn longevity swap executed by the Merchant Navy Officers Pension Fund (MNOPF) in January 2015 which was insured by MNOPF IC, a newly established cell insurance company based in Guernsey, and then reinsured with Pacific Life Re. In February 2015, PwC launched a similar off-shore longevity swap service for pension schemes as small as £250m. It used a Guernsey-based incorporated cell company called Iccaria, established by Artex Risk Solutions, to pass longevity risk directly on to reinsurers. The arrangement is fully collateralised and each scheme owns a cell within Iccaria which again avoids the costs of dealing with insurer and investment bank intermediaries.

There is increasing demand from reinsurance companies for exposure to large books of pension annuity business to offset the risk in their books of life insurance. For example, in 2014, Warren Buffett’s Berkshire Hathaway agreed to a £780m quota-reinsurance deal with the Pension Insurance Corporation (PIC), a specialist UK buyout insurer.²⁶ Similarly, in August 2014, AXA France executed a €750m longevity swap with Hannover Re.

In March 2014, L&G announced the biggest single buyout in the UK to date when it took on £3bn of assets and liabilities from ICI’s pension fund, a subsidiary of AkzoNobel. In December 2014, L&G announced the largest ever UK buy-in valued at £2.5bn with US manufacturer TRW. Around £13bn of bulk annuity deals were executed in the UK in 2014, the largest volume of business since the derisking market began in 2006 and beating the previous best year of 2008, just before the Global Financial Crisis, when £7.9bn of deals were completed. The total volume of derisking deals in the UK in 2014 (covering buyouts, buy-ins and longevity swaps) was £35bn, a significant proportion of which is accounted for by the £16bn BT longevity swap.

In November 2014, the Longevity Basis Risk Working Group (2014) of the Institute and Faculty of Actuaries (IFoA) and LLMA published “Longevity Basis Risk: A Methodology for Assessing Basis Risk”. This study develops a new framework for insurers and pension schemes to assess longevity basis risk. This, in turn, will enable simpler, more standardised and easier to execute index-based longevity swaps to be implemented. Index-based longevity swaps allow insurers and pension schemes to offset the systematic risk of increased liabilities resulting from members living longer than expected. It had hitherto been difficult to assess how effectively an index-based longevity swap could reduce the longevity risk in a particular insurance book or pension scheme. The methodology developed in the report is applicable to both large schemes (which are able to use their own data in their models) and smaller schemes (by capturing demographic differences such as socio-economic class and deprivation).

In March 2015, the UK government announced that it would introduce a new competitive corporate tax structure to allow ILS to be domiciled in the UK and the associated Risk Transformation Regulations 2017, creating a new regulated activity of insurance risk transformation, came into effect in December 2017. In May 2015, Rothesay Life, the insurance company owned by Goldman Sachs, bought out the liabilities of Lehman Brothers’ UK pension scheme for £675m, thereby securing the pensions of former employees of the company associated with the beginning of the Global Financial Crisis. In April 2016, Rothesay bought two-thirds of Aegon’s UK annuity book – representing 187,000 policy holders – for £6bn, bringing total assets under management to £20bn and total lives assured to over 400,000. This was the first substantial annuity transfer since the introduction of Solvency II in January 2016. This new solvency regime for EU-based insurers increased capital requirements and has reduced the attractiveness of annuities as a business line for certain insurers and raised buyout prices by 5–7%.²⁷

In 2015, L&G entered both the US and European PRT markets. It executed a $450m transaction with the US subsidiary of Royal Philips covering 7,000 scheme members in October and a €200m deal with ASR Nederland NV, a Dutch insurer in December. The pension obligations were transferred to L&G Re in cooperation with Hannover Re. L&G said: “The pension risk transfer market has become a global business…The potential market for pension risk transfer in the US, UK and Europe is huge, and will play out over many decades”. Two US insurers were also involved in the Royal Philips deal: PICA also acquired $450m of scheme liabilities covering another 7,000 members, while American United Life Insurance Company issued annuity contracts to 3,000 deferred scheme members, valued at $200m.

In January 2015, the Bell Canada Pension Plan executed a C$5bn longevity swap with Sun Life Financial,²⁸ SCOR, and RGA Re; it was SCOR’s first transaction in North America. In the process, Canada became the first country apart from the UK to have all three PRT solutions actively in use. In the same year, it completed its first inflation-linked buy-in annuity transaction, while in 2017, it completed its first buy-in annuity covering active future benefits.²⁹ In June 2015, Delta Lloyd did a second €12bn longevity swap with RGA Re: the swap was also index-based, with an 8-year duration and had a notional value of €350m.³⁰ In July 2015, Aegon executed one valued at €6bn with Canada Life Re, a new entrant to the derisking market in 2015. Another new entrant was Scottish Widows.

In June 2015, the Mercer Pension Risk Exchange was launched. It gives clients in the US, UK and Canada up-to-date buy-in and buyout pricing based on their plan’s data. It collects prices provided monthly by insurers in the bulk market, based on plan benefit structures and member data. Mercer said: “Many companies have the appetite to transfer pension risk off their balance sheet, but they face barriers: lack of clear information about the true cost of a buy-in or buyout, limited transparency, the fluctuation of market rates and plan economics to name but a few. [The exchange will enable] sponsoring employers and trustees to be more strategic and sophisticated in their approach and to know that they are executing a buy-in or a buyout at the best time for them and at a competitive price”.

The eleventh conference (L11) was hosted by Université Lyon 1, Lyon, France on 7–8 September 2015.³¹

In April 2016, Willis Towers Watson (WTW) released PulseModel which uses medical science and the opinions of medical experts to improve longevity predictions. For example, the model predicts that 16% of 50-year-old men in the UK will develop type 2 diabetes in the next 20 years, but this rises to 50% for those who are both obese and heavy smokers. Overall, the model predicts that longevity improvements in the future will be lower than currently predicted, at around 1% p.a. rather than 1.5%. If this turned out to be correct, then the current price of longevity of risk transfer products would be too high.

The largest buy-in in 2016 (in December) was Phoenix Life’s £1.2bn buy-in for the 4,400 pensioners in the PGL Pension Scheme, which is sponsored by the Phoenix Group, Phoenix Life’s parent company. This replaced a longevity swap that it had set up for the plan in 2014. This is the first example of a transaction which transforms a longevity swap into a bulk annuity. Phoenix Life saw this as an opportunity to bring £1.2bn of liquid assets (mostly UK government bonds) onto its balance sheet, which could then be swapped into a higher yielding, matching portfolio, structured to maximise the capital benefit under Solvency II. This, in turn, meant that Phoenix Life would be assuming the market risks associated with the PGL scheme pension liabilities in addition to the longevity risks – and already does this on its existing book of individual annuities which are backed by £12bn of assets. The timing was also critical. Phoenix wanted to ensure that its internal model under Solvency II had bedded down well and that the capital and balance sheet impacts of the transaction were well understood, and that Phoenix had elicited the full support of the UK Prudential Regulation Authority (PRA)³² for the transaction, thereby ensuring execution certainty. Phoenix also provided comfort to the plan’s trustees by giving them “all-risks” cover from point of buy-in (“all-risks” cover is not usually provided until buyout) and strong collateral protection.³³

The year 2016 saw the beginning of a trend towards consolidation among insurance companies involved in the longevity risk transfer business in the UK. For example, Aegon sold its £9bn UK annuity portfolio to Rothesay Life and L&G between April and May, as part of a strategy to free up capital from non-core businesses. Part of the reason for this is the additional capital requirements under Solvency II. Similarly, in September, Deutsche Bank sold its Abbey Life subsidiary to Phoenix Life – a consolidator of closed insurance books – for £935m, as part of a planned programme of disposals aimed at restoring its capital base. There is an estimated £100bn of UK individual annuities in back-books and further consolidation of these back-books is anticipated. In December 2017, L&G sold its £33bn closed book of traditional insurance-based pensions, savings and investment policies to the ReAssure division of Swiss Re for £650m.

Solvency II has also been blamed for some companies pulling out of the bulk annuities market altogether, a key example being Prudential (UK) in January 2016. Prudential (UK) announced it would be selling a portion of its £45bn UK annuity and pension liability businesses due to an inadequate return on capital and to transfer that capital to its growing businesses in Asia.³⁴ Reinsurance deals have also increased in response to Solvency II, involving non-EU reinsurers. For example, PIC executed a £1.6bn longevity reinsurance agreement with PICA in June 2016.

The year 2016 also witnessed the increasing streamlining and standardisation of contracts. This is particularly beneficial to small plans below £100m. Previously, smaller plans have been less attractive to insurers due to the higher costs of arranging such deals relative to the profit earned. To circumvent this, consultants have begun offering services that allow smaller plans to access improved pricing and better commercial terms using a standardised off-the-shelf process incorporating pre-negotiated legal contracts. Pricing is more competitive because the insurer’s costs are kept low. An example is WTW’s Streamlined Bulk Annuity Service. The increasing maturity of the market has meant that some larger plans have also been prepared to use pre-negotiated contracts.

The year 2016 was also the tenth anniversary of the longevity transfer market. Since its beginning in the UK in 2006, £40bn of buyouts and £31bn of buy-ins have taken place in the UK, covering 1 million people.³⁵ Yet this equates to just 5% of the £1.5trn of UK DB pension assets and 3% of the £2.7trn of DB pension liabilities on a buyout basis. In addition, 48 longevity swaps are known to have been completed in the UK between 2007 and 2016, valued at £75bn and covering 13 insurance companies’ annuity and buyout books, 22 private sector pension funds and one local authority pension fund (some of which executed more than one swap).³⁶ Figure 1 shows the growth of the global market in longevity risk transfer between 2007 and 2018. A total of $434bn in transactions have been completed during this period.

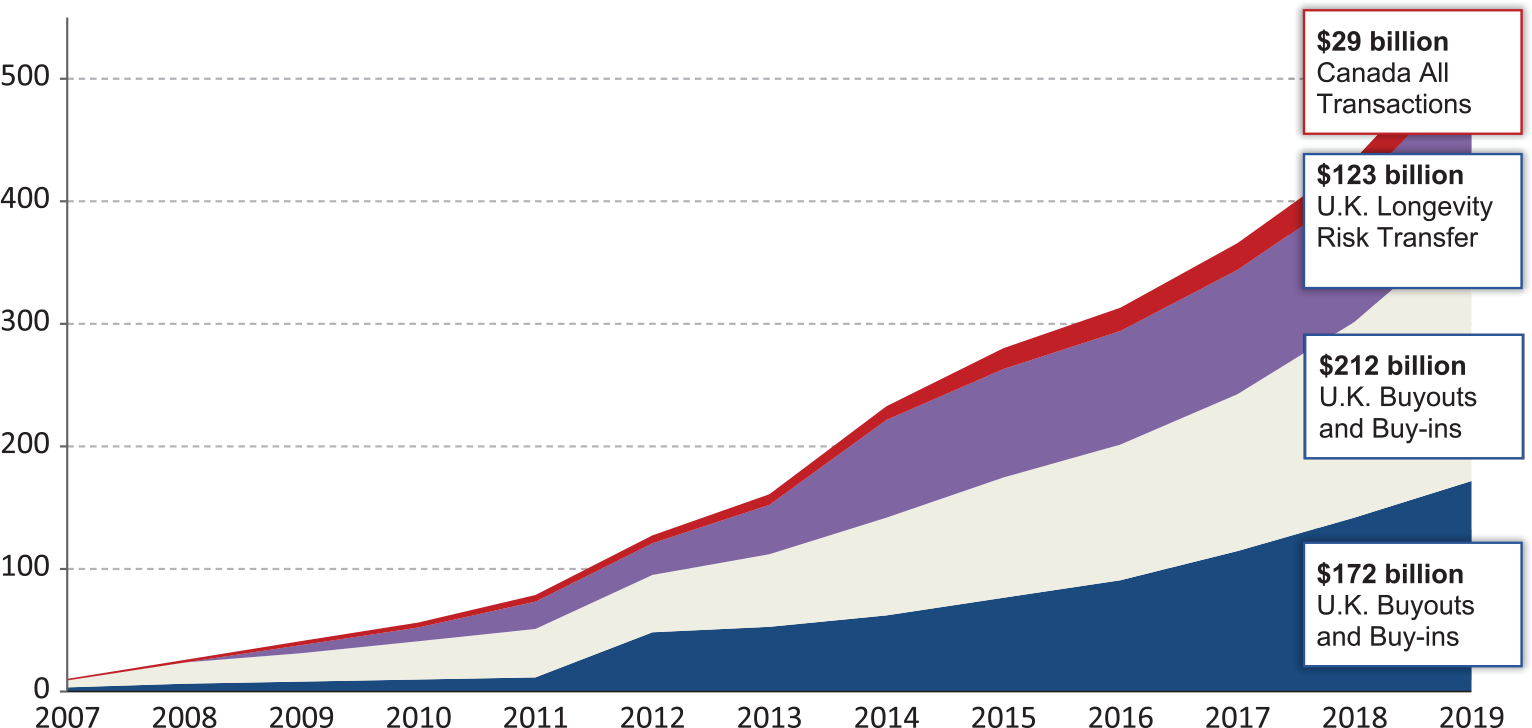
Figure 1 Cumulative pension risk transfers by product and country, $bn, 2007–2019.

The twelfth conference (L12) was held in Chicago on 29–30 September 2016 and hosted by the Society of Actuaries and the Pensions Institute.³⁷

At the beginning of 2017, there were eight UK-domiciled insurers actively participating in the PRT market in the UK. The largest players are PIC and L&G, with market shares of 37% and 30%, respectively. The others are Rothesay Life, Canada Life, Zurich, Scottish Widows, Standard Life and new entrant Phoenix (since August). Occasionally, the insurers cooperate in a transaction. To illustrate, in August 2017, L&G executed a longevity swap in respect of £800m of the pension liabilities of Scottish and Southern Energy (SSE), while PIC completed a £350m buy-in for the company. Consultant LCP estimated that £12bn buy-ins and buyouts took place in 2017 and £19bn took place in 2018, with total insurer capacity at £25bn: “There remains significant capacity and competition – even if a large back-book comes to market – providing attractive opportunities for pension plans to transfer longevity risk through a buy-in or buy-out”.³⁸

One of the largest deals in 2017 (in September) involved a £3.4bn longevity swap between the Marsh & McLennan Companies (MMC) UK Pension Fund and both Canada Life Reinsurance and PICA, using Guernsey-based incorporated cell companies, Fission Alpha IC Limited and Fission Beta IC Limited. MMC subsidiary Mercer led the transaction as adviser to the pension fund trustee and the deal was the first to be completed using the Mercer Marsh longevity captive solution, with no upfront premium. The two reinsurers shared the risk equally and the use of the captive ICC vehicle meant that no insurer intermediary was required, making the deal more cost-effective for the pension fund.³⁹ Also in September, the British Airways’ Airways Pension Scheme used a similar Guernsey-based captive insurer to set up a £1.7bn longevity swap. The longevity risk was then reinsured with Partner Re and Canada Life Re. The scheme had previously hedged £2.6bn of liabilities through two longevity swap transactions executed by Rothesay Life in 2010 and 2011.⁴⁰ In November 2017, PIC executed a £900m longevity swap with PICA, while in December 2017, L&G executed a £600m longevity swap with PICA.⁴¹

In December 2017, NN Life, part of the Nationale-Nederlanden Group, executed an index-based longevity hedge with reinsurer Hannover Re, in a deal covering the insurer against the longevity trend risk in €3bn of its liabilities. The structure is similar to the 2013 Aegon tail-risk deal arranged by Société Générale and builds on subsequent work including Michaelson and Mulholland (2015) and Cairns and El Boukfaoui (2018). While the term of the transaction is 20 years, NN Life is protected over a longer time period via a commutation function⁴² that applies at maturity. If longevity improvements have been much stronger than expected, this will be assumed to continue until the liabilities run-off and NN will receive a payment under the hedge. The transaction helped to reduce the solvency capital requirement of NN’s Netherlands life business by €35m. The index attachment point for the hedge is close to NN’s best estimate, which helps maintain the Solvency Capital Requirement (SCR) relief and effective risk transfer over time.^{43, 44}

In order to reduce the costs of derisking, pension plans are encouraged to perform some liability reduction exercises, the key ones being:⁴⁵

• Enhanced transfer values (ETVs) – allow deferred members to transfer an uplifted value of their benefits to an alternative arrangement. In August 2017, a 64-year-old entitled to an index-linked pension starting at £10,000 from the age of 65 years would be offered a transfer value of £237,000, according to the Xafinity Transfer Value Index.⁴⁶ In October 2019, the transfer value was £244,200. In 2019, around 50,000 members transferred out of their DB scheme, around 1% of eligible members.⁴⁷

• Flexible retirement options (FROs) – allow deferred members aged 55 years and over to retire early, or to take a transfer value and secure benefits in a different format from their plan benefits, or to use funds for drawdown purposes.

• Pension increase exchanges (PIEs) – allow pensioners to exchange non-statutory increases for a higher immediate pension with lower or even zero future increases (e.g. a £10,000 annual pension with inflation uplifting is replaced by a £12,000 annual pension with no further increases).

• Trivial commutations (TCs) – allow members with low value benefits to cash these in.

The most common exercises currently in the UK are PIEs and TCs – and these can be conducted either before or at the same time as a bulk purchase annuity (BPA) broking exercise.

Innovation is a continuing feature of this market. Some examples include (see, e.g. Legal & General and Engaged Investor, 2016):⁴⁸

• Buy-ins and buyouts with deferred premium payments – to spread costs, schemes that cannot afford the upfront premium of a derisking solution pay for it in instalments over a number of years.

• Buyouts combined with a longevity hedge.⁴⁹

• Phased buy-ins, where the largest risks or the lowest cost risks are insured first.

• Phased derisking using a sequence of partial buy-ins with an “umbrella” structure to avoid more than one set of contract negotiations – to spread costs.

• Accelerated buy-ins – the insurer provides a loan to the plan equal to the deficit (sometimes called a winding-up lump sum (WULS)), so that a partial buy-in can take place immediately, with this converting to a full buy-in when the loan has been repaid, or with the option of a full buyout at a later date.

• Forward start buy-ins – a standard buy-in with the start date delayed to reflect the level of funding available, with additional options, such as paying deferred members as and when they retire if this is prior to the start date, or the ability to bring forward the start date for an additional fee.

• Self-managed buy-ins – which allows pension schemes to run their own asset management strategy at lower cost and with a lighter regulatory burden than if an insurer was involved (introduced in 2018 by the UK asset manager Insight Investment). The strategy uses swaps to hedge interest, inflation and longevity risks and is estimated to be 10–15% cheaper than the equivalent insurance product.⁵⁰

• Automated bulk plan transfers – to reduce risks (introduced in November 2017 by Scottish Widows and Standard Life).⁵¹

• Top-slice buy-ins – to target the highest value liabilities.

• Named-life longevity swap – if the named member lives longer than expected, the insurer pays out the difference (examples being the £400m Bentley plan or an unnamed plan with 90 named pensioners valued at £50m).

• Tranching by age – to reduce costs; according to consultant Punter Southall, a buy-in for pensioners up to the age of 70 years will make a subsequent buyout within the following 10 years cheaper than a buy-in for the over 70s.⁵²

• Longevity swaps for small pension plans with liabilities of £50–100m – previously only available for medium (£100–500m) and large plans (above £500m).

• Novation – the ability to transfer a longevity hedge from one provider to another, thereby introducing some liquidity into what had previously been a completely illiquid market. An example would be the reinsurance of a small bulk annuity transaction. Contract simplicity is a desirable feature of such arrangements.

• Longevity swap to buy-in conversions – as pioneered by Phoenix Life in December 2016 for its parent company’s pension plan. Solvency II incentivises buy-in providers to hold longevity insurance, otherwise they pay an additional risk margin. This encourages buy-in providers to seek out plans which already have a longevity hedge and encourage them to do a buy-in. Another driver is longevity swap providers that are not currently active in the market – such as J.P. Morgan and Credit Suisse – but are still responsible for running off their existing swaps. They might have an incentive to encourage the associated pension plan to novate the swap to a buy-in provider and hence extinguish their liability.⁵³

• Insuring away the extreme tail of liabilities in a closed plan after a specified term, such as 5 or 10 years – to reduce costs.

• Increasing optionality in contracts to improve flexibility – for example, the option to switch the indexation measure for pensions in payment from the Retail Price Index to the Consumer Price Index if government legislation changes; or the option to secure discretionary benefits, such as actual inflation above a 5% cap; or surrender options.

• Insuring the tail of the liabilities – whereby a closed scheme that cannot afford a full buyout insures only the liabilities after a certain point in time, say, 10 years’ ahead.

• Combining liability management solutions (such as interest rate and inflation swaps, and ETV, FRO and PIE exercises) and bulk annuities in a buyout – so instead of completing liability management before considering a buyout, plans do this in a single exercise.

• “Buy-out aware” investment portfolios – used to reduce buyout price volatility and close the funding shortfall, with the buyout price locked to the value of the buyout aware funds once a target shortfall has been reached and while the contract documentation for a buyout is being completed.

• Improved arrangements for handling data errors that arise after a deal has been executed – to reduce pre-deal negotiation requirements and post-deal transaction uncertainty. Common data errors include member gender, date of birth, and benefit amounts for both member and partner. A simplified data error process could deal with these issues in the following way: locking down benefits, removing the need for re-pricing; mechanistically adjusting demographic errors; and using due diligence to check for systematic errors with the data.⁵⁴

• Residual risk insurance, covering, for example, benefit specification errors, data errors and unidentified beneficiary cover.

• Arrangements to handle deferred members – to improve insurer appetite to assume the additional risk and cost involved. Deferred lives make up almost half (45%) of the membership of UK DB plans in the UK.⁵⁵ They are much more expensive to hedge for a number of reasons. First, there can be problems with their existence and identification. Second, they enjoy a large number of options which need to be priced.⁵⁶ Third, their longevity risk is greater, because the longevity improvement assumption used for pricing has greater reliance on the assumed long-run trend.⁵⁷ Fourth, as a direct consequence of the previous points, more capital is needed and this, in turn, increases the demand for reinsurance. These issues can be at least partially mitigated as follows: a robust existence checking procedure is needed involving electronic tracing, assuming a fixed percentage of the pension is exchanged for tax-free cash, setting the assumed retirement date to the plan’s normal retirement date, assuming no pension is exchanged for additional partner pension, restricting the age profile to older deferred members and restricting the proportion of deferred members in the transaction.⁵⁸

These are all innovations in the space linking pension plans and insurance companies designed to ease the transfer of pension liabilities (or at least the longevity risk in them) from pension plans to insurance companies.

The innovations have helped to encourage more business, but this is, in turn, has exposed potential longer-term capacity constraints within insurance companies. As one consultant said: “Given the market has historically completed only 150–200 deals in any one year, there is a real risk of capacity constraints in the market, not just from an insurer capital perspective, but also from a resource and expertise perspective”.⁵⁹

A total of £12.4bn in buy-ins and buyouts and £.6.4bn in longevity swaps took place in the UK in 2017.

In April 2015, the UK government introduced “Freedom and Choice” pension reforms which gave more flexibility to how individuals could draw down their defined contribution (DC) pension pots.⁶⁰ In particular, there was no longer a requirement to purchase an annuity.⁶¹ This immediately led to a fall in annuity sales by around 75% (Cannon et al., 2016). The situation was not helped by the fall in gilt yields (which led to a corresponding fall in annuity rates) arising from the government’s quantitative easing programme introduced after the Global Financial Crisis. In August 2017, a 65-year-old with a £100,000 pension pot could get a level income for life of £4,894: two years before, the amount would have been £5,292.⁶² By 2017, the following insurers had pulled out of the open market for annuities: Aegon, LV=, Partnership (before it merged with Just Retirement to form Just Group), Prudential (UK), Standard Life, Friends Life (merged with Aviva), Reliance Mutual, B&CE and Retirement Advantage. This leaves just six providers left in what was once the world’s largest annuity market: Aviva (offering standard and enhanced annuities), Canada Life (standard and enhanced), Hodge Lifetime (standard only), Just Group (enhanced only), L&G (standard and enhanced) and Scottish Widows (standard and enhanced).⁶³

In place of annuities, individuals took their pension pot either as a lump sum or they purchased an income drawdown product. In both cases, they bear their own longevity risk. Evidence shows that people systematically underestimate their life expectancy which implies that there is a significant probability that many people will spend their pension pot before they die. A recent study by Just Group found that UK men aged 40–54 years expect to live until 78.9 years on average, whereas official estimates of their life expectancy is 87.5; the figures for women are 80.5 and 90.1.⁶⁴

A number of UK insurers providing bulk annuities for buy-ins are also involved in the UK equity release mortgage (ERM, or reverse mortgage or lifetime mortgage) market which allows home owners to borrow against the equity in their homes. The modern form of the market began when the Equity Release Council representing providers was established in 1991 with a voluntary code of conduct that offered a number of guarantees. Before this, users of the product could lose their homes when the value of the loan plus interest exceeded the value of the property. Since 1991, there is a guaranteed right to remain living in the property, either for life or until entry into long-term care. In addition, there is a No Negative Equity Guarantee (NNEG) which means that the value of the loan plus interest can never exceed the value of the property, and so no debt can be passed on to the estate of the equity release borrower. The providers in the new market therefore face longevity risk in a way that those in the old market did not. In 2017, a total of £3bn in equity release loans were made with an average size loan of £102,000. In 2018, the UK Prudential Regulation Authority (2018) raised concerns that providers were not properly reflecting the cost of the NNEG in their capital reserving. Instead of valuing the NNEG using the Black (1976) model as a series of put options on the forward house price (which is lower than the current price to reflect the loss of rent due to deferred possession) weighted by the probability of mortality, morbidity and pre-payment, it pointed out that most providers were using the expected future price which required assumptions about property growth.

There were also important developments outside the UK in 2017, although many of these involve innovations adopted from the UK market. Apart from the US, Canada and the Netherlands, new markets include Germany, Switzerland and Ireland. Examples of innovations in the US include: plan-specific mortality data – with $250m as the minimum transaction size; asset-in-kind premium funding – where bonds are used to fund the transaction. Insurer capacity has also increased, with 14 insurers engaged in pension buyouts. Three new insurers joined: Athene,⁶⁵ Mutual of America and CUNA Mutual. Athene wrote more than $2bn of business in 2017. A total of $24.7bn PRTs were conducted in the US in 2017. In Canada, group annuity sales amounted to C$3.7bn, and a new group annuity provider, Brookfield Annuity, joined the market. In Germany, many schemes are considering using lump-sum settlement payments to pensioners to transfer longevity risk. In Switzerland, insurers are now willing to consider transfers involving active members. In Ireland, Danske Bank transferred €335m of its Irish DB pension liabilities to Irish Life.⁶⁶

In April 2017, the International Monetary Fund (IMF) released a new edition of its Global Financial Stability Report. Chapter 2 (“Low Growth, Low Interest Rates, And Financial Intermediation”) suggests that DB pension funds across the globe might have to cut benefits “significantly” in the long term because of ultra-low interest rates. Attempts to increase returns by changing asset allocations “appears feasible only by taking potentially unacceptable levels of risk”. In the face of such low rates, the IMF argues that “life insurers and pension funds would face a long-lasting transitional challenge to profitability and solvency, which is likely to require additional capital” or would require a “very high” level of volatility risk to meet their funding goals. However, a combination of risk aversion and regulatory constraints was likely to deter the vast majority from taking this second path. The IMF instead believes that the current situation might work to the benefit of insurers backing buy-ins and buyouts. With investors increasingly monitoring the size of DB liabilities and the effects on company share prices, profits and dividends, the IMF said offloading these liabilities to insurers “is an attractive option” and “may represent a market-efficient arrangement” and that “regulation could play an important role in this area by facilitating such transactions”.

The thirteenth conference (L13) was held in Taipei, Taiwan on 21–22 September 2017. It was hosted by the Department of Risk Management and Insurance and the Risk and Insurance Research Center at National Chengchi University, and by the Pensions Institute at Cass Business School.⁶⁷

2018 saw the start of a trend towards consolidation among pension schemes in the UK. This was led by a group of private equity investors. One example is the Pension Superfund which was launched in March with capital provided by Disruptive Capital and Warburg Pincus. It promises employers a cheaper way to offload their pension obligations than a traditional insurance buyout. Any surplus of assets above 115% of liabilities “on a prudent actuarial basis” will be shared one-third to members and two-thirds to the investors. The liabilities would be hedged and the investment strategy would be “fairly low risk”. The Pension Superfund would be initially targeting schemes with assets between £200m-£1bn with a strong sponsor covenant. Another example is Clara. Insurers have expressed concerns that since such pension consolidation vehicles come under the Pensions Regulator (i.e. are classified as pension schemes), they do not have to satisfy the much stricter solvency requirements of insurers which are regulated by the PRA, which is part of the Bank of England.⁶⁸ As of the end of 2019, no deals involving either the Pension Superfund or Clara had been completed, since both organisations were still awaiting regulatory approval and the government was still considering an authorisation, supervision and solvency regime.⁶⁹

The General Data Protection Regulation (GDPR) was introduced in all EU member states in May 2018 and will affect longevity risk transfers since they involve the exchange of personal data. There are fines for data protection breaches. The GDPR distinguishes between data controllers – people who determine how and why data should be used – and data processors – who process data on behalf of data controllers. Pension scheme trustees will be data controllers, as will insurers if they have received personal data in connection with a potential buyout transaction (e.g. if they are conducting a data cleansing or medical underwriting exercise). In other cases, insurers might be classified as data processors. International data transfers, for example, in the case where an insurer wants to transfer data to a reinsurer located outside the European Economic Area, can only take place if adequate data protections are in place. Care needs to be taken even if anonymised data are transferred, since it might still be possible to identify the individuals to whom the data relate, for example, company directors might be identified from information about the size of their pension benefits and date of birth.

2018 longevity risk transfer highlights for the UK included:⁷⁰

• PIC reinsured all its pensioner liabilities (73% of its total exposure) with Partner Re in January. It also helped to fund University Partnerships Programme acquisitions of student accommodation with index-linked bonds in February.

• Scottish Widows executed a £1.3bn longevity swap with PICA in February.⁷¹ It was the last UK insurer to hedge at least some of its longevity risk. It did this to reduce its Solvency II capital requirements.

• Standard Life Aberdeen sold £2.93bn of its annuity back-book to Phoenix in February, with the rest of Standard Life Assurance sold to Phoenix in September.

• Prudential (UK) sold £12bn of its annuity back-book covering 400,000 policies to Rothesay Life in March, making Rothesay the UK’s largest specialist annuity insurer with more than £37bn of assets and 750,000 lives insured.⁷²

• In March, Marks & Spencer Pension Scheme executed two buy-ins totalling £1.4bn with Aviva and Phoenix covering 15% of its pension liabilities. It was Aviva’s largest buy-in to date (at £925m) and Phoenix’s first external buy-in (at £475m).

• In March, PIC and PICA introduced a “flow reinsurance” system which automates the longevity reinsurance element of buyouts and buy-ins for schemes with liabilities below £200m. The system allows PIC to secure a commitment from PICA to assume the longevity risk early on in a transaction.

• In March, employee benefits consultant, JLT, launched a “buy-out comparison service” and monitoring tool which allows schemes to upload their own data and receive regular bulk annuity quotations from eight insurers currently active in the market.

• In April, JLT became the first consultant to implement Club Vita’s longevity analytics capabilities which have been incorporated into RiskFirst’s PFaroe modelling system for DB plans. This will allow JLT clients to set best-estimate longevity assumptions.⁷³ Club Vita data shows that pension schemes can have a very different demographic composition compared with the national population, with liabilities that could be up to 10% higher or lower as a result of different mortality experience.

• PIC executed a £900m longevity swap with PICA in May, covering 7,500 pensioners.⁷⁴

• In June, Canada Life sold its £2.7bn back-book of 155,000 UK life and pension savings policies to Scottish Friendly. The company said it wanted to concentrate on developing new retirement products following its acquisition of Retirement Advantage, an annuity and retirement income specialist, in January.

• Siemans completed a £1.3bn buy-in of its UK pension liabilities covering 6,000 members with PIC in July.

• Aviva executed a £1bn longevity swap with PICA in August.

• National Grid Electricity Group completed a £2bn longevity swap with Zurich⁷⁵ for the Electricity Supply Pension Scheme also in August.

• In August, L&G entered the small scheme longevity insurance market after completing a £300m longevity swap with an unnamed pension fund. The deal had a “streamlined structure” with simplified data requirements which helped to keep fixed costs down. The swap was later reinsured with SCOR. According to L&G, “the transaction demonstrates that longevity reinsurance is a realistic option for most pension schemes, including for trustees whose schemes are not quite at the point they can enter into buy-in or buyout, but want to manage their longevity risk”.

• In September, the British Airways’ Pension Scheme entered into the UK’s largest buy-in agreement to date (at £4.4bn) with Legal & General, covering 60% of pensioner liabilities; taking account of the £1.7bn longevity swap agreed in 2017, the scheme has now hedged 90% of its longevity risk.

• The Automobile Association Pension Scheme completed a £351m buy-in with Canada Life also in September.

• In October, the UK pension scheme of Nortel, the Canadian telecoms company which became insolvent in 2009, agreed a £2.4bn buyout deal with Legal & General, covering 15,000 pensioners and 7,200 deferred members, thereby avoiding entering the UK Pension Protection Fund which takes on the assets and liabilities of failed companies.

• In December, PIC executed another longevity swap, this time with SCOR, covering 8,000 pensioners and valued at £1.2bn.⁷⁶

In April 2018, the PRA said it was concerned that too much longevity risk was being transferred offshore through reinsurance arrangements, preferring that more of it be retained in the UK. It said it would consider amending Solvency II risk charges to encourage greater retention. While it said it understood the need for risk transfer, it said that it was concerned that pension assets were being transferred overseas, taking them outside of its regulation, so that if an offshore reinsurance firm failed, UK pensioners might not get their pensions.⁷⁷

Around £42bn longevity risk transfer deals were announced for the UK in 2019.⁷⁸ XPS reported that for a medium-sized scheme, pensioner member transfers used a “gilts + 0.3% pa” discount rate to value the liabilities, while for deferred members the discount rate was “gilts – 0.5% pa”.⁷⁹ Highlights included:

• In January, PIC invested £125m in Exeter University accommodation in order to generate index cash flows to pay its pensioners.

• In the same month, PIC completed a £425m buy-in with the Co-operative Group’s Somerfield Pension Scheme.

• L&G executed buy-ins with the Pearson Pension Plan (£500m in February), Howden Group Pension Plan (£230m in March) and 3i Group (£95m in April).

• Rothesay completed a buy-in (amount undisclosed) with the Teachers Assurance Group Pension Scheme in February, and a £110m buyout with the Laird Pension Scheme in April.

• Also in April, PIC completed a £1.2bn buy-in with Commerzbank in respect of the Dresdner Kleinwort Pension Plan of its UK subsidiary.

• In May, PIC and Phoenix insured £900m and £460m, respectively, of the liabilities of Marks & Spencer’s UK pension scheme.

• In June, Rolls Royce executed the biggest buyout to date – at £4.6bn – with L&G, covering the benefits of 33,000 pensioners. As part of the deal, a longevity swap originally with Deutsche Bank was transferred to L&G – the first time a swap has been novated between counterparties.

• In July, Scottish Widows completed buy-ins totalling £830m with Peugeot and QinetiQ

• In August, PIC executed a £3.4bn derisking deal with the British American Tobacco UK Pension Fund covering both 8,300 pensioners and 2,300 deferred members. It is the biggest deal to date covering both retired and non-retired members.

• In August, PICA completed a £7bn longevity swap with banking group HSBC’s UK pension scheme – making it the second largest swap in the UK after the £16bn swap for the British Telecom Pension Scheme in 2014, also arranged by PICA. The transaction – which covers half of the scheme’s pensioner liabilities – was structured as an insurance contract with a Bermuda-based, HSBC-owned captive insurer, which reinsured the longevity risk with PICA. It was the first captive longevity reinsurance transaction for a pension scheme associated with a major bank. Amy Kessler, PICA’s head of longevity risk transfer, said “The captive approach has become the strategy of choice for large pension schemes seeking to hedge longevity risk”.⁸⁰

• In August, Phoenix Life completed a £1.1bn buy-in of its own DB pension scheme, the PGL Pension Scheme.

• In August, Rothesay Life executed a £520m buy-in with the Cadbury Mondelēz Pension Fund, covering 1,900 pensioner members.

• In August, L&G announced it had completed a buy-in transaction for the UK hybrid pension scheme of data and technology company Hitachi Vantara. The deal was described as “innovative” since it also took into account the DC elements of the scheme. Each member’s retirement benefit is based on the higher of the DB and DC pension over their career with Hitachi Vantara. The buy-in was structured to maintain this arrangement, allowing deferred members to “consider their options” prior to a full buyout.⁸¹

• In September, L&G arranged a £930m buy-in with the Tate & Lyle Pension Scheme, covering 4,800 members.

• In September, Rothesay Life executed an even larger buy-in than the Rolls Royce deal – at £4.7bn – with the GEC 1972 Plan, covering 39,000 members split 70–30 pensioners and deferreds. There is an option for a buyout at a later date. Hence, this is known as a “buy-in to buy-out deal”. The parent company of GEC is Telent.

• Also in September, Rothesay Life insured £3.8bn of members’ benefits for the Allied Domecq Pension Fund in another buy-in covering around 27,000 pensioners and deferred members, spilt 63–37. The parent company of Allied Domecq is the Pernod Ricard Group.

• In October, Rothesay completed a £2.8bn buy-in with the National Grid Pension Scheme (Section A). The following month, L&G completed a £1.6bn buy-in with the National Grid Pension Scheme (Section B), covering 6,000 pensioner members.

• In October, Rothesay executed a full buy-in with retailer ASDA (owned by Walmart) for £3.8bn, covering 4,800 pensioners and 7,500 deferred members. This will convert to a full buyout in 2020 or 2021 at an additional cost of £800m.

• In October, Aviva Life and Pensions UK completed a £1.7bn buy-in for the Aviva Staff Pension Scheme, covering 1,500 pensioners and 4,300 deferred members.

• In November, Phoenix completed a £144m buy-in with the Aegon UK Staff Retirement and Death Benefit Scheme.

• In December, Zurich and Hannover Re completed a £800m longevity swap with an unnamed FTSE100 company.

Other UK developments in 2019 included:

• In February, L&G launched Track My Apps, a tracking service provided by fintech company Origo, to enable advisers track their clients pension transfers online.

• £936m of equity release deals in the first quarter with 20,000 households, taking out an average of £50,000 in housing wealth.

• In May, L&G announced the creation of a UK retirement housing business called Guild Living which plans to deliver 3,000 new homes over the next 5 years with a gross development value of £2bn.⁸² The business will contribute the income it needs to pay the benefits on its longevity risk transfer business. In August, L&G announced it had acquired a site in Walton-on-Thames suitable for building 300 homes.

• In June, L&G launched the first PRT execution platform to be driven by blockchain technology. Known as “Estua-Re”, the technology provides a “single ecosystem capable of driving every stage of the PRT reinsurance value chain”, including pricing, claims handling, financial reporting and collateral. It allows multiple parties to transact with each other without the need for an intermediary and there will be greater transparency since all parties will have access to the latest version of the ledger database.⁸³

• In August, PICA and the Phoenix Group launched a reinsurance counterparty to provide longevity reinsurance for insurers in the UK PRT market, covering both their buyout and buy-in transactions. Phoenix head of bulk annuities Justin Grainger said “Phoenix views longevity reinsurance as a key risk management tool. This transaction brings further depth to our reinsurer relationships and enhances our ability to offer competitive terms to pension schemes as we continue to develop our de-risking proposition”. Prudential Financial head of international transactions for longevity risk transfer Rohit Mathur said: “[PICA] has consistently focused on supporting the entire UK pension de-risking market. The addition of Phoenix is a culmination of our efforts over the past several years to do just that. We have invested in our pricing and transaction teams and …and we are happy to be in a position to support the robust pipeline of pension buy-ins and buyouts seeking to be completed while market conditions hold”. PICA was advised in this deal by Willkie Farr & Gallagher, while Phoenix was advised by CMS and Eversheds Sutherland.⁸⁴

• In September, Rothesay announced it would raise an additional £500m in shareholder capital to support its longevity risk transfer business – which in 2019 alone executed around £10bn in new deals.

• In November, L&G agreed to provide annuities to Prudential (UK) customers with guaranteed rates. As part of the deal, all guaranteed benefits will be honoured by Prudential and fulfilled by L&G. Prudential (UK), while remaining a UK-registered business, is closing down its UK operations in favour of growing its business in the Far East.

• In November, PIC converted a £800m longevity swap – originally executed in 2017 with L&G – for a £750m buy-in for SSE on the back of improved funding for the pension scheme. This is the first example of a transfer of obligations between counterparties where the first counterparty (L&G) could have offered the buy-in itself. In novating the swap between counterparties, it is another important milestone in bringing an early form of liquidity to the longevity swaps market. The first conversion of a longevity swap to buy-in took place in 2017 and the SSE conversion is the fifth one to date. PIC said that a longevity swap provides a useful first step towards a buy-in.⁸⁵

• In November, Scottish Friendly bought the back-book of Canada Life’s 127,000 life and pensions policies, with assets under management increasing by £2.4bn as a result.

• A modest recovery in annuity sales following the big fall in sales after the “Freedom and Choice” reforms of 2015. There were 74,000 (internal and open market) annuity purchases in 2018/19. Annuity rates for 65-year-olds were 4%, which although low by historical standards, exceeded the 3% that a lower-risk fund offered as a sustainable withdrawal rate.⁸⁶

There are a number of reasons explaining the strength of the UK longevity risk transfer market in 2018 and 2019. First, funding levels have improved as a result of a) deficit reduction contributions and strong equity returns, which have increased asset values, and b) lower liability values due to a combination of higher interest rates and lower mortality improvements since 2011;⁸⁷ UK funds exhibited the first surplus in aggregate since 2011.⁸⁸ Second, there has been an increase in capital and competition from insurers which have recruited heavily and so have more staff to model pension scheme mortality, provide price quotations and implement transactions. Third, there has been an associated increase in reinsurance capacity, which is important since most of the longevity risk assumed by insurers is reinsured with global reinsurers. Fourth, there has been increasing standardisation of the models used to execute transfers, with three dominant examples: intermediated, pass through and captive. Fifth, insurers have been increasing their investment in high yielding illiquid matching assets, such as infrastructure, housing and urban regeneration, and equity release, and have passed on the additional yield (including illiquidity premium) to schemes in the form of lower prices. Sixth, greater certainty over how Solvency II reserving requirements operate has helped to reduce margins for prudence. Finally, once a scheme closes to new entrants, its maturity increases rapidly: the proportion of the scheme’s liabilities due to pensioners increases and the average age of non-pensioners also increases. Mature schemes tend to attract more favourable pricing because: scheme data for pensioners tends to be more reliable than for other types of member, there is less uncertainty over the timing and size of future cash flows, and the risk of the actual mortality experience deviating from that which was assumed is lower. All this helps to reduce the capital an insurer is required to hold.⁸⁹ Mercer have estimated that by 2030, more than £600bn of longevity risk transfers will have taken place in the UK, which represents more than one-third of the £1.5trn of UK pension fund assets.⁹⁰

Outside the UK, some significant longevity swaps took place, including:

• RGA Life Reinsurance Company of Canada, covering 45,000 Manulife Canadian annuitants (February).

• PartnerRe, covering 25,000 Manulife annuitants (March and May).

• Canada Life Re, €5.5bn, covering 150,000 in-payment and deferred pensioners liabilities of Dutch firm VIVAT (March).

• Canada Life Re, €12bn, for Dutch insurer Aegon (December).

Another innovation was the completion of a longevity swaption. Securis Investment Partners announced in January 2020 that they had completed a capital market derisking deal with a “large well-known life risk carrier”: “we have taken structured longevity risk on a specific block of business. The transaction was structured as an indemnity derisking tool, i.e., without the use of any longevity indices, as a way to optimise the impact for our counterparty even further. [It involved] a direct risk transfer to a Securis fund with no intermediary involved,…and was a first in terms of regulatory approval”.⁹¹

We had mentioned earlier the problem of capacity constraints in the insurance and reinsurance industries. Our conference series is explicitly about capital markets solutions to the problem of transferring longevity risk. When the modern form of the longevity risk transfer market started in 2006, investment banks, such as J.P.Morgan, with their links to capital market investors, were active in the market along with insurers. However, the Global Financial Crisis in 2008 and the 2010 US Dodd-Frank (Restoring American Financial Stability) Act which followed led to the majority of investment banks withdrawing from the market. A few banks with insurance subsidiaries – such as Goldman Sachs, owner of Rothesay Life, and Deutsche Bank, owner of Abbey Life – remained for a while before they too sold their life businesses. So for the past few years, the market has been dominated by insurers and reinsurers. However, they are beginning to see that the current growth rates in the market are not sustainable without new sources of external capital.

One new solution to this problem that has emerged recently is the reinsurance sidecar – which is a way to share risks with new investors when the latter are concerned about the ceding reinsurer having an informational advantage. Formally, a reinsurance sidecar is a financial structure established to allow external investors to take on the risk and benefit from the return of specific books of insurance or reinsurance business. It is typically set up by existing (re)insurers that are looking to either partner with another source of capital or set up an entity to enable them to accept capital from third-party investors (Bugler et al., 2020).

It is established as a SPV, with a maturity of 2–3 years. It is capitalised by specialist insurance funds, usually by preference shares, though sometimes in the form of debt instruments. It reinsures a defined pre-agreed book of business or categories of risk. Liability is limited to assets of the SPV and the vehicle is unrated. The benefit to insurers is that sidecars can provide protection against exposure to peak longevity risks,⁹² help with capital management by providing additional capacity without the need for permanent capital and can provide an additional source of income by leveraging underwriting expertise. The benefit to investors is that they enjoy targeted non-correlated returns relating to specific short-horizon risks and have an agreed procedure for exiting; investors can also take advantage of temporary price hikes, but without facing legacy issues that could affect an investment in a typical insurer.

There are a number of challenges to the use of sidecars in the longevity risk transfer market. There is the tension between the long-term nature of longevity risk and investor preference for a short-term investment horizon. There are also regulatory requirements on cedants, affecting their ability to generate a return. These include the posting of prudent collateral, the underlying assets in the SPV must generate matching cash flows, the risk transfer must be genuine and the custodian/trustee must be financially strong. There is also a risk to cedants of losing capital relief if regulatory requirements are not met or they change.

Three reinsurance sidecars were established at the end of 2017 and the beginning of 2018, with investment capital provided by private equity investors and hedge funds, in addition to insurers and pension funds.

In December, Athene entered into a reinsurance agreement with Voya Financial, covering $19bn of fixed, indexed and variable annuity liabilities. The matching assets will be managed by Athene Asset Management. Using an “enhanced asset management” strategy and positioning itself for “incremental value creation in a more favorable credit spread environment”, the company hopes to generate “mid-teens returns”. The capital is supplied mainly by private equity investors, including Apollo, Athene’s parent company, Crestview Partners and Reverence Capital Partners.⁹³

In January, RGA Re and RenaissanceRe announced a new start-up named Langhorne Re, which will target in-force life and annuity business. The new company has secured $780m of equity capital from RGA, RenaissanceRe and third-party sidecar investors, including pension funds and other life companies.⁹⁴

In February, the $400m Leo Re Ltd. 2018-1 collateralised reinsurance sidecar was executed between Dutch pension fund manager PGGM and Munich Re as a private ILS deal. The agreement allows PGGM, which manages the pension assets of the Dutch healthcare workers’ scheme, PFZW, to gain access to a share of Munich Re’s portfolio. PGGM will enter into direct ILS trades with counterparties, via quota share arrangements with a reinsurer, for a proportion of the counterparties’ underwriting book, thereby sharing in the cedents’ risks and underwriting returns.⁹⁵

In July, the island of Guernsey announced it would develop a simplified structure for the ILS market via an all-in-one legal entity that would combine insurance/reinsurance and investment activity in one vehicle – described as a “Fund of One”. This would create a more transparent vehicle for investors which would promote “true convergence” in ILS. Investors would establish both an unregulated investment fund and a reinsurance transformer cell. This would remove the need for multiple vehicles and allow a sidecar to have both the risks and the assets held in a single vehicle. This would help to reduce the challenges often associated with multiple vehicles, such as doing business in various jurisdictions, regulation, time zones, account rules, audit and multiple layers of administration expenses.⁹⁶

Another example of introducing new third-party capital is an initial public offer. This was the route Swiss Re considered in June 2019 when it proposed listing the shares of ReAssure – its UK closed book life consolidator business – on the London Stock Exchange. The idea was to provide working capital to put into new transactions and grow the UK life insurance book under the SwissRe brand. However, the idea was shelved due to weak demand and, in December 2019, ReAssure was sold to Phoenix for £3.2bn. In the process, Phoenix – which was valued at the time at £5.3bn – became Europe’s biggest consolidator of life and pension businesses and justified the acquisition on the grounds that “there are too many insurance companies in a market which is consolidating.[and the acquisition will] give us the opportunity to capture significant cost and capital synergies”.⁹⁷

In September 2019, the European Life Settlement Association launched the ELSA Master Agreement for Tertiary Transactions. The aim was to develop an industry standard purchase and sale agreement to make tertiary transactions more costs and time efficient – in a similar manner as the ISDA Master Agreement.⁹⁸

At the same time as these practical developments in the capital markets were taking place, academics were continuing to make progress on theoretical developments, building on the original idea of using longevity bonds to hedge longevity risk in the capital markets (Blake & Burrows, 2001). These included:

• Design and pricing of longevity bonds and other longevity-linked products (e.g. Blake et al., 2006a, 2006b, 2014; Bauer, 2006; Bauer & Ruß, 2006; Antolin & Bloomestein, 2007; Bauer & Kramer, 2007, Denuit et al., 2007; Barbarin, 2008; Bauer et al., 2010b; Chen & Cummins, 2010; Kogure & Kurachi, 2010; Bravo, 2011; Dowd et al., 2011a; Mayhew & Smith, 2011; Zhou et al., 2011, 2013; Chen et al., 2013; Shen & Siu, 2013; Denuit et al., 2015; Hunt & Blake, 2015; Milevsky & Salisbury, 2015; Yang et al., 2015; Wang & Li, 2016; Chen et al., 2017; Lin et al., 2017b ; Leung et al., 2018; MacMinn & Richter, 2018; Mayhew et al., 2020).

• Design and pricing of longevity-linked derivatives (e.g. Shang et al., 2011; Lin et al., 2013; Wang & Yang, 2013; Chuang & Brockett, 2014) and specifically survivor/longevity swaps (e.g. Dowd et al., 2006; Wang et al., 2013, 2015), survivor/longevity forwards and swaptions (e.g. Dawson et al., 2010), q-forwards (e.g. Deng et. al., 2012; Barrieu & Veraart, 2016), mortality options (e.g. Milevsky & Promislow, 2001; Zhou & Li, 2020), and guaranteed annuity options (e.g. Gao et al., 2015)

• Pricing longevity risk (e.g. Olivieri & Pitacco, 2008; Bayraktar et al., 2009; Chen et al., 2010; Li, 2010).

• The pricing of longevity-related guarantees (e.g. Yang et al., 2008)

• The pricing and hedging of life settlements (e.g. Deng et al., 2011; Brockett et al., 2013; Zhu & Bauer, 2013; MacMinn & Zhu, 2017)

• Longevity and mortality indices (e.g. Denuit, 2009; Li et al., 2011; Chan et al., 2014; Tan et al., 2014)

• Securitisation of longevity risk (e.g. Dahl, 2004; Chen & Cox, 2009; Cowley & Cummins, 2005; Lin & Cox, 2005; Cairns et al., 2006a; Cox & Lin, 2007; Biffis & Blake, 2010; 2013, 2014; Wills & Sherris, 2010; Lane, 2011; Mazonas et al., 2011; Blake et al., 2013; Yang & Huang, 2013; Michaelson & Mulholland, 2014; Li et al., 2017; MacMinn & Brockett, 2017; Bugler et al., 2020)

• Management and hedging of longevity risk (e.g. Dahl & Møller, 2006; Friedberg & Webb, 2007; Cocco & Gomes, 2008; Tsai et al., 2010; Wang et al., 2010; Coughlan et al., 2011; Koijen et al., 2011; Li & Hardy, 2011; Tzeng et al., 2011; Wang et al., 2010; 2011b; Ngai & Sherris, 2011; Barrieu et al., 2012; International Monetary Fund, 2012; Li & Luo, 2012; Cairns, 2013; Cox et al., 2013a, 2013b; Qiao & Sherris, 2013; Cairns et al., 2014; Zelenko, 2014; Zhu & Bauer, 2014; Li et al., 2017a; Wong et al., 2017; Zhou & Li, 2017; D’Amato et al., 2018; Liu & Li, 2016, 2018; Hanbali et al., 2019; Kessler, 2020; Cairns & El Boukfaoui, 2020; Hsieh et al., 2020; Li et al., 2020; Liu & Li, 2020; MacMinn & Zhu, 2020)

• Mortality modelling, mortality term structure⁹⁹ modelling and mortality forecasting (e.g. Heligman & Pollard, 1980; Hobcraft et al., 1982; Alho, 1990; Lee & Carter, 1992; Thatcher et al., 1998; Wilmoth & Horiuchi, 1999; Booth et al., 2002a, 2002b; Brouhns et al., 2002a, 2002b, 2005; Renshaw & Haberman, 2003a, 2003b, 2006, 2008; Currie et al., 2004; Biffis, 2005; Bongaarts, 2005; Czado et al., 2005; Cairns et al., 2006b, 2008, 2009, 2011a; De Jong & Tickle, 2006; Delwarde et al., 2007; Koissi et al, 2006; Pedroza, 2006; Bauer et al., 2008; Blake et al., 2008; Gourieroux & Monfort, 2008; Hari et al., 2008; Kuang, et al., 2008; Haberman & Renshaw, 2009, 2011, 2012, 2013; Hatzopoulos & Haberman, 2009, 2011; Li et al., 2009, 2013, 2015a, 2015b, 2017b; Plat, 2009a, 2009b; Wang & Preston, 2009; Bauer et al., 2010a; Biffis & Blake, 2010; Biffis et al., 2010; Cox et al., 2010; Debonneuil, 2010; Dowd et al., 2010a, 2010b; Lin & Tzeng, 2010; Murphy, 2010; Yang et al., 2010; Coelho & Nunes, 2011; Currie, 2011, 2016; D’Amato et al., 2011, 2012a, 2012b; Ediev, 2011; Gaille & Sherris, 2011; Li & Chan, 2011; Milidonis et al., 2011; Russo et al., 2011; Russolillo et al., 2011; Sweeting, 2011; Wang et al., 2011a; Yue & Huang, 2011; Zhu & Bauer, 2011; Alai & Sherris, 2014b; Aleksic & Börger, 2012; Hainaut, 2012; O’Hare & Li, 2012, 2017; Wilmoth et al., 2012; Hyndman et al., 2013; Kleinow & Cairns, 2013; Mitchell et al., 2013; Nielsen & Nielsen, 2014; Hunt & Blake, 2014, 2020a, 2020b, 2020c, 2020d; Villegas & Haberman, 2014; Danesi at al., 2015; Tomas & Planchet, 2015; Leng & Peng, 2016; Schinzinger et al., 2016; van Berkum et al., 2016; Beutner et al., 2017; Deprez et al., 2017; Kleinow & Richards, 2017; Li & Lu, 2017; Li & O’Hare, 2017; Milidonis & Efthymiou, 2017; Neves et al., 2017; Shang & Hyndman, 2017; Tsai & Lin, 2017; Börger & Schupp, 2018; Debonneuil et al., 2018; Hainaut, 2018; McCarthy, 2018; Salhi & Thérond, 2018; Hilton et al., 2019; Boumezoued, 2020; Guo & Bauer, 2020; McCarthy & Wang, 2020; Su & Yue, 2020; Venter & Şahln, 2018; Yue et al., 2020)

• Multi-population mortality modelling (e.g. Darkiewicz & Hoedemakers, 2004; Li & Lee, 2005; Cairns et al., 2011b; Dowd et al., 2011b; Jarner & Kryger, 2011; Njenga & Sherris, 2011; Börger & Ruß, 2012; Torri & Vaupel, 2012; D’Amato et al., 2014; Raftery et al., 2014; Zhou et al., 2014; Chen et al., 2015; Kleinow, 2015; Biffis et al., 2017; Li et al., 2015c, 2017; De Jong et al., 2016; Enchev et al., 2017; Zhu et al., 2017; Hunt & Blake, 2018; Pascariu et al., 2018; Wang et al., 2018; Yang et al., 2020; Chang et al., 2020)

• Cause-of-death mortality modelling (e.g. Beard, 1971; McNown & Rogers, 1992; Christensen & Vaupel, 1996; Hanewald, 2011; Murphy & Di Cesare, 2012; Alai et al., 2014; Arnold & Sherris, 2015; Gourieroux & Lu, 2015; Alai et al., 2018; Boumezoued et al., 2018; Yue et al., 2018; Li et al., 2019; Lyu et al., 2020)

• Longevity risk and financial innovation (improvements in the analysis and design of longevity-linked products) (e.g. Gong & Webb, 2010; Stevens at al., 2010; Richter & Weber, 2011; Cocco & Gomes, 2012; Brown & Warshawsky, 2013; Bernhardt & Donnelly, 2019)

• Reverse or ERMs (e.g. Wang et al., 2008; Huang et al., 2011; Yang, 2011; Alai et al., 2014a; Kogure et al., 2014; Shao et al., 2015; Lee et al., 2018)

• Longevity risk in investment portfolios (e.g. Milevsky & Young, 2007; Menoncin, 2008; Horneff et al., 2008, 2009, 2010, 2015; Huang et al., 2012; Maurer et al., 2013; Aro & Pennanen, 2017; Rogalla, 2020)

• Longevity risk in pension plans, pension systems and annuities (e.g. Aro, 2014; Bisetti & Favero, 2014; Donnelly, 2014; Lin et al., 2014, 2015, 2017a; Ai et al., 2015; Wan & Bertschi, 2015; Ai et al., 2017; Bravo & El Mekkaoui de Freitas, 2018; Bruszas et al., 2018; Cox et al., 2018; Hsieh et al., 2018; Kurtbegu, 2018; Mayhew et al., 2018; Cox et al., 2020; Dowd et al., 2020)

• Longevity inequality (e.g. Mayhew & Smith, 2014, 2020; Debón et al., 2017; Sanzenbacher et al., 2020).

As mentioned before, not all paths to progress are smooth. In recent years, this has been particularly true currently in the largest market dealing with micro-longevity risk, namely life settlements.¹⁰⁰ The life settlements market has been dogged by systematic underestimates of policy holders’ life expectancies by certain medical underwriters, issues concerning premium financing, frauds and ethical issues associated with “profiting” from individuals dying and policies maturing. In December 2009, Goldman Sachs announced it was closing down its QxX.LS index. This was partly because of the reputational issues associated with life settlements, but mainly because of insufficient commercial activity in the index. While the ethical issues are no different in substance from those relating to the macro-longevity market (see, e.g. Blake & Harrison, 2008), the micro-longevity market needs to learn some important lessons from the macro-longevity market. The macro-longevity market has been very successful at promoting good basic research on the analysis of the stochastic mortality forecasting models it uses and putting these models into the public domain and has also been much more transparent with the data it uses. This suggests a way forward for the life settlements micro-longevity market.

Another setback, this time to the macro-longevity market, occurred in April 2012 when a number of investment banks – Credit Suisse, Nomura and UBS – pulled out of the longevity risk transfer market as a result of additional capital requirements under Basel III. Investment banks had already been disadvantaged in this market by the Dodd-Frank Act which prevented US banks and their affiliates from entering longevity swaps and synthetic trades in life settlements. At around the same time, however, a number of insurers and reinsurers entered the market, that is, PICA, SCOR and Munich Re. The following year witnessed the start of a process of consolidation in the insurance industry. In August 2013, Lucida was purchased by L&G for £150m; at that time, it had 31,000 pensioners on its books and £1.4bn in pension assets. In February 2014, the buyout business of MetLife, which entered the market in 2007 and acquired the pension assets of 20,000 pensioners worth £3bn, was sold to Rothesay Life for an undisclosed sum, bringing its total assets to £10bn.

In December 2013, Goldman Sachs sold the majority of its stake in Rothesay Life to Blackstone (28.5%), Government of Singapore Investment Corporation (28.5%) and MassMutual (7%), due to the new regulatory capital requirements faced by banks and insurers.¹⁰¹

In 2016, the UK Office for National Statistics (ONS) reported that longevity improvements rates at very high ages have slowed down since 2011. A number of reasons were put forward to explain this: short-term reasons, such as lower increases in health service and long-term care spending as part of the government’s “austerity” spending cuts following the 2008–09 Global Financial Crisis; and longer-term reasons, such as the fact that most of the improvement in life expectancy in the 1990s and 2000s was due to lower mortality from circulatory causes, such as heart disease, and there was no longer scope for further improvements.¹⁰² In 2018, the UK ONS reported that healthy life expectancy – the average number of years lived in “very good” or “good” general health – fell for women and rose for men, comparing 2015–17 and 2009–11 data. For men, healthy life expectancy at birth increased by 5 months to 63.1 years, while it fell by 3 months to 63.6 years for women. At birth, UK men and women can expect to live with a disability for 16.5 and 20.9 years, respectively.¹⁰³

This prompted a debate in the UK about the reliability of life expectancy projections. Mortality improvements in UK males averaged 0.6% p.a. over the preceding 4 years, compared with 3.2% p.a. in the decade before and 1.5–2% between 1995 and 2000. The most recent view of the UK actuarial profession is that the reduction in the trend improvement is permanent. The Mortality Projections Model of the IFoA's Continuous Mortality Investigation (CMI) – which covers England & Wales – published in March 2019 showed that the average cohort life expectancy of a 65-year old man in 2018 was 19.8 years, down by 5 months (or 2.4%) compared with 2017; the corresponding figure for a 65-year old woman was 22.4 years, also down by 5 months (or 2.1%).¹⁰⁴ US male life expectancy has also been declining between 2015 and 2016 from 76.3 to 76.1 years. The main causes were unintentional injuries (due to drug, mainly opioid, overdoses), death from Alzheimer’s and suicides. Female life expectancy remained constant at 81.1 years. Time will tell if this indeed a permanent change in trend or if the trend will again reverse in response to advances in applied biotechnology and in molecular and regenerative medicine. The most recent evidence from CMI published in December 2018 comes from their Self-Administered Pension Scheme (SAPS) data set. This covers UK members of DB pension schemes and the data have been collected since 2000. The S3 series mortality tables for the period 2009–16 showed that life expectancy in this select group was still increasing when compared with the S2 series mortality tables for the period 2004–11.¹⁰⁵

These developments are part of an emerging global debate covering a wider set of demographic issues than just longevity risk. The debate has centred on population ageing and its implications. One aspect of population ageing is declining fertility which soon translates into an increase in the average age of the population. One reason for declining fertility is the choice made by women in developed countries to have fewer children than previous generations. But another is male sperm counts falling so fast across the world that the human race could be infertile within 50 years. There has been a 60% decline in the sperm count of Western men between 1973 and 2011, with 15% of young Western men with a sperm count low enough to impair fertility. A variety of explanations have been put forward to explain this: lifestyle factors, such as alcohol, smoking, stress, obesity, antidepressants and high doses of ibuprofen; pesticides and industrial pollutants getting into the food chain; sunscreen, containing endocrine-disrupting UV filters; non-stick frying pans, containing poly- and perfluoroalkyl substances; tight pants; oestrogen in the water supply from the female contraceptive pill; and electromagnetic radiation from Wi-Fi routers.¹⁰⁶

Another aspect of population ageing is the differential impact on the rich and poor. A recent study by the Longevity Science Panel in the UK found that, while life expectancy had increased for all socio-economic groups between 2001 and 2015, it increased most for the richest cohort. The difference in life expectancy was 7.2 years in 2001, but this had increased to 8.4 years in 2015.¹⁰⁷ Another study found that, while socio-economic status affects the incidence of multimorbidity (two or more of diabetes, coronary heart disease, stroke, chronic obstructive pulmonary disease, depression, arthritis, cancer, dementia and Parkinson’s disease), it did not affect the risk of mortality after the onset of these adverse health conditions, implying that primary prevention is key to reducing social inequalities in mortality (Dugravot et al., 2019). These findings will have implications for fairness between different cohorts of the same generation, for example, when governments raise the retirement age for all in response to increasing life expectancy. In response to these inequalities, the government set up the UK Longevity Council to advise it on how best to use innovations in technology products and services to improve the lives of the older population. With the number of people in the UK over the age of 65 years to double to more than 20 million over the next half century, the government has set itself the Ageing Society Grand Challenge which aims to ensure that people in the UK enjoy an extra 5 years of healthy and independent living by 2035, while narrowing the gap between the experience of the richest and poorest.¹⁰⁸ Some of these issues do not immediately affect the longevity risk transfer market, but they might do in due course, so it is important to flag them now.

There are other global developments that could affect life expectancy, positively or negatively. On the positive side, examples include (1) Steve Horvath (UCLA) and Ken Raj (Public Health England) have demonstrated that rapamycin retards epigenetic ageing of human cells – using an epigenetic clock (called the Skin and Blood Clock) which is an accurate biomarker for ageing that relies on the mathematical precision of the relationship between chemical modifications on DNA called methylation and changes in age;¹⁰⁹ (2) potential reversal of ageing using a younger person’s blood, flowing successful experiments with mice;¹¹⁰ (3) Randall J. Bateman (Washington University School of Medicine in St. Louis) has developed a simple blood test that can detect Alzheimer’s disease in its earliest stages by measuring levels of the protein amyloid beta which begin to collect in the brain 15 to 20 years before symptoms arise and play a key role in the development of Alzheimer’s disease;¹¹¹ (4) identification of an inflammatory marker called sCD14 which is linked to cognitive decline and dementia, allowing early intervention;¹¹² (5) identification of a biomarker for tumour initiating (or cancer stem) cells;¹¹³ (6) the development of protein-destroying drugs, capable of degrading the MYC cancer-fuelling protein or the tau protein responsible for Alzheimer’s disease;¹¹⁴ the Institute of Ageing at Newcastle University and the Mayo Clinic in the US have demonstrated that killing senescent cells – which have stopped dividing and hence renewing themselves and so have lost their purpose but can destabilise neighbouring cells and promote low-level inflammation – can be selectively killed (using a process known as senolytics) and this helps to postpone multiple age-related disabilities and disease;¹¹⁵ (7) the development of CRISPR technology for editing genomes allows scientists to change DNA sequences and modify gene function, so that, for example, genetic defects can be corrected and the spread of diseases can be prevented; and (8) using artificial intelligence to correct faults in the human nervous system, for example, robotic arms controlled by brain signals replacing lost human arms.¹¹⁶ These developments led Bank of America to conclude that the human lifespan could soon pass 100 years, with one of the biggest investment opportunities over the next decade being in companies working to delay human death, a market expected to be worth at least $600bn by 2025.¹¹⁷ Dr Nir Barzilai, founding director of the Institute for Aging Research at the Albert Einstein College of Medicine, New York, argues that “Death is inevitable but ageing is not”.¹¹⁸ On the negative side, examples include (1) an increase in deaths from heart and circulatory diseases in the UK for the first time in 50 years – as a result of an increase in obesity and type 2 diabetes;¹¹⁹ and (2) the World Economic Forum’s Global Risks Report 2019 warns of increasing naturally emerging infectious disease pandemics and risks posed by revolutionary new biotechnologies, claiming that these pose as big a threat as climate change.¹²⁰

A number of insurers and reinsurers have used the capital markets to securitize some of the mortality risk on their book of business, in the form of what have become known as mortality-linked (or mortality catastrophe) bonds – see Table 1. Swiss Re has been the most active participant in the market, issuing the first security in 2003, known as Vita I.¹²¹ Vita I was a $400m principal-at-risk variable rate note, where the investors’ principal was at risk in certain extreme mortality risk scenarios in exchange for quarterly coupon payments of USD 3-month Libor plus a spread of 135 basis points. The bond matured on 1 January 2007.

Table 1. Mortality-linked bonds, 2003–2020

Source: https://www.artemis.bm/deal-directory/

As with the previous conferences, Longevity 14 consisted of both academic papers and more practical and policy-oriented presentations. There were six plenary sessions: mortality trends and forecasts, how much intergenerational risk sharing is optimal?, using risk analytics and state-of the-art technology to optimise the value of a PRT business and the practical application of longevity research, stimulating the longevity index market, and longevity investments and the regulatory dimension. The following keynote speakers and panellists contributed to these sessions:

• Professor James Vaupel (AXA Professor of Longevity Research and Director of the Interdisciplinary Center for Research and Education on Population Change at the University of Southern Denmark) gave the opening presentation entitled “Longevity: Past and future”. He argued that extrapolation was a better way of predicting life expectancy than actuarial forecasts, highlighting longevity-boosting developments such as potential treatments for cancer and ageing, as well as the rejuvenation of skin and organs.

• Peter Banthorpe (Senior Vice President and Head of Global Research and Development with RGA Reinsurance Company) discussed “Mortality trends and forecasts across the UK, US, and Canadian Markets”.

• Michel Vellekoop and Wilbert Ouburg (Dutch Actuarial Society) gave a presentation on “Increasing the stability of mortality projections: the Dutch approach”.

• Peter Vlaar (Senior Strategist ALM, APG) discussed “The ever lasting Dutch pension debate: How much collectivity do we want to keep?”

• Professor Michel Vellekoop (Professor in Actuarial Sciences and Mathematical Finance, Universiteit van Amsterdam) spoke about “Longevity risk sharing in collective pension schemes: current practice and proposals for alternatives”.

• Amy Kessler (Senior Vice President and head of Longevity Risk Transfer, Prudential Financial, Inc.) gave a presentation entitled “Everybody out of the pool: Optimizing outcomes if there is a shift from a collective to an individual pension risk system”.

• Jeff Mulholland (Managing Director, PwC) talked about “Using risk analytics to optimize the value of a pension risk transfer business” and discussed practical applications of state-of-the-art longevity research.

• Mark Higgins (Chief Operating Officer, Beacon) presented on “Technology solutions for optimizing the value of a pension risk transfer business”.

• Guy Coughlan (Chief Risk Officer, USS) gave a talk on “Inequality: Wealth, health and longevity”.

• Sarah Bates (Former Chair of St. James’s Place Wealth Management) spoke about “Intergenerational wealth transfers, social inequality and immobility”.

• Douglas Anderson (Founder, Club Vita) talked about “Completing the circle: Overcoming the final hurdles to stimulating the longevity index market”.

• Cord-Roland Rinke (Managing Director, Hannover Re) discussed “A new framework for longevity index covers”.

• Avery Michaelson (Founding Partner, Longitude Solutions) considered “Increasing longevity investment opportunities for capital markets investors”.

• Leendert van Gastel (Solvency Supervisor, Netherlands National Bank) spoke about “Longevity risk mitigation from a supervisory perspective”.

The academic papers that were selected by us as the editors of this Special Issue went through a refereeing process subject to the usual high standards of the Annals of Actuarial Science. They cover the following themes: longevity hedging, annuities and other pension products, demographic inequalities in mortality, mortality data reliability in internal models, mortality models, and identifiability in mortality models. We briefly discuss each of the 12 papers selected.

In “Longevity trend risk over limited time horizons”, Stephen J. Richards, Iain D. Currie, Torsten Kleinow and Gavin Ritchie consider various aspects of longevity trend risk viewed through the prism of a finite time window. They point out that Solvency II in the European Union, and similar regulations elsewhere, specify a value-at-risk (VaR) approach to solvency assessment. Other territories specify regulations based around conditional tail expectations (CTEs), also known as tail-VaR (tVaR). Both solvency approaches view risk over a 1-year horizon, and both calculations can be performed using the same sample data. The authors show the broad equivalence of VaR capital requirements at a p-value of 99.5% to (CTEs) at 99%. They also show how deferred annuities have higher risk, which can require double the solvency capital of equivalently aged immediate annuities. However, results vary considerably with the choice of model, and so longevity trend-risk capital can only be determined through consideration of multiple models to inform actuarial judgement. This model risk is even starker when trying to value longevity derivatives. The authors briefly discuss the importance of using smoothed models and describe two methods to considerably shorten VaR and CTE run times.

Kenneth Q. Zhou and Johnny Siu-Hang Li argue in “Asymmetry in Mortality Volatility and its Implications on Index-based Longevity Hedging” that mortality volatility is crucially important to many aspects of index-based longevity hedging, including instrument pricing, hedge calibration and hedge performance evaluation. Their paper sets out to develop a deeper understanding of mortality volatility and its implications on index-based longevity hedging. First, they study the potential asymmetry in mortality volatility by considering a wide range of GARCH-type models that permit the volatility of mortality improvements to respond differently to positive and negative mortality shocks. They then investigate how the asymmetry of mortality volatility may impact index-based longevity hedging solutions by developing an extended longevity Greeks framework, which encompasses longevity Greeks for a wider range of GARCH-type models, an improved version of longevity vega, and a new longevity Greek known as “dynamic delta”. The theoretical work is complemented by two real-data illustrations, the results of which suggest that the effectiveness of an index-based longevity hedge could be significantly impaired if the asymmetry in mortality volatility is not taken into account when the hedge is calibrated.

In “Optimal Portfolio Choice with Tontines under Systematic Longevity Risk”, Irina Gemmo, Ralph Rogalla and Jan-Hendrik Weinert derive optimal portfolio choice patterns in retirement (aged 66 to 105 years) for a constant relative risk aversion utility-maximising investor facing risky capital market returns, stochastic mortality risk and income-reducing health shocks. Beyond the usual stocks and bonds, the individual can invest his assets in tontines. Tontines are cost-efficient financial contracts providing age-increasing, but volatile cash flows, generated through the pooling of mortality without guarantees, which can help to match increasing financing needs at old ages. The authors find that a tontine invested in the risk-free asset dominates stock investments for older investors without a bequest motive. However, with a bequest motive, it is optimal to replace the tontine investment over time with traditional financial assets. The results indicate that early in retirement, a tontine is only an attractive investment option, if the tontine funds are invested in a risky asset. In this case, they crowd out stocks and risk-free bonds in the optimal portfolios of younger investors. Over time, the average optimal portfolio weight of tontines decreases. Introducing systematic mortality risks noticeably reduces the peak allocation to tontines.

In “Linking Annuity Benefits to the Longevity Experience: Alternative Solutions”, Annamaria Olivieri and Ermanno Pitacco argue that uncertainty about financial returns and life expectancy, combined with reduced social security benefits, increasingly expose individuals to the risk of outliving their post-retirement assets. However, the demand for longevity guarantees remains low, due to high costs. The providers, on their side, may be reluctant to offer nonadjustable longevity guarantees, as the risk is long-term and difficult to predict. It is therefore convenient to reconsider the design of longevity guarantees. In particular, a participating structure, providing a link to some longevity experience, could allow a sharing of losses, and possibly profits, resulting in a reduction of the cost of the retained guarantee. The literature has proposed a number of alternatives to define a longevity linking arrangement, but the topic is not yet completely explored. It is useful, in particular, to have a common framework, under which the various solutions can be interpreted and compared, also with a view to the trade-off between the retained risk and the cost of the guarantee. The main purpose of the paper is to develop a general structure describing longevity-linked post-retirement benefits is. Allowing for aggregate longevity risk, the authors then examine suitable solutions for insurance products.

Anne G. Balter, Malene Kallestrup-Lamb and Jesper Rangvid point out in “Variability in Pension Products: A Comparison Study between the Netherlands and Denmark” that the Danish and Dutch pension systems are, according to the Melbourne Mercer Global Pension Index “among the best in the world” in terms of adequacy (the size of pension savings), integrity (the governance of the pension providers) and the overall sustainability (coverage, assets, contributions and demography) of the pension system.¹²² In spite of large pension savings, both systems face challenges. Key ones are the current low interest rate environment coupled with increasing life expectancy which makes it increasingly difficult for pension providers to honour promised (and certainly guaranteed) pensions. As a consequence, both sectors have undergone and are undergoing considerable change. The authors compare the two countries’ pension systems and pension products. They focus on the shifts that have taken place, from pension products with relatively low levels of risk for the participant, to pension products with more risk but also higher expected return. They end by drawing lessons that are relevant for discussions in many countries.

In “An Investigation into the Impact of Deprivation on Demographic Inequalities in Adults”, Les Mayhew, Gillian Harper and Andrés M. Villegas investigate the impact of deprivation on demographic inequalities in England and Wales among adults. Using demographic measures, including the modal age at death, life expectancy, lifespan variation and mortality, the authors show a negative correlation with deprivation as measured by the 2015 Index of Multiple Deprivation. Although the study finds that life expectancy is increasing overall and the gap between men and women is narrowing, improvements are slower paced in more deprived areas and the gap between rich and poor is slowly worsening over time. Men are more adversely impacted by deprivation than women with the gap in period life expectancy at the age of 30 years in 2015 between the top and bottom 1% of deprived neighbourhoods at 10.9 years for men and 8.4 years for women. Between 2001 and 2015, inequalities in male mortality rates at the age of 44 years were 4.4 times greater in the most deprived 10% of neighbourhoods than those in the 10% least deprived and were much higher than in intervening deciles. The worst deprivation is concentrated in specific areas. For example, in 22 out of 326 English districts, 25% or more of neighbourhoods are in the most deprived 10% and in 5 districts it is 40% or above.

The paper on “Mortality in the US by Education Level” by Cristian Redondo Lourés and Andrew J.G. Cairns, recognising the differences in mortality rates by socio-economic group, uses a variety of data sources, including highly detailed cause-of-death data from the United States Centers for Disease Control and Prevention, to explore the mortality gap between the better and worse off in the US during the period 1989–2015, using education as a proxy.

In “Mortality data reliability in an internal model”, Fabrice Balland, Alexandre Boumezoued, Laurent Devineau, Marine Habart and Tom Popa discuss the impact of some mortality data anomalies on an internal model capturing longevity risk in the Solvency II framework. In particular, the authors are concerned with abnormal cohort effects such as those for the generations born in 1919 and 1920, for which the period tables provided by the Human Mortality Database show particularly low and high mortality rates, respectively. To provide corrected tables for three countries of interest (France, Italy and West Germany), the authors use the approach developed by Boumezoued (2020) for two countries with reliable monthly fertility data (France and Italy) and provide an extension of the approach for West Germany where monthly fertility data are not sufficient to cover the generations of interest. These mortality tables are crucial inputs to stochastic mortality models forecasting future scenarios, from which the extreme 0.5% longevity improvement can be extracted, allowing for the calculation of the SCR. More precisely, to assess the impact of such anomalies in the Solvency II framework, the authors use a simplified internal model based on three common stochastic models to project mortality rates in the future combined with a closure table methodology for older ages. Correcting this bias obviously improves the data quality of the mortality inputs, which is of paramount importance today, and slightly decreases the capital requirement. Overall, the longevity risk assessment remains stable, as well as the selection of the stochastic mortality model. As a collateral gain of this data quality improvement, the more regular estimated parameters allow for new insights and a refined assessment regarding longevity risk.

The aim of “CBDX: A Workhorse Mortality Model from the Cairns-Blake-Dowd Family”, by Kevin Dowd, Andrew J.G. Cairns and David Blake, is to identify a workhorse mortality model for the adult age range (i.e. excluding the accident hump and younger ages). It applies the “general procedure” (GP) of Hunt & Blake (2014) to identify an age-period model that fits the data well before adding in a cohort effect that captures the residual year-of-birth effects arising in the original age-period model. The resulting model is intended to be suitable for a variety of populations, but economises on the number of period effects in comparison with a full implementation of the GP. The authors estimate the model using two different iterative maximum likelihood (ML) approaches – one Partial ML and the other Full ML – that avoid the need to specify identifiability constraints.

In “Identifiability in Age/Period Mortality Models”, Andrew Hunt and David Blake argue that as the field of modelling mortality has grown in recent years, the number and importance of identifiability issues within mortality models has grown in parallel. This has led both to robustness problems and to difficulties in making projections of future mortality rates. In this paper, the authors present a comprehensive analysis of the identifiability issues in age/period mortality models in order to first understand them better and then to resolve them. To achieve this, they discuss how these identifiability issues arise, how to choose identification schemes which aid our demographic interpretation of the models and how to project the models so that our forecasts of the future do not depend upon the arbitrary choices used to identify the historical parameters estimated from historical data.

In a companion paper, “Identifiability in Age/Period /Cohort Mortality Models”, Andrew Hunt and David Blake show that the addition of a set of cohort parameters to a mortality model can generate complex identifiability issues due to the collinearity between the dimensions of age, period and cohort. These issues can lead to robustness problems and difficulties making projections of future mortality rates. Since many modern mortality models incorporate cohort parameters, the authors believe that a comprehensive analysis of the identifiability issues in age/period/cohort mortality models is needed. In this paper, they discuss the origin of identifiability issues in general models before applying these insights to simple but commonly used mortality models. They then discuss how to project mortality models.

Finally, in “Constraints, the Identifiability Problem and the Forecasting of Mortality”, Iain D. Currie points out that models of mortality often require constraints in order that parameters may be estimated uniquely. He argues that it is not difficult to find references in the literature to the “identifiability problem” and papers often give arguments to justify the choice of particular constraint systems designed to deal with this problem. Many of these models are generalised linear models and it is known that the fitted values (of mortality) in such models are identifiable, that is, invariant with respect to the choice of constraint systems. The author shows that for a wide class of forecasting models, namely ARIMA(p; $\delta$ ; q) models with a fitted mean and $\delta=1$ or 2, identifiability extends to the forecast values of mortality; this extended identifiability continues to hold when some model terms are smoothed. The results are illustrated with data on UK males from the ONS for the age-period model, the age-period-cohort model, the age-period-cohort-improvements model of the CMI and the Lee–Carter model.

Longevity 15 took place in Washington DC on 12–13 September 2019. Insurance: Mathematics and Economics will publish a Special Issue of selected papers presented at this conference. Longevity 16 will take place in Singapore on 9–10 September 2021. The Journal of Demographic Economics will publish a Special Issue of selected papers presented at this conference. Longevity 17 will take place in Copenhagen in 2022 and Longevity 18 will take place in Toronto in 2023.