Application of bivariate negative binomial regression model in analysing insurance count data

Abstract

In this paper we analyse insurance claim frequency data using the bivariate negative binomial regression (BNBR) model. We use general insurance data on claims from simple third-party liability insurance and comprehensive insurance. We find that bivariate regression, with its capacity for modelling correlation between the two observed claim counts, provides both a superior fit and out-of-sample prediction compared with the more common practice of fitting univariate negative binomial regression models separately to each claim type. Noting the complexity of BNBR models and their potential for a large number of parameters, we explore the use of model shrinkage methodology, namely the least absolute shrinkage and selection operator (Lasso) and ridge regression. We find that models estimated using shrinkage methods outperform the ordinary likelihood-based models when being used to make predictions out-of-sample. We find that the Lasso performs better than ridge regression as a method of shrinkage.

1. Introduction

We explore the use of a bivariate negative binomial regression (BNBR) model in the context of modelling bivariate insurance claim frequency data. Two types of insurance claims, the third-party liability claim and the comprehensive cover claim, made by the same policyholder are assumed to be correlated and to be explained by a set of explanatory variables. By allowing a correlation between the two response variables, the performance of the BNBR is better than if two univariate negative binomial regression (UNBR) models are fitted separately, both in terms of in-sample goodness-of-fit and out-of-sample prediction. We also find that the BNBR also outperforms the bivariate Poisson regression (BPR) model.

In addition, we apply two shrinkage techniques, the least absolute shrinkage and selection operator (Lasso) and ridge regression, to reduce the number of covariates used in the original unshrunken BNBR model. Although an increasing number of explanatory variables will increase in-sample goodness-of-fit, an overfitted model may result which performs less well in out-of-sample prediction. By selecting more relevant risk factors and removing unnecessary explanatory variables, we find that the shrunken models outperform the unshrunken model in out-of-sample prediction.

We use the model specification for BNBR in Famoye (2010 b ), where correlation structure allows for both a negative and a positive relationship between the two claim type frequencies.

The contributions of this paper are threefold. First, we successfully demonstrate the importance of the BNBR model in analysing over-dispersed general insurance claim data, which outperforms the BPR model. Second, the correlation factor is found to be significant, with the implication that BNBR model is more suitable when the two claim counts are correlated. A similar conclusion is not evident in Famoye (2010 b ), where the correlation between the two variables considered is too low for useful dependence modelling, and thus univariate models seem to be adequate. Third, we shrink both BNBR models and UNBR models to reduce the size of coefficients of irrelevant explanatory variables, some of which are eliminated totally from the regression model. The shrinkage results are consistent with James et al. (2013: Chapter 6), in that the shrunken models provide much higher out-of-sample prediction accuracy, compared with the original full BNBR models.

The paper is organised as follows: section 2 gives a summary of existing methods to analyse claim counts, including univariate and bivariate generalised linear models (GLMs). Section 3 describes the model used in this study as well as the shrinkage techniques. Section 4 introduces the claims data. Section 5 gives the modelling results and a discussion of findings. Section 6 concludes the paper.

2. Literature Review

Modelling of insurance claim count data has been an active area of research for some decades. The research interest often lies in modelling the relationship between the observed counts and a set of explanatory variables. GLMs are very commonly used for this purpose as a mathematical formulation of the relationship. With a chosen link function, the mean of the distribution can be expressed as a linear function of the explanatory variables.

Under the GLM framework, the response variable is modelled using a member of the exponential dispersion family of distributions. Two common choices for this distribution in the case of insurance count data are the Poisson distribution and the negative binomial distribution (see McCullagh & Nelder, 1989). While the Poisson regression model assumes equality between the underlying mean and variance of the response variable, negative binomial regression relaxes the assumption and accounts for over-dispersion in the data (see Cameron & Trivedi, 2005). Both models have been widely adopted to analyse claim count data in general insurance. For example, Dionne & Vanasse (1989) used both Poisson and negative binomial regression models for automobile insurance risk classification. Haberman & Renshaw (1996) illustrated the use of the over-dispersed Poisson model in analysing life insurance claim counts, after presenting a summary of GLMs in actuarial science. Some other early studies in this area are Samson & Thomas (1987), Hürlimann (1990) and Renshaw (1995).

Various extensions to the basic GLM framework have been proposed in the statistics literature and explored in insurance contexts. For example, generalised additive models (GAMs) are postulated by combining an original GLM with additive models in the linear regression model, where smooth functions with semi-parametric or non-parametric forms are applied to explanatory variables. So with a chosen link function, the mean of the response variable is expressed as a linear function of unknown smooth functions of explanatory variables (see Hastie & Tibshirani, 1990). The GAM framework is adopted in Denuit & Lang (2004) to account for discrete, continuous and spatial risk factors in a Bayesian framework for insurance rate-making purposes. Mixtures of GLMs, such as Poisson mixtures, can be used to accommodate non-homogeneous populations (see Karlis & Xekalaki, 2005). More recently, increasing attention has been given to the application of extended GLMs in accounting for excess zero and over-dispersion in count data, especially for automobile insurance count numbers under no claim discount system. The proposed zero-inflated models are considered as a mixture of zero point mass and a Poisson or negative binomial regression models under the original GLM framework. Yip & Yau (2005) provided a good summary of zero-inflated models with an application in general insurance count data. Heller et al. (2007) considered a group of candidate distribution to model claim counts, including Poisson, zero-inflated Poisson and negative binomial. Thorough reviews for count data regression can be found in Denuit et al. (2007) and Cameron & Trivedi (1998).

In addition to univariate models, bivariate regression models have been proposed to analyse two response variables that are possibly correlated. These models offer sufficient flexibility by allowing the two response variables to be affected by different predictive factors. Moreover, a bivariate model is more helpful for inference and prediction purposes because it allows us to properly specify the dependency between the two dependent variables (see Shi & Valdez, 2014).

One way to introduce the correlation factor is to use copulas to analyse the correlation structure, by linking univariate marginals to the full multivariate distribution (see Frees & Valdez, 1998). The use of copulas is common in analysing correlation structure related to continuous variables such as claim losses (see Denuit et al., 2006; Frees & Valdez, 2008; Czado et al., 2012). In studying discrete variables such as the number of insurance claims, Cameron et al. (2004) used a bivariate copula in modelling the difference between self-reported and true doctor visits, but the application is limited to studying the distribution of the difference between two counts. Shi & Valdez (2014) considered three types of automobile claim counts using a mixture of copulas and the family of elliptical copulas. A review of using couplas to specify correlation structure can be found in a recent study by Chen & Hanson (2017).

Another group of studies analyse the correlation structure through the trivariate reduction method, where the pair of dependent variables are specified using three random variables. For example, by setting Y ₁=X ₁+X ₁₂ and Y ₂=X ₂+X ₁₂, where X ₁, X ₂ and X ₁₂ are independent Poisson random variables, Y ₁ and Y ₂ have a bivariate Poisson distribution with a covariance term derived from the use of the common Poisson variable X ₁₂ (see Kocherlakota & Kocherlakota, 1992; Johnson et al., 1997). The trivariate reduction method has been explored in Jung & Winkelmann (1993), King (1989) and Kocherlakota & Kocherlakota (2001). Karlis & Xekalaki (2005) proposed an extension to allow for a combination of common random variables. Bermúdez & Karlis (2011) postulated a zero-inflated multivariate Poisson model to account for excess of zeros in automobiles insurance claim data. In another context of frequency modelling, a multivariate Poisson-lognormal regression model has been used for prediction of crash counts (Ma et al., 2008; El-Basyouny & Sayed, 2009).

Although the trivariate reduction model can be extended to capture over-dispersion in the data, one drawback is that the correlation can only be positive (see Famoye, 2010 b ; Shi & Valdez, 2014). One way to address the issue is to use an imposed parameter in the bivariate probability function to specify a covariance term to account for correlation. As the value of this correlation parameter can be negative, zero and positive, the limitation of positive correlation is removed. Thus, the model is obviously more flexible with a more straightforward covariance structure. Lakshminarayana et al. (1999) defined a BPR model by including a multiplicative factor to capture the correlation between the two response variables. The probability function for the bivariate distribution is composed of two univariate Poisson probability functions, linked by the multiplicative correlation factor whose value depends on the embedded correlation parameter.

Based on a similar correlation structure, Famoye (2010 b ) applied a BNBR model to analyse the bivariate distribution of two series of count data, while addressing over-dispersion in the sample. The study models marginal means of the two response variables with a set of explanatory covariates in a log-linear relationship. Data from the 1977–1978 Australian health survey is used to illustrate the model and the coefficients are estimated with maximum likelihood technique. The test results show that the BNBR model provides a better fit to the data than the BPR model, and supports the use of BNBR when the variance of the data is very different from the mean. However, the correlation parameter is not significant, thus two UNBR models may be able to provide similar results in his study.

2.1. Shrinkage methods

One drawback of the likelihood-based estimation of the regression models described above in the analysis of count data is that it commonly leads to a large number of variables being used. Although it is very tempting to incorporate as much information as possible to account for the heterogeneity in the population, this strategy is more time consuming in terms of model estimation. Too many explanatory variables in a regression model can also result in overfitting and consequently poor out-of-sample predictions.

The Lasso and ridge regression are two popular methods to shrink models (see Tibshirani, 1996; James et al., 2013). Model shrinkage refers to the process of determining a smaller subset of variables that provide stronger explanatory power. Both techniques constrain the coefficient estimates through a penalty term in the maximum likelihood estimation algorithm, comprised of the coefficient values and a shrinkage parameter ω. The higher the shrinkage parameter, the higher the impact of the shrinkage penalty. As a result, the coefficient values will approach zero as ω increases without bound. The optimal ω is commonly selected using cross-validation.

The two techniques differ in the way coefficient values are incorporated in the shrinkage penalty. The Lasso uses the sum of absolute values of coefficients, and ridge regression uses the sum of squared values. Ridge regression tends to shrink all coefficients towards zero, but will not generally set any of them to exactly zero. The Lasso is an alternative to ridge regression and can force some of the coefficient estimate to exactly zero if ω is sufficiently large. In other words, Lasso performs variable selection (see James et al., 2013: Chapter 6).

The importance of model shrinkage has been recognised in the actuarial literature. First proposed by Tibshirani (1996), the Lasso has been extended to GLMs to handle count data (see Park & Hastie, 2007). Tang et al. (2014) applied adaptive Lasso to car insurance data. The risk factor selection improves the model goodness-of-fit both in the Poisson model as well as zero-inflated Poisson model. Wang et al. (2015) considered over-dispersed data and added a Lasso penalty to the maximum likelihood function of the negative binomial regression model. Their study concludes that a parsimonious model offers better prediction and interpretation. Both Tang et al. (2014) and Wang et al. (2015) used univariate regression models and applied the shrinkage technique to only one response variable. Ridge regression is shown to improve mean square error in an early study by Hoerl & Kennard (1970). The technique is then applied to many areas of science. Some examples are Shen et al. (2013), Douak et al. (2013) and Meijer & Goeman (2013).

The two shrinkage methods can be applied to regression models to remove less significant variables. As a consequence, the unnecessary complexity in the model can be reduced and this leads to easier interpretation and potentially improved out-of-sample predicition (see James et al., 2013: Chapter 6). It is these possibilities which we explore in the context of bivariate insurance claim data in this paper.

3. Methodology

3.1. BNBR model

The bivariate Poisson distribution proposed in Lakshminarayana et al. (1999) has a probability function as the product of Poisson marginals with a multiplicative factor:

(1) $$P\left( {y_{1} ,y_{2} } \right)\,{\equals}\prod\limits_{t\,{\equals}\,1}^2 {{\theta _{t}^{{y_{t} }} e^{{{\minus}\theta _{t} }} } \over {y_{t} \,!\,}}{\times}\left[ {1{\plus}\lambda \left( {e^{{{\minus}y_{1} }} {\minus}e^{{{\minus}d\theta _{1} }} } \right)\left( {e^{{{\minus}y_{2} }} {\minus}e^{{{\minus}d\theta _{2} }} } \right)} \right],\,y_{1} ,y_{2} \,{\equals}\,0,1,2,\,\ldots\,$$

where d=1−e ⁻¹. θ _t is the mean of Y _t (t=1, 2), and Y ₁ and Y ₂ are both Poisson distributed. The covariance between Y ₁ and Y ₂ is $$\lambda \theta _{1} \theta _{2} d^{2} e^{{{\minus}d\left( {\theta _{1} {\plus}\theta _{2} } \right)}} $$ and the correlation is $$\rho \,{\equals}\,\lambda \sqrt {\theta _{1} \theta _{2} } d^{2} e^{{{\minus}d\left( {\theta _{1} {\plus}\theta _{2} } \right)}} $$ . Depending on the value of λ, the two response variables Y ₁ and Y ₂ can be positively or negatively correlated, or independent if λ is equal to zero.

By using a similar approach, Famoye (2010 b ) defined a bivariate negative binomial distribution. Following the same covariance specification as Lakshminarayana et al. (1999), a bivariate negative binomial distribution has the following probability function:

(2) $$P\left( {y_{1} ,y_{2} } \right)\,{\equals}\prod\limits_{t{\equals}1}^2 \left( {\matrix{ {y_{t} {\plus}m_{t}^{{{\minus}1}} {\minus}1} \cr {y_{t} } \cr } } \right)\theta ^{{y_{t} }} \left( {1{\minus}\theta } \right)^{{m_{t}^{{{\minus}1}} }} {\times}\left[ {1{\plus}\lambda \left( {e^{{{\minus}y_{1} }} {\minus}c_{1} } \right)\left( {e^{{{\minus}y_{2} }} {\minus}c_{2} } \right)} \right],\,y_{1} ,y_{2} \,{\equals}\,0,1,2,\,\ldots\,$$

Both Y ₁ and Y ₂ are random variables and follow a negative binomial distribution, with dispersion parameters $$m_{1}^{{{\minus}1}} $$ and $$m_{2}^{{{\minus}1}} $$ , respectively. The mean of Y _t (t=1, 2) is $$\mu _{t} \,{\equals}\,m_{t}^{{{\minus}1}} \theta _{t} /\left( {1{\minus}\theta _{t} } \right)$$ and the variance is $$\sigma _{t}^{2} \,{\equals}\,m_{t}^{{{\minus}1}} \theta _{t} /\left( {1{\minus}\theta _{t} } \right)^{2} $$ . Also, $$c_{t} \,{\equals}\,E\left( {e^{{Y_{t} }} } \right)\,{\equals}\,\left[ {\left( {1{\minus}\theta _{t} } \right)/\left( {1{\minus}\theta _{t} e^{{{\minus}1}} } \right)} \right]^{{m_{t}^{{{\minus}1}} }} $$ .

Let n denote the sample size and Y _it (t=1, 2; i=1, 2, … , n) denote the count response variable, the corresponding vector of k explanatory variables is represented as x _i =(x _i0=1, x _i1, … , x _ik ). Assuming a log-linear model and the same set of covariates as possible explanatory variables for both Y _i1 and Y _i2, the means of the two response variables can be modelled as

(3) $$E\left( {Y_{{it}} \left| {x_{i} } \right.} \right)\,{\equals}\,\mu _{{it}} \,{\equals}\,{\rm exp}\left( {x_{i} \beta _{t} } \right),\,t\,{\equals}\,1,2$$

where $$\beta _{t}^{T} \,{\equals}\,\left( {\beta _{{t0}} ,\,\beta _{{t1}} ,\,\beta _{{t2}} ,\,\ldots {\!}{\!},\,\beta _{{tk}} } \right)$$ and is the vector of the coefficients estimated using the maximum likelihood method. Given that $$\theta _{{it}} \,{\equals}\,\mu _{{it}} /\left( {m_{t}^{{{\minus}1}} {\plus}\mu _{{it}} } \right)$$ , equation (2) can be rewritten as:

(4) $${ P\left( {y_{{i1}} ,y_{{i2}} } \right)\,{\equals}\, \prod\limits_{t{\equals}1}^2 \left( {\matrix{ {y_{{it}} {\plus}m_{t}^{{{\minus}1}} {\minus}1} \cr {y_{{it}} } \cr } } \right)\left( {{{\mu _{{it}} } \over {m_{t}^{{{\minus}1}} {\plus}\mu _{{it}} }}} \right)^{{y_{{it}} }} \left( {{{m_{t}^{{{\minus}1}} } \over {m_{t}^{{{\minus}1}} {\plus}\mu _{{it}} }}} \right)^{{m_{t}^{{{\minus}1}} }} {\times}\left[ {1{\plus}\lambda \left( {e^{{{\minus}y_{{i1}} }} {\minus}c_{1} } \right)\left( {e^{{{\minus}y_{{i2}} }} {\minus}c_{2} } \right)} \right] $$

Accordingly, the log-likelihood function, which is set to a maximum to estimate the model parameters, for the unshrunken model is:

(5) $$\eqalignno{ {\rm log}\,L\,{\equals}\, & \mathop {\sum}\limits_{i\,{\equals}\,1}^n \left\{ {\mathop{\sum}\limits_{t\,{\equals}\,1}^2 \left[ {y_{{it}} \,{\rm log}\,\mu _{{it}} {\minus}m_{t}^{{{\minus}1}} {\rm log}\,m_{t} {\minus}\left( {y_{{it}} {\plus}m_{t}^{{{\minus}1}} } \right)log\left( {\mu _{{it}} {\plus}m_{t}^{{{\minus}1}} } \right){\minus}{\rm log}\left( {y_{{it}} \,!\,} \right)} \right.} \right. \cr & \left. {\left. { {\plus}\mathop{\sum}\limits_{j\,{\equals}\,1}^{y_{{it}} {\minus}1} {\rm log}\left( {m_{t}^{{{\minus}1}} {\plus}j} \right)} \right]{\plus}{\rm log}\left[ {1{\plus}\lambda \left( {e^{{{\minus}y_{{i1}} }} {\minus}c_{1} } \right)\left( {e^{{{\minus}y_{{i2}} }} {\minus}c_{2} } \right)} \right]} \right\} $$

where $$c_{t} {\equals}\left( {1{\plus}d\mu _{{it}} m_{t} } \right)^{{{\minus}1/m_{t} }} $$ with d=1−e ⁻¹. Equation (5) can be maximised with respect to β _t , m _t and λ. The asymptotic standard deviations of the estimated parameters are obtained in the usual way from Hessian matrix.

The deviance for the BNBR model, which is a measure of the model’s goodness-of-fit, is defined as:

(6) $$\eqalignno{ D\,{\equals}\, & 2\mathop{\sum}\limits_{i\,{\equals}\,1}^n \left\{ {\mathop{\sum}\limits_{t\,{\equals}\,1}^2 \left[ {y_{{it}} \,{\rm log}\left( {{{y_{{it}} \left( {m_{t}^{{{\minus}1}} {\plus}\hat{\mu }_{{it}} } \right)} \over {\hat{\mu }_{{it}} \left( {m_{t}^{{{\minus}1}} {\plus}y_{{it}} } \right)}}} \right){\plus}m_{t}^{{{\minus}1}} \,{\rm log}\left( {{{m_{t}^{{{\minus}1}} {\plus}\hat{\mu }_{{it}} } \over {m_{t}^{{{\minus}1}} {\plus}y_{{it}} }}} \right)} \right]} \right. \cr & \left. { {\rm log}\left( {{{1{\plus}\lambda \prod\nolimits_{t\,{\equals}\,1}^2 {\left( {e^{{{\minus}y_{{it}} }} {\minus}\bar{c}_{t} } \right)} } \over {1{\plus}\lambda \prod\nolimits_{t\,{\equals}\,1}^2 {\left( {e^{{{\minus}y_{{it}} }} {\minus}\hat{c}_{t} } \right)} }}} \right)} \right\} $$

where $$\bar{c}_{t} $$ and $$\hat{c}_{t} $$ are the values of c _t evaluated at μ _it =y _it and $$\mu _{{it}} {\equals}\hat{\mu }_{{it}} $$ , respectively, and $$\hat{\mu }_{{it}} $$ the predicted value of μ _it found using equation (3) with estimated coefficients that maximise equation (5).

3.2. The Lasso and ridge regression

Given the BNBR model in equation (4), the coefficient vector β _t can be estimated by maximising equation (5). The resulting model will be called the full model in what follows. Here β _t (t=1, 2) are vectors each having k+1 values. These relate to the model intercept and k explanatory variable coefficients. When k is large, the model may produce poor out-of-sample results because of an overfitting problem. It is therefore useful to shrink the estimated BNBR model using either the Lasso approach or ridge regression, by subtracting a shrinkage penalty from the log-likelihood function.

We define the log-likelihood function of the BNBR model in section 3.1, which is Log L in equation (5). The new functions to be maximised under the two shrinkage approaches, with 2 × k coefficients to be analysed are specified as:

(7) $$\matrix{ {{\rm The}\,{\rm Lasso\,\colon\,}} \hfill & {{\rm log}\,L{\minus}\omega \mathop{\sum}\limits_{t\,{\equals}\,1}^2 \mathop{\sum}\limits_{j\,{\equals}\,1}^k \left| {\beta _{{tj}} } \right|} \hfill \cr {{\rm Ridge}\,{\rm regression\,\colon\,}} \hfill & {{\rm log}\,L{\minus}\omega \mathop{\sum}\limits_{t\,{\equals}\,1}^2 \mathop{\sum}\limits_{j\,{\equals}\,1}^k \beta _{{tj}}^{2} } \hfill \cr } $$

where ω is the shrinkage parameter. Here t takes values 1 and 2, indicating that the shrinkage models consider regression coefficients for both y ₁ and y ₂. Thus the above equations specify the two shrinkage models in the context of a bivariate model.

Note that we do not shrink the intercept coefficients (β _t0), as they simply constitute a measure of the mean value of the response variables when other explanatory variables are set to zero. Similarly, we also exclude the two over-dispersion parameters (m ₁, m ₂) and the correlation parameter (λ) from shrinkage, as we are focussing on shrinking the estimated association of each explanatory variable with the response. As a result, for each response variable, k regression coefficients are included in the shrinkage penalty.

When ω is equal to zero, both the Lasso and ridge regression will generate the same coefficients as the full model. A larger ω gives greater emphasis to model simplicity compared with in-sample goodness-of-fit. Consequently coefficient values will deviate from the maximum likelihood estimates, resulting in reduced in-sample goodness-of-fit. At the same time, the model is simplified with the potential for improved out-of-sample performance.

It is clear that different ω values will lead to different coefficients in the shrunken model and therefore differing out-of-sample prediction results. In order to perform the two shrinkage techniques as specified in equation (7) using the maximum likelihood method, the optimal value must be chosen for ω based on only the sample data to achieve the possibly best out-of-sample prediction accuracy. In this study we use k-fold cross-validation for this purpose, where commonly k is set to be 5 or 10. In the cross-validation process, the sample data are randomly divided into k groups. One group is chosen as the validation set, while the model is fitted on the remaining k−1 groups. The fitted model is applied to the validation set to calculate the out-of-sample deviance, as the validation set is held out in the model fitting process. As there are k groups, the procedure can be repeated k times resulting in k deviances when each of the k groups is held out as the validation set. The average of the k deviance values, each denoted deviance _i (i=1, 2, … , k), is taken as the cross-validation result, or k-fold cross-validation, at a particular ω value:

$$CV_{{(\omega )}} \,{\equals}\,{1 \over k}\mathop{\sum}\limits_{i\,{\equals}\,1}^k {\rm deviance}_{i} $$

For each of the ω values, we perform the procedure as described previously. Among a grid of ω values, the most appropriate ω is the one that generates the lowest k-fold CV. As the CVs are calculated on the validation set, separated from the data to fit the model, when ω increases the CV is expected to decrease initially and later increase again when the impact from the penalty term is too strong. The ω that gives the minimum CV should be chosen.

We note here that although we develop different log-likelihood functions and shrinkage functions for the bivariate model, the validation process is standard. This is because the validation process only takes into consideration the deviances generate by a model, whether it is univariate or bivariate. Given the specified shrinkage models in equation (5), the validation process mentioned previously is proper for the BNBR model.

The shrinkage parameter, ω, is not assumed to be the same for the two shrinkage methods. A separate cross-validation is performed for each of the methods to locate the best ω value. Once this is achieved, the model is fitted again to the full set of data, disregarding the previously k group classifications. The shrunken models can then be compared with the full model, which is estimated using maximum likelihood without any penalty term.

4. Data

The study is based on data from 14,000 automobile policies from a major insurance company in Spain, randomly selected from a pool of 80,994 policies. A subset of the data is also used in Brouhns et al. (2003), Bolancé et al. (2008), Bolancé et al. (2003), Boucher & Denuit (2008), Boucher et al. (2007), Bermúdez & Karlis (2011) and Boucher et al. (2009). We use 10,000 policies to estimate the model parameters, and the remaining 4,000 policies are used to test the model’s out-of-sample prediction accuracy.

We model two types of claims, and their associated claim counts are recorded as Y ₁ and Y ₂. Y ₁ represents the simple third-party liability with basic guarantees, and Y ₂ stands for comprehensive cover. The same set of explanatory variables are assumed to affect both Y ₁ and Y ₂. The explanatory variables are summarised in Table 1. A similar table can also be found in Boucher et al. (2009).

Table 1 Explanatory variables in the regression model.

We present in Table 2 a summary of the effects of the covariates on claim count based on all 80,994 policies ¹ . The covariates are classified into eight groups. In the first column, we present the total number of policies that fall into each subgroup, followed by the percentage of policies with claim counts equal to 0, 1 or 2 (including higher than 2) for Y ₁ and Y ₂, respectively.

Table 2 Summary statistics of claim frequencies as classified by the explanatory variables.

For example, in the case of gender, we see here 12,957 of the policyholders are female. In total, 93% of these female policyholders does not make a third-party liability claim and 91.64% does not make a claim on the comprehensive cover. This is to be compared with the male policyholders, where 93.80% of them does not make a third-party liability claim and 92.59% makes no claim on the comprehensive cover. Ignoring other covariates and factors, female policyholders tend to have a slightly riskier profile compared with male policyholders.

Similar observations can be made for the other groups of covariates. A lower claim count tends to be associated with driving in low-risk zone, a longer driving experience, a longer time with the company, an older age and a smaller car horsepower. The effects of driving area (v2) and insurance cover (v9, v10) seem to be minimal based on this one-way analysis.

The estimated mean and variance of Y ₁ and Y ₂ are given at the end of Table 2. Y ₁ has a lower mean and smaller variance compared with Y ₂. Moreover, the variance is much higher than the mean for both claim types. This feature implies that a model capable of handling over-dispersed data, such as the negative binomial regression model, is more appropriate compared with Poisson regression model.

The correlation coefficient between Y ₁ and Y ₂ is 0.187, taking into account all 80,944 observations. The scatter plot is presented in Figure 1, including a trend line. The two variables can only take integer values. The number of observations at each of the dots is relatively indicated by the size of the dot, which is a rough reflection of the exact count summary shown in Table 3.

Figure 1 Scatter plot of two insurance claim counts. The size of the dot at each point gives a relative indication of the number of observations. The trend line is also presented.

Table 3 Summary table of two types of insurance counts.

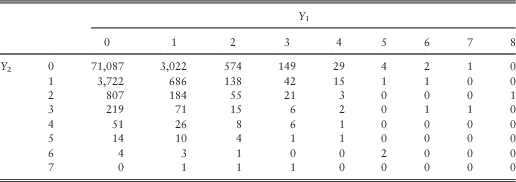
We also analyse the correlation structure in the tail, when at least one of the claim counts is not zero. The correlation coefficient is computed at 0.126, which is lower than if all observations are considered. This is consistent with the statistics in Table 3. If a higher right-tailed correlation is found, modelling tools such as copulas can be used to more accurately model the correlation structure (see Denuit et al., 2006: Chapter 4.4.4). As tail dependency is not presented in this study, the model specified in equation (2) will suffice.

In addition to the variables listed in previous tables, we also consider two-way interaction effects among the variables. Adding interaction terms between independent covariates help relax the assumption that each of those independent variables only has additive effect in the regression model (see Fahrmeir et al., 2013). Interaction effects are frequently analysed in regression models and have been considered in claim counts models (see Yip & Yau, 2005; Shi & Valdez, 2014). We have initially considered 14 potential two-way interactions. These terms cover the interaction effects between different groups of covariates, for example, gender and driving experience, and are summarised in Table 4. We note that after model shrinkage many of the interaction terms were removed from the model.

Table 4 Interaction terms used in the regression model.

The total number of variables we use in the regression model is 25, excluding the intercept. Although we use the same set of variables for both response variables, we do not expect all explanatory variables to be significant in evaluating the claim counts, nor that the coefficients are the same for Y ₁ and Y ₂.

5. Results

5.1. BNBR model

We present in Table 5 the results of fitting four models: the BNBR model, UNBR model for Y ₁, UNBR model for Y ₂, and the BPR model. The four models are classified as full models as opposed to shrunken models, since at this stage we use all available variables including the chosen interaction terms. The BNBR model is specified in equation (4). The two UNBR models are fitted separately for each of the two response variables. The BPR model specification is the same as in Lakshminarayana et al. (1999) and is given in equation (1).

Table 5 Modelling results of the BNBR model, two UNBR models and the BPR model, which are all classified as the full models.

Note: The coefficients of each variable are shown, followed by their standard deviation in parentheses.

BNBR, bivariate negative binomial regression; UNBR, univariate negative binomial regression; BPR, bivariate Poisson regression.

*,**,*** represent, respectively, statistical significance at the 10%, 5% and 1% level, calculated based on the t-statistics of coefficients of each variable.

The results from the BNBR model are compared with the UNBR models. Coefficients from the BNBR model are consistent with those in UNBR models, both in terms of sign and statistical significance. By introducing a correlation factor λ, which is significant at the 1% level in the BNBR model, it is observed that the deviance of BNBR model is much lower than the sum of the deviances of the two UNBR models. It is true both in sample and out of sample, implying that the BNBR model provides a better in-sample goodness-of-fit, as well as more accurate out-of-sample prediction. It adds value to analyse the two correlated variables in a bivariate model, to properly account for the dependence between the two types of claim counts.

Consistent with expectation, the BNBR model also outperforms the BPR model. Although the BPR model recognises the correlation between the two response variables, the BNBR is more appropriate here when the data are over-dispersed and the variance of the claim counts is much higher than the mean for both types of claims as shown in Table 2. For this reason the BNBR generates both lower in-sample and out-of-sample deviances as expected.

5.2. The Lasso and ridge regression

The first step when applying the two shrinkage techniques is to choose the most optimal shrinkage parameter ω through cross-validation. We choose k=10 and use tenfold cross-validation which is widely used and effective, see for example, Kohavi (1995) ² . The two intercept coefficients (β ₁₀ and β ₂₀), the dispersion parameters (m ₁ and m ₂) and the correlation parameter (λ) are excluded from the shrinkage process. For each of the two dependent variables, Y ₁ and Y ₂, 25 coefficients are estimated by maximising the penalised log-likelihood in equation (7).

We select a grid of values for ω ranging from 0 to 50, and perform the procedure as described in section 3.2. The sample data containing 10,000 policyholders is randomly divided into ten groups. One group is held out as the validation group while the model is fitted on the other nine groups at various ω values. This results in a number of different shrunken models and accordingly different deviance values based on equation (6) calculated on the validation set. Repeated ten times for ten different validation sets, we reach a series of CV _(a) computed as the average of deviances from the ten validation sets at a, where a denotes different ω values from 0 to 50.

We present in Figure 2 the CV _(a) values from the cross-validation process. As expected, CV _(a) decreases initially to a minimum before increasing again. When ω is zero, the shrunken models are equivalent to the full model. When ω increases, the deviances calculated using the held-out group first decrease, indicating better out-of-sample prediction results. Both of the curves increase again after reaching a minimum, where the shrinkage penalty is too strong and affects the models’ prediction power.

Figure 2 Deviances from cross-validation at different ω values. Each deviance in the graph is calculated as the average of the ten deviances at the same ω generated in the tenfold cross-validation process.

The shrinkage parameter, ω, in the Lasso and ridge regression are chosen using the cross-validation procedure. We get distinct optimal ω values that minimise deviance under the two different methods. As can be seen in Figure 2, the optimal ω chosen for the Lasso was found to be around 13, and the optimal ω for ridge regression was found to be around 4. We refit the BNBR model under two shrinkage approaches at given ω using the penalised log-likelihood as specified in equation (7). The estimated coefficients as well as the chosen ω are all presented in Table 6. The full BNBR model fitted previously in section 5.1 is also included.

Table 6 Modelling result for the original full bivariate negative binomial regression model and shrunken models.

Note: The coefficients of each variable are shown, followed by their standard deviation in parentheses.

*,**,*** represent, respectively, statistical significance at the 10%, 5% and 1% level, calculated based on the t-statistics of coefficients of each variable.

Two observations from Table 6 can be made. First, the full model provides the best in-sample goodness-of-fit among the three, indicated by its lowest in-sample deviance. This is as expected as the full model is estimated to fit the sample data as closely as possible. Second, both shrunken models outperform the full model in out-of-sample prediction accuracy. The Lasso-shrunken model is the best among the three, with an out-of-sample deviance of 2,586.82, <2,626.77 of the shrunken model obtained using ridge regression.

The shrinkage effect is more obvious in the Lasso-shrunken model. Many of the coefficients are forced to zero, including the insignificant ones identified in the full model. This indicates that those variables are not important in assessing the claim counts, and once removed, the out-of-sample prediction of the model is greatly improved. One possible explanation is that the full model overfits the sample data and thus underperforms shrunken models in making predictions. With fewer explanatory variables, the shrunken model is also much easier to interpret.

The shrinkage effect is not as obvious in the model regularised by ridge regression and none of the coefficients is zero after the shrinkage process. However, many coefficient values are more close to zero than in the full model, while the more significant variables, such the intercept, have a higher absolute coefficient and are still significant. This may explain why the shrunken model also outperforms the full model even when it uses a similar set of variables. Some coefficients of the regression may be reduced as ridge regression can be applied to treat the problem of collinearity between independent variables (see García et al., 2015). In this study, we use categorical variables with values of 0 or 1, which may still lead to some potential for collinearity, for example, between the policyholder’s age and driving experience measured in years. As a result, treating the problem of collinearity may further improve the out-of-sample prediction accuracy.

The different results from the Lasso and ridge regression can also be explained with reference to Figure 3, which is similar to that in James et al. (2013: Chapter 6, 222). The graph on the left refers to a two-dimensional coefficient scope of the Lasso, and the graph on the right represents the ridge regression. In both graphs, the dot inside the ellipses indicates the maximum likelihood estimator $$\hat{\beta }$$ without any shrinkage penalty. Assuming the same constraint amount s is used in both methods, this means |β ₁|+|β ₂|≤s and $$\beta _{1}^{2} {\plus}\beta _{2}^{2} \leq s$$ , which can be represented by the grey area. If s is large enough to reach $$\hat{\beta }$$ , the Lasso and ridge regression estimates will be the same as the maximum likelihood estimates (e.g. when ω=0).

Figure 3 Comparison of the least absolute shrinkage and selection operator (Lasso) (left) and ridge regression (right).

The ellipses around $$\hat{\beta }$$ represent regions of constant log-likelihood. The ellipses will expand away from $$\hat{\beta }$$ and touch the grey constraint area to satisfy the imposed shrinkage penalty. During this process, the Lasso is very likely to end up on one axis while ridge regression will land on the sphere, both shown in the graph as the cross. As a result, in the Lasso selection coefficients are commonly set to zero, while the same cannot be said for ridge regression. This simple graphical example can be extended to the higher dimensional case, when many Lasso estimated coefficients are equal to zero simultaneously.

To support the discussion and to show how the coefficient values react under the two shrinkage techniques, we present the shrunken coefficients at different ω values from the cross-validation procedure, computed as the average value across the ten different models, each fitted when one group is held as the validation set. Note that we only plot the coefficients of explanatory variables, which are directly reduced in the shrinkage process. Figures 4 and 5 show the results from the Lasso and ridge regression, respectively, and present how the 25 coefficients change when the shrinkage parameter increases from 0 to 50 for Y ₁ and Y ₂ in separate graphes. As expected, all coefficients decrease with an increasing shrinkage parameter. They behave differently for Y ₁ and Y ₂, with some persistent coefficients significantly different from zero even at large ω values. These are specifically labelled on the figures.

Figure 4 Shrunken coefficients: the least absolute shrinkage and selection operator (Lasso).

Figure 5 Shrunken coefficients: ridge regression.

However, it is quite noticeable that when ω is very large (i.e. set to 50), the coefficients in Figure 4 for the Lasso are much closer to zero, compared with those found in ridge regression in Figure 5. In particular, it can be observed that although the coefficients in Figure 5 approach zero initially and a few of them eventually become very close to zero in the end, most coefficients keep a constant distance away from zero which lasts to the end. The findings confirm the discussion made previously, that the two shrinkage techniques affect the coefficients in much distinctive ways.

The two shrinkage techniques are also applied to UNBR models in a similar way. For each response variable, two shrunken models are generated at given ω values selected by cross-validations. The results are presented in Table 7. Two full UNBR models estimated previously are also presented here.

Table 7 Modelling results of the original full univariate negative binomial regression (UNBR) model and UNBR models shrunken by the two methods.

Note: The coefficients of each variable are shown, followed by their standard deviation in parentheses.

*,**,*** represent, respectively, statistical significance at the 10%, 5% and 1% level, calculated based on the t-statistics of coefficients of each variable.

Similar conclusions can be drawn from the shrunken UNBR models. For Y ₁, both of the two shrunken models outperform the full model in out-of-sample prediction, implied by lower deviances. For Y ₂, although the full model provides the best in-sample goodness-of-fit, it underperforms the shrunken models out-of-sample, with a lower log-likelihood and higher deviance.

By comparing the results for the Lasso-shrunken BNBR model in Table 6 and the two Lasso-shrunken UNBR models in Table 7, we see that the in-sample deviance of the BNBR model is much lower than the deviances from the two UNBR models combined, implying a better in-sample goodness-of-fit. The out-of-sample deviances are similar for the BNBR model and UNBR models. Obtained using ridge regression, the shrunken BNBR model outperforms the two shrunken UNBR models, providing both lower in-sample and out-of-sample deviances. This is in consistent with the conclusion we draw from the full models. It is beneficial to analyse the two response variables together in a bivariate model and properly account for the correlation structure between them.

6. Conclusion

In this paper we use the BNBR model to analyse general insurance claim data. We show that with a more flexibly specified correlation structure, the BNBR model adequately captures the relationship between the two claim counts and the set of explanatory variables. The correlation, which is totally ignored if two UNBR are fitted separately, proves to be essential in analysing the two types of claim counts from the same policyholder. Note that the correlation coefficient between the two claim count is only 0.187 in this study which is considered as a weak correlation. When a higher correlation coefficient is present, it is likely that a bivariate model with a proper specification of the correlation structure is more suitable than a univariate model.

In addition, we apply two shrinkage techniques to choose core independent variables in modelling claim counts. The results from the Lasso and ridge regression are different, but both shrunken models outperform original full regression models which are likely to suffer from the overfitting problem. The shrunken models provide much better out-of-sample prediction accuracy in both UNBR and BNBR models. This automatic approach to model selection has considerable potential for application in actuarial modelling where very large numbers of variables and data points are often available. Moreover, the shrunken BNBR models also outperforms the two separately fitted shrunken UNBR models, which again emphasises the importance of properly accounting for the correlation structure between response variables.

In addition to BNBR model in this study, some extended Poisson model can also incorporate over-dispersion. For example, the zero-inflated versions of multivariate Poisson models used in Bermúdez & Karlis (2011), where the correlation structure in equation (2) can be implemented instead of the full covariance specification. The bivariate generalised Poisson regression model in Famoye (2010 a ) follows a similar correlation structure as in this study, which also allows for over-dispersion. These potential alternative models can be considered in future research.