Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T07:33:51.321Z Has data issue: false hasContentIssue false
  • English
  • Français

A family of protein growth curves with extension to other chemical body components together with application to animal nutrition and improvement

Published online by Cambridge University Press:  05 October 2010

C. Z. Roux
C. Z. Roux*
Affiliation:
Department of Genetics, University of Pretoria, Pretoria 0002, Republic of South Africa
*
†E-mail: [email protected]
Get access

Abstract

Theory that successfully explains the magnitude and range of estimates of protein retention (PR) efficiency from the cost of turnover of existing protein indicates that conventional curves for growth description are inappropriate for protein growth. A solution to this problem is found in the consideration that the rate-limiting steps for protein synthesis (PS) and breakdown are likely to be associated with the diffusion of metabolites in and between cells. The algebraic scaling of nuclear and cellular diffusion capacity with tissue or total body protein leads to a parameterization of the primal differential equation for PR (kg/day) based on two terms representing PS and breakdown, viz.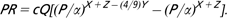where c is an arbitrary constant, Q is the proportion of nuclei active in cell growth or division in a tissue or the whole body, α is the limit mass for protein (P, kg) in a tissue or the whole body, the power X+Z represents the rate-limiting steps in protein breakdown and Y is the power of the relationship between cell volume and the amount of tissue protein. For the whole body, the contribution of the different tissues should be weighted in proportion to their PS rates with, on average, Y = 1/2. The constant 4/9 arises from the scaling of the specific diffusion rate of DNA activator precursors from nuclear dimensions and from the relationship between nuclear and cell volume. Experimental evidence on protein breakdown rate as well as protein and body mass points of inflection indicates that the range of theoretically possible numerical values of the rate-limiting powers X+Z = (i+ 3)/9 for i = 1, 2, … ,12 seems adequate for the description of the range of observed whole body protein and body mass growth patterns for mammals. Q = 1 represents maximal protein retention, and for 0 < Q < 1, experimental evidence exists in support of a theoretical relationship between Q and food ingestion. The conclusion follows that some knowledge of the protein limit mass (α) and of the point of inflection (related to X + Z) is the main requirement for the application of the theory for description and prediction in animal nutrition and breeding.

Keywords

protein growth curvesintake predictionanimal improvement
Type
Full Paper
Information
animal , Volume 5 , Issue 3 , March 2011 , pp. 439 - 449
Copyright
Copyright © The Animal Consortium 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agricultural Research Council (ARC) 1980. The nutrient requirements of ruminant livestock. CAB International, Wallingford, UK.Google Scholar
Agricultural Research Council 1981. The nutrient requirements of pigs. Commonwealth Agricultural Bureaux, Slough, UK.Google Scholar
Bates, PC, Millward, DJ 1981. Characteristics of skeletal muscle growth and protein turnover in a fast-growing rat strain. British Journal of Nutrition 46, 7–13.CrossRefGoogle Scholar
Darnell, JE, Lodish, HF, Baltimore, D 1990. Molecular cell biology, 2nd edition. Scientific American Books Inc., New York, USA.Google Scholar
Di Marco, ON, Baldwin, RL, Calvert, CC 1989. Simulation of DNA, protein and fat accretion in growing steers. Agricultural Systems 29, 21–34.CrossRefGoogle Scholar
Doornenbal, H 1971. Growth, development and chemical composition of the pig. 1. Lean tissue and protein. Growth 35, 281–295.Google Scholar
Enesco, M, Leblond, CP 1962. Increase in cell number as a factor in the growth of the organs and tissues of the young male rat. Journal of Embryology and Experimental Morphology 10, 530–562.Google Scholar
Fauconneau, B, Arnal, M 1985. In vivo protein synthesis in different tissues and the whole body of rainbow trout (Salmo Gairdnerii R.): influence of environmental temperature. Comparative Biochemistry and Physiology Part A: Comparative Physiology 82, 179–187.CrossRefGoogle ScholarPubMed
Gaillard, J-M, Pontier, D, Allaine, D, Loison, A, Herve, J-M, Heizmann, A 1997. Variation in growth form and precocity at birth in eutherian mammals. Proceedings of the Royal Society of London: Series B 264, 859–868.Google Scholar
Goldspink, DF, Kelly, FJ 1984. Protein turn-over and growth in the whole body, liver and kidney of the rat from the foetus to senility. Journal of Biochemistry 217, 507–516.CrossRefGoogle Scholar
Kang, CW, Sunde, ML, Swick, RW 1985a. Growth and protein turnover in the skeletal muscle of broiler chicks. Poultry Science 64, 370–379.Google Scholar
Kang, CW, Sunde, ML, Swick, RW 1985b. Characteristics of growth and protein turnover in skeletal muscle of turkey poults. Poultry Science 64, 380–387.Google Scholar
Knap, PW 2000. Time trends of Gompertz growth parameters in ‘meat-type’ pigs. Animal Science 70, 39–49.CrossRefGoogle Scholar
Kyriazakis, I, Emmans, GC 1992. The effects of varying protein and energy intakes on the growth and body composition of pigs. 2. The effects of varying both energy and protein intake. British Journal of Nutrition 68, 615–625.CrossRefGoogle ScholarPubMed
Latchman, DS 2005. Gene regulation, 5th edition. Taylor and Francis, Abingdon, UK.Google Scholar
Marumatsu, T, Okumura, J-I 1985. Whole body protein turnover in chicks at early stages of growth. Journal of Nutrition 115, 483–490.Google Scholar
Millward, DJ, Garlick, PJ, Steward, RJC, Nnanyelugo, DO, Waterlow, JC 1975. Skeletal-muscle growth and protein turnover. Biochemical Journal 150, 235–243.Google Scholar
Moughan, PJ 1999. Protein metabolism in the growing pig. In A quantitative biology of the pig (ed. I Kyriazakis), pp. 299–331. CABI Publishing, Wallingford, UK.Google Scholar
Noblet, J, Karege, C, Dubois, S 1994. Prise en compte de la variabilité de la composition corporelle pour la prévision du besoin énergétique et de l’efficacité alimentaire chez le porc en croissance. Journées de la Recherche Porcine en France 26, 267–276.Google Scholar
Oltjen, JW, Bywater, AL, Baldwin, RL 1985. Simulation of normal protein accretion in rats. Journal of Nutrition 115, 45–52.CrossRefGoogle ScholarPubMed
Quiniou, N, Dourmad, J-Y, Noblet, J 1996. Effect of energy intake on the performance of different types of pig from 45 to 100 kg body weight. 1. Protein and lipid deposition. Animal Science 63, 277–288.Google Scholar
Quiniou, N, Noblet, J 1995. Prediction of tissular body composition from protein and lipid deposition in growing pigs. Journal of Animal Science 73, 1567–1575.CrossRefGoogle Scholar
Reeds, PJ, Cadenhead, A, Fuller, MF, Lobley, GE, McDonald, JD 1980. Protein turnover in growing pigs. Effects of age and food intake. British Journal of Nutrition 43, 445–455.CrossRefGoogle ScholarPubMed
Reiss, MJ 1989. The allometry of growth and reproduction. Cambridge University Press, Cambridge, UK.CrossRefGoogle Scholar
Richards, FJ 1959. A flexible growth function for empirical use. Journal of Experimental Botany 10, 290–300.CrossRefGoogle Scholar
Roux, CZ 2005a. Incorporating turnover in whole body protein retention efficiency in pigs. Animal Science 80, 71–81.CrossRefGoogle Scholar
Roux, CZ 2005b. Incorporating turnover in whole body protein retention efficiency in cattle and sheep. Animal Science 80, 345–351.CrossRefGoogle Scholar
Roux, CZ 2006. Incorporating turnover in estimates of protein retention efficiency for different body tissues. British Journal of Nutrition 95, 246–254.Google Scholar
Roux, CZ 2010. A family of protein growth curves with extension to other chemical body components together with application to animal nutrition and improvement. Animal (online appendix – www.journals.cambridge.org/anm)Google Scholar
Sandberg, FB, Emmans, GC, Kyriazakis, I 2005. Partitioning of limiting protein and energy in the growing pig: testing quantitative rules against experimental data. British Journal Nutrition 93, 213–224.Google Scholar
Siebrits, FK 1984. Some aspects of chemical and physical development of lean and obese pigs during growth. DSc. (Agric) thesis, University of Pretoria, RSA.Google Scholar
Siebrits, FK, Barnes, PM 1989. The change in the rate of muscle protein metabolism of rats from weaning to 90 days of age. Comparative Biochemistry and Physiology Part A: Physiology 92, 485–488.CrossRefGoogle ScholarPubMed
Taylor, St CS 1980. Genetic size-scaling rules in animal growth. Animal Production 30, 161–165.Google Scholar
Teissier, G 1941. Sur le rapport nucléoplasmatique des cellules de mammifères. Comptes-rendus des séances de la Société de biologie et de ses filiales 135, 662–666.Google Scholar
Tullis, JB 1981. Protein growth in pigs. PhD thesis, University of Edinburgh, UK.Google Scholar
Ursin, E 1979. Principles of growth in fishes. Symposia of the Zoological Society of London 44, 63–87.Google Scholar
Van Lunen, TJA 1994. A study of the growth and nutrient requirements of highly selected pigs. PhD thesis, University of Nottingham, UK.Google Scholar
von Bertalanffy, L 1960. Principles and theory of growth. In Fundamental aspects of normal and malignant growth (ed. WW Nowinski), pp. 137–259. Elsevier, Amsterdam, The Netherlands.Google Scholar
Waterlow, JC 1984. Protein turnover with special reference to man. Quarterly Journal of Experimental Physiology 69, 409–438.CrossRefGoogle ScholarPubMed
Supplementary material: File

Roux supplementary material

Appendix.doc

Download Roux supplementary material(File)
File 219.1 KB