Published online by Cambridge University Press: 01 August 2014
Various attempts have been made in recent years to analyze judicial decisions in selected areas of law as functions of controlling facts. At least two of these attempts have relied on systems of simultaneous equations. In both endeavors the assumption was made that the combination of facts on which the decisions depend is linear. In the absence of any clear indication of a nonlinear combination, as well as in view of the significant results that were obtained on the basis of a linear model, the initial approach was justified. The use of high speed digital computers has made it possible, however, to explore the existence of nonlinear relationships where the original assumption of linear relationships was made. The important feature in detecting nonlinear relationships is not primarily the greater accuracy of the results—the linear model has provided acceptable approximations—but the acquisition of new insights into how different facts combine in influencing judicial decisions.
It is the purpose of this paper first to review the linear model, and then to show how it can be extended to a nonlinear model—in general terms as well as in the form of an actual application. Finally, limitations and implications of the nonlinear model will be indicated.
Support for this research was provided by a grant awarded by the Committee on Governmental and Legal Processes of the Social Science Research Council. The IBM 7040, which was supported in part by Grant GF-1819 of the National Science Foundation, and the IBM 360 at the Computer Center of the University of Connecticut have been used extensively throughout the entire research. The assistance which has been received from the research foundations and from the University is gratefully acknowledged.
1 Kort, Fred, “Simultaneous Equations and Boolean Algebra in the Analysis of Judicial Decisions,” Law and Contemporary Problems, 28 (Winter, 1963), 143–163 CrossRefGoogle Scholar; and “Content Analysis of Judicial Opinions and Rules of Law,” in Schubert, Glendon (ed.), Judicial Decision-Making (New York: Free Press of Glencoe, 1963), pp. 133–197 Google Scholar; Ulmer, S. Sidney, “Quantitative Analysis of Judicial Processes: Some Practical and Theoretical Applications,” Law and Contemporary Problems, 28 (Winter, 1963), 164–184 CrossRefGoogle Scholar; and “Mathematical Models for Predicting Judicial Behavior,” in Bernd, Joe (ed.), Mathematical Applications in Political Science, III (Charlottesville, Va.: University of Virginia Press, 1967).Google Scholar A different approach, employing Boolean algebra, has been used by Lawlor, Reed C.; see his “Foundations of Logical Legal Decision Making,” Modern Uses of Logic in Law (06, 1963), pp. 98–114 Google Scholar, and Kort, supra.
2 Miranda v. Arizona, 384 U. S. 436 (1966).
3 This is the method which was used in my studies cited in note 1. For a somewhat different application of multiple regression to the analysis of judicial decisions, see Gruenbaum, Werner F. and Newhouse, Albert, “Quantitative Analysis of Judicial Decisions: Some Problems of Prediction,” Houston Law Review, 3 (1965) 201–220.Google Scholar
4 This is the method which was used in the studies by Ulmer, see supra, note 1. For a somewhat different application of discriminant analysis to judicial decisions, see S. Sidney Ulmer, “The Discriminant inunction and a Theoretical Context for Its Use in Estimating the Votes of Judges,” to be published in a forthcoming volume by John Wiley and Sons, edited by Joseph Tanenhaus and Joel Grossman.
5 See Tiedeman, David V., “The Utility of the Discriminant Function in Psychological and Guidance Investigations,” Harvard Educational Review, 21 (Spring, 1951), 71–80, at 79.Google Scholar
6 This method has been used in my earlier studies and in the more recent study by Ulmer, see supra, note 1.
7 It should be noted, however, that precisely this type of function is very meaningful in the analysis of some judicial decisions in Roman law systems. In the latter, the presence of specified facts frequently is designated by legislatures or courts as a set of indispensable conditions for a decision in favor of the aggrieved party. A forthcoming study by the author, to be presented at the APSA Annual Meeting in 1968, will exemplify this point with regard to Swiss cases.
8 The significance test which can be employed here is the F test for determining significance of nonlinear regression over linear regression or higher order nonlinear regression over lower order nonlinear regression:
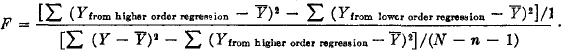
See Croxton, F. E. and Cowden, D. J., Applied General Statistics, 2nd. Ed. (Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1955), pp. 726–732 Google Scholar, including the exposition of the t-test on p. 727.
9 See, e.g., Johnson, R. E. and Kiokemeister, F. L., Calculus, 3rd. Ed. (Boston: Allyn and Bacon, Inc., 1964), pp. 397–401 Google Scholar, and Protter, M. H. and Morrey, C. B. Jr., College Calculus (Reading, Mass.: Addison-Wesley Publ. Co., Inc., 1964), pp. 695–699.Google Scholar This method was brought to the attention of the author by Professor Elliot S. Wolk, Department of Mathematics, University of Connecticut.
10 Copies of the complete set of data and results may be obtained from the author.
11
12 See Kort, Fred, “Models for the Analysis of Fact-Acceptance by Appellate Courts,” The American Behavioral Scientist, 9 (04, 1966), 8–10 CrossRefGoogle Scholar; and “Quantitative Analysis of Fact-Patterns in Cases and Their Impact on Judicial Decisions,” Harvard Law Review, 79 (June, 1966), 1595–1603.
13 See supra, note 7.
Comments
No Comments have been published for this article.