Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-30T15:34:15.217Z Has data issue: false hasContentIssue false
  • English
  • Français

An Axiomatic Model of Voting Bodies*

Published online by Cambridge University Press:  01 August 2014

Steven J. Brams  and
Michael K. O'Leary
Steven J. Brams
Affiliation:
New York University
Michael K. O'Leary
Affiliation:
Syracuse University
Get access Rights & Permissions [Opens in a new window]

Extract

The act of voting in legislative and judicial bodies is one of the most widespread and valuable sources of information available to political analysts. When individuals make structured choices within some known institutional constraints, there is opportunity for the generation of data concerning how issues are collectively defined within an institution, the relative position of each actor with regard to every other actor, and the identification of blocs of actors which are more or less persistent from one issue to another over time. With proper techniques of analysis, we should be able not only to generalize about behavior within a given voting body but also to make general statements about the voting process.

Cumulative studies of voting can be undertaken, however, only on the basis of some paradigm of the voting process—that is, some consensus on how voting as an act of political commitment is to be viewed. Such a paradigm not only should provide a viewpoint for the study of voting but should also suggest an orientation to the more general political phenomenon of which voting is an example—that is, actors making mutually exclusive choices in response to a series of questions, issues, candidates, etc. That such an agreed-upon viewpoint—not to mention a model that gives the viewpoint a precise focus—does not exist is obvious from the uses which have been made of voting data. Despite the ubiquity of such data and the many different kinds of analyses that have been performed on them, there is no model available that logically interrelates (1) systemic characteristics of voting bodies, (2) individual characteristics of their members, and (3) relational characteristics between pairs of members in such a way as to yield operational measures of voting behavior that are comparative in nature.

Type
Research Article
Information
American Political Science Review , Volume 64 , Issue 2 , June 1970 , pp. 449 - 470
Copyright
Copyright © American Political Science Association 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This is a revised version of a paper presented at the Conference on Mathematical Theory of Committees and Elections, Institute for Advanced Studies, Vienna, June 26–28, 1968; and at the Annual Meeting of the American Political Science Association, New York City, September 2–6, 1969. We wish to acknowledge the valuable research assistance offered on this paper by Alan D. Miller and the financial support of the National Science Foundation under Grant GS-2161.

References

1 We use the term “paradigm” to indicate the generally accepted assumptions, concepts, and techniques used by members working in a particular field or on a particular problem, but not necessarily accepted by, or relevant to, all members of a discipline like political science. See Kuhn, Thomas, The Structure of Scientific Revolutions (Chicago: University of Chicago Press, 1962), esp. pp. 49ff.Google Scholar

2 We use the term “model” to mean both (1) an arithmetical representation of empirical phenomena, characterized by a set of tautological or logically true statements to which we shall coordinate descriptive concepts (e.g., Agreement Level, Variance Level, etc.), and (2) a formalization achieved by replacing descriptive concepts with symbols that facilitate the deduction of theorems. For an explication of these different meanings of the term “model,” see Brodbeck, May, “Models, Meaning, and Theories,” in her Readings in the Philosophy of the Social Sciences (New York: Macmillan Company, 1968), esp. pp. 588–597Google Scholar.

3 For a useful survey of different methods that have been used to analyze roll-call data, see Anderson, Lee F., Watts, Meredith W. Jr., and Wilcox, Allen R., Legislative Roll-Call Analysis (Evanston, Ill.: Northwestern University Press, 1966)Google Scholar. See also MacRae, Duncan Jr., Issues and Parties in Legislative Voting: Methods of Statistical Analysis (New York: Harper & Row, 1970)Google Scholar for a careful and sustematic review of the statistical literature relevant to roll-call analysis.

4 As distinguished from a priori probabilities based strictly on the outcomes of a conceptual experiment. Although we shall present in the beginning an abstract model of the outcomes of a voting experiment, we wish to differentiate this kind of model, whose probabilities depend on the actual voting of members of a body, from models in which the probabilities arise from the institutional prerogatives of the members (i.e., the “voting rules” of the system). For an example of the latter kind of model, see Shapley, L. S. and Shubik, Martin, “A Method for Evaluating the Distribution of Power in a Committee System,” this Review, XLIII (1954), 787–792Google Scholar; for an example of the kind of model used in this article that is based on the distribution of different kinds of votes, see Riker, William H., “A Method for Determining the Significance of Roll Calls in Voting Bodies,” in Wahlke, John C. and Eulau, Heinz (eds.), Legislative Behavior: A Reader in Research and Theory (Glencoe, Ill.: Free Press of Glencoe, 1959), pp. 377–384Google Scholar. It should be noted that the distinction we draw between a priori and a posteriori probabilities is quite different from that made in applications of Bayes' theorem. Cf. Zehna, Peter W., Finite Probability (Boston: Allyn and Bacon, Inc., 1969), pp. 47–50Google Scholar.

5 We have chosen to develop our model in terms of three kinds of votes instead of two since abstention is a frequently chosen voting option in some bodies (e.g., UN General Assembly, whose roll calls for several sessions we are now analyzing using the indicators of the model).

6 An excellent reference is Feller, William, An Introduction to Probability Theory and Its Applications, Vol. I (3d ed. rev.; New York: John Wiley and Sons, Inc., 1968)Google Scholar; at a less advanced level, see Kemeny, John G., Snell, J. Laurie, and Thompson, Gerald L., Introduction to Finite Mathematics (Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1966), chpts. 3 and 4Google Scholar.

7 Pioneering works by economists, relevant to political science, that employ the axiomatic approach include Arrow, Kenneth J., Social Choice and Individual Values (New York: John Wiley & Sons, Inc., 1951)Google Scholar; Downs, Anthony, An Economic Theory of Democracy (New York: Harper and Brothers, 1957)Google Scholar; Black, Duncan, The Theory of Committees and Elections (Cambridge, Eng.: Cambridge University Press, 1958)Google Scholar; and Buchanan, James and Tullock, Gordon, The Calculus of Consent: Logical Foundations of Constitutional Democracy (Ann Arbor, Michigan: University of Michigan Press, 1962)CrossRefGoogle Scholar. Major works by political scientists using this general approach, though with rather different specific emphases, are Dahl, Robert A., A Preface to Democratic Theory (Chicago: University of Chicago Press, 1956)Google Scholar; Kaplan, Morton, System and Process in International Politics (New York: John Wiley & Sons, Inc., 1957)Google Scholar; and Riker, William H., The Theory of Political Coalitions (New Haven, Conn.: Yale University Press, 1962)Google Scholar.

8 See the “Symposium on Scientific Explanation in Political Science” between John G. Gunnell and Arthur S. Goldberg and A. James Gregor, this Review, LXVIII (Dec. 1969), 1233–1262.

9 For a brief history of the axiomatization of geometry, see Hochberg, Herbert, “Axiomatic Systems, Formalization, and Scientific Theories,” in Gross, Llewellyn (ed.), Symposium on Sociological Theory (New York: Harper & Row, 1959), pp. 419–422Google Scholar.

10 Similar calculations could be made for the probability that blocs of three or more members agree on a particular roll call. For example, the probability that three randomly-selected members—p, q, and r—agree on a particular roll call is

For a discussion of the probability of bloc voting under varying assumptions, see Arend Lijphart, “The Analysis of Bloc Voting in the General Assembly: A Critique and a Proposal,” this Review, LVII (12. 1963), 906–908Google Scholar.

11 The probability of paired disagreements, based on the party affiliations of members rather than their actual votes on roll calls, is what Douglas W. Rae calls the “fractionalization” of seat shares in a parliamentary body. His probability calculations are valid, however, only for a body that approaches infinite size in which, having chosen one member of the body, the probability of choosing another member of the same (or a different) party is unaltered by the fact that there is one less member of the body (and the party, if it were that made on the previous choice) from which the second choice can be made. Since we are dealing with bodies of finite size, Rae's assumption of sampling with replacement is un-tenable and we must instead assume sampling without replacement in calculating these probabilities. Fortunately, the practical difference between these two assumptions is small except when the fractionalization index is applied to small voting bodies, so most of Rae's empirical results on fractionalization probably remain unaffected by his erroneous calculations. See The Political Consequences of Electoral Laws (New Haven, Conn.: Yale University Press, 1967), pp. 62ffGoogle Scholar. We shall see later that the size of a voting body will affect the probability that two randomly-selected members agree (or disagree), which Rae did recognize in a subsequent article, “A Note on the Fractionalization of Some European Party Systems,” Comparative Political Studies, I (10. 1968), 413–418Google Scholar. For a generalization of the fractionalization index to the study of political cleavages, see Taylor, Michael and Rae, Douglas, “An Analysis of Crosscutting between Political Cleavages,” Comparative Politics, 1 (07 1969), 534–547CrossRefGoogle Scholar; and Rae and Taylor, On Political Cleavages, forthcoming. An ingenious index, Aij, developed by Duncan MacRae, Jr., for measuring agreement between two specific members of a voting body, has a probabilistic interpretation for bodies that approach infinite size in which two voting options are allowed: when two members agree, Aij, is equal to the probability of two randomly-selected members' taking the contrary position; when two members disagree, Aij is equal to one-half the negative value of the probability of two randomly-selected members' taking different positions. These curious values have substantive implications which, as S. Sidney Ulmer has shown, are not justified by any explicit theoretical framework. See MacRae, Duncan Jr., “Indices of Pairwise Agreement Between Justices or Legislators,” Midwest Journal of Political Science, X (02., 1966), 138–141CrossRefGoogle Scholar; and Ulmer, S. Sidney, “Pairwise Association of Judges and Legislators: Further Reflections,” Midwest Journal of Political Science, XI (02. 1967), 106–115CrossRefGoogle Scholar. The inattention of analysts to the theoretical justification of quantitative indices underscores our previous argument of the need for deriving indices from models with clearly-articulated assumptions about the voting process.

12 Cf. the “axiom of local independence” in Lazarsfeld, Paul F. and Henry, Neil W., Latent Structure Analysis (Boston: Houghton Mifflin Company, 1968), p. 22Google Scholar.

13 What we have specified are, in effect, the “limiting conditions” on the veracity of this axiom. See Simon, Herbert A., “On Judging the Plausibility of Theories,” in van Rootselar, B. and Staal, J. F. (eds.), Logic, Methodology, and Philosophy of Sciences III (Amsterdam: North Holland Publishing Company, 1968), pp. 442ff.Google Scholar

14 For examples in mathematics and physics where “the determinateness of the simple single event and the probabilistic theory of the highly composite whole may seem to be equally compatible …,” see Polya, G., Patterns of Plausible Inference (2d ed.; Princeton, N. J.: Princeton University Press, 1968), p. 194Google Scholar, ftn. 3.

15 Feller, op. cit., p. 3. Italics in original.

16 Friedman, Milton, Essays in Positive Economics (Chicago: University of Chicago Press, 1953), pp. 40–41Google Scholar. For a critique of this viewpoint, see Tjalling C. Koopmans, “The Construction of Economic Knowledge,” in May Brodbeck (ed.), Readings in the Philosophy of the Social Sciences, op. cit., esp. pp. 534–538.

17 Iriji, Yuji and Simon, Herbert A., “Business Firm Growth and Size,” American Economic Review, LIV (03, 1964), 78Google Scholar. Italics in original. We owe this citation to Russett, Bruce M., “Is There a Long-Run Trend Toward Concentration in the International System?” in Russett, (ed.), Economic Theories of International Politics (Chicago: Markham Publishing Company, 1968), p. 312Google Scholar.

18 Waltz, Kenneth N., “Realities, Assumptions, and Simulations,” in Coplin, William D. (ed.), Simulation in the Study of Politics (Chicago: Markham Publishing Company, 1968), p. 106Google Scholar.

19 Later we shall consider various ways to include absentees in the analysis.

20 For the special case in which the voting members of a body are the same across all roll calls, the probability that at least one of the p = t(t − 1)/2 pairs of members agrees on all roll calls is

since [1 − P(AGij)m,m] is the probability that a randomly-selected pair of members disagrees on at least one roll call and [1 − P(AGij) m,m]p is the probability that all pairs of members disagree on at least one roll call. Furthermore, the number of pairs, p, such that the probability is P(AG p≥1) that at least one of the pairs agrees on all roll calls is

since

21 This is true even if the random variables are not mutually independent, as assumed in Axiom 2. While this axiom is not necessary to the proof of Theorem 3, we shall see later that it will prove necessary to the proof of Theorem 8 in the summation of variance across roll calls.

22 If the distribution of votes does not remain constant and only some kinds of votes (say “yes” votes) tend toward infinity as the body becomes larger and larger, then P(AG) will approach a different limit. For the case, for example, where only the “yes” votes approach infinity and the numbers of “no” and “abstain” votes remain finite as t increases,

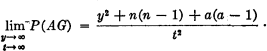
23 See Yamane, Taro, Mathematics for Economists: An Elementary Survey (Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1962), p. 348Google Scholar. When only “yes” and “no” votes are considered, the probability of disagreement will be maximized when the members come as close as possible to a 50–50 split.

24 Though the proposition put forward by Aage R. Clausen that “measures of paired agreements cannot be converted into measures of group cohesion by simple summation” is not entirely clear, the AL index would seem to meet most of the objections raised by Clausen against other indices (in particular, the sensitivity of Grumm's “index of colligation” to group size and its inapplicability to individual roll calls). See Clausen, Aage R., “The Measurement of Legislative Group Behavior,” Midwest Journal of Political Science, XI (05, 1967), 212–224CrossRefGoogle Scholar; and Grumm, John, “The Means of Measuring Conflict and Cohesion in the Legislature,” Southwestern Social Science Quarterly, XLIV (03, 1964), 375–388Google Scholar. It should be noted that the AL index does not allow one to determine the stability of factional alignments in a voting body (a particular AL value may reflect either permanent or shifting cleavages across a set of roll calls), but later in the article we shall develop an index which will be useful in determining the most cohesive voting blocs in a body.

25 World Politics in the General Assembly (New Haven, Conn.: Yale University Press, 1965), p. 255Google Scholar.

26 Ibid.

27 Lijphart, op. cit.

28 Alker and Russett, op. cit., pp. 30–31.

29 “Discovering Voting Groups in the United Nations,” this Review, LX (06, 1966), 327–339Google Scholar.

30 The consequences of such assumptions on the values of correlation coefficients are shown in Galtung, Johan, Theory and Methods of Social Research (New York: Columbia University Press, 1967), pp. 216–218Google Scholar.

31 Alker and Russett, op. cit., p. 30, ftn. 18.

32 Lijphart, op. cit., p. 910, ftn. 41.

33 Alker and Russett, op. cit., p. 30.

34 We append the subscripts i and j to E(AG) in the index to underscore the fact that only the roll calls on which members i and j are both present and voting are used in the calculation of the expected value, E(AGij), for each RAij index. This index is adapted with modifications from one used, among other places, in Brams, Steven J., “Transaction Flows in the International System,” this Review, LX (12., 1966), 880–898Google Scholar; and Brams, Steven J., “Trade in the North Atlantic Area: An Approach to the Analysis of Transformations in a System,” Peace Research Society: Papers, VI (Vienna Conference, 1966), 143–164Google Scholar. Although the transaction-flow model is applied to international transaction data in the above articles, it is not necessary to assume that votes are transactions to use as a measure from the model to analyze voting data. For some purposes, however, the act of agreeing or disagreeing with other members of a voting body might be considered a “symbolic transaction.” Another useful index for measuring agreement between pairs is the phi coefficient, but as used by Ulmer (op. cit.) and others it does not allow for more than two voting options. Jacobsen's measures of “voting agreement” and “voting concordance” do take into account abstention votes, but the theoretical import of these measures is left largely unspecified. See Jacobsen, Kurt, “Voting Behavior of the Nordic Countries in the General Assembly,” Cooperation and Conflict, III, No. 4 (1967), 139–157CrossRefGoogle Scholar.

35 For a review of some of these techniques, see Ball, Geoffrey H., “Data Analysis in the Social Sciences: What About the Details?” Proceedings—Fall Joint Computer Conference, 1965, pp. 533–559Google Scholar; Fortier, J. J. and Solomon, H., “Clustering Procedures,” in Krishnaiah, Paruchuri R. (ed.), Multivariate Analysis (New York: Academic Press, 1966), pp. 493–506Google Scholar; Johnson, Stephen C., “Hierarchical Clustering Schemes,” Psychometrika, XXXII (09., 1967), 241–254CrossRefGoogle Scholar; and Alker, Hayward R. Jr., “Statistics and Politics: The Need for Casual Data Analysis” (paper presented at the Annual Meeting of the American Political Science Association, Chicago, 09 5–8, 1967)Google Scholar. A discussion of the relative merits of different clustering techniques would take us too far afield of our analysis at this time; our attempt here is only to suggest a measure of agreement for all pairs to which these techniques can be applied. We also note in passing that roll calls might be grouped into sets of issues by measuring “agreement” among them across the votes of the members. We can do this by first calculating the “total” probability of agreement for a randomly-selected pair of members on two roll calls as the sum of the products of the P(AG)i's, and P(DG)i's for the two roll calls (assuming they are independent events). For example, for roll calls 1 and 2 given in Table 1, the probability that a randomly-selected pair of members will agree on both roll calls is (.3) (.2) = .06, disagree on both, (.7) (.8) = .56; for a randomly-selected pair, therefore, its “total” probability of agreement (by either agreeing on both roll calls or disagreeing on both roll calls) is .06 + .56 = .62. Since there are 10 pairs of members in a five-member body, the expected number of agreements for the 10 pairs is (10) (.62) =6.2. In fact, for roll calls 1 and 2, 7 of the 10 pairs agree or disagree on both roll calls. In the same way in which we computed RAij for members i and j, we can compute RAij for roll calls as the difference between the actual and expected, divided by the expected, number of pairwise agreements on both roll calls. In the above example.

which indicates a greater-than-expected (i.e., positive) level of “agreement” between roll calls 1 and 2. Thus, while our focus in this article has been on measuring agreement among members across a set of roll calls, the above procedure would allow one to compute RAij indices, analogous to those given in the text, that measure the “agreement” between pairs of roll calls instead of between pairs of members.

36 As with the RAij index, we append the subscript j to E(S) to underscore the fact that only the roll calls on which member j is present and voting are used in the calculation of the expected value, E(Sj), for SLj indices of each member j.

37 A similar statistic is Edward T. Rowe's “win-loss score,” described in his “Changing Patterns in the Voting Success of Member States in the United Nations General Assembly: 1945–1966,” International Organization, 23 (Spring, 1969), 235Google Scholar.

38 William H. Riker (“A Method for Determining the Significance of Roll Calls in Voting Bodies,” op. cit.) has incorporated this idea in his measure of the “significance” of roll-call votes. For a critique of some technical aspects of Riker's index, see Yohe, William P., “Riker's Method for Assessing the Significance of Roll Call Votes,” Public Choice, IV (Spring, 1968), 59–66CrossRefGoogle Scholar.

39 William H. Riker, The Theory of Political Coalitions, op. cit., esp. pp. 32–101.

40 This may in part explain why a majority party in a legislature, of greater than minimal winning size, stays together: it can win on individual roll calls by pulling together different subsets of its members, which may be less costly than relying on one subset (i.e., a single minimal winning coalition with always the same members on each roll call), to hold the line.

41 The standard might even be an ideological position (e.g., liberal versus conservative), where those voting “yes” on some roll calls, and “no” or “abstain” on others, would be interpreted as supportive.

42 This would tend to be the case for the member instrumental in putting together winning coalitions but not for the member simply shrewd enough to foresee the winning position and so align himself with it. This is the “problem of the chameleon,” recognized by Dahl in his attempt to rank the influence of United States Senators on the basis of the differences between the proportion of times a bill passed the Senate when a Senator favored it and the proportion of times a bill passed when he opposed it. See Dahl, Robert A., “The Concept of Power,” Behavioral Science, II (07, 1957), 209–214Google Scholar.

43 For this purpose, a write-up and source deck of a computer program called PROVOTE, which computes all the indices in the model, are available from the Academic Computer Center, New York University, Washington Square, 725 Com-merce Building, New York, N. Y. 10003.

44 This feature of the model would seem to make it especially useful in the study of judicial bodies, whose members may not only associate themselves with or against the majority opinion but may also express particular qualifications in individual affirming or dissenting opinions.

45 Kaplan, Morton A., “Balance of Power, Bipolarity and Other Models of International Systems,” this Review, LV (09., 1957), 695Google Scholar.

46 Rood, Robert M., “Agreement in the International System: An Empirical Test of Balance of Power Theory” (unpublished paper, Syracuse University, 1968.)Google Scholar.

47 Riker, The Theory of Political Coalitions, op. cit.

48 Koehler, David H., “Representational Consensus and the Size Principle” (unpublished paper, Syracuse University, 1968)Google Scholar.

49 An alternative explanation for the constancy in the level of agreement in different sessions might be “situational”: if the ideological differences between the two parties are not great, then the cost of assembling a winning coalition across party lines, often necessary when the majority party has only a small edge over the minority party, would not differ appreciably from the cost of assembling a winning coalition within the majority party when it has a big edge. If the same amount is expended on coalition building in each case, it should buy winning coalitions of approximately the same size. Thus, when ideological differences between parties are slight and a fixed amount (or percentage) of resources tends to be spent on coalition building in a session, the level of agreement in the session should be approximately the same whether one's party majority is large or small.

50 Barnekov, Timothy K., “Measuring Agreement in National Party Conventions” (unpublished paper, Syracuse University, 1969)Google Scholar.

51 We do not wish to stress, however, too rigid a distinction between “concept formation” and “theory formation,” which in Hempel's words “are so closely interrelated as to constitute virtually two different aspects of the same procedure.” Hempel, Carl G., Fundamentals of Concept Formation in Empirical Science (Chicago: University of Chicago Press, 1952), pp. 1–2Google Scholar.

52 For an attempt in this direction, see Brams, Steven J. and Riker, William H., “Models of Coalition Formation in Voting Bodies” (paper presented at the Annual Meeting of the American Association for the Advancement of Science, Boston, 12. 26–31, 1969)Google Scholar; and Brams, Steven J., “A Cost/Benefit Analysis of Coalition Formation in Voting Bodies” (unpublished paper, New York University, 02. 1970)Google Scholar. The assumptions of the models in these papers, however, are not related to those of the present model.

Submit a response

Comments

No Comments have been published for this article.