Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T18:50:29.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Prediction Analysis in Political Research*

Published online by Cambridge University Press:  01 August 2014

David K. Hildebrand ,
James D. Laing  and
Howard Rosenthal
David K. Hildebrand
Affiliation:
University of Pennsylvania
James D. Laing
Affiliation:
Stanford University
Howard Rosenthal
Affiliation:
Carnegie-Mellon University
Get access Rights & Permissions [Opens in a new window]

Extract

Procedures for empirical tests of political theory should be designed to evaluate the success of the specific prediction being tested. This paper introduces; (1) a formal language, termed “prediction logic,” for stating an important class of predictions, including predictions that imply there will be relatively few cases in certain cells of a cross-classification; (2) a population measure, 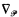(“del”), that indicates the degree of success achieved by a statement in the language; (3) partial measures for the multivariate case; (4) bivariate statistical inference methods when the data arise from a sample rather than a population, both for an a priori prediction statement and for a statement selected post hoc. A number of well-known measures of “association” are 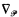measures for specific prediction logic statements. Research applications are indicated through the use of contingency tables appearing in APSR articles by Eulau and Eyestone, Goldberg, Muller, Riker and Zavoina, Rosenthal, Sawyer and MacRae, Sickles, Wolfinger and Field, and Wolfinger and Heifetz.

Type
Articles
Information
American Political Science Review , Volume 70 , Issue 2 , June 1976 , pp. 509 - 535
Copyright
Copyright © American Political Science Association 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 For a more technically detailed presentation of our approach to bivariate prediction and analysis, see our papers “Prediction Logic: A Method for Empirical Evaluation of Formal Theory,” Journal of Mathematical Sociology, 3 (January 1974), 163–185CrossRefGoogle Scholar, and “Prediction Logic and Quasi-Independence in Empirical Evaluation of Formal Theory,” Ibid., pp. 197–209. See also Buchanan, William, “Nominal and Ordinal Bivariate Statistics: The Practitioner's View,” American Journal of Political Science, 18 (August 1974), 625–646CrossRefGoogle Scholar.

2 For an extensive presentation of these methods, see our forthcoming book Prediction Analysis of Cross Classifications (New York: Wiley [Probability and Mathematical Statistics Series: Applied Section])Google Scholar. See also Bartlett, Richard A., “Partition Analysis of Categorical Data,” (Ph.D. dissertation, University of Pennsylvania, 1974)Google Scholar.

3 Lipset, Seymour Martin, Political Man (Garden City, N.J.: Doubleday, 1960), p. 40 (Anchor Edition)Google Scholar; our emphasis.

4 Rosenthal, Howard, “The Electoral Politics of Gaullists in the Fourth French Republic: Ideology or Constituency Interest?” The American Political Science Review, 63 (June 1969), 476–487, at 484CrossRefGoogle Scholar, our emphasis.

5 For an introduction to elementary formal logic and truth tables, see Kemeny, John G., Snell, J. Laurie and Thompson, Gerald L., Introduction to Finite Mathematics, 3rd edition (Englewood Cliffs, N.J.: Prentice-Hall, 1974)Google Scholar or Suppes, Patrick, Introduction to Logic (Princeton, N.J.: D. Van Nostrand, 1957), Part IGoogle Scholar.

6 Rapoport, Anatol, N-Person Game Theory (Ann Arbor: University of Michigan Press, 1970), p. 269Google Scholar; first emphasis ours.

7 Francis, Wayne L., “Influence and Interaction in a State Legislative Body,” The American Political Science Review, 56 (December 1962), 953–960, at 954CrossRefGoogle Scholar.

8 Ibid., p. 955.

9 This proposition can be operationalized into a specific prediction logic proposition about the relative position of pairs of observations on the two variables. We describe this procedure later in the paper.

10 Wolfinger, Raymond E. and Field, John Osgood, “Political Ethos and the Structure of City Government,” The American Political Science Review, 60 (June 1966), 306–326, at 313–314CrossRefGoogle Scholar.

11 For an extensive application of our methods to analyze propositions more complex than any examples considered in this paper, see Laing, James D. and Morrison, Richard J., “Sequential Games of Status,” Behavioral Science, 19(May 1974), 177–196CrossRefGoogle Scholar. Also, see Friend, Kenneth E., Laing, James D., and Morrison, Richard J., “Game-Theoretic Analyses of Coalition Behavior,” a paper presented at the 1974 Annual Meeting of the American Political Science Association, Palmer House, Chicago, Illinois, August 29–September 2, 1974Google Scholar. For an application in economics, see Korteweg, Pieter, “The Inflation Problem: A Multi-Country Study of Inflation—The Dutch Case 1952–1972” (Rotterdam: Netherlands School of Economics Working Paper 741, 1974), a paper presented at Eastern Economic Association meetings, Albany, New York, October 25–27, 1974Google Scholar.

12 For a discussion of our methods when certain cells are omitted from the proposition's domain and, hence, should be excluded from the analysis, see Hildebrand, Laing, and Rosenthal, , “Prediction Logic and Quasi-Independence ….,” p. 203Google Scholar, and Hildebrand, Laing and Rosenthal, Prediction Analysis of Cross Clasifications, chap. 4. For an extensive application of these methods, see Laing and Morrison, “Sequential Games of Status,”

13 See Hildebrand, David K., Laing, James D. and Rosenthal, Howard, “A Prediction Logic Approach to Causal Models of Qualitative Variates,” Sociological Methodology, 1976, ed. Heise, D. (San Francisco: Jossey-Bass, 1975), pp. 146–175Google Scholar.

14 Riker, William H. and Zavoina, William James, “Rational Behavior in Politics: Evidence from a Three-Person Game,” The American Political Science Review, 64 (March 1970), 48–60, at 58CrossRefGoogle Scholar; our emphasis.

15 Muller, Edward N., “A Test of a Partial Theory of Potential for Political Violence,” The American Political Science Review, 66 (September 1972), 936CrossRefGoogle Scholar.

16 Eulau, Heinz and Eyestone, Robert, “Policy Maps of City Councils and Policy Outcomes: A Developmental Analysis,” The American Political Science Review, 62 (March 1968), 124–143, at 129–130CrossRefGoogle Scholar.

17 Sawyer, Jack and MacRae, Duncan Jr., “Game Theory and Cumulative Voting in Illinois: 1902–1954,” The American Political Science Review, 56 (December 1962), 936–946CrossRefGoogle Scholar.

18 Coleman, James S., Introduction to Mathematical Sociology (New York: The Free Press of Glencoe, 1964), p. 516Google Scholar.

19 By this criterion, the measure will be identical for logically equivalent propositions, whether X is used to predict Y, or Y is used to predict X. However, for some research applications it may be useful to treat the variables asymmetrically in accordance with their roles as predictor and predicted. Methods for this are discussed in Hildebrand, Laing, and Rosenthal, Prediction Analysis of Cross Classifications, section 4.3.

20 See, for example, Goodman, Leo A., “The Analysis of Cross-Classified Data; Independence, Quasi-Independence, and Interactions in Contingency Tables With or Without Missing Entries,” Journal of the American Statistical Association, 63 (December, 1968), 1091–1131Google Scholar, and Goodman, Leo A., “How to Ransack Social Mobility Tables and Other Kinds of Cross-Classification Tables,” American Journal of Sociology, 75 (July 1969), 1–40CrossRefGoogle Scholar.

21 Kang, Tai S., “Linking Form of a Hypothesis to Type of Statistics: an Application of Goodman's Z,” American Sociological Review, 37 (July 1972), 357–365CrossRefGoogle Scholar.

22 Goodman, Leo A. and Kruskal, William H., “Empirical Evaluation of Formal Theory,” Journal of Mathematical Sociology, 3 (January 1974), 187–196CrossRefGoogle Scholar.

23 See David K. Hildebrand, James D. Laing, and Howard Rosenthal, “Prediction Logic and Quasi-independence in Empirical Evaluation of Formal Theory,” and Laing, and Rosenthal, , “Linking Form of Hypothesis to Type of Statistic: Comment,” American Sociological Review, 39 (April 1974), 277–280CrossRefGoogle Scholar.

24 For discussions of these three respective techniques, see for example, Hoel, Paul G., Port, Sidney C., and Stone, Charles J., Introduction to Statistical Theory (Boston: Houghton Mifflin, 1971)Google Scholar, sections 3.5 and 3.4, and Theil, Henri, “On the Estimation of Relationships Involving Qualitative Variables,” American Journal of Sociology, 76 (July 1970), 103–154CrossRefGoogle Scholar.

25 Costner, Herbert L., “Criteria for Measures of Association,” American Sociological Review, 30 (June, 1965), 341–353CrossRefGoogle Scholar.

26 Goodman, Leo A. and Kruskal, William H., “Measures of Association for Cross-Classifications II: Further Discussion and References,” Journal of the American Statistical Association, 54 (March 1959), 123–163, at 133CrossRefGoogle Scholar.

27 In effect, Goodman and Kruskal, and Costner, “Criteria for Measures of Association,” look at the sign of y before choosing a prediction rule. (See Goodman, Leo A. and Kruskal, William H., “Measures of Association for Cross Classifications,” Journal of the American Statistical Association, 49 [December 1954], 732–764.Google Scholar) If y >0, then they use the prediction given in Table 9. On the other hand, if y >0, they use the prediction rule , interpreting the absolute value of gamma as the PRE afforded by this ex post prediction. If, in contrast, one specifies one of the a priori predictions in the table, y <0 simply indicates a proportionate increase in error resulting from an unsuccessful prediction.

28 For further development and technical details of the statistical methods for evaluating a priori and ex post prediction logic propositions, see Hildebrand, Laing and Rosenthal, Prediction Analysis of Cross Classifications, chapter 6 and Wasserman, Stanley, “An Ex Post Significance Test for a Pattern of Association Based on Prediction Logic” (M.S. thesis, University of Pennsylvania, 1973)Google Scholar.

29 Hildebrand, Laing and Rosenthal, “Prediction Logic: A Method for Empirical Evaluation of Formal Theory,” and “Errata,” Journal of Mathematical Sociology (in press).

30 Cramér, Harold, Mathematical Methods of Statistics (Princeton, N.J.: Princeton University Press, 1946)Google Scholar, and Wilks, S. S., Mathematical Statistics (New York: Wiley, 1962), p. 260Google Scholar.

31 Sickels, Robert J., “The Illusion of Judicial Consensus: Zoning Decisions in the Maryland Court of Appeals,” The American Political Science Review, 59 (March 1965), 100–104CrossRefGoogle Scholar.

32 The fact that it should be difficult to decide which proposition is “best” should not be surprising. For some-what different reasons, for example, it may not be clear whether the “best” functional relation between two interval variables is linear, quadratic, logarithmic, etc.

33 Goldberg, Arthur S., “Social Determinism and Rationality as Bases of Partly Identification,” The American Political Science Review, 63 (March 1969), 5–25CrossRefGoogle Scholar.

34 Although Goldberg's variables are ratio scales, he presents the data collapsed into ordinal categories. Also, Goldberg's independent and dependent variables are not measured independently as is required for application of . However, the confounding introduced by the latter aspect of his techniques should be minor.

35 Moreover, the τb measure is designed for nominal data and could show high values when data contradict Goldberg's theory. We suspect Goldberg used it because τb measures an (ex post) prediction of single observations whereas conventional ordinal measures such as y are restricted to the prediction of observation pairs.

36 Goldberg, pp. 12–13. A note of caution. The type of ex post analysis we conducted with Goldberg's data can lead to an overestimate of the value with small samples. The overestimation is negligible with samples as large as Goldberg's. See Bartlett, “Partition Analysis of Categorical Data.”

37 Ibid., p. 13.

38 In this paper we do not consider how non-binary error weights for bivariate propositions should be treated when these propositions are logically connected to yield a multivariate prediction. For example, if an error event for the multivariate prediction is also an error event for two distinct bivariate components, and the event is weighted differently for these components, then what weight should be used in analyzing the multivariate prediction?

In this paper we assume either that unweighted errors are used or that the error weights are given directly for the multivariate prediction.

39 Wolfinger, Raymond E. and Heifetz, Joan, “Safe Seats, Seniority, and Power in Congress,” The American Political Science Review, 59 (June 1965), 337–349, at 339CrossRefGoogle Scholar.

40 Rosenthal, Howard, “Voting and Coalition Models in Election Simulations,” Simulation and the Study of Politics, ed. Coplin, William, (Chicago: Markham, 1968), pp. 237–287, at pp. 279–280Google Scholar.

Submit a response

Comments

No Comments have been published for this article.