Introduction
The use of locally available natural and recycled feedstock for construction is being actively studied, as it is a promising option for sustainability by reducing energy inputs and carbon emissions during the fabrication and transportation of the feedstock. Aligned with this effort, stone masonry, one of the oldest types of construction utilizing natural stones, is being rediscovered due to its unique advantages: significantly lower embodied energy/carbon than other building materials (Venkatarama Reddy and Jagadish, Reference Venkatarama Reddy and Jagadish2003). Figure 1 illustrates that stones provide the strength of concrete with a thousandth less embodied energy of steel (ANSYS Granta, 2019). In this context, stone masonry could become an attractive option to achieve a sustainable construction industry, as embodied energy/carbon is one of the most important factors to consider for the sustainability of the construction industry (Hegger et al., Reference Hegger, Fuchs, Stark and Zeumer2012). In addition, the advancement of robotic construction is expected to remove a major obstacle in stone masonry construction by automating labor-intensive tasks [e.g., bricklaying robots (Sklar, Reference Sklar2015) and a masonry construction drone (Goessens et al., Reference Goessens, Mueller and Latteur2018)].

Figure 1. The comparison chart of embodied energy versus strength for different construction materials, created with CES EduPack 2019 (ANSYS Granta, 2019).
While labor-intensive tasks have been the obstacle in stone masonry construction, the high dependence on domain knowledge is a major limiting factor in stone masonry design. Stone masonry designs are typically done by highly experienced experts with a great amount of (often ad hoc) domain knowledge in structural design, material science, and geometry. Thus, the construction industry has moved toward engineered masonry units (EMUs) that are highly regular and uniform, requiring less skill and domain knowledge during design and construction. Current practices in the analysis and design of masonry structures mostly assume the use of EMUs. Four categories of modeling are common: block-based models, continuum models, geometry-based models, and macro-element models (D'Altri et al., Reference D'Altri, Sarhosis, Milani, Rots, Cattari, Lagomarsino, Sacco, Tralli, Castellazzi and de Miranda2020). Based on analytical modeling, masonry designs follow several design codes or empirical rules (e.g., American code including ACI 530-02/ASCE 5-02/TMS 402-02 (Masonry Standards Joint Committee, 2002), or employ design techniques such as limit state design or allowable stress design (Theodossopoulos and Sinha, Reference Theodossopoulos and Sinha2013). As their names imply, limit state design and permissible stress design aim at enforcing “limit state” or “permissible stress”, which is the boundary between feasible and infeasible design, to maintain the design within given constraints. In addition, computer-aided design methods to support EMU masonry structure design have been also developed, including the automatic unit layout method proposed by Liu et al. (Reference Liu, Cao, Xue, Li, Feng and Frank Chen2021). However, unlike EMU masonry, applying the aforementioned approaches to stone masonry is not straightforward, as it involves complex interactions among heterogeneous and irregular natural stones and mortar joints. The high dependence on domain knowledge (i.e., human experts) is an important challenge, as the architectural knowledge regarding stone masonry design has been waning (Gentry, Reference Gentry2013). There are some pioneering works demonstrating the use of heterogeneous sizes of cuboidal blocks to incorporate a wider range of construction materials (e.g., from 3D printing or brick-making) (Zhang and Shea, Reference Zhang and Shea2022), but the extension of the method to various shapes is necessary to address stone masonry design problems.
Topology optimization (TO) – the optimization of material distribution within a design space (Sigmund and Maute, Reference Sigmund and Maute2013) – is an established research area and has been successfully applied to the design of customized structures made with additive manufacturing (Guo and Leu, Reference Guo and Leu2013; Laureijs et al., Reference Laureijs, Roca, Narra, Montgomery, Beuth and Fuchs2017; Amir and Mass, Reference Amir and Mass2018). The two common TO approaches are density-based TO and level-set methods. While most TO applications consider the case where a design can be described as the distribution of a single type of material (e.g., 3D printing filament), advances are being made with heterogeneous materials like composite or cellular material (Andreassen and Jensen, Reference Andreassen and Jensen2014; Coelho et al., Reference Coelho, Guedes and Cardoso2019) and multiple materials (Wang and Wang, Reference Wang and Wang2004; Vogiatzis et al., Reference Vogiatzis, Chen, Wang, Li and Wang2017; Zuo and Saitou, Reference Zuo and Saitou2017), opening the capability of TO beyond isotropic solids. Additionally, the efficiency of TO has been improved with machine learning (ML) methods such as support vector regression (Lei et al., Reference Lei, Liu, Du, Zhang and Guo2018) and deep neural networks (DNN) (Chandrasekhar and Suresh, Reference Chandrasekhar and Suresh2021). Design constraints are an important aspect of TO for practical applications. For example, 3D printing designs must be constrained to the feasible ranges of feature size and overhang angle of the printer. However, few, if any, TO approaches consider material availability constraints, such as the availability of different sizes of natural stone. Further complicating the use of TO for stone masonry, stone masonry structures with the same silhouette may exhibit completely different performances, as heterogeneous masonry units and their joints should be carefully organized in a proper order to ensure the functionality of the stone masonry structure as a whole. This also indicates that the continuity, convexity, and smoothness of objective function are not guaranteed when TO is used for stone masonry design, as just a single change of design (e.g., changing a stone in the middle) can completely change the behavior of the overall stone masonry structure. Simply put, the nature of stone masonry design makes it difficult to apply current TO methods.
ML and artificial intelligence (AI) are also actively adopted in architectural design and analysis in different stages (Sun et al., Reference Sun, Burton and Huang2021). For example, AI methods, especially evolutionary algorithms, have been adopted to support the exploration of conceptual designs (Wang et al., Reference Wang, Janssen and Ji2020), layout designs (Su and Yan, Reference Su and Yan2015; Baghdadi et al., Reference Baghdadi, Heristchian and Kloft2020; Liu et al., Reference Liu, Liu, Feng, Wu, Li and Frank Chen2020), and detailed designs of structural members (Ahlquist et al., Reference Ahlquist, Erb and Menges2015; Hofmeyer and Delgado, Reference Hofmeyer and Delgado2015). As ML and AI methods are founded upon computational analysis (e.g., finite element method, FEA), building surrogate models to accelerate the assessment of architectural structure has been also investigated to facilitate design exploration (Wortmann et al., Reference Wortmann, Costa, Nannicini and Schroepfer2015; Zheng et al., Reference Zheng, Moosavi and Akbarzadeh2020). Other approaches also include the evaluation of architectural designs in quantitative aspects, such as visual design principles, esthetics, and creativity (Mars et al., Reference Mars, Grabska, Ślusarczyk and Strug2020; Demir et al., Reference Demir, Çekmiş, Yeşilkaynak and Unal2021). However, existing approaches still cannot address the challenges involving stone masonry designs: organizing heterogeneous shapes of natural stones in proper order considering the complex interaction across their joints, without prescribed knowledge.
RL has shown promising results to learn effective strategies (i.e., taking a proper sequence of timely action), allowing gaming AI to conquer even extremely complex computer games. For example, AlphaStar (Vinyals et al., Reference Vinyals, Babuschkin, Czarnecki, Mathieu, Dudzik, Chung, Choi, Powell, Ewalds, Georgiev, Oh, Horgan, Kroiss, Danihelka, Huang, Sifre, Cai, Agapiou, Jaderberg, Vezhnevets, Leblond, Pohlen, Dalibard, Budden, Sulsky, Molloy, Paine, Gulcehre, Wang, Pfaff, Wu, Ring, Yogatama, Wünsch, McKinney, Smith, Schaul, Lillicrap, Kavukcuoglu, Hassabis, Apps and Silver2019) and OpenAI Five (OpenAI et al., Reference Berner, Brockman, Chan, Cheung, Dębiak, Dennison, Farhi, Fischer, Hashme, Hesse, Józefowicz, Gray, Olsson, Pachocki, Petrov, d.O. Pinto, Raiman, Salimans, Schlatter, Schneider, Sidor, Sutskever, Tang, Wolski and Zhang2019) triumphed against the world's top professional human players in complex strategy computer games like StarCraft II and DOTA 2. Due to the aforementioned capability, RL has been actively adopted in many design problems, including drug design (Popova et al., Reference Popova, Isayev and Tropsha2018), microfluidic device design utilizing different micro-pillars to get desired fluid flow profile (Lee et al., Reference Lee, Balu, Stoecklein, Ganapathysubramanian and Sarkar2019), automatic generation of FEA meshes from heterogeneous boundary shapes (Pan et al., Reference Pan, Huang, Wang, Cheng and Zeng2021), and plane truss design using heterogeneous sizes of beams/columns for different stories of a building (Hayashi and Ohsaki, Reference Hayashi and Ohsaki2021). In other words, the challenges involving stone masonry design can potentially be addressed when the demonstrated capabilities of RL are used in a synergistic manner: solving design problems involving heterogeneous design units; and learning a proper sequence of action shown through gaming AI. Therefore, if there is a virtual design environment for stone masonry design, the success of RL in gaming AI and design problems can be translated to stone masonry design, due to its ability to learn optimal design decisions at each time step without prescribed domain knowledge. In the meantime, the classic computer game Tetris is analogous to stone masonry in some ways as shown in Figure 2. Specifically, both stone masonry and Tetris organize heterogeneous design units to form an overall structure, where the order of placing each design unit matters, and the score is determined by the topology of the overall structure. Therefore, with some modifications to Tetris (e.g., design units, score calculation, etc.), it is possible to develop a virtual design environment, where AI agents can autonomously learn effective stone masonry design policies via trial-and-error in the context of RL.
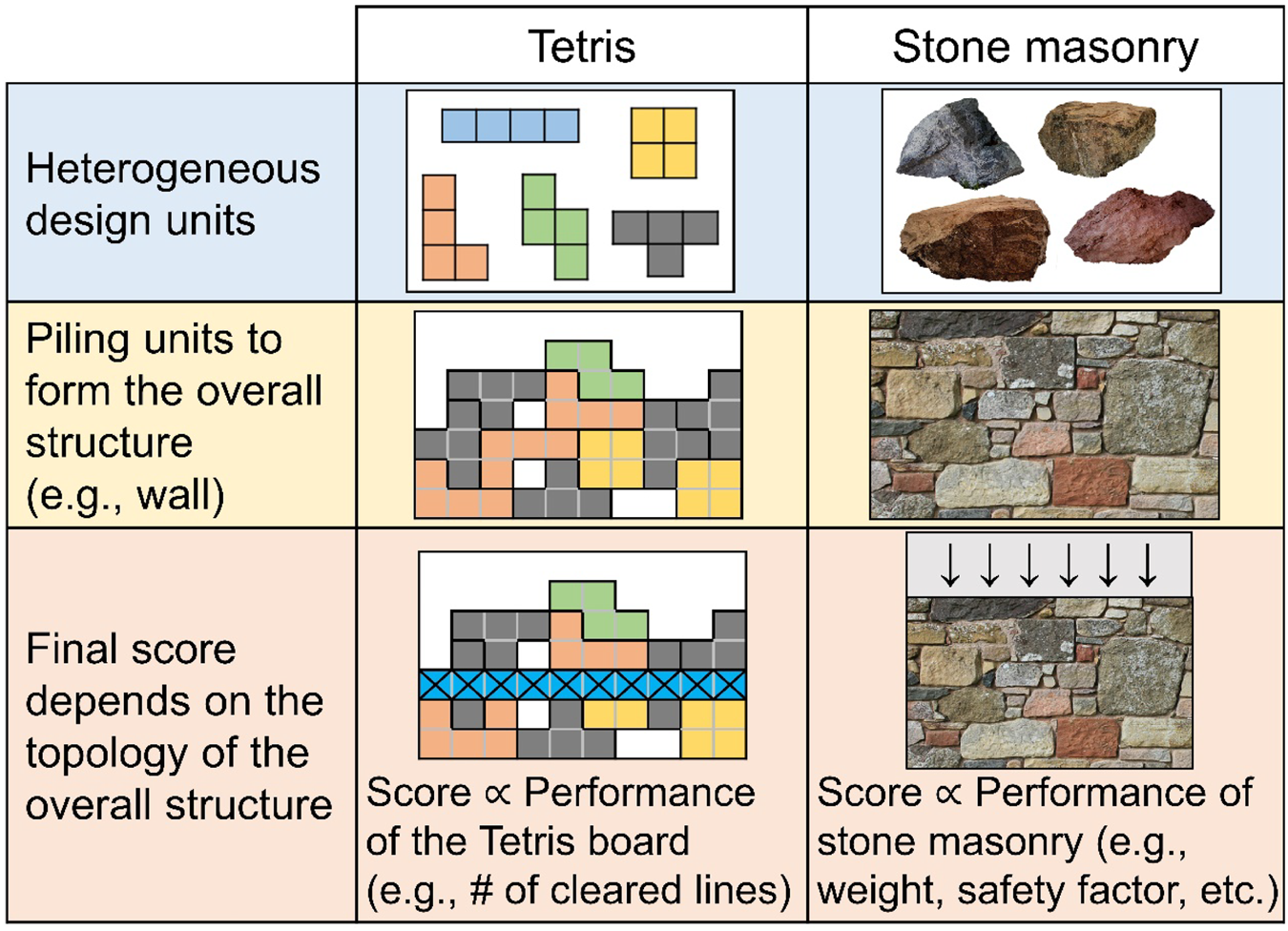
Figure 2. The analogy between Tetris and stone masonry.
In this context, this paper aims to answer the following research question: “can an RL framework learn effective stone masonry design policy without prescribed knowledge, when coupled with a virtual design environment inspired by a similar puzzle game (i.e., Tetris)”. It is an important research question, as it will not only help investigate the stone masonry design problem, but also can be generalized to address other practical design problems with similar design challenges, opening opportunities in design automation for sustainability: the use of locally available natural and recycled feedstock with stochastic, sequential, and heterogeneous nature (e.g., timber feedstock with random defects). To address the research question, a virtual design environment, called MasonTris, is designed by integrating a custom emulator of Tetris with an FEA tool, OpenSeesPy (Zhu et al., Reference Zhu, McKenna and Scott2018), to evaluate the fitness (i.e. weight and safety factor) of a given stone masonry design (i.e., arrangement of polyominoes). Founded upon MasonTris, the proposed RL framework autonomously explores topological structures by placing polyominoes (i.e., Tetris-like workpieces), learning stone masonry design policy to improve the fitness (i.e., reward). This iterative exploration is guided by double deep Q-learning (DDQN) (Hasselt et al., Reference Hasselt, Guez and Silver2016) to learn effective stone masonry design policies (i.e., understand where to place polyominoes to achieve higher rewards). The DDQN approach has seen success in domains such as edge scheduling (Zhang et al., Reference Zhang, Lin, Yang, Chen, Khan and Li2019) and autonomous vehicle speed control (Zhang et al., Reference Zhang, Sun, Yin, Lin and Wang2018). The feasibility of the proposed framework is demonstrated in a simplified but still realistic approximation of stone masonry design problems founded upon Tetris, called MasonTris problems. If successful, such a framework could be paired with advanced robotics to automate the design and construction of sustainable stone masonry. For example, a user (likely a building designer who is familiar with building design in general but not familiar with stone masonry design) can provide the requirements (e.g., safety constraints) to the proposed framework, and then monitor/review the evolution of designs. Once the proposed framework learns the design policy and the user is satisfied with the best design so far, the user can retrieve the best design as the final design. The final design may be the global optimal design if the user has access to enough computation resource/time or a promising design that the user can polish for the purpose. In other words, the proposed framework will help the designer to save a significant amount of time involving trial-and-errors during the stone masonry design process. The novelties of the proposed work are as follows:
• A virtual design environment for stone masonry, MasonTris, is designed based on the analogy between Tetris and stone masonry. MasonTris is a powerful, yet simple, analogy to stone masonry, with core similarities shown in Figure 2, where its components and reward structure are carefully designed to represent stone masonry design.
• The proposed RL framework adopts a novel design exploration policy, called almost-greedy policy, to balance exploration and exploitation to improve the stability of learning. Almost-greedy policy is especially useful for design problems with sparse reward (i.e., only a small portion of designs are feasible in the design space).
• Unlike typical RL frameworks, the proposed RL framework evaluates and calculates the rewards only when the data is fed to improve design policy. The proposed modification prevents the computation bottleneck when multiple AI agents simultaneously explore and calculate rewards on-the-fly. This significantly improves the efficiency of design exploration in a practical scenario, where the evaluation of each design candidate is time-consuming, thus desirable to be parallelized.
This work has three broader contributions in the areas of TO, RL, and design automation. For the general TO community, this work demonstrates RL as a tool to optimize topological structure incorporating heterogeneous design units, as opposed to the traditional uniform voxels, where typical TO methods are not effective. It should be noted that design problems involving heterogeneous design units are becoming more important, as the use of sustainable natural material (e.g., timber) and recycled/reused material is limited by their heterogeneity in nature. In other words, the proposed framework helps overcoming the barrier to the broader adoption of such sustainable materials. For the broader RL community, the proposed framework adopts on-demand calculation of costly reward evaluation for efficient parallelization, as well as an effective design collection policy to address sparse reward problems. This will promote the use of RL frameworks to solve challenging practical engineering problems. Lastly, for the broader design automation community, this work illustrates the potential for RL to learn domain-specific knowledge from scratch in a simplified virtual environment. Upon the development of a corresponding virtual environment, the framework can be applied to a wide variety of different design problems at various scales and various materials, similar to the way that a game was developed to allow game players to help protein structure design (Khatib et al., Reference Khatib, Cooper, Tyka, Xu, Makedon, Popović, Baker and Players2011).
Background
Reinforcement learning
RL is a discipline of ML, which involves identifying an optimal policy for a sequential decision-making problem (Sutton and Barto, Reference Sutton and Barto1998) through the iterative improvement of the learned policy. The improvement of the policy is guided by a reward that is typically provided sporadically – that is, when a goal (or an intermediate goal) is achieved. Therefore, the main focus of RL is to identify which action can maximize the expectation of the sum of future rewards, even when the reward is not provided yet. Generally, the more sporadic the reward, the more challenging the RL problem. Many practical problems have been solved with RL, for example, robot control, military planning, and power management (Roijers et al., Reference Roijers, Vamplew, Whiteson and Dazeley2013).
In RL, a sequential decision-making problem is typically formulated with the interactions between agents and the surrounding environment. Three variables can describe the evolution of such a system in discrete time and space: (1) the state s that describes the state of the surrounding environment, (2) action a that the agent can take to trigger the transition between different states, (3) and reward r that indicates how good or bad the outcome of an action is. An agent has a policy π that maps the state to an action that results in a new state (i.e., determines which action to take given the state of the surrounding environment). At each time step, the agent may earn a reward computed from the current state. The agent's goal is to improve the policy, towards an optimal π*, at each step to maximize the reward earned over the time horizon. The agent may learn from multiple episodes of actions from initial to final states as the system evolves.
Double DDQN
Deep Q-Learning (DQN) (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Graves, Antonoglou, Wierstra and Riedmiller2013) is a widely adopted RL method that learns an action-value function ![]() $Q_\theta ( {s, \;a} )$, also known as the Q-value, by using a DNN. θ is the vector of parameters of the DNN that defines the function. Practically, this function estimates the cumulative future rewards at time step t (i.e.,
$Q_\theta ( {s, \;a} )$, also known as the Q-value, by using a DNN. θ is the vector of parameters of the DNN that defines the function. Practically, this function estimates the cumulative future rewards at time step t (i.e., ![]() $Q_\theta ( {s, \;a} ) = {\rm {\mathbb E}}\left[{\sum\nolimits_{k = 0}^{T-t} {\gamma^k\;r_{t + k}\vert s_t = s, \;a_t = a} } \right]$) when an action a is chosen at a state s, where γ is a discount factor to the future reward and T is the unknown time step of the terminal state.
$Q_\theta ( {s, \;a} ) = {\rm {\mathbb E}}\left[{\sum\nolimits_{k = 0}^{T-t} {\gamma^k\;r_{t + k}\vert s_t = s, \;a_t = a} } \right]$) when an action a is chosen at a state s, where γ is a discount factor to the future reward and T is the unknown time step of the terminal state.
In each RL iteration, a DNN is updated to learn the action-value function. The DNN is then used by the agent to identify the action in the current state that maximizes this function. In other words, the policy π of DQN is not explicitly modeled, but indirectly modeled by deriving the value of each action in a finite action space, and choosing the action yielding the maximum value. DNN's proven ability to precisely approximate complex relations provides DQN with an effective policy, even for problems with a huge state space.
This paper uses DDQN (Hasselt et al., Reference Hasselt, Guez and Silver2016), a more stable variant of DQN. A DDQN agent improves its DNN approximation of the action-value function through the following procedure:
• Initialization: The untrained agent begins with a random policy where a uniformly random action a is selected within the set of feasible actions
 ${\cal A}$ (i.e., available polyominoes and rotations, or episode termination) to explore a number of episodes. Each action in each episode generates an experience that can be represented by the tuple e t = {s t, a t, r t, s t+1} that is added to an experience replay buffer (Lin, Reference Lin1992). The agent then initializes a DNN with parameters θ drawn from a Glorot uniform distribution (Glorot and Bengio, Reference Glorot and Bengio2010) with bounds determined by the number of inputs/outputs. This DNN is then trained from a random sample of the experience replay using the process below.
${\cal A}$ (i.e., available polyominoes and rotations, or episode termination) to explore a number of episodes. Each action in each episode generates an experience that can be represented by the tuple e t = {s t, a t, r t, s t+1} that is added to an experience replay buffer (Lin, Reference Lin1992). The agent then initializes a DNN with parameters θ drawn from a Glorot uniform distribution (Glorot and Bengio, Reference Glorot and Bengio2010) with bounds determined by the number of inputs/outputs. This DNN is then trained from a random sample of the experience replay using the process below.• Exploration and training iterations: The agent begins each RL iteration by exploring a small number of new episodes (saving each experience in the replay buffer). Exploration and exploitation are balanced with an
 $\varepsilon$-greedy policy. This policy is generally greedy, choosing an action according to Eq. (1), but may choose a uniformly random feasible action with probability
$\varepsilon$-greedy policy. This policy is generally greedy, choosing an action according to Eq. (1), but may choose a uniformly random feasible action with probability  $\varepsilon$. Training in each RL iteration uses a random subset of the experience replay to update the θ parameters of the DNN using gradient descent. Choosing a random batch rather than the most recent experiences significantly improves the training reliability and sample efficiency (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Graves, Antonoglou, Wierstra and Riedmiller2013). The “double” in DDQN refers to the joint use of two DNNs with the same architecture but different parameters: an online model Q where its parameters are denoted as θ and a target model Q ′ where its parameters are denoted as θ ′ (Hasselt et al., Reference Hasselt, Guez and Silver2016). Exploration of new experiences are done with Q. Then Q and Q ′ are jointly used in the training of DNN to approximate the ground-truth action-value function Q* via Eq. (2), where Q is used to identify an action and Q ′ is used to evaluate the value of the selected action to update the approximation of Q*. The target model, Q ′, is periodically updated by copying over the parameters θ from Q according to Eq. (3) for the reliability of the training (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Graves, Antonoglou, Wierstra and Riedmiller2013).(1)
$\varepsilon$. Training in each RL iteration uses a random subset of the experience replay to update the θ parameters of the DNN using gradient descent. Choosing a random batch rather than the most recent experiences significantly improves the training reliability and sample efficiency (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Graves, Antonoglou, Wierstra and Riedmiller2013). The “double” in DDQN refers to the joint use of two DNNs with the same architecture but different parameters: an online model Q where its parameters are denoted as θ and a target model Q ′ where its parameters are denoted as θ ′ (Hasselt et al., Reference Hasselt, Guez and Silver2016). Exploration of new experiences are done with Q. Then Q and Q ′ are jointly used in the training of DNN to approximate the ground-truth action-value function Q* via Eq. (2), where Q is used to identify an action and Q ′ is used to evaluate the value of the selected action to update the approximation of Q*. The target model, Q ′, is periodically updated by copying over the parameters θ from Q according to Eq. (3) for the reliability of the training (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Graves, Antonoglou, Wierstra and Riedmiller2013).(1) $$a = \mathop {{\rm argmax}}\limits_{a\in {\cal A}} Q_\theta ( {s, \;a} ) $$(2)
$$a = \mathop {{\rm argmax}}\limits_{a\in {\cal A}} Q_\theta ( {s, \;a} ) $$(2) $$Q^\ast ( {s_t, \;a_t} ) \approx r_t + \gamma {Q}^{\prime}\left({s_{t + 1}, \;\;\mathop {{\rm argmax}}\limits_{a\in {\cal A}} Q_\theta ( {s_{t + 1}, \;a} ) } \right)$$(3)
$$Q^\ast ( {s_t, \;a_t} ) \approx r_t + \gamma {Q}^{\prime}\left({s_{t + 1}, \;\;\mathop {{\rm argmax}}\limits_{a\in {\cal A}} Q_\theta ( {s_{t + 1}, \;a} ) } \right)$$(3) $${\theta }^{\prime}\leftarrow \gamma \theta + ( {1-\tau } ) {\theta }^{\prime}, \;\;\;0 \le \tau \le 1$$
$${\theta }^{\prime}\leftarrow \gamma \theta + ( {1-\tau } ) {\theta }^{\prime}, \;\;\;0 \le \tau \le 1$$• Evaluation/termination: RL agents are typically trained for a sufficiently-large fixed number of iterations or a fixed amount of wall-clock time. Training duration is typically assumed to be sufficient when the reward stabilizes to the observed maximum with the hope that the policy [Eq. (1)] approximates the optimal policy.
Methods
Problem definition: MasonTris problem
This manuscript considers a simplification of the stone masonry design problem illustrated by Figure 3. This problem, herein named MasonTris problem, is inspired by Tetris combined with a structural analysis using FEA. It includes the following components: (1) a 2D design space and outer shell, (2) a source of polyominoes, which are the geometric shapes composed of one or multiple squares connected orthogonally (e.g., Tetris workpieces are 4-block “tetrominoes”), to be stacked within the design space to form a structure to support (3) an external load applied to the outer shell surface(s). MasonTris incorporates the most distinct characteristics of stone masonry design, irregular sizes/shapes of natural stones, by approximating natural stones with polyominoes, which can be regarded as low-resolution pixelized versions of natural stones. As polyominoes can represent various shapes (i.e., not necessarily versatile cuboidal shapes found in EMUs), similar to the shapes of natural stones found in stone masonry, we assume that such polyominoes are suitable to validate the feasibility of the proposed framework in a simplified setting. Note, unlike the classic video game, various polyomino sizes are considered, there is an unbounded supply of each polyomino considered (i.e., any available polyomino can be selected for an action), complete lines are not eliminated, and an agent can decide when an episode terminates; otherwise, the episode terminates when no polyomino can be placed.

Figure 3. The motivating example of the autonomous stone masonry design framework (MasonTris problem).
In this paper, the objective of MasonTris problem is to learn an action-value function Q* that yields an optimal policy π*, for sequentially building a structure with polyominoes that satisfies a maximum-stress safety factor, with minimal weight. The following actions, states, and rewards define this objective as an RL problem. The actions a are the type of polyomino to place and where to place it (i.e., with a “hard drop” from the top of the board). The state s is in a 2D grid state space indicating the location of each polyomino and interstitial grout. The reward r is increased by reducing the weight of a structure, while maintaining an adequate safety factor calculated from the maximum stress of the FEA. Traditional Q-learning would construct a table for each possible action in each possible state, which is intractable for all but the smallest structural design spaces. For example, a standard Tetris game (i.e., board size: 10 × 20) is estimated to have 7 × 2200 states (Algorta and Şimşek, Reference Algorta and Şimşek2019). Instead, this paper proposes a DDQN as an efficient way to learn such a policy with reasonable computational resources. The findings may be applicable to more sophisticated stone masonry problem (e.g., by adopting more sophisticated reward calculation) or extended to other domains with problems that can be defined similarly (e.g., mass timber building design).
Proposed framework overview
The proposed RL framework, shown in Figure 4, consists of the MasonTris environment (top-left of Fig. 4), a DDQN agent (top-right of Fig. 4), and a trainer (bottom of Fig. 4). The MasonTris environment defines the available polyominoes and how they can be stacked within the design space. The DDQN agent explores (in parallel) many episodes in the design space to learn a policy (periodically updated by the trainer) for stacking polyominoes that maximize its reward. The trainer keeps a record of all the agent's experiences (i.e., the tuple {s t, a t, r t, s t+1}) and feeds a random subset to the agent in the RL iteration. The trainer also calculates the reward using FEA.

Figure 4. An overview of the proposed stone masonry design AI framework.
To solve the MasonTris problem, the following three innovations were introduced in the following sub-sections respectively: (1) The MasonTris environment was developed to test different AI/RL approaches to the stone masonry design problem; (2) In addition to typical ɛ-greedy policy, additional ɛ-greedy policy called almost-greedy policy is jointly used. Almost-greedy policy is designed to facilitate exploration in the sparse space of feasible designs in MasonTris problem; (3) A modification to the experience replay technique such that rewards are only calculated on-demand (and in parallel) to address the significant computational cost of reward calculation compared to other applications of DDQN.
MasonTris environment
The proposed RL framework incorporates MasonTris environment, which can be regarded as a modified version of Tetris to address stone masonry design problems. Figure 5 provides an overview of the MasonTris environment. MasonTris environment provides a meaningful example of designing a virtual environment based on a simple puzzle game but designed to address a practical design problem. In other words, a similar virtual environment can be designed to address a practical design problem if the analogy between a game and the design problem exists (e.g., the analogy between protein structure and a puzzle game is used (Khatib et al., Reference Khatib, Cooper, Tyka, Xu, Makedon, Popović, Baker and Players2011)). In the rest of this section, each component of the MasonTris environment is explained.
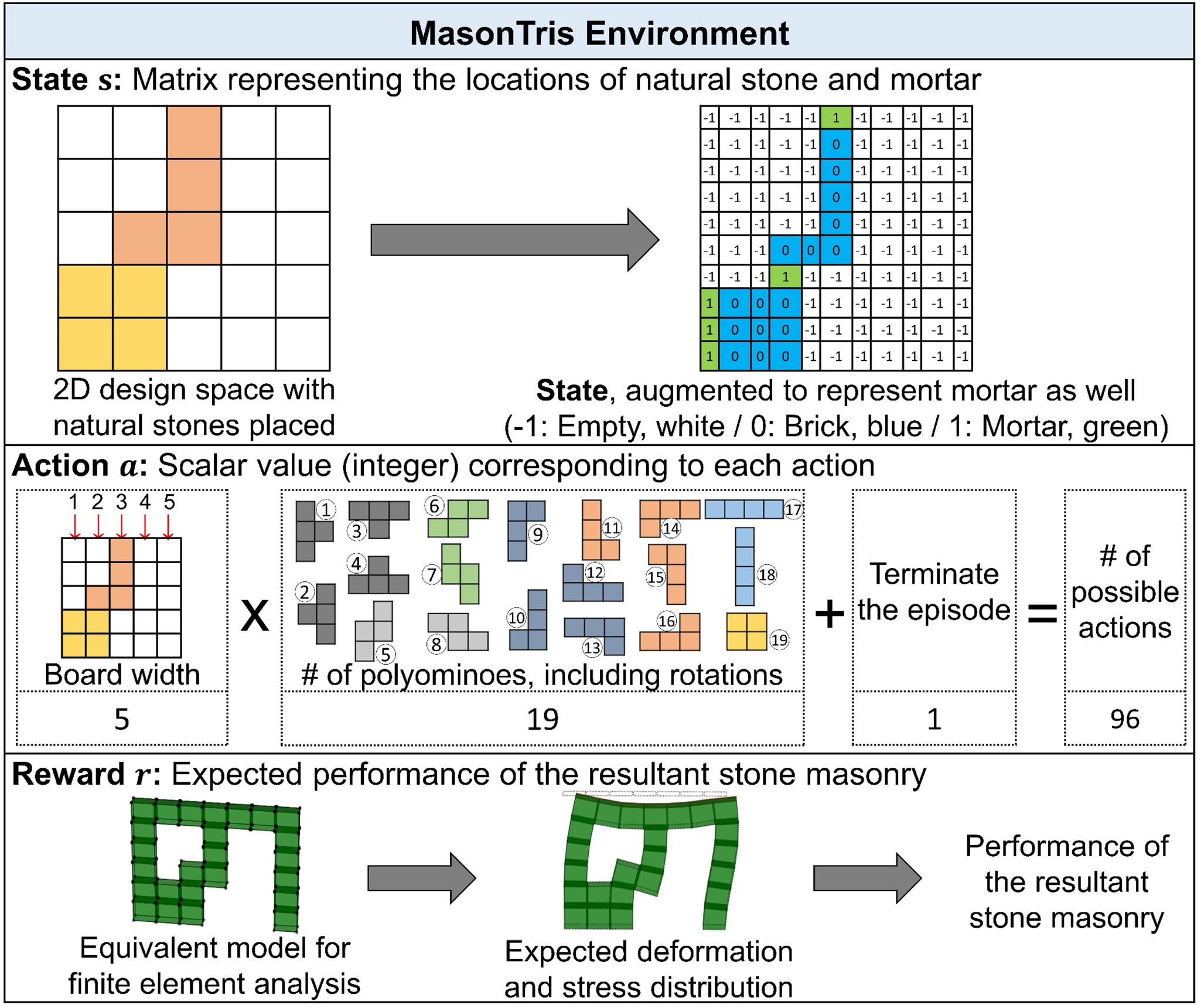
Figure 5. An overview of MasonTris environment illustrating state, action, and reward for RL.
Representation of states
In MasonTris environment, state s is defined as a 2D matrix derived from a board. Figure 5 shows an example of a state derived from a 5 × 5 board with 2 tetrominoes (i.e., natural stones) placed. It is shown that a board is augmented to a state, such that it can represent the mortar between the natural stones as well as the mortar between the natural stones and the outer shell. As a result, a board of size w × h yields a state of size (2w + 1) × 2h, since mortar is not applied between the natural stones and the ground. Each entity of the state has the value corresponding to its occupancy: empty (−1), natural stone (0), or mortar (1). This design choice ensures the following. First, the state can explicitly classify different types of materials (i.e., stone and mortar). By assigning empty space and mortar the value with a higher magnitude, the agent can focus more on the location of empty space and mortar, which plays an important role in the overall performance of the stone masonry. Second, by assigning 0 to natural stone, the outside of the design space (i.e., the outer shell) is also assumed to be made of natural stone. This is due to the typical behavior of DNNs (especially convolutional neural networks) (Abadi et al., Reference Abadi, Agarwal, Barham, Brevdo, Chen, Citro, Corrado, Davis, Dean, Devin, Ghemawat, Goodfellow, Harp, Irving, Isard, Jozefowicz, Jia, Kaiser, Kudlur, Levenberg, Mané, Schuster, Monga, Moore, Murray, Olah, Shlens, Steiner, Sutskever, Talwar, Tucker, Vanhoucke, Vasudevan, Viégas, Vinyals, Warden, Wattenberg, Wicke, Yu and Zheng2015), which regards that the value outside of the input matrix is zero (called “zero-padding”).
Representation of actions
In MasonTris environment, action a is defined as a scalar value (integer) representing possible actions, and its value ranges from 0 to a max. Here, the number of possible actions is identified by multiplying the board width and the number of available polyominoes (assuming an infinite supply to each polyomino), and then adding one additional action representing “terminate the episode and calculate reward”. When the number of available polyominoes is counted, rotated variants of each polyomino (e.g., ①–④ of Fig. 5) are assumed to be different from each other. In other words, action a can be regarded as a categorical value, where the value is assigned based on (1) the x-coordinate where a polyomino is dropped, (2) the type of polyomino to be dropped, and (3) whether the agent terminates the episode or not. For example, for a 5 × 5 board using tetrominoes, the number of possible actions is 96, which is derived by (5 × 19) +1, as shown in Figure 5, thus action a spans from 0 to 95. It should be noted that some of the actions might be infeasible, when there is no space to place the corresponding polyomino or when it is not desired in masonry (e.g., inserting a brick into a closed slot involves additional efforts, thus is not desired). To prevent such infeasible actions from being chosen, the proposed framework calculates and applies a feasibility mask for the action, which is a vector of binary values corresponding to actions. The agent only chooses from the actions where corresponding values in the feasibility mask are one.
Calculation of reward
In MasonTris environment, reward r is defined as a scalar value representing the expected performance of a stone masonry design. First, once the last action “terminate the episode and calculate reward” is chosen, the current 2D board (i.e., terminal state) is converted into the equivalent FEA model. Here, each coordinate of state s is regarded as a standard eight-node brick element, thus each polyomino and mortar gap is composed of multiple brick elements connected each other. Then OpenSeesPy (Zhu et al., Reference Zhu, McKenna and Scott2018) is used to evaluate the deformation and stress distribution. Based on this analysis, the performance of the equivalent stone masonry is calculated to provide the reward. It should be noted that a reward is provided only when an episode terminates, which means that intermediate states do not provide rewards. In other words, the policy of an agent also involves whether it should continue placing additional natural stones for higher reward or it should terminate the episode to retrieve the reward at the current time step.
Computational structural analysis: Structural analysis is performed to evaluate stone masonry designs assuming that the natural stones and mortar are made of elastic isotropic materials. To facilitate the structural analysis, the boundary conditions are applied such that the translations of all nodes at the ground level are not allowed (i.e., “pin-connected”), as shown in Figure 3. It should be noted that even though the input board is 2D, the FEA model is 3D considering the depth of the brick elements. In this paper, the gravitational load, friction force, and self-weight of stone masonry are not incorporated. Given the aforementioned configuration, the structural analysis evaluates the deformation (as shown in Fig. 5, where the degree of deformation is exaggerated for visualization) and the distribution of stress across the stone masonry design (as shown in Fig. 6). Then the distribution of principal stresses is derived to determine if any natural stones or mortar joints are subject to failure. The failure of material can be identified via the maximum-stress criterion. In this paper, the computational structural analysis tool called OpenSeesPy (Zhu et al., Reference Zhu, McKenna and Scott2018) is used. With a slight modification, the framework can perform more sophisticated analysis of masonry structures, as OpenSeesPy supports a wide variety of elements for finite element analysis (FEA) (e.g., truss, joint, interface) and material models [e.g., Drucker–Prager yield criterion (Drucker and Prager, Reference Drucker and Prager1952)].

Figure 6. The distribution of stress (z-direction) across the stone masonry design in Figure 5.
Safety factor: To evaluate the relative strength of different stone masonry designs, the proposed framework evaluates their safety factor, denoted as sf. Here, the safety factor represents how much stronger a structure is than it needs to be for an intended load (i.e., how much margin does it has). Typically, it is defined as the minimum ratio of maximum allowable strength to the calculated load across each element. For example, if a vertical stress of 10 MPa is applied on top of a structure (i.e., the typical amount of stress during the service of the structure), and the maximum allowable vertical stress of the structure is 20 MPa, then the resultant safety factor is 2. In this paper, the safety factor sf of a structure, with elements indexed with i, is defined as Eq. (4) where σ s,i and σ c,i are tensile strength (positive, if nonzero) and compressive strength (negative) of i-th element respectively, and σ p1,i and σ p2,i are maximum principal stress and minimum principal stress of i-th element. In other words, the minimum safety factor across all the elements, considering both tensile and compressive stress, is used as the safety factor of an overall stone masonry design. It should be noted that different elements may have different σ s,i and σ c,i, since a stone masonry consists of heterogeneous materials (i.e., natural stones and mortar).
 $$sf = \min _i\left\{{\matrix{ {\mathop {\min }\limits_{} \left({\displaystyle{{\sigma_{s, i}} \over {\sigma_{\,p1, i}}}, \;\displaystyle{{\sigma_{c, i}} \over {\sigma_{\,p2, i}}}} \right), \;} \hfill & {{\rm if}\;\sigma_{\,p1, i} \ge 0 > \sigma_{\,p2, i}\;{\rm or}\;\sigma_{\,p1, i} > 0 \ge \sigma_{\,p2, i}} \hfill \cr {\sigma_{s, i}/\sigma_{\,p1, i}, \;} \hfill & {{\rm if\;}\sigma_{\,p2, i} > 0} \hfill \cr {\sigma_{c, i}/\sigma_{\,p2, i}, \;} \hfill & {{\rm if\;}\sigma_{\,p1, i} < 0\;{\rm or}\;\sigma_{s, i} = 0\;} \hfill \cr {\infty , \;} \hfill & {{\rm if\;}\sigma_{\,p1, i} = \sigma_{\,p2, i} = 0} \hfill \cr } } \right.$$
$$sf = \min _i\left\{{\matrix{ {\mathop {\min }\limits_{} \left({\displaystyle{{\sigma_{s, i}} \over {\sigma_{\,p1, i}}}, \;\displaystyle{{\sigma_{c, i}} \over {\sigma_{\,p2, i}}}} \right), \;} \hfill & {{\rm if}\;\sigma_{\,p1, i} \ge 0 > \sigma_{\,p2, i}\;{\rm or}\;\sigma_{\,p1, i} > 0 \ge \sigma_{\,p2, i}} \hfill \cr {\sigma_{s, i}/\sigma_{\,p1, i}, \;} \hfill & {{\rm if\;}\sigma_{\,p2, i} > 0} \hfill \cr {\sigma_{c, i}/\sigma_{\,p2, i}, \;} \hfill & {{\rm if\;}\sigma_{\,p1, i} < 0\;{\rm or}\;\sigma_{s, i} = 0\;} \hfill \cr {\infty , \;} \hfill & {{\rm if\;}\sigma_{\,p1, i} = \sigma_{\,p2, i} = 0} \hfill \cr } } \right.$$Derivation of reward: Given the structural analysis results, the final reward is derived to grade stone masonry designs. The proposed framework explores the optimal design with DDQN, aiming at maximizing the reward. In other words, the formulation of reward can be regarded as an objective function of an optimization (maximization) problem. In this paper, the reward is designed to identify the optimal design satisfying the following conditions:
• The optimal design is the lightest feasible design, where feasible designs have the safety factors higher than a pre-defined threshold. In other words, a lighter feasible design should always have a higher reward. The weight of stone masonry is calculated by counting the number of coordinates occupied by natural stones in the design space (e.g., a tetromino is regarded to occupy four coordinates) for the outer shell and internal structure. It should be noted that the weight of the mortar is not counted.
• The design with a higher safety factor has a higher reward, in the case of ties for the lightest feasible design.
• The reward is bounded between −1 and 10, since a DQN agent cannot learn well if the magnitude of the reward is too low (does negligible update the parameters) or too high (neural network can be unstable). Here, the magnitude of the upper boundary is higher than that of the lower boundary to encourage the DDQN agent to explore positive rewards. The boundary is manually determined based on the observations of the loss function of the DNN during the development of the framework.
To satisfy the conditions, the reward is derived as Eq. (5) where m is the weight of the overall stone masonry, sf is the safety factor of the stone masonry, sf th is the threshold of safety factor to identify if a stone masonry is feasible or not, and m max and sf max are the upper limits of m and sf derived by assuming that the stone masonry is made of a complete solid natural stone (i.e., the internal structure is fully occupied with natural stones).
 $$\eqalign{& r = \left\{{\matrix{ {\displaystyle{{10} \over {m_{max} + 1}}\left[{m_{max}-m + \displaystyle{{sf-sf_{th}} \over {sf_{max}}}} \right], \;} \hfill \cr {\displaystyle{1 \over {sf_{max}}}( {sf-sf_{th}} ) , \;\;\;\;} \hfill \cr {-1, \;} \hfill \cr } } \right. \cr &\qquad\qquad\qquad {\rm if}\;sf > sf_{th} \cr &\qquad\qquad\qquad {\rm else\;if}\;sf_{th} > sf > sf_{th}-1 \cr &\qquad\qquad\qquad {\rm otherwise}\;( {sf \le sf_{th}-1\;{\rm or}\;OpenSeesPy{\rm \;fails}} ) } $$
$$\eqalign{& r = \left\{{\matrix{ {\displaystyle{{10} \over {m_{max} + 1}}\left[{m_{max}-m + \displaystyle{{sf-sf_{th}} \over {sf_{max}}}} \right], \;} \hfill \cr {\displaystyle{1 \over {sf_{max}}}( {sf-sf_{th}} ) , \;\;\;\;} \hfill \cr {-1, \;} \hfill \cr } } \right. \cr &\qquad\qquad\qquad {\rm if}\;sf > sf_{th} \cr &\qquad\qquad\qquad {\rm else\;if}\;sf_{th} > sf > sf_{th}-1 \cr &\qquad\qquad\qquad {\rm otherwise}\;( {sf \le sf_{th}-1\;{\rm or}\;OpenSeesPy{\rm \;fails}} ) } $$Figure 7 illustrates the calculation and scaling procedure of positive rewards [i.e., when sf > sf th in Eq. (5)]. First, r mass is calculated to evaluate the contribution of the weight m to the reward. Since m is the number of coordinates occupied with natural stone, r mass has a discrete integer value ranging from 0 to m max. Then r sf is calculated to evaluate the contribution of the safety factor to the reward. r sf has a continuous value ranging from 0 to 1, as sf − sf th is divided by sf max, which is the upper limit of the magnitude of sf. Bounding r sf between 0 and 1 ensures that a lighter feasible design always has a higher reward, regardless of the difference in safety factor. Lastly, the final positive reward r + is derived by dividing the sum of r mass and r sf by 10/(m max + 1). This ensures the positive reward to be bounded by 10.

Figure 7. The calculation and scaling procedure of positive rewards yielding a bounded reward.
Design exploration via DDQN
The proposed framework adopts DDQN, where its DNN architecture and design exploration strategy are tuned to solve MasonTris problems. In this section, the details on the DNN and exploration strategy are presented.
Deep neural network architecture
In stone masonry design, the spatial correlation among empty space, natural stones, and mortar is important. To capture such spatial correlation, the proposed framework adopts a convolutional neural network (CNN) (LeCun et al., Reference LeCun, Bengio and Hinton2015), which can capture spatial correlations from 2D/3D data, as a part of the neural network approximating action-value function. Figure 8 shows the DNN architecture used in this paper, which includes three convolutional layers followed by two fully connected layers. It is shown that the 2D convolution kernels sweep the input data (i.e., state s) to learn spatial features, and the fully connected layers to derive the action-value function for each action based on the spatial features. Here, the number of layers and the number of hidden nodes in each layer are manually tuned based on the observation during the framework development. The hyperparameters (e.g., kernel size, hidden node size, etc.) can be adjusted depending on the complexity of the problem (e.g., the size of the board). For example, the hidden node size can be increased when the board size increases, or additional workpieces are allowed (i.e., the number of available action increases).

Figure 8. The DNN architecture to approximate action-value function ![]() $Q_\theta ^\ast ( {s, \;a} )$.
$Q_\theta ^\ast ( {s, \;a} )$.
Design exploration strategy
Typically, a DQN agent adopts an ɛ-greedy policy with ɛ decaying from a large value to a small value. In other words, the agent initially focuses on exploration and then gradually focuses more on exploitation later. While this approach provides reasonable results for many standard environments, it is observed that this approach may lead to the scarcity of positive rewards due to the following characteristics of MasonTris problem:
(1) In case the safety factor threshold is high, there are only a few feasible designs providing positive rewards. Therefore, it is difficult to locate a feasible design with an ɛ-greedy policy due to the random action chosen at each time step.
(2) For a large design space, even selecting a few random actions in the middle of the design may yield a completely different result, while the standard ɛ-greedy policy is intended to provide a sequence of action slightly deviated from the current best one to balance between exploration and exploitation. In other words, the agent could not exploit well based on the current state. This makes it difficult for the agent to locate the designs with positive rewards, which are already sparse in the design space.
The scarcity of positive rewards can significantly slow down the training process, since the update of the DNN parameters θ is guided to maximize the expected reward achieved by the agent. In other words, if no positive reward is provided, the agent can only learn “how to avoid the lowest negative rewards” rather than “how to achieve a positive reward”, since none of the actions will yield a positive action-value function ![]() $Q_\theta ( {s, \;a} )$.
$Q_\theta ( {s, \;a} )$.
To address the issue, the framework jointly utilizes additional exploration strategies, called almost-greedy policy, complementing the standard ɛ-greedy policy. Almost-greedy policy is an ɛ-greedy policy with a small constant value of ɛ, such that at most only one action is randomly chosen on average during an episode. In other words, ɛ equals to one divided by the theoretically maximum length of an episode, which is driven by dividing the minimum size of polyominoes with the number of coordinates in a board. For example, ɛ equals 0.16 = 4/(5 × 5) when a 5 × 5 board and tetrominoes are used (for the environment in Fig. 5). By occasionally adopting almost-greedy policy for some of the RL iterations, the framework better exploits the current policy, thus more likely to locate a design with a positive reward earlier to speed up the training process. The proposed design exploration strategy via the joint utilization of regular ɛ-greedy and almost-greedy policy can be applied to solve any design problems, where only few feasible solutions exist across a broad design space.
On-demand calculation of rewards for efficient parallelization
A typical RL framework calculates the reward during the exploration, such that the reward values are stored in the experience replay as a part of experiences. However, for the motivating example, calculation of reward (i.e., FEA for structural analysis) is computationally the most expensive part of exploration, where the calculation time significantly varies depending on the topological structures (i.e., some design requires small computation time while others may require significantly more time). For example, during the development of MasonTris in 10 × 20 board, it is observed that the evaluation of a complex design candidate takes 20+ s while the evaluation of a simple design candidate takes 2 s. Therefore, when multiple exploration sessions are simultaneously running, the efficiency of the exploration is limited by the session involving the most time-consuming calculation. Considering the number of design candidates to be evaluated (10,000+ for even a simple design problem), it can be a significant bottleneck in more realistic applications, as the evaluation time roughly scales with the size of the board and will dramatically increase when the framework is extended to 3D design problem.
To address the issue and allow efficient parallelization, the proposed framework has a component called trainer, which intervenes across the MasonTris environment, experience replay, and DDQN agent as follows. First, MasonTris environment does not calculate reward during the exploration, but only provides the flag (0 for intermediate states and 1 for terminal states) to experience replay. When the random batches of sequential experiences are retrieved from the experience replay to train the agent, the trainer utilizes parallelized structural analysis module to calculate the rewards, only when the retrieved rewards are 1's. Second, for efficient calculation of rewards, the trainer utilizes parallel workers of structural analysis module with Dask (Rocklin, Reference Rocklin2015), which is a Python library for efficient parallel computation. This allows queuing the calculation of rewards, such that calculations are simultaneously done with multiple workers without bottleneck as shown in Figure 4 (bottom-right). Third, as the actual rewards are not explicitly stored in the experience replay, the trainer does book-keeping of state-reward pair, such that it can re-use the reward without calculation, if the same state is explored in the future. This ensures the efficiency of the proposed framework by preventing redundant calculations. The proposed practical modification can improve the efficiency of any RL framework utilizing experience replay (e.g., DQN and DDQN), especially when the evaluation of rewards is computationally costly.
Experiments
Experimental settings
In this section, the feasibility of the proposed framework is validated by solving MasonTris problems. Specifically, the initial experiment is performed where the scale of the design space is the same as Tetris (i.e., design space is 10×20 board, and tetrominoes are used). Figure 9 illustrates the MasonTris problem for the experiment where the vertical pressure (P) of 1 MPa and the safety factor threshold (sf th) of 2 are applied. In addition, the properties of natural stone and mortar are configured as close as the actual masonry to provide realistic results based on the Internet resources and academic papers (Mohamed and Djamila, Reference Mohamed and Djamila2018; Schiavi et al., Reference Schiavi, Cellai, Secchi, Brocchi, Grazzini, Prato and Mazzoleni2019). The dimensions and material properties used for structural analysis are provided in the Appendix (Table A1).
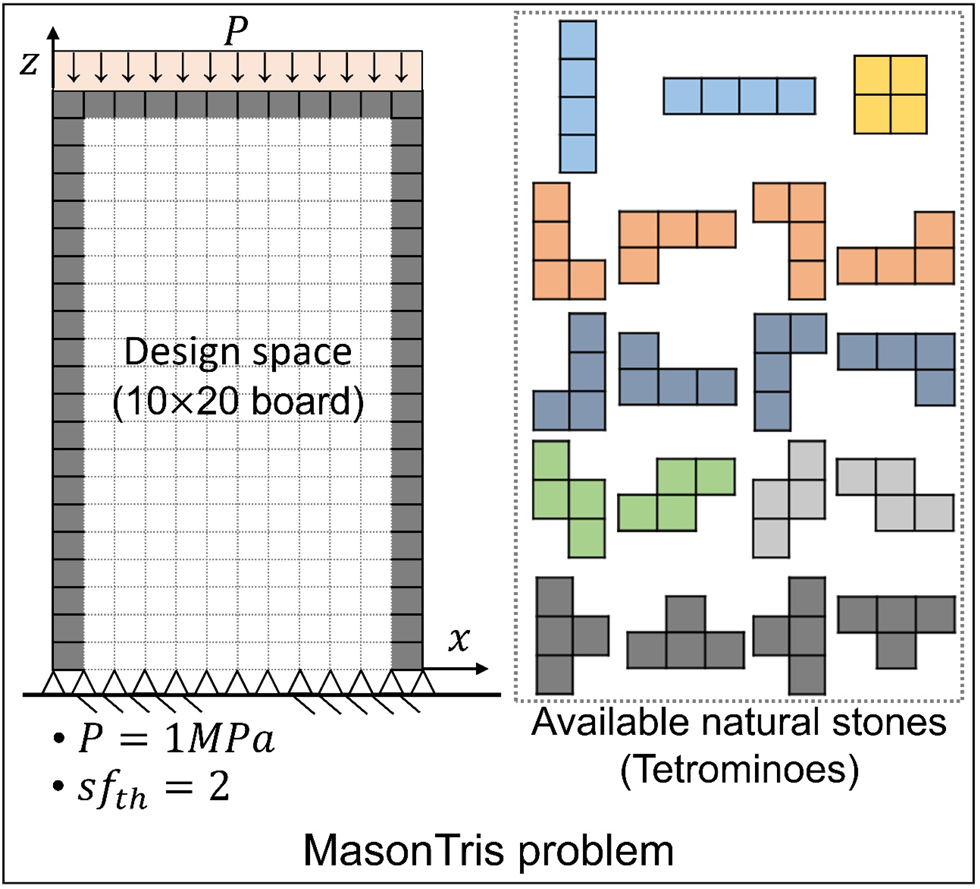
Figure 9. MasonTris problem for the initial experiment.
Given the aforementioned configuration, the proposed framework is used to learn stone masonry design policy under a high-performance computing resource based on AMD-EPYC CPU with 18 cores and 128 GB RAM assigned for each run. The configuration of tuning parameters for DDQN is provided in the Appendix (Table A2).
Results and observation
The performance of the framework is measured by periodically evaluating the reward obtained by the agent assuming the agent follows greedy policy [Eq. (1)]. Figure 10 shows the behavior of the reward achieved by a single agent. It is shown that the agent gradually but non-monotonically achieves higher rewards as it learns design policy. Also, the performance of the agent sometimes significantly drops, which typically happens when the transition from a local optimum to another local optimum happens.

Figure 10. An example of the result from a single agent, and the average rewards obtained from eight repetitions with/without almost-greedy policy.
To demonstrate the effectiveness of adopting the proposed almost-greedy policy, the performances with/without almost-greedy policy are compared. Figure 10 also shows the results based on eight repetitions per case. In each iteration, the baseline only adopts standard exploration, while the baseline + almost-greedy policy adopts standard exploration with 80% and almost-greedy exploration with 20%. For the almost-greedy policy, ɛ of 0.02 is chosen. This is to ensure that the expected number of random actions is at most one, as the maximum number of actions in an episode is 50 in the target problem. It is shown that adopting the proposed almost-greedy exploration helps the agent achieve higher rewards much faster than the baseline.
Figure 11 shows the progression of stone masonry design as the agents improve their policies (eight agents are simultaneously trained for 24 h). To illustrate the overall progression of the agents (i.e., not affected by temporary policy transitions of some agents), the values above 25th percentiles are used to generate Figure 11. The central red line indicates the average reward, and the shaded area indicates the range of minimum/maximum rewards obtained by the top 75% of the agents. It is observed that the agents try different design geometries and gradually derive lighter structures with maintaining their safety factors above 2. As the training goes on, the resultant design converges to the design with a thin single column with capital on top (similar to human designed columns), having a reward of around 6.96. The global optimal design has not been confirmed via brute-force search as it takes too much time. However, as the design with a single thin center column without capital (i.e., using five straight bars) does not satisfy the safety constraint (sf ≈ 1.6), the resultant design is expected to be the global optimal design. The results indicate that the proposed framework could address the research question by learning effective stone masonry design policy, similar to what is actually designed by human, without prescribed knowledge.

Figure 11. The progression of stone masonry design under the proposed framework for the design problem is shown in Figure 9 (eight agents are simultaneously trained for 24 h).
Adaptability of the framework and discussion
To demonstrate the adaptability of the proposed framework, a slightly more complex MasonTris problem is tested, which is shown in Figure 12 (left), with mostly the same parameters used (Table A1 and Table A2 in the Appendix). For this MasonTris problem, the design space is wider (i.e., 20×10 board), additional polynominoes are allowed (i.e., including dominoes, trominoes, and tetrominoes), and lateral pressure P L is applied to the left side of the top of the outer shell. This problem is much more complex than the initial problem with respect to RL, since it has a larger number of actions (190 versus 540) and initial conditions (i.e., the horizontal location of the initial block). To address the challenge, the number of hidden nodes in the DNN has been increased to learn more complex action-value function (Table A2 in the Appendix). With respect to stone masonry design, this problem represents a realistic approximation of an actual stone masonry problem for the following reasons:
• 20 × 10 board has a large number of states, about 7 × 2200 (Algorta and Şimşek, Reference Algorta and Şimşek2019). Assuming that the evaluation of each state requires FEA and the distribution of the reward across the design space is not smooth, it is extremely time-consuming to identify an effective design policy without prescribed knowledge in stone masonry design.
• The problem utilizes heterogeneous units of different sizes to represent a stone masonry design problem. Considering the rotation of polyominoes, 27 heterogeneous shapes are used, making this problem more challenging.
• Combination of vertical pressure (representing the load on top of the masonry structure) and lateral pressure (representing the load from lateral ground movement) is applied. It is a realistic configuration to test the typical failure modes of masonry under in-plane seismic loads (Oyguc and Oyguc, Reference Oyguc and Oyguc2017).

Figure 12. A more complex stone masonry design problem (left) and the progression of stone masonry design under the proposed framework (right, 20 agents are simultaneously trained for 96 h)
Figure 12 (right) shows the progression of the stone masonry design under the proposed framework, where 20 agents are simultaneously trained for 96 h and the values above 25th percentile are used to generate the plot. Similar to the initial experiment, it is observed that the agents gradually derive lighter designs with safety factors above 2. However, as this MasonTris problem involves more complex external excitation, it is shown that the agents took more time to design complex design geometries, gradually forming more and larger cavities in the structure. Another notable feature is that the agent jointly utilizes dominoes/trominoes/tetrominoes in order to form arch-like patterns, to respond to the vertical and lateral load. The resultant design has several columns with cavities within them, in addition to the capital on top of some of the columns. The columns are slightly diagonal to counter the lateral load and vertical pressure at the same time. In the meantime, the final design has two long horizontal components sticking to the ceiling, which may not be feasible in actual stone masonry where the self-weight of natural stones is incorporated (i.e., should be replaced with shorter horizontal components to make sure they do not fall). While it does not violate the simplified environments, such practical design considerations, similar to the orientation constraints used in the previous works (Whiting et al., Reference Whiting, Shin, Wang, Ochsendorf and Durand2012), can be incorporated into the creation of feasibility masks to prevent infeasible designs when the framework is applied to actual design problems. Also, it is confirmed that the two blue and orange T-shaped components at the bottom of the final design can be replaced with straight elements to improve reward value (i.e., the bumps of the column can be removed). Such redundancy of design is expected to be present as the AI agent was not sure at the beginning of the design whether the column is going to be a part of an arch pattern or not. The aforementioned observations indicate that the final design is not the global optimal design yet, and there might be still a better design. In this problem, it is impossible to confirm a global optimal design via brute-force search, as it takes too much time. However, the results justify the adaptability of the proposed framework to more complex stone masonry design problems, such that it can continuously improve design policy to address practical design problems, gradually approaching the global optimal design.
Based on the results, future research direction lies in investigating the computational scalability with different board sizes (i.e., different numbers of nodes and elements for FEA). Another direction lies in the use of pre-trained models through transfer learning (Torrey and Shavlik, Reference Torrey and Shavlik2010) or curriculum learning (Bengio et al., Reference Bengio, Louradour, Collobert and Weston2009). The core concept of curriculum learning lies in providing gradually more difficult problems to the agent similar to the way that a curriculum for a student is designed. For the stone masonry design problem, the safety factor threshold can be gradually increased to allow the agent to learn from an easier problem (small safety factor threshold) to a more difficult problem (high safety factor threshold). Adoption of curriculum learning for autonomous parameter tuning will be an interesting direction, as the experimental results indicate that the DNN architecture needs to be tuned based on the scale/complexity of the target problem.
Conclusion
In this paper, an RL-based stone masonry design framework is proposed, which can learn stone masonry design policies from virtual experiences in MasonTris environment. The feasibility and adaptability are demonstrated in a simplified version of stone masonry problems, called MasonTris problems. It is shown that the framework autonomously improves its design policy via DDQN, guided by the physical interpretation of different structures with computational structural analysis. The proposed framework can efficiently learn effective design patterns (e.g., columns with capital on top, arch-like patterns, and forming cavities inside the structure) without prescribed knowledge, otherwise takes a huge amount of time via exhaustive exploration.
This paper presents the first step in developing an innovative framework to address stone masonry design problem. While the current framework is not tested in an actual stone masonry design problem, it demonstrated its capability to autonomously improve its design policy using heterogeneous sizes/shapes of masonry units, thus the framework can be applied to practical stone masonry design problems upon improving the scalability of the framework and incorporating more realistic assumptions. For example, increasing the board size and the resolution of workpieces will allow representing more realistic pixelated natural stones. The framework can contribute to addressing an important challenge in stone masonry design, which is the high dependence on domain experts and/or prescribed domain knowledge.
On top of its potential to address the important challenges in stone masonry design problems, the proposed methodology has meaningful contributions to the relevant research fields. First, in terms of TO, the proposed RL framework allows the optimization of topological structures consisting of heterogeneous design units, where typical TO methods are not effective. Therefore, the proposed work can be generalized to open opportunities in design automation for sustainability, as the use of locally available natural and recycled feedstock involves similar design challenges (i.e., stochasticity and heterogeneity in nature). For example, the proposed RL framework can be applied to mass timber construction design, a promising way to reduce carbon emission in construction, which should address the inherent variability of wood products. Second, in terms of RL, the proposed RL framework provides a practical modification of on-demand reward evaluation, to address the bottleneck involving the evaluation of rewards. This will promote the use of RL to solve various practical engineering problems involving time-consuming computer simulations (e.g., fluid flow design). Lastly, in terms of design, the proposed RL framework is a meaningful case study utilizing a gaming AI environment to solve a practical design problem without prescribed knowledge. The proposed framework can be applied to a wide variety of domains, readily available in different practical scenarios. For example, similar to the way that game players contributed to the discovery of protein structure (Khatib et al., Reference Khatib, Cooper, Tyka, Xu, Makedon, Popović, Baker and Players2011), the proposed framework can be extended to a different practical design problem based on the analogy between a game and the design problem. The following future investigations can contribute to the further improvement of the framework, leading to its acceptance in a practical scenario.
Incorporating stochastic natures of natural stones: Stone masonry utilizing local natural stones is a sustainable option for construction, but involves stochastic availability of workpieces as well as stochastic material property. Incorporating such stochastic natures (i.e., making MasonTris a stochastic environment) will be a further step for the framework to address and represent actual stone masonry design problem.
Extension to different design problems: The proposed framework demonstrated different variants of column-type designs under the design problem where vertical pressure is the major component of external forces. However, the framework will be able to derive completely different types of designs under different design problems (e.g., designing a structure withstanding horizontal hydrostatic pressure). Therefore, extension to different design problems will be one of the future works to validate the generalizability of the proposed framework.
Approximating FEA for faster learning: As the current framework utilizes time-consuming FEA to evaluate each design candidate, it may not be feasible to evaluate a number of possible designs in a larger-scaled practical problem. It is an important barrier to applying the proposed method to a practical problem, as the computation time of FEA significantly increases as the board size increases. To address the challenge, simultaneously training a surrogate model of FEA for faster evaluation of design candidates can be a future direction to speed up the training. This will allow the proposed framework to incorporate more realistic settings (e.g., self-weight, friction force, more sophisticated material models) representing actual stone masonry design.
Extraction of domain knowledge and incorporation in the future design: The scope of this manuscript is to introduce an RL-based design automation framework without prescribed knowledge, as the knowledge on stone masonry design has been waning (i.e., there is not enough knowledge that can be jointly used with data-driven or other ML methods). However, one of the promising research directions in the RL research community is called model-based RL, which aims at incorporating existing domain knowledge to guide the AI agents. Aligned with this research direction, future works include (1) the extraction of generalizable domain knowledge on stone masonry design based on the experience of AI agents and (2) the incorporation of extracted domain knowledge to guide AI agents in different scenarios.
Acknowledgements
The authors acknowledge the support of the Experiential AI Postdoc Fellowship program from Northeastern University and Roux AI Institute.
Conflict of interest
The authors have no conflicts of interest to declare.
SungKu Kang received the B.S. degree in Mechanical and Aerospace Engineering from Seoul National University in 2012 and the Ph.D. in Mechanical Engineering from University of Illinois Urbana-Champaign in 2017. He is currently a Postdoctoral Research Fellow of Civil and Environmental Engineering with Northeastern University, Boston, MA, USA, as a part of Experiential AI Postdoc Scholarship program. Prior to joining Northeastern University, he worked as a Postdoctoral Research Associate at the Department of Industrial and Systems Engineering at Virginia Tech, where he studied the integration between design rules and data-driven methods for efficient engineering design. His research interests include the use of implicit domain knowledge and machine learning techniques, especially reinforcement learning, for design automation of products, architectural structures, and infrastructures, incorporating sustainability and personalization in mind. He envisions delivering a holistic methodology for design automation in general, where the scope of design also includes but is not limited to: material design and service design.
Jennifer G. Dy is a Full Professor at the Department of Electrical and Computer Engineering, Northeastern University, Boston, MA, where she first joined the faculty in 2002. She received her M.S. and Ph.D. in 1997 and 2001, respectively, from the School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN, and her B.S. degree from the Department of Electrical Engineering, University of the Philippines, in 1993. Her research spans both foundations in machine learning and its application to biomedical imaging, health, science, and engineering, with research contributions in unsupervised learning, interpretable models, explainable AI, continual learning, dimensionality reduction, feature selection/sparse methods, learning from uncertain experts, active learning, Bayesian models, and deep representation learning. She is Director of AI Faculty at the Institute for Experiential AI, Director of the Machine Learning Lab and is a founding faculty member of the SPIRAL (Signal Processing, Imaging, Reasoning, and Learning) Center at Northeastern. She received an NSF Career award in 2004. She has served or is serving as Secretary for the ICML Board (formerly, International Machine Learning Society), associate editor/editorial board member for the Journal of Machine Learning Research, Machine Learning Journal, IEEE Transactions on Pattern Analysis and Machine Intelligence, organizing and/or technical program committee member for premier conferences in machine learning, AI, and data mining (ICML, NeurIPS, ACM SIGKDD, AAAI, IJCAI, UAI, AISTATS,ICLR, SIAM SDM), Program Chair for SIAM SDM 2013, ICML 2018, AISTATS 2023, and AAAI 2024.
Michael B. Kane received the B.S. degree in Architectural Engineering and the M.S. degree in Civil Engineering from Drexel University, Philadelphia, PA, USA, in 2009 and 2009, respectively, and the M.S. degree in Electrical Engineering and the Ph.D. degree in Civil Engineering from the University of Michigan, Ann Arbor, MI, USA, in 2011 and 2014, respectively. He is currently an Assistant Professor of Civil and Environmental Engineering with Northeastern University, Boston, MA, USA. Prior to joining Northeastern, he worked as a fellow at the U.S. Department of Energy's Advanced Research Project Agency-Energy (ARPA-E), where he identified new technology development opportunities for control of civil energy infrastructure, primarily in the areas of transportation, buildings, and distributed energy resources. His research and teaching focus on automation in the built environment and how people interact with automated systems. In 2021, he received the NSF CAREER award. Dr. Kane is a member of the American Society of Heating, Refrigeration, and Air-conditioning Engineers (ASHRAE) and of the Institute of Electrical and Electronics Engineers (IEEE). He is a member of the IEEE Smart Buildings-Loads-Customer (SBLC) Systems Technical Committee. He is a Senior Member of the American Society of Civil Engineers (ASCE). He is an Engineer in Training in the State of Pennsylvania.




















