An approach to human–machine collaboration in innovation

Abstract

If a solvable problem is currently unsolved, then something important to a solution is most likely being overlooked. From this simple observation we derive the obscure features hypothesis: every innovative solution is built upon at least one commonly overlooked or new (i.e., obscure) feature of the problem. By using a new definition of a feature as an effect of an interaction, we are able to accomplish five things. First, we are able to determine where features come from and how to search for new ones. Second, we are able to construct mathematical arguments that the set of features of an object is not computably enumerable. Third, we are able to characterize innovative problem solving as looking for a series of interactions that produce the desired effects (i.e., the goal). Fourth, we are able to construct a precise problem-solving grammar that is both human and machine friendly. Fifth, we are able to devise a visual and verbal problem-solving representation that both humans and computers can contribute to as they help counteract each other's problem-solving weaknesses. We show how computers can counter some of the known cognitive obstacles to innovation that humans have. We also briefly discuss ways in which humans can return the favor. We conclude that a promising process for innovative problem solving is a human–computer collaboration in which each partner assists the other in unearthing the obscure features of a problem.

1. INTRODUCTION

Artificial Intelligence, especially through the 1980s, attempted to get machines to perform many cognitive tasks on their own. For problem solving that required innovation, these attempts were mostly unsuccessful, with the possible but debatable exceptions of Lenat's work on AM and EURISKO (Lenat & Brown, 1984; Ritchie & Hanna, 1984). A new theory of cognitive innovation, the obscure features hypothesis (OFH), articulates a key foundation that all innovative solutions are built upon at least one obscure feature of the problem (McCaffrey, 2012). Based on a new definition of a feature of an object (i.e., specifically, an effect of an interaction between the object and other entities), we are able to demonstrate several results. We articulate the origin of features and a method to find new ones. We show that the set of features of an object is not computably enumerable. Because neither computer nor human can list out all features of an object, we move to devise a representation that is easy for both humans and computers to contribute to in ways that counter each other's weaknesses. The representation consists of a problem-solving grammar and visualization method that is both human and machine friendly. The overall result is a human–computer interface that produces a human–machine partnership that is potentially more innovative than either partner working alone.

2. THE OBSCURE FEATURES HYPOTHESIS FOR INNOVATIVE PROBLEM SOLVING

If a solvable problem is currently unsolved, something crucial to the solution is being overlooked. If a solvable problem has been unsolved by the problem-solving community for an extended period of time, then the something that is being overlooked is either infrequently noticed or never-before noticed (i.e., obscure). Further, we will call all somethings that can be either noticed or unnoticed features. Other authors use a variety of terms: attributes, properties, aspects, behaviors (Gero, 1990), resources (Altshuller, 1996), and relations. Based on this reasoning, the OFH, originally presented in McCaffrey (2012), can be stated as follows: all innovative solutions to a problem are built upon at least one obscure feature of the problem. The OFH approach leads to a systematic derivation of innovation-enhancing techniques by following these steps: articulate a wide panoply of possible types of features, disclose why humans tend to overlook certain features types, and construct techniques to help humans unearth the obscure members of these feature types.

In contrast to the OFH, previous psychological theories fall short of becoming systematic. The representation change view (Ohlsson, 1992; Knoblich et al., 1999) proposed that solving a problem that requires innovation necessitates a change in the problem's representation. These researchers, however, never specified an array of possible types of representation change, the cognitive inhibitions to noticing various representation changes, and techniques to uncover hidden representation changes. Similarly, the distant association view (Mednick, 1962) stated that solving problems requiring innovation involves leveraging an association that is semantically distant from the concepts of the problem. Followers of this approach never articulated a multitude of the types of associations, cognitive reasons why certain types of associations are overlooked, and techniques to help bring forth the overlooked elements of those types at the appropriate semantic distance.

In the engineering field, TRIZ, a theory of inventive problem solving (Altshuller, 1996), uses a category system of 39 types of features and a matrix of contradictions that occur when a solution needs to resolve an apparent conflict between the desired values of two of the features (e.g., faster acceleration in a car and better gas mileage; Rantanen & Domb, 2008). The matrix focused on techniques (i.e., principles, in the TRIZ vernacular) that could be used to try to overcome a contradiction and construct a solution that allowed both features to simultaneously reach their desired outcomes. Many tools have been developed under the TRIZ umbrella since its early days of focusing on contradictions between two features (Rantanen & Domb, 2008), but one commonality between OFH and early TRIZ is their focus on features. OFH creates techniques to unearth commonly overlooked features while early TRIZ crafted techniques to overcome contradictions that occur when the desired values of two features seem impossible to achieve simultaneously.

Finally, the core activity of finding obscure features of a problem bears some resemblance to the problem explored in machine intelligence of finding missing data, missing features, and missing values (Mitchell, 1997).

In the next section, we proceed to define a feature of an object as an effect of an interaction between the object and other entities. This definition permits us to do several things. First, it allows us to understand where features come from and develop a method to search for new features. Second, the definition permits rigorous arguments to be made on the nonenumerability of the set of features of an object. Third, it allows us to describe problem solving as searching for a sequence of interactions among objects that produce the effects articulated by the goal. Fourth, it allows us to create a problem-solving syntax and visualization method that is both human and machine friendly so that humans and computers can easily collaborate when problem solving together.

3. NIETZSCHE’S DEFINITION OF FEATURE

Building upon the philosopher Nietzsche, a feature of an object is the effect of an interaction of the object with other entities: objects, materials, energies (e.g., electrical), and forces (e.g., gravity). As Nietzsche states: “The features of a thing are effects on other ‘things’: if one removes other ‘things,’ then a thing has no features” (Nietzsche, 1901/1968). From this vantage point, no feature is intrinsic to the object, and consequently no feature remains the same in all circumstances. For example, mass and length are strong candidates for being intrinsic to the object and unchanged in all circumstances. Special relativity theory informs us, however, that as the speed of an object increases, its length contracts and its mass increases (Einstein, 1920/2004). Length and mass, seemingly strong candidates for being intrinsic, actually result from an interaction: in this case, an interaction between an object traveling a certain speed and a measuring device in a frame of reference. From more recent science news, there is another reason why mass may not be intrinsic. A particle's mass appears to be the result of an interaction between the particle and Higgs bosons (Ellis et al., 2015).

No feature of an object remains the same in all circumstances. An object's color certainly changes as circumstances change and is the result of an interaction among the object, light, the human eye, the visual cortex, and other things. Not even the existence of the object remains the same in all circumstances, because the object can be destroyed in some circumstances. In looser terms, a feature “does not belong” to the object but “belongs” to an interaction in which the object participates. We cannot know the object “in itself” but only what effects it produces during interactions.

Some interactions could be considered direct while others indirect. A distant star emits light, so detection of light by the human eye could be considered a direct interaction between the star and the human eye. Adding a telescope adds an intermediary in this chain of interactions and makes the interaction more indirect. Planets encircling distant stars do not emit light, so their detection needs to be even more indirect. Several ways have been devised, including the following method. When a planet travels between the star and the observing telescope, it blocks a tiny amount of starlight, and this variation can be detected (Mason, 2010). This slight variation in the starlight provides evidence of the presence of a planet. There are also several other methods that could be used to provide corroborating evidence of the planet's presence (Mason, 2010). In sum, these examples suggest that the difference between direct and indirect interactions is one of gradations and not a binary distinction. Further, these examples make clear that every effect of an interaction needs some kind of sensor to detect it (e.g., the human eye or a telescope).

Other approaches that are in line with Nietzsche's definition of feature include Suchman (1987), who argued that features are not abstract and universal but rather relative to agents and their situations.

The history of a feature's definition in the psychological and engineering literatures reveals definitions that remain vague. A review paper on the concept of a feature in the psychological literature used this definition: “any elementary property of a distal stimulus that is an element of cognition, an atom of psychological processing” (Schyns et al., 1998). This definition relies on an understanding of property, which is left undefined. Further, it assumes that a feature corresponds to some small unit of cognition. However, depending on the task at hand, humans switch what is elemental in their thinking. For a carpenter, a piece of wood might be the unit of conception. A physicist, however, might conceive of wood at a level of atoms, subatomic particles, subatomic strings, or other units that physicists may one day posit. Depending on the task, humans easily alter what is the unit of cognition. One moment we may conceive of an atom as a unity and then next moment as a multiplicity (i.e., a collection of subatomic particles). Further, this definition does not tell us where new features come from and, consequently, does not yield a method to unearth new features when we are trying to be innovative. Finally, this definition of a feature does not lead to quantification arguments about the number of possible features. For these reasons, we find the current definitions from the psychology literature to be unsatisfactory for the study of innovation.

A review paper on features in the engineering literature reveals that all definitions are some variation on the following: “information sets that refer to aspects of form or other attributes of a part” (Salomons et al., 1993). The unspecified notions of “form” and “attribute” in this definition leave it at a vague level. Further, this definition does not tell us where new features come from, how to uncover new features, or how to quantify the number of possible features.

In the upcoming sections, we will leverage our definition of feature to accomplish multiple things. First, our definition sheds light on where features come from and leads to a method to search for new features. This conclusion is important for innovation as innovative solutions are built upon commonly overlooked and new features (i.e., obscure). Second, it allows us to attempt to quantify an object's features and determine whether or not that set is computably enumerable. Third, it allows us to characterize problem solving as a search for a sequence of interactions among objects that satisfy the desired effects of the goal. Fourth, it results in a precise problem-solving grammar that is simultaneously human and machine friendly. Fifth, it makes possible a visual interface through which humans and computers can collaboratively innovate together; and where computers help counteract human weaknesses to uncovering obscure features and humans do the same for computers.

4. WHERE DO NEW FEATURES COME FROM?

The Nietzschian definition of a feature tells us where features come from. More important, it hints at where new features come from, which leads to a method to search for new features. If features come from interactions, then new features come from new interactions. Simply interact the object with things it has never interacted with before and see if new features emerge. Because innovative solutions are built upon obscure features (i.e., commonly overlooked as well as new features), having a way to look for new features is important for systematizing the invention process. Instead of relying on accident and serendipity, a more methodical approach of interacting together previously uninteracted things could produce new features and ultimately lead to new inventions on a more regular basis.

Science is replete with stories of new features of objects emerging after interacting the objects with things they have never interacted with before. Superconductivity in ceramics, for example, emerged from interacting a specific ceramic material with electricity at a near-absolute-zero temperature (van Delft & Kes, 2010). Superinsulation, the opposite of superconductivity, was accidentally discovered in 2008 by interacting a different ceramic material with electricity in similarly extreme temperature conditions (Vinokur et al., 2008).

The same principle works for common objects in less extreme conditions. Interacting a common object with other objects that it may have never interacted with before can produce new effects (i.e., features). If we interact a light plastic chair with a person in a canoe who has lost the oars, then the chair can become an oar (i.e., turn the chair upside down, grab a couple of legs, and start rowing). If we interact this same chair with a short delicate plant that cannot stand a great deal of direct sunlight, then the chair can become a source of shade for the plant. If we interact this chair with a pile of styrofoam pellets that we need to move, then by grabbing one chair handle with one hand and a chair leg with another hand we can begin to shovel the pellets out of the way. Creating an extensive list of objects for the plastic chair to interact with will likely produce new effects and thus new features of the chair.

5. NONENUMERABILITY OF AN OBJECT’S FEATURES

Given the definition of an object's features as the effects of interactions between the object and other entities, we will address the sizes of various sets: entities to interact with, interactions that the object can participate in, ways for two objects to interact, uses of a particular interaction involving the object, and ultimately features of an object.

Along this path of reasoning, we will show that the set of possible interactions that an object can participate in is not computably enumerable. However, even if this set were computably enumerable, this just means that a computer could list out the interactions so they could be explored for possible effects. We will also show that when examining a particular interaction, a computer might not be able to derive all of the effects of that interaction. Thus, even if the set of interactions were computably enumerable, the set of features still may not be.

We will consider an entity to be either an object, material, energy, or force. There is a fairly short list of forces (e.g., gravity) and types of energy (i.e., acoustic, biological, human, chemical, electrical, electromagnetic, hydraulic, magnetic, mechanical, pneumatic, radioactive, and thermal; Hirtz et al., 2002), which grows slowly as our understanding of the physical universe deepens. For example, as dark energy and dark matter become better understood, new members may be added to the lists of energy and force. Because these lists grow slowly, we will focus on the faster growing lists of objects and materials. There is often an ambiguity between a material and an object. The wax of a candle is a material, but formed properly, the material becomes an object: a candlestick. Velvet is a material, but any amount of velvet can be considered a piece of velvet (i.e., an object). For this reason, in our arguments we will focus on the number of objects and subsume materials into the set of objects as many materials can easily be made into an object.

5.1. Number of possible objects grows daily

The number of different types of objects grows regularly with no end in sight. Descriptions of new objects are submitted daily to patent offices around the world. Each new object is unique, which means it is associated with a unique set of effects that it can produce in interactions. Our object of interest could interact with any object in this growing list of new types of objects and produce new effects, which translates into a potentially ever-growing number of features for our initial object. We are never sure whether tomorrow a new type of object will be invented that interacts with our object of interest and produces a new effect. The search never ends for new effects as new types of objects emerge each day for our object of interest to interact with.

5.2. Nonenumerable set of interactions

Let us briefly assume that this expansion of new objects continues unimpeded forever, resulting in a countably infinite set of novel types of objects. Given our object of interest, how many subsets of novel objects are there to interact it with, considered over all time and into the future? As the number of subsets of a countably infinite set is uncountably infinite, the number of interactions to examine involving our object of interest is not computably enumerable. No Turing machine could search through this set of interactions even if it was allowed to run for an infinite amount of time.

Is the assumption of a countably infinite set of novel objects plausible? According to Kauffman (2008), there is a penumbra of the adjacent possible that surrounds the space of what is actual. For our purposes, this penumbra represents the objects that are most likely to be invented next. Given this view, as the space of what is actually invented continues to expand, there seems to be no a priori reason why the surrounding space of the adjacent possible would not always exist. Further, there seems to be no a priori reason why nonobvious, novel, and useful (and thus patentable) objects could not continue to be invented without limit.

With the assumption of a countably infinite number of new objects, we easily reach the conclusion of a nonenumerable set of interactions to search through. However, even if we do not make this assumption and fix the number of novel objects at some large but finite number, we can still reach the conclusion (presented in the next section) that the number of possible interactions is so large that for all practical purposes it is still computably nonenumerable.

5.3. Combinatorial explosion of possible interactions

Suppose we have our particular object of interest and there are 10 million other types of objects currently in the world. This is a low estimate given that the US Patent Database alone issued its nine millionth patent on April 7, 2015 (USPTO Database, 2016). Our estimate of 10 million objects makes our calculations easy, although currently it leaves out patents in patent offices from other countries, trade secrets which are in no patent database, as well as the vast set of natural (e.g., stone) and common (e.g., ball) types of objects that are also not contained in any patent database. If we also included unique patents from other countries, trade secrets, as well as natural and common objects, the combinatorial explosion would become even greater. For the purposes of our mathematical arguments, however, it is better to keep our estimate of objects low. It is less controversial to round up to 10 million from the current number in the US Patent Database than make a wilder, higher estimate that includes objects from other patent databases, trade secrets, as well as common and natural objects. Even with a low estimate of objects, however, the number of possible interactions becomes astronomically large, so large as to be computationally unexplorable. Thus, this low estimate is sufficient to make our mathematical point.

Given this working estimate of 10 million types of objects, if we consider our object of interest interacting with each of the 10 million objects separately, then we need to look at 10 million different interactions. However, this assumes that an interaction between just two objects is sufficient for our search. To reveal superconductivity in a ceramic object, for example, we could not just interact the ceramic with something that produces electricity alone or with something that produces an extremely cold temperature alone. We needed to interact the ceramic object with both the electricity-producing object and the object producing extremely cold temperatures at the same time that we are using an object to measure the resistance of the ceramic material to the flow of the electricity. Therefore, we must consider the interaction of more than two objects at a time.

In general, let us consider the size of our space of possible interactions. Suppose our system includes n objects. The number of subsets for the number n is 2 ⁿ . Considering the case of n = 10 million entails 2 ^10,000,000 possible subsets of these 10 million objects that could interact with our chosen object. How big is this number? Given that there are approximately 2 ²⁴⁰ atoms in the universe (which is less than but approximate to the usual estimate given in base 10, which is 10 ⁸⁰ ), 2 ^10,000,000 is a huge number! Therefore, the number of subsets far exceeds the number of atoms in the universe.

Let us consider whether a computer could process the set of subsets if allowed to run for the entire age of the universe. The universe is estimated to be about 14 billion years old. In seconds, this is approximately 4 × 10 ¹⁷ s. Converting to base 2, we get approximately 4 × 10 ¹⁷ = 4 × (5 × 2) ¹⁷ > 4 × (4 × 2) ¹⁷ = 2 × 2 × (2 × 2 × 2) ¹⁷ = 2 ⁵³ s that the universe has existed.

If we had the ability to process each subset in 1 s, then we would need to process 2 ^10,000,000 /2 ⁵³ = 2 ^9,999,947 subsets each second during the entire history of the universe in order to explore all the subsets. Of course, this is impossible, so exploring and processing this entire space of subsets is for all practical purposes uncomputable.

However, we usually do not deal with an extremely large number of objects interacting at one time. Usually, we deal with a modest number. For example, let us consider a human engineer who is considering interactions between the chosen object and between one and five objects at a time (i.e., 5-element sets) from a total set of the 10 million available. Thus, in terms from combinatorics, we will consider the sum of (10 million choose 1) + (10 million choose 2) + (10 million choose 3) + (10 million choose 4) + (10 million choose 5), which is on the order of 10 ²⁷ .

If a computer were processing these subsets from the beginning of the universe (i.e., 4 × 10 ¹⁷ s), then it would have to process approximately 10 ²⁷ /10 ¹⁷ = 10 ¹⁰ subsets per second. As of June 2015, the fastest computer was the Tianhe-2 supercomputer; it processes 3.386 × 10 ¹⁶ floating-point operations per second (Top500 Lists, 2015). Our computations will require slight adjustments as supercomputers grow faster and will require major adjustments on the day that quantum computation takes hold. For now, the Tianhe-2 computer will give us a sense of the magnitude of the feature space of an object. If the Tianhe-2 supercomputer had existed since the beginning of the universe and the processing of each subset required executing just one instruction, then the Tianhe-2 supercomputer would be up to the task of examining the interactions of up to five objects. Of course, the Tianhe-2 supercomputer has not existed since the beginning of the universe, and examining a single subset requires executing more than one instruction. In the next section, we will show that there are so many different ways that objects can possibly interact that the list of possible interactions of two objects might very well be nonenumerable in itself. Thus far, we have assumed that given a set of objects, it is obvious how they should interact.

In a more realistic timeframe, computers have existed from the 1950s until now, which is approximately 2 × 10 ⁹ s. Therefore, if a computer were processing these subsets from the time of the invention of a computer, it would have to process approximately 10 ²⁷ /10 ⁹ = 10 ¹⁸ subsets per second for approximately 70 years. If the Tianhe-2 supercomputer had existed 70 years ago, it would not be quite up to the task of examining 10 ¹⁸ subsets per second for 70 years.

If we wanted to process all 10 ²⁷ subsets in just 1 year, a computer would have to process 10 ²⁷ /10 ⁷ = 10 ²⁰ subsets per second for an entire year (as there are 3 × 10 ⁷ s in a year). Again, the Tianhe-2 supercomputer is not quite up to the task. It would take 10,000 (i.e., 10 ⁴ ) Tianhe-2 supercomputers running in parallel to accomplish this task. Hence, for current computing speeds and for advances in speed in the near future, the task of examining 10 ²⁷ subsets of interacting objects is so large that it is for all practical purposes uncomputable.

Again, we have made two significant simplifying assumptions in our calculations. First, we assumed that a subset of interacting objects could be inspected by executing just one floating-point operation. This is an unreasonable assumption. Second, given just one of these subsets of interacting objects, we assumed that it is easy to determine all the ways that these objects could interact. The number of different ways that one of these subsets of objects could interact might itself be nonenumerable. To get a sense of this possibility, in the next section we will consider all the possible ways that two objects could interact with each other.

5.4. Many ways for objects to interact

Given even two objects, there are many ways that the two could interact. For example, consider two common objects: a ceramic coffee cup and a checker, the small round disk usually made from plastic or wood that is used in the game of checkers. Placing a checker underneath the cup will most likely keep the cup from touching the table, thus serving as a kind of coaster (although moisture will still make it onto the table). If the cup is hot, the checker beneath it will act as a kind of trivet, keeping the heat of the cup from damaging the table. However, there are many other ways that a checker and a coffee cup could interact. A checker could be held in the fingertips and used to stir the liquid inside the cup. In a similar way, a held checker could also be used to scoop off the skin of hot cocoa. A checker could be rattled inside a shaken cup to make a startling noise. A checker could be propped under the lip of an upside down cup to make a trap for a mouse. In essence, there are many ways that a cup and a checker could interact. People with different areas of expertise may very well suggest different ways of interacting the two items. No one person could probably list out every possible way. Working together, many people could add to the list of interactions, but more than likely, the list will always be incomplete. To list out all possible ways of interacting, we would have to consider the aspects mentioned in the next paragraph and, possibly, other aspects that we have overlooked.

For the moment, let us just consider all the ways that the coffee cup and checker might interact by themselves (without bringing in other objects or human hands to manipulate the objects). Can we enumerate all the ways that a checker and a coffee cup might interact by themselves alone? First, we must specify every spatial position that the cup and checker could be in relative to each other. Second, we need to consider every possible type of movement (e.g., linear, nonlinear, or spinning at various angles), speed, and acceleration/deceleration that each object could undergo. Third, we need to include different lighting conditions, heating conditions, radiation conditions, barometric pressures, humidity conditions, and, for some applications, gravity strengths, as well as other types of conditions that we are probably forgetting. If one believes that any one of these variables is a continuous variable and thus needs to be measured by a true real number with unlimited number of digits, then the number of possible ways to interact these two objects in these conditions is truly nonenumerable. Even if all of these variables are measured by real numbers with a finite number of digits, still the number of possible conditions that the objects are interacting within is incredibly large and difficult to approximate.

Are all these digits in precision necessary when counting the number of interactions? Are two interactions really different when they differ in the 100th digit of a variable, for example? In most cases, probably not, but phase transitions are another matter. It is crucially important that, as one nears phase transitions (e.g., liquid water becoming gas as the temperature approaches a critical point or superconductive materials achieving zero electrical resistance when cooled below a critical temperature), small changes in one variable can result in a large discontinuous change in another variable. In the search for new effects, small changes in certain variables may occasionally reveal sudden new phase transitions that produce drastically different effects. Not knowing beforehand that a phase transition is approaching would mean that two interactions that differ by a small degree on a variable could lead to quite distinctive effects.

At the very least, the many possible ways that two objects could interact in a plethora of conditions adds orders of magnitude to the calculations in our previous section. Each of the subsets of objects may interact in an incredibly large number of ways, quite possibly a nonenumerable number of ways.

Thus, our estimates of the 10 ¹⁰ subsets processed per second from the beginning of the universe, the 10 ¹⁸ subsets per second since the invention of the computer, and the 10 ²⁰ subsets per second for a year each need to be increased by at least several orders of magnitude. This increase would make our calculations of the previous section even more uncomputable. At most, the number of possible interactions between two objects may become computably nonenumerable by itself.

5.5. Number of uses of an effect

Besides the question of the enumerability of a set of interactions, another important issue is the number of uses an effect of an interaction might have. An interaction produces effects. An effect of an interaction is useful if the effect satisfies a human goal. We will consider a goal to be a set of desired effects. In our example of the checker leaning against a cup, if the goal is either interact the checker with the cup or lean the checker against the cup, then the goal is trivially satisfied. Therefore, any interaction and any effect can be trivially said to be useful as it fulfills at least one goal and perhaps more.

In a less trivial sense, how many uses does an effect of an interaction have? We will describe several ways to expand interactions so that the effect satisfies a goal. Each of these ways seems to make the effect useful in an unlimited number of ways. Thus, we will suggest that an effect can have an unlimited number of uses.

First, what appears to be a useless effect for one person, say leaning a checker against a cup, for example, may be useful for another person: the checker may mark this cup as belonging to a certain person so as not to confuse this cup with another one. In other words, any effect could be used as a sign of something else. The leaning checker is useful because of the meaning that is projected onto it by some person. Notice that during this projection of meaning, the interaction was expanded from just the checker leaning against the cup to include other people, each of whom might own the cup.

Second, let us expand the interaction to be part of a larger causal chain that is useful. As one example, a checker leaning against a cup could be said to be holding a broken chip of the cup in place while glue dries the chip permanently in place. The leaning checker is now deemed to be useful because it is holding a drying chip in place. As another example, the leaning checker could be steadying the coffee cup from sliding across a tabletop as a cruise ship gently rolls on the waves. The leaning checker is now useful because it prevents the cup from sliding. The leaning checker could be used to block some crucial information from view in the newspaper that the cup and checker are resting upon. By interacting the cup with the leaning checker and just about any other entity (e.g., object or energy), one could most probably devise a use for the leaning checker. For example, as the checker leans against the cup at an angle, a strong light could cast a shadow on our cup–checker pair and project the perfectly shaped triangle onto the table so a math lesson could be taught. A parent might consider his or her child's music to be too loud if the music causes the cup and checker to vibrate so much that the leaning checker falls. There seems to be no inherent limit to the number of causal chains involving other entities that could be constructed, each of which gives the leaning checker a different use.

In these examples, the distinction is emerging between the world of physical causality involving interacting objects and the world of human goals. It seems that every interaction between objects is just a physical interaction that produces physical effects that have no inherent usefulness on their own. To make an interaction useful, we need to take an additional step: set the interaction within the realm of human goals. Perhaps, it will be obvious how the interaction is useful (i.e., which effect of the interaction satisfies a human goal). Perhaps, we will need to explicitly make the interaction useful by employing at least one of two methods: consider the effect of an interaction to be a sign of something else (e.g., the leaning checker is a sign of who owns the cup), or embed the effect in a larger causal chain that is deemed useful (e.g., the leaning checker is holding a drying chip in place). By using these two techniques and perhaps others, we can create a potentially unlimited number of uses for the leaning checker. We can never be sure that our list of uses is complete. Tomorrow, a new object or material could be invented that could trigger the construction of a new causal sequence that leads to a new use for the checker leaning against the cup.

5.6. Automatic derivation of an effect from an interaction

Can a computer automatically derive effects given a set of entities and how they are interacting? It depends on whether a theory exists that can predict those particular effects. For example, general relativity predicted that light would not always travel in straight lines, but would warp when passing by massive objects (Einstein, 1920/2004). This prediction was verified by Arthur Eddington in 1919 during a total solar eclipse. Light from stars nearly behind our sun relative to the Earth passed through the sun's gravitational field and became visible during the eclipse at a position predicted by general relativity (Kennefick, 2009). In contrast, dark matter was postulated as a type of matter that has gravitational effects but does not interact with the entire electromagnetic spectrum (Trimble, 1987). As galactic clusters did not have enough mass to account for their orbital speeds, dark matter was hypothesized to exist as a way to add sufficient gravity to correct for this discrepancy (Zwicky, 1937). The existence of dark matter is far from settled as some scientists are attempting to account for the observable aberrations through more standard theories (Kroupa et al., 2010; Angus, 2013).

In the case of dark matter, empirical observation was ahead of theory, so no theory predicted the existence of dark matter or foresaw the need to alter standard theories to account for the empirical discrepancy. In brief, automatic derivation of a new entity was not possible because empirical observation was required to introduce the need for a new entity. Further, knowing the effect of gravity on the orbiting speeds of galactic clusters was insufficient to fully determine the interaction that produced this effect. If empirical observation is ahead of theory, then the theory is missing members of at least one of the following categories (and maybe multiple categories): entities, interactions, and effects. If all present theories are insufficient, then no algorithm exists that can name and predict the needed entities, interactions, and effects.

5.7. Summary

Given that a feature of an object is an effect of an interaction between the object and other entities (i.e., objects, materials, energies, and forces), there are several conclusions about the sizes of various sets. First, because the number of new objects grows daily, the number of objects to interact with steadily grows, and thus we are never sure that some future interaction with a new object will not yield a new effect (i.e., feature) for our object of interest. Second, if the growth of new objects continues unimpeded through all of time, then the number of objects is countably infinite and the number of potential interactions becomes uncountably infinite (and thus nonenumerable). Third, even if we fix the number of objects at its current number today, still the number of possible interactions is incredibly large and thus practically nonenumerable. Fourth, given just two objects, there is an incredibly large number of ways these two objects could interact: a nonenumerable set of ways if we believe in continuous variables and an incredibly large and unspecified number even if these variables are treated as discrete. Fifth, given a particular effect of an interaction between two objects, the number of uses for this effect is seemingly without an inherent limit. Sixth, empirical fact can, at times, be ahead of a theory's ability to derive certain effects and thus ahead of an algorithm's ability to derive those effects.

The search for obscure (i.e., commonly overlooked and new) features is crucial in the ongoing quest for innovation. The nonenumerability of the set of interactions involving an object means that neither human nor machine can list them out. If no theory is sufficient to predict a certain effect, then no algorithm exists that can derive that effect from currently known entities and interactions. As humans and machines have different search biases, this means that humans are still useful for empirical observation and theory construction, which includes positing entities and crafting interactions to help explain unaccounted for effects. Given this state of things, we opt to devise a collaboration model of innovation between humans and computers in which computers counteract human weaknesses to innovation and humans return the favor. Toward this end, we craft a human- and machine-friendly problem-solving grammar and visualization method. Implemented with the grammar and visualization method will be techniques that counteract known human cognitive obstacles to innovation.

6. HUMAN–MACHINE-FRIENDLY SYNTAX FOR PROBLEM SOLVING

The Nietzschean definition of feature immediately leads to an understanding of the concepts necessary for problem solving and a precise syntax for expressing those concepts. This problem-solving syntax is language-like so it is human friendly and sufficiently structured so that it is easily machine parsable. Basically, problem solving can be described as a search for a sequence of interactions among entities (i.e., objects, materials, energies, and forces) that produces the effects articulated by the goal. In these terms, a goal is a set of desired effects. An interaction is an event in which a group of entities influence each other. Effects are produced when a set of entities mutually influence each other. A feature is synonymous with an effect.

From this interrelated set of concepts, we can construct a grammar to describe the problem-solving process. Using the Extended Backus–Naur Form (EBNF; Aho et al. 1986), which is a compact notation mostly used to define the syntax of computer programming languages, we introduce the EBNF notation as needed. In EBNF, the “::=” symbol means “is defined as.” An item superscripted with a “+” means that there can be one or more occurrences of that item. Because a goal is a nonempty set of desired effects, it can be notated as goal ::= effect⁺ (see Fig. 1).

Fig. 1. Problem-solving syntax.

A person can have a goal if he or she is not currently satisfied with something about the world. In other words, either a change is desired (e.g., reduce concussions in football players) or a change is looming and one wants things to stay the same (e.g., maintain brain health in football players during and after an impact). In the world of engineering, it is well established that any goal can be expressed by an action verb (Hirtz et al., 2002). The verb reduce, for example, expresses the change wanted in a goal, and the verb maintain expresses the desire for no change.

Building on Hirtz et al. (2002), almost any goal can be phrased in the form verb nounPhrase prepositionalPhrases (McCaffrey & Krishnamurty, 2014; McCaffrey et al., 2014). The noun phrase of the articulated goal (e.g., concussions and brain health) describes what needs to be changed (or left unchanged). The prepositional phrases (e.g., in football players and in football players during and after an impact) describe important relationships and constraints.

In EBNF notation, an item superscripted with a “*” means that there can be zero or more occurrences of that item. As an effect might at times be described without any relationships or constraints (e.g., reduce concussions), and thus no prepositional phrases, the official syntax would consist of effect ::= verb nounPhrase prepositionalPhrase* (see Fig. 1).

Because feature and effect are synonymous terms, they use the same syntax. However, a shorthand syntax can be used in certain cases. For example, instead of describing a football helmet's weight as the effect of interacting the football's helmet mass with the Earth's gravity, the adjective heavy might suffice as the feature's description in this context. Further, a helmet's chin strap is a part of the helmet, and thus a feature, so a simple noun phrase chin strap can be used to express it. In the EBNF syntax, a straight line represents logical OR, so feature ::= effect | adjective | nounPhrase (see Fig. 1).

Finally, straight brackets indicate that the item inside the brackets is optional. Words in bold represent key words that appear literally in the strings of the grammar. EBNF also contains other notational symbols that are not required for our problem-solving syntax.

In sum, the above syntax covers the concepts that are needed for problem solving. The syntax is language-like in that expressions are worded in ways that are natural for English speakers to understand. The syntax is sufficiently structured so that the phrases are easily machine parsable. Because the problem solving grammar is both human and computer friendly, it serves as a language through which humans and computers can collaborate while problem solving together. In the next section, we add a visual component that will make human–computer collaboration even easier during problem solving.

7. VISUALIZING PROBLEM SOLVING

A common way to envision problem solving is to conceive of it as a back-and-forth process between top-down problem framing and bottom-up problem solving (Rittel & Webber, 1984; Simon, 1995). Problem framing refines the goal by improving upon its specificity and accuracy. In our view, problem solving includes uncovering little-known features of the available objects followed by interacting them together to accomplish the desired effects expressed by the goal. We will segment the problem solving process into two subprocesses: uncovering little-known features and devising interactions to produce relevant effects. This three-way division (one for problem framing and two for problem solving) is compatible with the function–behavior–structure (FBS) model (Gero, 1990; Gero & Kannengiesser, 2004). In the FBS framework, function (F) tells us what the object is for, behavior (B) tells us what the object does, and structure (S) tells us what the object is.

In the problem-solving process, we generally know what the object will be for, but we do not yet have the object (a kind of abductive reasoning; Dorst, 2011). In other words, we generally know the desired function, but we do not yet know the specifics of its behavior and structure. In problem solving, FBS becomes goal–interactions–entities, with objects being just one type of entity. Function (F) corresponds to the set of effects that we want the object to accomplish (i.e., the goal). Behavior (B) corresponds to the set of interactions that produce those desired effects (i.e., satisfy the goal). Finally, structure (S) corresponds to the set of features of an object, including its parts.

During problem solving, people generally switch between refining the goal, uncovering features of the objects, and devising interactions. Based on Figure 2, goal refinement grows downward while feature unconcealment grows upward. When the proper interactions are devised, the two networks become connected and the problem has its first possible solution.

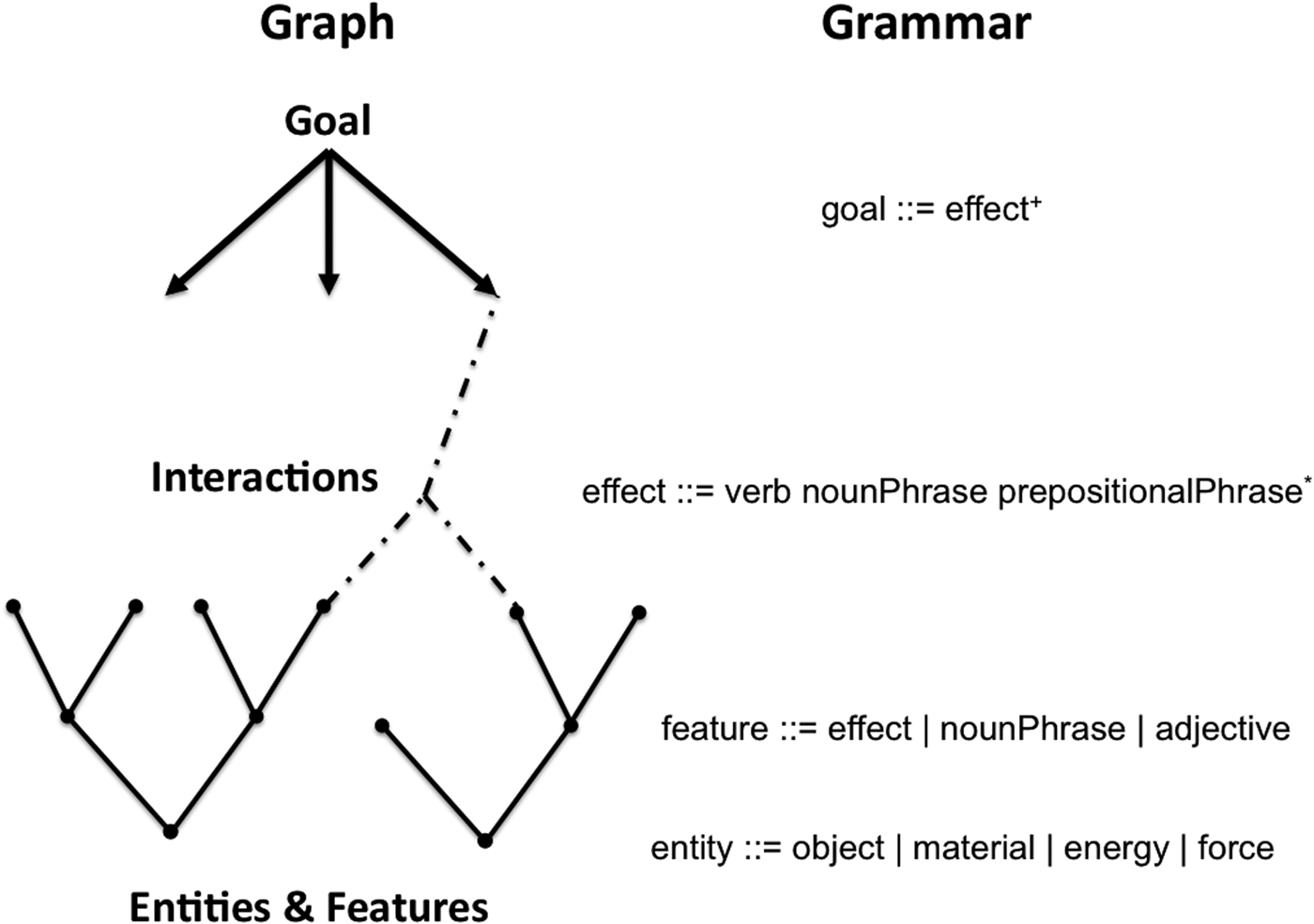
Fig. 2. Three areas of problem solving.

Figure 2 shows the bidirectional graph on the left and the syntax that corresponds to each graph component on the right. The grammar matches up nicely with the graph, except for one minor adjustment. In the graph, the dotted lines convey which entities (including objects) and features are involved in an interaction, so the grammar does not need to list these explicitly. For an interaction on the graph, the grammar only needs to express the relevant effect(s) produced by that interaction.

In the next section, we will work through a concrete problem-solving example in order to illustrate how the graph and the syntax work together.

8. EXAMPLE INVOLVING HUMAN OBSTACLES TO INNOVATION

Humans have certain biases that inhibit innovation, as do machines. Using our problem-solving graph and grammar in Figure 2, we will illustrate how humans and machines might help each other solve an illustrative problem called the two rings problem (McCaffrey, 2012). Humans created machines, so the inhibitive biases possessed by humans might be passed on to the machines they create. Although human and machines biases are probably correlated, humans can create techniques that help counteract their own biases and blind spots. As a mundane example, humans have created spell checkers to overcome our propensity to overlook such things as double occurrences of small words (e.g., “encyclopedia of of knowledge”) and certain commonly inverted letters (e.g., “neice” instead of “niece”). As we will soon show, humans can only list about eight synonyms of a verb, while a computer can easily list out as many synonyms as there are in a thesaurus. Further, software named Analogy Finder (McCaffrey, 2013) can conduct searches to find adaptable solutions to a problem (i.e., analogous solutions) that are outside an individual person's areas of expertise. In contrast, as we have seen in Section 5.6, humans can help machines overcome limits to the features that they can list out about an object. When there is inadequate theory to predict some of the effects of an interaction, then humans are useful for carrying out the interaction, measuring its effects, and recording those effects for the computer.

In the two rings problem, two 6-in. steel rings weighing 3 lb each need to be fastened together in a figure-eight configuration so that when one ring of the configuration is picked up, the other ring will securely come along as well. To accomplish the fastening, all one has to work with is a long candle, a match, and a 2-in. cube of steel. The rings are too heavy for melted wax to securely bond them together, so a solution relies on noticing that the wick is a string that, when extricated from the wax, can tie the rings together.

Initially, we enter the goal at the top of our problem-solving diagram (Fig. 3). The available entities (objects, in this case) are placed at the bottom of the diagram.

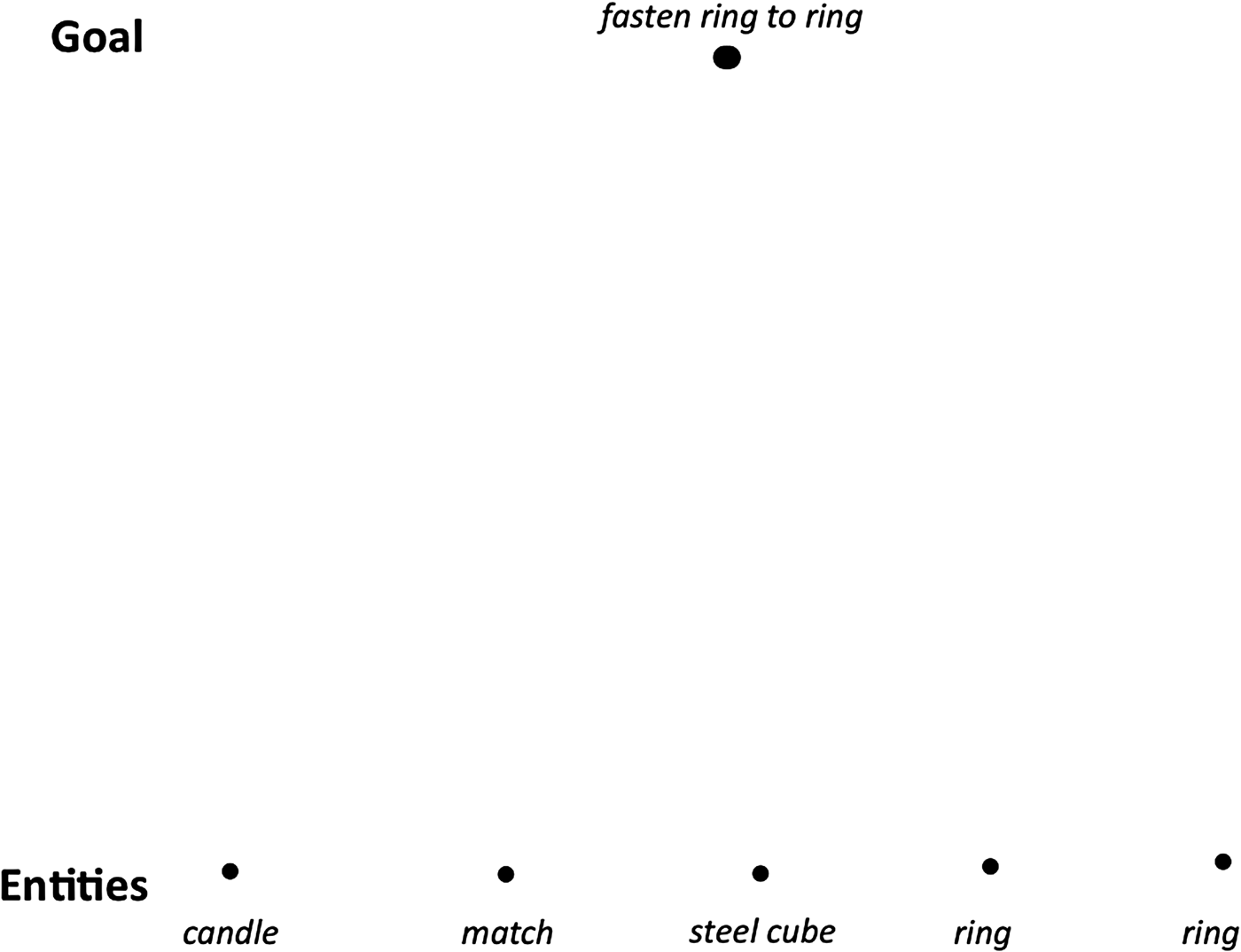
Fig. 3. Initial setup for two rings problem.

Next, for the goal verb fasten, software looks up its more specific synonyms (i.e., hyponyms) from WordNet (Miller, 1995). Each hyponym of a general verb like fasten suggests a specific way to enact the fastening (e.g., weld, staple, clip, tie). Humans tend to be able to list only 8 (plus or minus 2.8) synonyms of verbs (McCaffrey & Spector, 2012), while the verb fasten has 61 hyponyms and 33 hypernyms (i.e., more general synonyms such as attach, adjust, and change). A simple look up of hyponyms in WordNet can help counteract a human obstacle to innovation called narrow verb associations (McCaffrey & Spector, 2012). WordNet is a general dictionary, however, and, for the purposes of technical innovation, may need to be supplemented with other sources such as technical dictionaries. Figure 4 shows a few of the hyponyms of fasten.

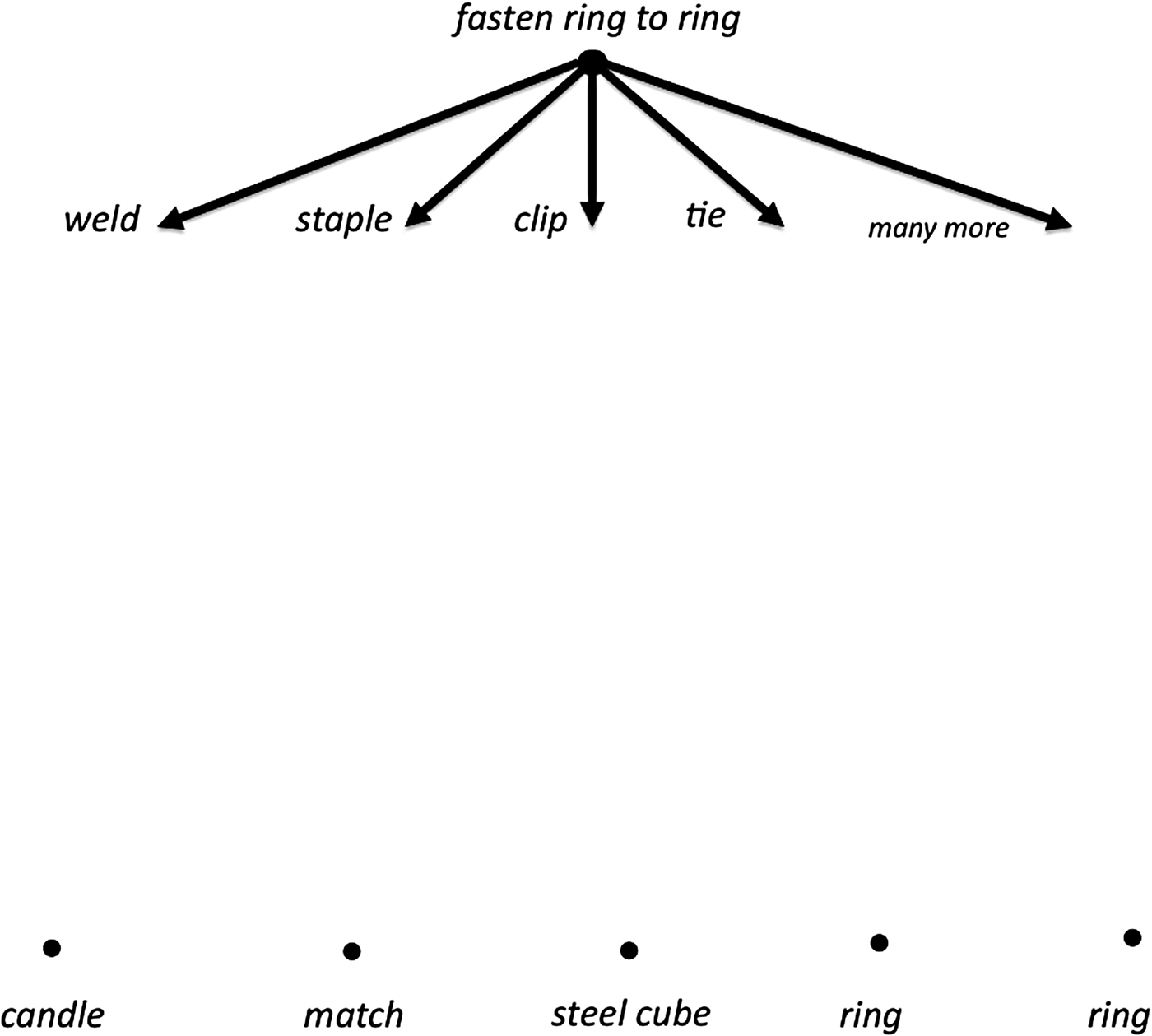
Fig. 4. Goal grows downward with hyponyms.

It is crucial for this problem that the verb tie is a hyponym of fasten. For each hyponym, if a human or machine systematically addressed whether there was any object or part available that could enact that verb (e.g., weld, staple, clip, tie, etc.), this could possibly lead to uncovering the fact that the wick is a string that could tie the rings together.

If the machine representation of candle contained the feature that a wick is a string and the representation of string contained the feature that strings tie things, then the machine can easily make the suggestion that the wick can be used to tie the rings together (McCaffrey & Spector, 2011a, 2011b).

For this example, however, we will assume that the machine is just learning the features of these objects. Once learned, the machine will remember them. However, because an object has a nonenumerable number of features, any object's representation will always be incomplete. Humans can perhaps help fill in some of the features missing from the representation that the machine is currently unable to infer.

Continuing with the two rings problem, we switch from working top-down to working bottom-up. Humans have trouble solving the two rings problem because of functional fixedness (Duncker, 1945), which is the tendency to fixate on the common function of an object or a part. McCaffrey (2012) devised a highly effective technique, the generic parts technique (GPT), to overcome functional fixedness. People using the GPT solved 67% more problems suffering from functional fixedness than a control group.

By analyzing all problems used in the psychology literature that suffer from functional fixedness, McCaffrey (2012) discovered that the solution to all these problems involved uncovering at least one key obscure feature of the objects of the problem, and the types of features that were crucial to solving these problems were the material makeup, shape, and size of the object (or one of its parts). Further, McCaffrey (2012) devised a method to systematically uncover these important feature types. The GPT method involves constructing a parts tree for each object of the problem (see Fig. 5) by asking two questions. First, does your description imply a use? If so, redescribe it in a more generic manner by describing it in terms of its material, shape, and size. Second, can what you are describing be further decomposed into parts? If so, create a new level of the diagram for the next decomposition. Breaking an object into its parts is a step that had been known for some time (Knoblich et al. 1999). However, redescription in a generic manner is the novel contribution of the GPT.

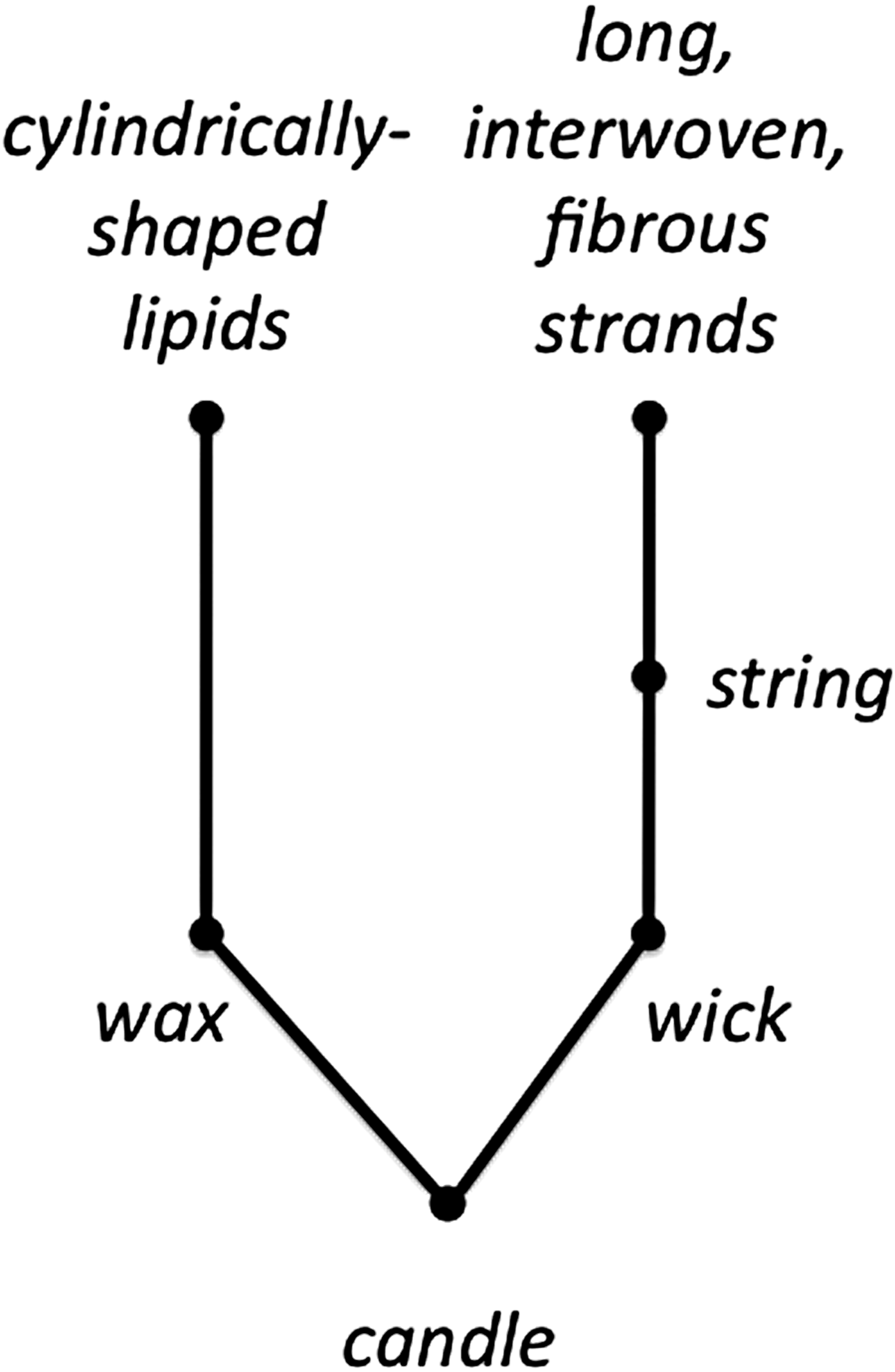
Fig. 5. Generic parts diagram for candle.

For example, in Figure 5, we initially break a candle into its two parts: wax and wick. Working on wick first, the word wick implies a use (i.e., burning to emit light), so we redescribe it, in this case, in terms of its material makeup: string. Up until this point of the graph, people are consistent in how they break down the candle (i.e., wax, wick, and string). From this point onward, however, people's descriptions begin to differ. For example, the word string implies a use: tying things together. Consequently, we again redescribe it in terms involving material, shape, and size. Long, interwoven fibrous strands is one possible description while tangled threads could be another. Because long, interwoven fibrous strands does not imply a use, we are done with this branch of the parts tree. However, tangled threads could imply a use related to sewing, so it should be redescribed more generically.

Because the word wax in this context has a close association with a candle's use, in order to be cautious, we will create a generic description based on one possible shape and material of the wax (e.g., cylindrically shaped lipids is one possible description). People may vary in their description of the material of wax, such as beeswax, which could imply a use for eating or cooking (e.g., use beeswax instead of butter or cooking oil) and thus require a further breakdown into more generic terms. In the light of innovation, these variations in description are not troublesome. Rather, they lead to more ideas for uses of a candle and its parts, especially when the various descriptions by different people are compiled together in one graph. Overall, the GPT systematically strips away the implied uses and reveals more of the “raw object” from which new uses can be devised.

In the two rings problem, we begin to apply the GPT to all of the available objects. For brevity's sake, we start with the candle. The machine guides the human through the GPT by asking questions such as “Does your description imply a use?” and “Can this be decomposed further?” In this example, after the human enters string, he or she almost always has an aha moment on how to solve the problem (McCaffrey, 2011). If not, then the machine intersects the set of all the hyponyms of the goal verb fasten with the set of verbs related to the uses of all the objects and their parts. If the string's representation contains the effect tie things (i.e., in the form verb nounPhrase), then, as shown in Figure 6, the machine is able to make a suggestion that the candle's wick might be able to tie the rings together (McCaffrey & Spector, 2011a, 2011b).

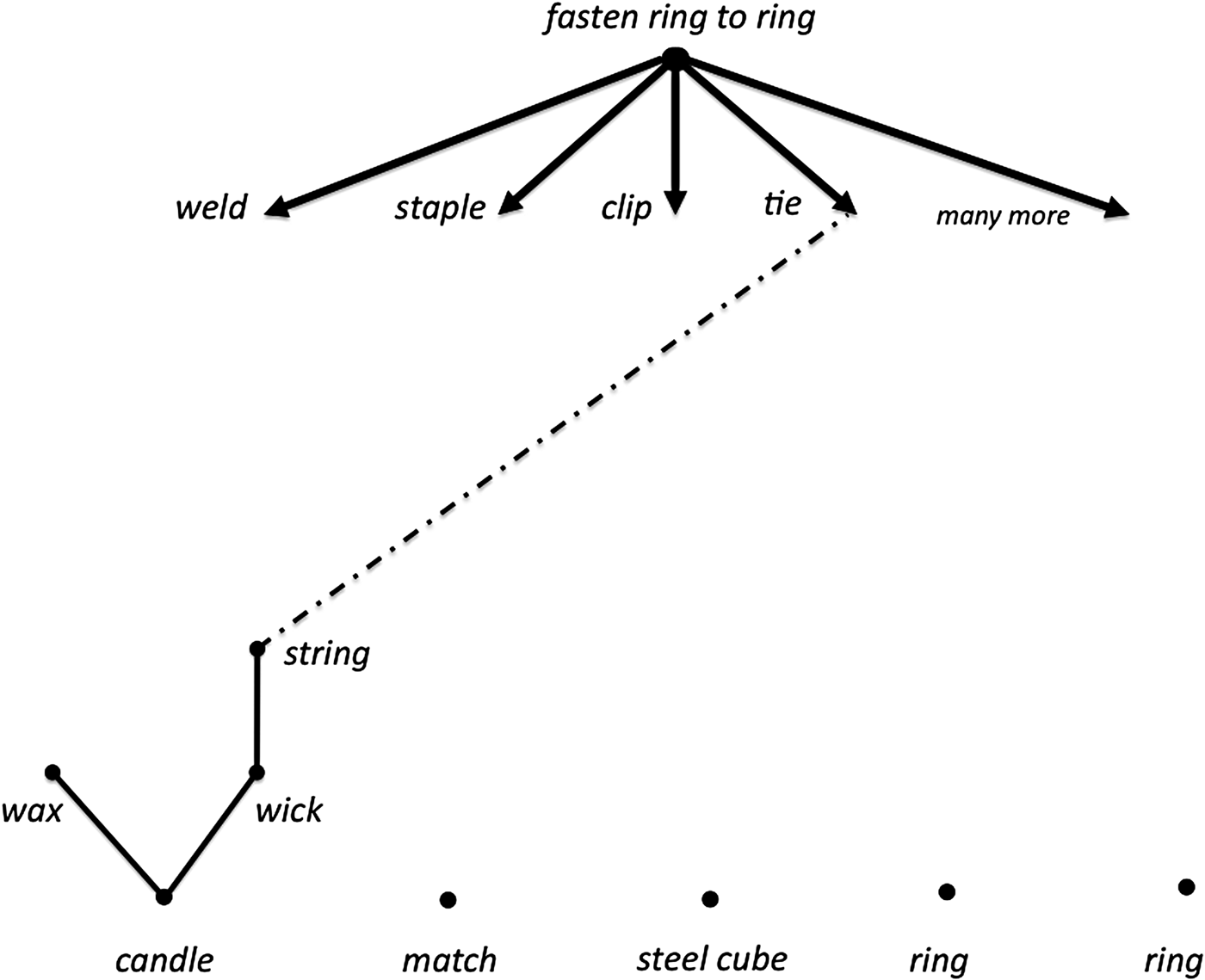
Fig. 6. The key insight for the two rings problem.

Of course, once this conclusion is reached, a new goal becomes necessary: extricate the wick from the wax. None of our human subjects had difficulty figuring out how to scrape the wax away either on the edge of the steel cube or the edge of a table (McCaffrey, 2012). However, if necessary, a new diagram can be started with the new goal: extricate wick from wax.

In sum, the two rings problem shows how the machine can help humans overcome narrow verb associations with hyponym look-ups (McCaffrey & Spector, 2012) and functional fixedness with the GPT (McCaffrey, 2012). In turn, humans can potentially help the machine fill in some of the incompleteness in its representations (McCaffrey & Spector, 2011a, 2011b).

9. A REAL-WORLD EXAMPLE: REDUCE CONCUSSIONS

Whereas the previous section focused on a problem commonly given in psychology experiments, this section will show how to apply and adapt our techniques to a real-world problem: reduce concussions in football players.

Starting with the verb and noun phrase of the goal, reduce concussions, McCaffrey and Pearson (2015) used their software, Analogy Finder (McCaffrey, 2013), to first generate a wide-ranging list of goal phrases. Analogy Finder uses synonyms from WordNet (Miller, 1995) and the verbs for expressing engineering goals from Hirtz et al. (2002) to generate extensive lists: lessen impact, weaken crash, soften jolt, reduce energy, absorb energy, minimize force, exchange forces, substitute energy, oppose energy, repel energy, decrease momentum, and so forth. In the graph of Figure 7, this list grows downward from the initial goal. Relevant entities (i.e., objects and energies, in this case) are listed across the bottom. The various energies come from the 12 types of energy listed in Hirtz et al. (2002). In the context of concussions, different goal phrasings returned different numbers of search results in Google (McCaffrey & Pearson, 2015). At the time, “concussion repel energy” was one of the phrases with the least number of Google search results, which was an indication that repelling energy was an underexplored avenue in the context of concussions. Analogy Finder was then used to search the US Patent database for analogous solutions to the given problem. Specifically, Analogy Finder returns patents that achieve results articulated by the verb–noun pairs. In this way, patents are returned from many different fields, but each returned patent achieves the same or a similar function as that expressed by the original goal (i.e., reduce concussions). Using the results of the Google searches, the Analogy Finder results, and the bidirectional graph of Figure 7, a connection was noticed between the underexplored phrase repel energy and magnets. The idea was then proposed to magnetize all helmets with the same pole so that they repelled each other when in close proximity (Marks, 2015; McCaffrey & Pearson, 2015). In initial testing with models, the helmets both decelerated and slightly altered direction so head-on collisions turned into glancing blows. After approaching the patent office, it was discovered that someone else had submitted the same idea just weeks before we did. Nevertheless, this exercise demonstrated the potential of our process when working on a real-world problem.

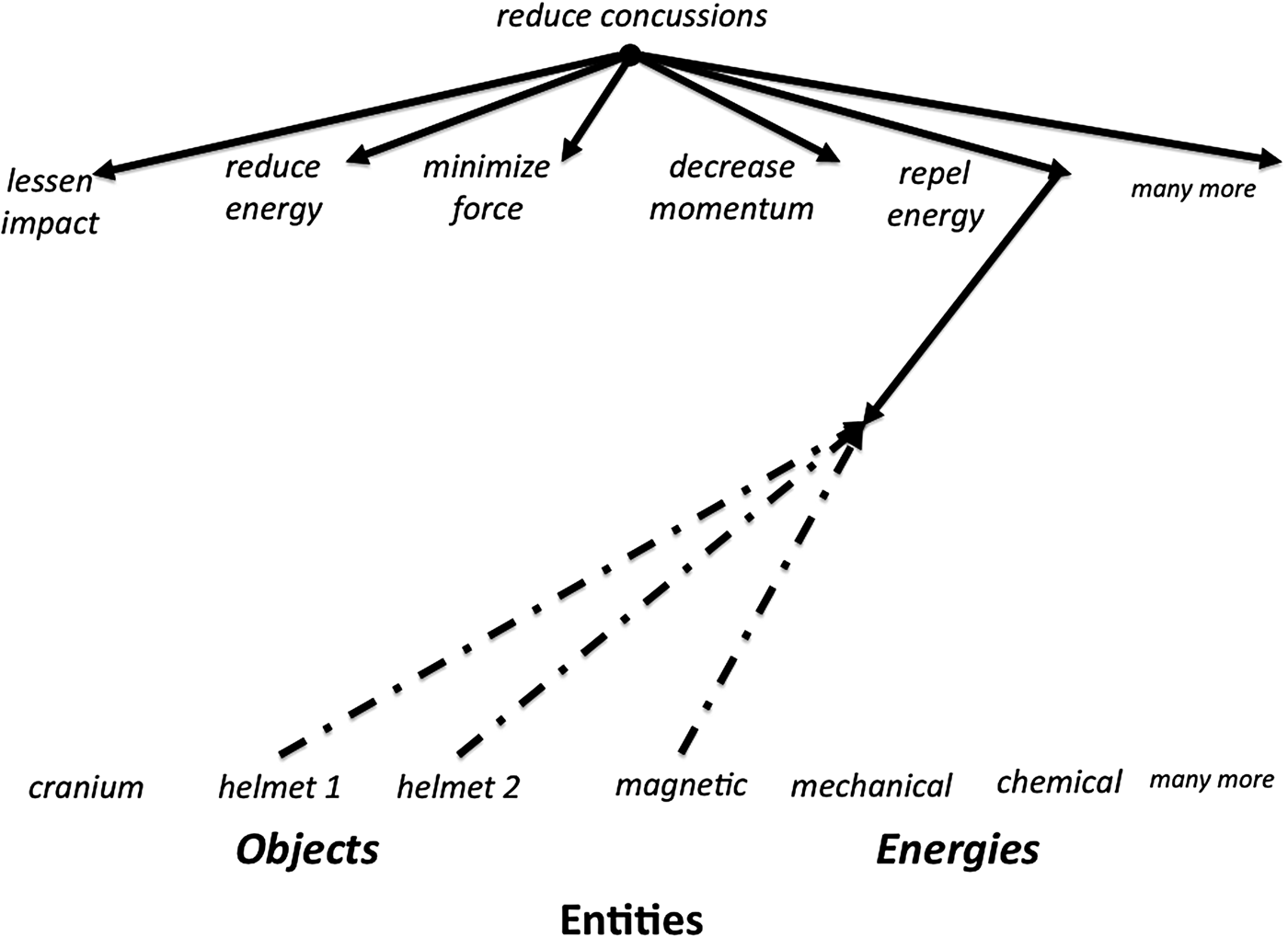
Fig. 7. Problem-solving graph for reduce concussions.

The Analogy Finder software has interesting connections to other design by analogy methods, as well as functional modeling, and these relationships are explored in McCaffrey and Krishnamurty (2014) and McCaffrey et al. (2014).

In sum, systematically rephrasing the goal led to many diverse avenues to explore, each with slightly different nuances. Google searches suggested which avenues had already been heavily explored and which underexplored. Analogy Finder found many relevant patents from other fields that could possibly be adapted to solve the original problem. The systematic listing of many possible energy types ensured that no type of energy was completely ignored. Together, these processes greatly broadened the search for relevant ideas that could address this tough problem.

10. CONCLUSIONS AND FUTURE WORK

The OFH gives a clear focal point for innovative problem solving: namely, an innovative solution relies on uncovering one or more obscure features of the problem. The set of features of an object is equivalent to the set of the effects of interactions that the object can be involved in. The origin of a feature is an interaction, so new features come from new interactions. To search for new features, interact the object with entities (i.e., objects, materials, energies, and forces) that it has never interacted with before.

Depending on assumptions made, the set of interactions is either not computably enumerable (assuming a countably infinite number of new objects) or practically nonenumerable (assuming a large but finite number of objects). Consequently, the search for new features that may emerge from interactions is either truly uncomputable or practically uncomputable. Thus, neither human nor machine can list out all the features of an object. Any representation of an object is incomplete.

Further, empirical results may be ahead of any current theory's ability to account for them. In this case, no algorithm will be able to derive these effects, as well as all the possible interactions and entities involved in producing these effects. Thus, unaccounted for empirical results are another way to reveal the incompleteness of a description.

Given the above uncomputability and the various human weaknesses to innovating (e.g., narrow verb associations, functional fixedness, and analogy blindness, which is counteracted by Analogy Finder), we opt for humans and computers to collaborate when innovating. Computers can help overcome human weaknesses, and humans can return the favor. To this end, we crafted a problem-solving grammar and visualization method that is designed to be easy for both humans and computers to use. In this way, both humans and computers can contribute to the same representation of the problem and assist each other in countering each other's problem-solving weaknesses.

Research has named other human cognitive obstacles to innovation not named in this paper that machines can help with. For example, design fixation (Jansson & Smith, 1991) states that when asked to create innovative designs, humans tend to fixate on the features of designs shown to them even though this limits their creativity. McCaffrey and Spector (2012) devised an effective countertechnique that helps humans shift their focus to types of features they are currently ignoring. A countertechnique has also been developed to help humans overcome assumption blindness (McCaffrey & Krishnamurty, 2014).

Our arguments about the sizes of various sets and their uncomputability give some theoretical sense to the boundaries faced by computation during innovation. However, the innovation system that we are developing, which focuses on how humans and machines can search together for obscure features, should most likely suffice for many practical problems. We will empirically test this statement after the innovation system is fully implemented. All the techniques mentioned in this paper are in the process of being implemented in a software system with funding from National Science Foundation Grant 1534740. Once the software is implemented, experiments are planned to test its influence on ideation, problem solving, innovation, and creativity. Future research will also compare our completed innovation system with other methods used in knowledge engineering and machine intelligence.

As innovation research continues both on the human and machine sides, further obstacles to innovation will most certainly be uncovered. Hopefully, techniques for counteracting those obstacles will also be discovered. The eventual result will most likely be a partnership, a human–machine synergy, which is more innovative than either partner working alone.