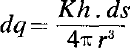The general technique for rendering approximate solutions to physical problems uniformly valid is here applied to the simplest form of the problem of correcting the theory of thin wings near a rounded leading edge. The flow investigated is two-dimensional, irrotational and incompressible, and therefore the results do not materially add to our already extensive knowledge of this subject, but the method, which is here satisfactorily checked against this knowledge, shows promise of extension to three-dimensional, and compressible, flow problems.
The conclusion, in the problem studied here, is that the velocity field obtained by a straightforward expansion in powers of the disturbances, up to and including either the first or the second power, with coefficients functions of co-ordinates such that the leading edge is at the origin and the aerofoil chord is one of the axes, may be rendered a valid first approximation near the leading edge, as well as a valid first or second approximation away from it, if the whole field is shifted downstream parallel to the chord for a distance of half the leading edge radius of curvature ρL. It follows that the fluid speed on the aerofoil surface, as given on such a straightforward second approximation as a function of distance x along the chord, similarly is rendered uniformly valid (see equation (52)) if the part singular like x-1 is subtracted and the remainder is multiplied by 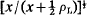 .
.

 .
. if the boundary layer is completely turbulent. The drag coefficient of the N.A.C.A. 64-012 section, however, varies closely as cos
if the boundary layer is completely turbulent. The drag coefficient of the N.A.C.A. 64-012 section, however, varies closely as cos