Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T11:02:43.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Wall Jets on Logarithmic Spiral Surfaces

Published online by Cambridge University Press:  07 June 2016

J. A. Giles ,
A. P. Hays  and
R. A. Sawyer
J. A. Giles
Affiliation:
Aeronautical Engineering Department, Bristol University
A. P. Hays
Affiliation:
Aeronautical Engineering Department, Bristol University
R. A. Sawyer
Affiliation:
Aeronautical Engineering Department, Bristol University
Get access

Summary

By considering the equations of motion it has been shown that the flow in the outer part of a two-dimensional, curved, turbulent wall jet is approximately self-preserving if the ratio of jet thickness to wall radius of curvature is constant along the jet. This condition is satisfied for a jet blowing over a surface of logarithmic spiral profile, for which the radius of curvature R increases linearly with distance s along the wall.

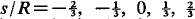Measurements of velocity profiles and rates of growth of wall jets for surfaces with curvature ratios and 1 are presented. These are compared with solutions obtained using an eddy viscosity theory, and with the flow of jets round circular cylinders. The measured jets are found to be approximately self-preserving in form, and to have rates of growth which are much larger than the jets on circular cylinders with corresponding values of s/R.

Type
Research Article
Information
Aeronautical Quarterly , Volume 17 , Issue 3 , August 1966 , pp. 201 - 215
Copyright
Copyright © Royal Aeronautical Society. 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Newman, B. G. The deflection of plane jets by adjacent boundaries—Coanda effect Boundary-layer control—Principles and applications, p. 232. (Edited by Lachmann, G. V..) Pergamon Press, 1961.Google Scholar
2. Fekete, G. I. Coanda flow of a two-dimensional wall jet on the outside of a circular cylinder. McGill University Mechanical Engineering Department Report 63-11, 1963.Google Scholar
3. Glauert, M. B. The wall jet. Journal of Fluid Mechanics, Vol. 1, p. 625, 1956.Google Scholar
4. Bakke, P. An experimental investigation of a wall jet. Journal of Fluid Mechanics, Vol. 2, p. 467, 1957.Google Scholar
5. Bradshaw, P. and Gee, M. T. Turbulent wall jets with and without an external stream. ARC R & M 3252, 1960.Google Scholar
6. Schwarz, W. H. and Cosart, W. P. The two-dimensional turbulent wall jet. Journal of Fluid Mechanics, Vol. 10, p. 481, 1961.CrossRefGoogle Scholar
7. Guitton, D. E. Two-dimensional turbulent wall jets over curved surfaces. McGill University Mechanical Engineering Department Report 64-7, 1964.Google Scholar
8. Sawyer, R. A. Two-dimensional turbulent jets with adjacent boundaries. PhD Thesis, Cambridge University, 1962.Google Scholar
9. Giles, J. A. and Hays, A. P. The flow of two-dimensional turbulent air jets over logarithmic spiral surfaces. Bristol University Aeronautical Engineering Department Report 89, 1965.Google Scholar
10. Young, A. D. and Maas, J. N. The behaviour of a pitot tube in a transverse total-pressure gradient. ARC R & M 1770, 1937.Google Scholar
11. Bradbury, L. J. S. A simple circuit for the measurement of the intermittency factor in a turbulent flow. Aeronautical Quarterly, Vol. XV, p. 281, August 1964.Google Scholar
12. Patel, R. P. Self-preserving two-dimensional turbulent jets and wall jets in a moving stream. McGill University MEng Thesis, 1962.Google Scholar
13. Görtler, H. Berechnung von Aufgaben der Freien Turbulenz auf Grund eines neuen Naherungsansatzes. Zeitschrift für angewandte Mathematik und Mechanik (ZAMM), Vol. 22, p. 244, 1942.Google Scholar