Published online by Cambridge University Press: 07 June 2016
Experimental measurement of the pitching stability derivatives 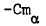 and
and  of AGARD hyperballistic standard models HB1 and HB2, a hemisphere-cylinder double flared configuration designated HBS and three 10° semi angle cones of bluntness ratios 0.0, 0.2 and 0.4 are reported. Data were obtained at a Mach number of 6.85 in a short duration light piston tunnel using the small amplitude free oscillation technique. The tests were conducted at Reynolds numbers from 0.2 × 106 to 0.85 × 106, based on centre-body diameter, for the hyperballistic shapes and from 1.45 × 1016 to 2.17 × 106, based on base diameter, for the conical shapes. The mean angle of attack was varied from 0 to 17.0 degrees and the frequency parameter from 0.0020 to 0.0043 for the hyperballistic shapes and from 0.0018 to 0.0092 for the cones. All models tested were found to be dynamically stable for all positions of the axis of oscillation considered. The significant observed non linear variations of the damping derivative with angle of attack for the 0.2 and 0.4 bluntness cones and the HB2 shape could be partially accounted for qualitatively by boundary layer transition induced effects. The variation of the derivatives with angle of attack for the pointed cone were consistent with a fully turbulent boundary layer, whereas it was probable that for the HB1 and HBS models the boundary layer remained laminar throughout. Variation of the frequency parameter resulted in no significant effect on the measured stability derivatives.
of AGARD hyperballistic standard models HB1 and HB2, a hemisphere-cylinder double flared configuration designated HBS and three 10° semi angle cones of bluntness ratios 0.0, 0.2 and 0.4 are reported. Data were obtained at a Mach number of 6.85 in a short duration light piston tunnel using the small amplitude free oscillation technique. The tests were conducted at Reynolds numbers from 0.2 × 106 to 0.85 × 106, based on centre-body diameter, for the hyperballistic shapes and from 1.45 × 1016 to 2.17 × 106, based on base diameter, for the conical shapes. The mean angle of attack was varied from 0 to 17.0 degrees and the frequency parameter from 0.0020 to 0.0043 for the hyperballistic shapes and from 0.0018 to 0.0092 for the cones. All models tested were found to be dynamically stable for all positions of the axis of oscillation considered. The significant observed non linear variations of the damping derivative with angle of attack for the 0.2 and 0.4 bluntness cones and the HB2 shape could be partially accounted for qualitatively by boundary layer transition induced effects. The variation of the derivatives with angle of attack for the pointed cone were consistent with a fully turbulent boundary layer, whereas it was probable that for the HB1 and HBS models the boundary layer remained laminar throughout. Variation of the frequency parameter resulted in no significant effect on the measured stability derivatives.