Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T10:29:37.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Forced Convection Near Laminar Separation

Published online by Cambridge University Press:  07 June 2016

E.A. Akinrelere
E.A. Akinrelere*
Affiliation:
Department of Mathematics, University of Ife, Ile-Ife, Nigeria
Get access

Summary

The singular behaviour of an incompressible boundary layer at separation has been well established by the works of Howarth (1938), Goldstein (1948), Stewartson (1958), Curie (1958) and Terrill (1960). Stewartson (1962) remarked that the existence of the singularity at separation can be regarded as fully established and understood. The skin friction vanishes like 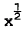where x is the distance to separation, and the stream function close to the wall is described by a series of powers of 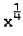, with coefficients that are functions of 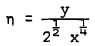, where y measures distance normal to the wall. At some stages in the expansion of the stream function, terms in log x have to be included. The case of the compressible flow is less satisfactory. Stewartson (1962) was unable to establish singularity at separation and concluded that the general compressible boundary layer cannot have a singularity at separation unless there is no heat transfer from the wall. This has been contradicted by the works of Merkin (1968) and Buckmaster (1970). Curie (1958) also reported that the difficulty encountered in computing the temperature field right down to the point of separation might be due to the singularity there. In this paper, the Goldstein-Stewart son approach is applied to laminar boundary layer flow at low speeds in which density is sensibly constant and the Prandtl number σ is taken as unity. Singularity is established at separation for the temperature field. The heat transfer does not vanish at separation point and is of the form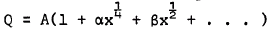

Type
Research Article
Information
Aeronautical Quarterly , Volume 32 , Issue 3 , August 1981 , pp. 212 - 227
Copyright
Copyright © Royal Aeronautical Society. 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Howarth, L. On laminar boundary layer flow. Proc. Roy. Soc. A. p 547, 1938.Google Scholar
2 Hartree, D.R. A solution of the laminar boundary layer equation for retarded flow. Rep. Memor. Aero Res. Coun. No. 2426, 1939.Google Scholar
3 Goldstein, S. On laminar boundary layer flow near a point of separation. Quart. J. Meeh. App. Maths, 1, p 43, 1948.CrossRefGoogle Scholar
4 Jones, C.W. On a solution of the laminar boundary layer equation near a point of separation. Quart. J. Meoh. App. Maths, 1, p 385, 1948.CrossRefGoogle Scholar
5 Leigh, D.C.F. The laminar boundary layer equation: a method of solution by means of an automatic computer. Proc. Camb. Phil. Soc. 51, p 320, 1955.CrossRefGoogle Scholar
6 Stewartson, K. On Goldstein’s theory of laminar boundary layer separation. Quart. J. Meoh. App. Maths. II, p 399, 1958.CrossRefGoogle Scholar
7 Terrill, R.M. Laminar boundary layer flow near separation with or without suction. Phil. Trans. A. 253, p 55, 1960.Google Scholar
8 Curie, S.N. The steady compressible laminar boundary layer with arbitrary pressure gradient and uniform wall temperature. Proc. Roy. Soc. A. 249, p 206, 1958.Google Scholar
9 Stewartson, K. Boundary layer flow near a point of zero skin friction. J. Fluid Meoh. 12, p 117, 1960.CrossRefGoogle Scholar
10 Buckmaster, J. The behaviour of a laminar compressible boundary layer on a cold wall near a point of separation. J. Fluid Meoh. 44, p 237, 1970.CrossRefGoogle Scholar
11 Slater, L.J. Confluent hypergeometric functions - Camb. Univ. Press, 1960.Google Scholar