Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:38:40.261Z Has data issue: false hasContentIssue false
  • English
  • Français

The Decay of a Turbulent Trailing Vortex

Published online by Cambridge University Press:  07 June 2016

P. R. Owen
P. R. Owen*
Affiliation:
Department of Aeronautics, Imperial College, London
Get access

Summary

The decay of a trailing vortex containing a turbulent core is examined according to the argument that the turbulence is partly sustained by, and interacts with, the irrotational flow through viscous diffusion of eddies across the core boundary. The region separating the core from the outer irrotational flow, in which the interaction between the turbulence and the mean flow occurs, expands with time like (time)1/2, characteristic of viscous diffusion.

On the basis of a simple representation of the radial distribution of mean circumferential velocity, the decay of the vortex is calculated and is found to behave in a way similar to what Squire predicted, on the assumption of a constant eddy viscosity, in 1954. The essential difference from Squire’s solution found here is that the apparent viscosity is not simply proportional to the initial circulation about the vortex as he proposed, but depends on the Reynolds number defined with respect to the circulation.

Wind tunnel and flight observations of vortex decay can be more closely reconciled than Squire’s theory allowed; those differences that exist are attributed to the vastly different ages of the vortices in the laboratory and flight experiments. The principal conclusion of practical interest is that the maximum circumferential velocity in a trailing vortex generated by an aeroplane in flight is

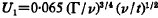
where Γ is the circulation about large circuits enclosing the vortex, v the kinematic viscosity of the air and t the (sufficiently great) age of the vortex.

Type
Research Article
Information
Aeronautical Quarterly , Volume 21 , Issue 1 , February 1970 , pp. 69 - 78
Copyright
Copyright © Royal Aeronautical Society. 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Squire, H. B. The growth of a vortex in turbulent flow. ARC 16,666, 1954. Also Aeronautical Quarterly, Vol. XVI, p. 302, August 1965.Google Scholar
2. Mabey, D. G. The formation and decay of vortices. DIC Thesis. Imperial College, London, 1953.Google Scholar
3. Rose, R. and Dee, F. W. Aircraft vortex wakes and their effects on aircraft. RAE Technical Note Aero 2934, 1963.Google Scholar
4. Newman, B. G. Flow in a viscous trailing vortex. Aeronautical Quarterly, Vol. X, p. 149, May 1959.Google Scholar
5. Dosanjh, D. S., Gasparek, E. P. and Eskinazi, S. Decay of a viscous trailing vortex. Aeronautical Quarterly, Vol. XIII, p. 167, May 1962.Google Scholar
6. Lilley, G. M. A note on the decay of aircraft trailing vortices. College of Aeronautics, Cranfield, Memo 22, 1964.Google Scholar
7. Townsend, A. A. The structure of turbulent shear flow. Cambridge University Press, 1956.Google Scholar
8. Templin, R. J. Flow characteristics in a plane behind the trailing edge of a low aspect ratio wing as measured by a special pressure probe. NAE, Canada, LM AE-58. (Quoted by Newman, 4), 1954.Google Scholar
9. Titchener, I. M. and Taylor-Russell, A. J. Experiments on the growth of vortices in turbulent flow. ARC Current Paper 316, 1957.Google Scholar
10. Hoffman, E. R. and Joubert, P. N. Turbulent line vortices. Journal of Fluid Mechanics, Vol. 16, Pt. 3, p. 395, 1963.Google Scholar