NOMENCLATURE
- A, B
non-dimensional effective begin and end of rotor blade, referenced to R
- c
blade chord, m
- C d0
drag coefficient
- C lα
lift curve slope
- CT
thrust coefficient of the rotorcraft,
 $$
C_T = T/\left( {\rho \pi R^2 U^2 } \right)
$$
$$
C_T = T/\left( {\rho \pi R^2 U^2 } \right)
$$- Iβ
mass moment of inertia about the blade flapping hinge, kgm2
 $$L,\;\overline L$$
$$L,\;\overline L$$blade lift, N; non-dimensional blade lift,
 $$\overline L = L/\left( {\rho U^2 cRC_{l\alpha } } \right)$$
$$\overline L = L/\left( {\rho U^2 cRC_{l\alpha } } \right)$$ $$ M_\beta ,\;\overline {M_\beta } $$
$$ M_\beta ,\;\overline {M_\beta } $$aerodynamic flapping moment about the flapping hinge, Nm; non-dimensional flapping moment,
 $$ \overline {M_\beta } = M_\beta /\left( {\rho U^2 cR^2 C_{l\alpha } } \right) $$
$$ \overline {M_\beta } = M_\beta /\left( {\rho U^2 cR^2 C_{l\alpha } } \right) $$- Nb
number of rotor blades
 $$Q,\;\overline Q $$
$$Q,\;\overline Q $$blade torque, Nm; non-dimensional blade torque,
 $$ \overline Q = Q/\left( {\rho U^2 cR^2 C_{l\alpha } } \right) $$
$$ \overline Q = Q/\left( {\rho U^2 cR^2 C_{l\alpha } } \right) $$- r
non-dimensional blade radial coordinate, referenced to R
- Rc, rc
dimensional and non-dimensional vortex core radius, m and referenced to R
- R, RWT
rotorcraft and wind turbine rotor radius, m
- RCR
rotor control ratio,
 $$ RCR = \Delta \Theta /\Theta _{max} $$
$$ RCR = \Delta \Theta /\Theta _{max} $$- RFR
rotor flapping ratio,
 $$ RFR = \Delta \beta /\beta _{max} $$
$$ RFR = \Delta \beta /\beta _{max} $$- t
time, s
- T
rotor thrust, N
- U
rotor blade tip speed, m/s, U = ΩR
- vV
vortex-induced velocity, m/s
- VT, VP
non-dimensional velocities acting tangential and normal at the blade element, referenced to U
- VW
wind speed, m/s
- V ∞
rotorcraft flight speed, m/s
- x, y, z
non-dimensional hub-fixed coordinates of the rotorcraft, x pos. downstream, y pos. starboard, z pos. up, referenced to R
- x 0, y 0
vortex position within the rotor disk; non-dimensional, referenced to R
- Y
rotor blade radial coordinate, m
- αS
rotor shaft angle of attack, deg
- β, β0, βC, βS
rotor blade flapping angle, mean, and cyclic components, deg
- βmax
maximum available flapping margin, deg
- βtrim
flapping angle present in trim, deg
- βP
precone angle, deg
- γ
Lock number,
- Γ, Γeq
vortex and equivalent straight line vortex circulation strength, m2/s
- δ 3
pitch-flap coupling, deg
- Δ
perturbation of a variable
 $$ \Theta ,\Theta _0 ,\Theta _C ,\Theta _S $$
$$ \Theta ,\Theta _0 ,\Theta _C ,\Theta _S $$rotor blade pitch angle, collective, lateral and longitudinal control angle, deg
- Θtrim
rotor blade pitch angle used for trim, deg
- Θtw
blade pre-twist angle, deg/R
- Θmax
maximum available control margin, deg
- λi
thrust-induced inflow velocity normal to the rotor disk, referenced to U
- λV, λ V0
wake vortex induced inflow ratio and its amplitude, referenced to U
- μ
rotor advance ratio,
 $$ \mu = V_\infty \cos \alpha _S /U $$
$$ \mu = V_\infty \cos \alpha _S /U $$- μz
rotor inflow ratio,
 $$ \mu _z = - \mu \tan \alpha _S $$
$$ \mu _z = - \mu \tan \alpha _S $$ $$ \nu _\beta ,\nu _{\beta eff} $$
$$ \nu _\beta ,\nu _{\beta eff} $$natural frequency of rotor blade flapping and effective natural frequency of flapping, referenced to Ω
- ρ
air density, kg/m3
- σ
rotor solidity,
 $$ \sigma = N_b c/\left( {\pi R} \right) $$
$$ \sigma = N_b c/\left( {\pi R} \right) $$- ψ
rotor blade azimuth, deg
- Ω, ΩWT
rotorcraft and wind turbine rotational speed, rad/s
- AG
autogyro
- BoMR
Bo105 main rotor
- BoTR
Bo105 tail rotor
- COAX
coaxial rotor
- WT
wind turbine
1.0 INTRODUCTION
Vortex-rotor interactions and their impact on the flight mechanics of helicopters were first studied in the 1980s when heliports were planned to be built in the vicinity of airport runways. The subject of interest was the flight of a UH-1 type helicopter into the blade tip vortex from wide-body aircraft, such as the Boeing 747. Experimental(Reference Dunham, Holbrook, Mantay, Campbell and Van Gunst1) and numerical studies(Reference Mantay, Holbrook, Campbell and Tamaine2–Reference Azuma, Saito and Kawachi4) were carried out, concluding that the vortex effect was recognised but no hazardous reaction occurred. The subject again gained interest after 2000 by flight dynamics simulations using a Lynx helicopter model. Potential hazards were found that depended on the vortex position inside the helicopter rotor(Reference Turner, Padfield and Harris5–Reference Lawrence and Padfield7). So far the vortex and the helicopter wake remained unaffected from each other. This topic of mutual interaction and deformation of the vortex as well as of the rotorcraft’s wake were investigated in parallel by computational fluids methods, concluding that the vortex and wake deformation can significantly reduce the vortex impact on the rotorcrafts air loads(Reference Whitehouse and Brown8,Reference Whitehouse and Brown9) . They used the vorticity transport method for both the vortex and the helicopter rotor wake at different encounter speeds. Largest mutual interactions and wake/vortex deformations were found at low speed encounters, due to large thrust-induced velocities in this operational condition. In high-speed forward flight the assumption of a “rigid” vortex is found to be appropriate because the thrust-induced velocities are then much smaller. A Navier-Stokes equations solver was applied recently for both the wind turbine (WT) wake and the rotorcraft wake for simulations of a EC135 helicopter flying straight into the wake of a 5 MW WT. The purpose was to look for variations of rotor thrust during the penetration of the wake spiral(Reference Bühler, Weihing, Klein, Lutz and Krämer10). The flight path was prescribed. In this configuration about 8% thrust variation was computed for a flight at half height of the WT wake where vortices are normal to the helicopter rotor and about 3% when crossing the wake close to the top. However, the flight path was chosen to pass between vortices such that the rotor did not experience the vortex cores. Helicopter encounters of the wake generated by different categories of fixed-wing and also helicopters of different weight class were studied recently with respect to aircraft safety(Reference Jimenez-Garcia, Barakos, Treve, Rooseleer, Cappellazzo and Graham11). They found that the suggested separation distances for aircraft are also appropriate for helicopters.
In the context of large WT, their wake vortex and wind deficit impact on small helicopters found increasing interest in Europe. A GARTEUR action group focused on helicopter operations in WT wakes, focusing on WT wake modelling, small-scale wind tunnel testing of wind farms, isolated vortex-rotor simulations and flight mechanical simulations in a rigid wake tube(Reference Bakker, Visingardi, Van Der Wall, Voutsinas, Basset, Campagnolo, Pavel, Barakos and White12). Simulations with a Bo105 helicopter indicated potential hazardous situations at low speed in immediate vicinity downstream of the WT. Individual members of the GARTEUR group published results on a Bo105 helicopter simulation entering a time-averaged WT wake 2 diameters downstream of the turbine(Reference Andronikos, Papadakis and Riziotis13). Due to the time averaging, the vortex-induced peak velocities are missing, and the wind deficit and the swirl therein is the main contribution of the wake. Required control angles in collective and cyclic are found around 0.3 deg and thus not hazardous. Another study simulated the NREL 5 MW WT wake by free-wake method, again with a Bo105 helicopter entering it 2 diameters downstream(Reference Visingardi and Pavel14). Flights at mid-height of the wake tube, and at half a radius below and up of the mid were computed with the vortex orientation normal to the disk and inclined by about 45 deg, respectively. Again, a time-averaged wake velocity field was computed first, then the helicopter flight into it performed from both sides of the wake. Without pilot action the flapping angles reach 3 deg in total during the passage, associated with a thrust increase peaking at 20% of the nominal thrust. An adverse effect on handling qualities was found.
The rotor controls required to mitigate the WT vortex impact on rotor trim, and the rotor blade flapping that will develop without pilot reaction were recently elaborated analytically(Reference Van Der Wall and Van Der Wall15,Reference Van Der Wall16) . The previous studies concerned a vortex whose orientation is essentially longitudinal or lateral with respect to the rotor disk, representing the rotorcraft flight into the vortex from the side or in longitudinal direction. With respect to WT wake vortices, this represents a flight at the top or bottom of the wake system, either from the side or along its downstream extension, Fig. 1.

Figure 1. Rotorcraft encountering a wind turbine wake, one at the top and the other through the center.
At the upper or lower position, approaching the wake from the side, both the main and the tail rotor experience the vortex longitudinally oriented in their disk, Fig. 2(a). A flight at top or bottom of the spiral in wind direction or against it will have the vortex lateral within the main rotor disk, but perpendicular (orthogonal) to the tail rotor disk, Fig. 2(b). Also, a flight into the wake system through the center of the wake spiral will result in a vortex orientation perpendicular to the rotorcraft main rotor disk, and lateral in its tail rotor, Fig. 2(c). The orthogonal interaction was experimentally investigated using a propeller that was subjected to a wing tip vortex in the wind tunnel(Reference Yang, Zhou, Sciacchitano, Veldhuis and Eitelberg17). This problem was solved numerically, and results compared sufficiently well to the aforementioned experiment(Reference Van Der Wall18).

Figure 2. Possible vortex orientation relative to the helicopter main and tail rotor. (a) Longitudinal vortex: longitudinal in the main and in the tail rotor. (b) Lateral vortex: lateral in the main rotor, normal in the tail rotor. (c) Orthogonal vortex: normal in the main rotor, lateral in the tail rotor.
In general, the vortices encountered by rotor blades can have a large variety of sizes, as pointed out by McCormick(Reference Mccormick19). The scale can best be represented by the vortex core radius made non-dimensional by the interacting rotor blade radius: rc =Rc/R. Tail rotor blade tip vortices can be immersed into the main rotor disk and can be assumed to be very small. Next, and about 5 times larger, are vortices of the classical blade-vortex interaction problem, with vortices generated at the front of the rotor disk and interacting with blades in the first and fourth quadrant, where rc ≈ 0.006 − 0.01. The main rotor vortices that travel across the tail rotor, which are usually generated just ahead of it, were measured(Reference Yin, Van Der Wall and Oerlemans20) with rc ≈ 0.02. Main and tail rotor interactions with ground vortices are a scale one order of magnitude larger: measurements revealed rc ≈ 0.25 for the main rotor and rc ≈ 1.25 for the tail rotor. The aforementioned orthogonal interaction of a wing tip vortex and a propeller(Reference Yang, Zhou, Sciacchitano, Veldhuis and Eitelberg17) contained a non-dimensional vortex size of rc ≈ 0.082.
In this article, rotors of different sizes are subjected to a vortex of a large virtual 7 MW WT at a moderate distance of 100 m to it. The vortex is then relatively young (i.e., the circulation is strong and the core size is small). These are: a Bo105 helicopter main rotor (BoMR), a representative ultra-light sports autogyro (AG) rotor (4/5th of the Bo105 main rotor size), a representative ultra-light coaxial (COAX) helicopter rotor (3/5th), and the Bo105 tail rotor (BoTR; 1/5th). While the BoMR is of the hingeless type, all others are teetering rotors. Additionally, the BoTR includes a pitch-flap coupling by a δ 3 hinge. Their characteristics vary in terms of their mechanical parameters such as blade Lock number γ and natural frequency of flapping vβ and in their aerodynamic parameters such as solidity σ and blade tip speed U.
2.0 TECHNICAL APPROACH
Because a typical WT rotor blade radius is about 15 times larger than the BoMR blade radius, the curvature of the WT wake within the encountering rotor’s disk can be ignored and a straight vortex is used. For ease of computation this straight vortex is infinitely long, Fig. 2. This equivalent straight line vortex circulation strength Γeq was estimated from the swirl velocity field at the top of the wake spiral and was found to be roughly half of the WT vortex circulation Γ(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21). For the swirl velocity profile the Vatistas model(Reference Vatistas, Kozel and Mih22) was used, which allows analytic solutions for the rotor blade air loads in the case of longitudinal and lateral vortex orientation, Fig. 2(a) and (b), while the orientation normal to the rotor disk Fig. 2(c) was evaluated numerically.
Blade element theory is applied for the rotor blade aerodynamics, with the assumption of two-dimensional incompressible steady linear aerodynamics at the blade elements and a constant drag coefficient. First, the rotor is trimmed to the desired thrust and zero hub moments in undisturbed air. In the case of the helicopter, a propulsive force trim is performed with a constant drag area representing the fuselage and collective, longitudinal and lateral cyclic controls as well as rotor shaft angle of attack used for trimming. In the case of the BoTR, it is trimmed to the desired thrust by collective control only, leaving a cyclic flapping motion. The AG rotor has a fixed collective control setting and no cyclic controls, but the shaft angle of attack is varied until the desired thrust is obtained. This also includes some longitudinal flapping as a result. The available control margin is defined as the difference between the maximum possible control deflection and the control used for trimming. Similarly, the flapping margin is defined as the difference between the flapping resulting from the trim and the maximum possible flapping deflection (which can be touching the blade stops at the shaft, touching the tail boom, or blades colliding with each other in case of a COAX rotor).
Then the vortex is included. While the longitudinal oriented vortex is placed at different lateral positions all across the rotor disk, the lateral vortex is placed at different longitudinal positions. The vortex orientation normal to the disk is placed at the hub center in longitudinal direction and at different lateral positions all across the rotor disk. For any of these configurations the shaft angle remains unchanged and a retrim of the rotor is performed to compute the control perturbations needed to retrim, which can be divided by the available control margin. This is called the rotor control ratio RCR. A value of 1 means that all available margin is consumed by retrimming, and nothing is left which is considered dangerous. Alternatively, no pilot actions are performed and the amount of flapping developing due to the vortex influence is computed. These flapping perturbations then can be related to the available flapping margin, and that ratio is called the rotor flapping ratio RFR. Again, a value of 1 means that all flapping margin is consumed and rotor blades touching blade stops, the tail boom, or other rotor blades are the next thing to happen.
The basic concept of blade element theory is based on the velocity components acting at the blade section of interest in the plane of rotation (= tangential velocity), VT, and perpendicular to it (= normal velocity), VP. Depending on the vortex orientation with its axis in the rotor disk (longitudinal, lateral) or normal to it (orthogonal), it generates perturbations in the normal velocity ΔVP, or in the tangential velocity ΔVT, respectively, which add to the components during operation in undisturbed air V T0, V P0. Thus, with the non-dimensional time derivative * = d/(Ωdt)
 $$
\matrix{
{V_T } \hfill & = \hfill & {V_{T0} + \Delta V_T ;\quad \quad V_{T0} = r + \mu \sin \psi ;\quad \quad \mu = V_\infty \cos \alpha _S /U} \hfill \cr
{V_P } \hfill & = \hfill & {V_{P0} + \Delta V_P ;\quad \quad V_{P0} = \mu _z + \lambda _i + \mu \beta \cos \psi + r\mathop \beta \limits^* ;\quad \quad \mu _z = - \mu \tan \alpha _S } \hfill \cr
{\Delta V_T } \hfill & = \hfill & {\lambda _V {{\left| {x - x_0 } \right|\cos \psi + \;{\rm{s}}gn\;\left( {x - x_0 } \right)\left( {y - y_0 } \right)\sin \psi } \over {\sqrt {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 } }}} \hfill \cr
{\Delta V_P } \hfill & = \hfill & {\Delta \lambda _i + r\Delta \mathop \beta \limits^* + \lambda _V ;\quad \quad \lambda _V = \lambda _{V0} {{\sqrt {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 } } \over {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 + r_c^2 }}} \hfill \cr } $$
$$
\matrix{
{V_T } \hfill & = \hfill & {V_{T0} + \Delta V_T ;\quad \quad V_{T0} = r + \mu \sin \psi ;\quad \quad \mu = V_\infty \cos \alpha _S /U} \hfill \cr
{V_P } \hfill & = \hfill & {V_{P0} + \Delta V_P ;\quad \quad V_{P0} = \mu _z + \lambda _i + \mu \beta \cos \psi + r\mathop \beta \limits^* ;\quad \quad \mu _z = - \mu \tan \alpha _S } \hfill \cr
{\Delta V_T } \hfill & = \hfill & {\lambda _V {{\left| {x - x_0 } \right|\cos \psi + \;{\rm{s}}gn\;\left( {x - x_0 } \right)\left( {y - y_0 } \right)\sin \psi } \over {\sqrt {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 } }}} \hfill \cr
{\Delta V_P } \hfill & = \hfill & {\Delta \lambda _i + r\Delta \mathop \beta \limits^* + \lambda _V ;\quad \quad \lambda _V = \lambda _{V0} {{\sqrt {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 } } \over {\left( {x - x_0 } \right)^2 + \left( {y - y_0 } \right)^2 + r_c^2 }}} \hfill \cr } $$
All velocities are made non-dimensional by the rotor blade tip speed U = ΩR. For simplicity, the thrust-induced inflow ratio λi is assumed as constant over the rotor disk. This is appropriate because in this study only rotor control perturbations relative to a trim in undisturbed air are of interest, not the trim itself. In case of no retrim the thrust will change and with it the mean induced inflow, but the flapping perturbations are mainly depending on the change of thrust and mean inflow. The thrust-induced inflow perturbation is nonlinearly depending on the thrust coefficient and linearised about the trim thrust as follows(Reference Van Der Wall and Lehmann23):
 $$
\matrix{
\hfill {\Delta \lambda _i } & \hfill = & \hfill {{{d\lambda _{i0} } \over {dC_T }}\Delta C_T ;\quad \lambda _{i0} = \sqrt {\sqrt {{{C_T^2 } \over 4} + {{\mu ^4 } \over 4}} - {{\mu ^2 } \over 2}} } \cr
\hfill {{{d\lambda _{i0} } \over {dC_T }}} & \hfill = & \hfill {{{C_T } \over {\sqrt 8 \sqrt {\sqrt {C_T^2 + \mu ^4 } - \mu ^2 } \sqrt {C_T^2 + \mu ^4 } }}} \cr } $$
$$
\matrix{
\hfill {\Delta \lambda _i } & \hfill = & \hfill {{{d\lambda _{i0} } \over {dC_T }}\Delta C_T ;\quad \lambda _{i0} = \sqrt {\sqrt {{{C_T^2 } \over 4} + {{\mu ^4 } \over 4}} - {{\mu ^2 } \over 2}} } \cr
\hfill {{{d\lambda _{i0} } \over {dC_T }}} & \hfill = & \hfill {{{C_T } \over {\sqrt 8 \sqrt {\sqrt {C_T^2 + \mu ^4 } - \mu ^2 } \sqrt {C_T^2 + \mu ^4 } }}} \cr } $$
The magnitude of the vortex-induced contribution is ![]() $$ \lambda _{V0} = \Gamma _{eq} /\left( {2\pi UR} \right) $$, which represents a non-dimensional circulation, and the maximum vortex-induced velocity is obtained at the vortex core radius.
$$ \lambda _{V0} = \Gamma _{eq} /\left( {2\pi UR} \right) $$, which represents a non-dimensional circulation, and the maximum vortex-induced velocity is obtained at the vortex core radius.
For a constant vortex circulation, the non-dimensional magnitude thus depends on the rotor tip speed and its radius. For constant tip speed, this depends only on the radius. Small rotors will therefore experience a larger relative disturbance than large rotors. The non-dimensional peak vortex-induced velocity λV,max is constant for constant rotor tip speed independent of its radius, but grows for smaller tip speeds. The rotor control consists of the built-in pretwist, the pilot controls in collective, longitudinal and lateral cyclic, and its perturbations (TR: no cyclic controls; AG: fixed collective only). Similarly, the blade flapping consists of precone, coning, longitudinal and lateral cyclic flapping (see-saw rotors: no coning).
 $$
\matrix{
\hfill \Theta & \hfill = & \hfill {\Theta _{trim} + \Delta \Theta } \cr
\hfill {\Theta _{trim} } & \hfill = & \hfill {\Theta _{tw} \left( {r - 0.75} \right) + \Theta _0 + \Theta _C \cos \psi + \Theta _S \sin \psi } \cr
\hfill {\Delta \Theta } & \hfill = & \hfill {\Delta \Theta _0 + \Delta \Theta _C \cos \psi + \Delta \Theta _S \sin \psi } \cr
\hfill \beta & \hfill = & \hfill {\beta _{trim} + \Delta \beta } \cr
\hfill {\beta _{trim} } & \hfill = & \hfill {\beta _P + \beta _0 + \beta _C \cos \psi + \beta _S \sin \psi } \cr
\hfill {\Delta \beta } & \hfill = & \hfill {\Delta \beta _0 + \Delta \beta _C \cos \psi + \Delta \beta _S \sin \psi } \cr
\hfill {} & \hfill {} & \hfill {} \cr } $$
$$
\matrix{
\hfill \Theta & \hfill = & \hfill {\Theta _{trim} + \Delta \Theta } \cr
\hfill {\Theta _{trim} } & \hfill = & \hfill {\Theta _{tw} \left( {r - 0.75} \right) + \Theta _0 + \Theta _C \cos \psi + \Theta _S \sin \psi } \cr
\hfill {\Delta \Theta } & \hfill = & \hfill {\Delta \Theta _0 + \Delta \Theta _C \cos \psi + \Delta \Theta _S \sin \psi } \cr
\hfill \beta & \hfill = & \hfill {\beta _{trim} + \Delta \beta } \cr
\hfill {\beta _{trim} } & \hfill = & \hfill {\beta _P + \beta _0 + \beta _C \cos \psi + \beta _S \sin \psi } \cr
\hfill {\Delta \beta } & \hfill = & \hfill {\Delta \beta _0 + \Delta \beta _C \cos \psi + \Delta \beta _S \sin \psi } \cr
\hfill {} & \hfill {} & \hfill {} \cr } $$
From the velocity components, the blade flapping, the controls, and the shaft angle of attack the blade lift, the blade aerodynamic moment about the hub and the blade torque can be computed by integration over the aerodynamically effective part of the blade.
 $$
\matrix{
\hfill {\overline L } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B V_T^2 \Theta - V_T V_P dr = {1 \over 2}\int\limits_A^B \left( {V_{T0} + 2V_{T0} \Delta V_T + \Delta V_T^2 } \right)\left( {\Theta _{trim} + \Delta \Theta } \right)} \cr
\hfill {} & \hfill {} & \hfill { - \left( {V_{T0} + \Delta V_T } \right)\left( {V_{P0} + \Delta V_P } \right)dr} \cr
\hfill {\overline {M_\beta } } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left( {V_T^2 \Theta - V_T V_P } \right)dr} \cr
\hfill {\overline Q } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left( {V_T^2 \Theta - V_T V_P } \right){{V_P } \over {V_T }} + rV_T^2 {{C_{d0} } \over {C_{l\alpha } }}dr} \cr
\hfill {} & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left[ {\left( {V_{T0} + \Delta V_T } \right)\left( {V_{P0} + \Delta V_P } \right)\left( {\Theta _{trim} + \Delta \Theta } \right) - \left( {V_{P0} + \Delta V_P } \right)^2 } \right]dr} \cr
\hfill {} & \hfill {} & \hfill { + {\kern 1pt} {1 \over 2}\int\limits_A^B r\left( {V_{T0} + 2V_{T0} \Delta V_T + \Delta V_T^2 } \right){{C_{d0} } \over {C_{l\alpha } }}dr} \cr }$$
$$
\matrix{
\hfill {\overline L } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B V_T^2 \Theta - V_T V_P dr = {1 \over 2}\int\limits_A^B \left( {V_{T0} + 2V_{T0} \Delta V_T + \Delta V_T^2 } \right)\left( {\Theta _{trim} + \Delta \Theta } \right)} \cr
\hfill {} & \hfill {} & \hfill { - \left( {V_{T0} + \Delta V_T } \right)\left( {V_{P0} + \Delta V_P } \right)dr} \cr
\hfill {\overline {M_\beta } } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left( {V_T^2 \Theta - V_T V_P } \right)dr} \cr
\hfill {\overline Q } & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left( {V_T^2 \Theta - V_T V_P } \right){{V_P } \over {V_T }} + rV_T^2 {{C_{d0} } \over {C_{l\alpha } }}dr} \cr
\hfill {} & \hfill = & \hfill {{1 \over 2}\int\limits_A^B r\left[ {\left( {V_{T0} + \Delta V_T } \right)\left( {V_{P0} + \Delta V_P } \right)\left( {\Theta _{trim} + \Delta \Theta } \right) - \left( {V_{P0} + \Delta V_P } \right)^2 } \right]dr} \cr
\hfill {} & \hfill {} & \hfill { + {\kern 1pt} {1 \over 2}\int\limits_A^B r\left( {V_{T0} + 2V_{T0} \Delta V_T + \Delta V_T^2 } \right){{C_{d0} } \over {C_{l\alpha } }}dr} \cr }$$
This equation reveals that disturbances ΔVP generated by an in-plane vortex orientation (longitudinal, lateral) are linearly affecting the blade lift and the aerodynamic moment about the hub(Reference Van Der Wall and Van Der Wall15,Reference Van Der Wall16) , while disturbances generated by an orthogonal vortex orientation ΔVT have a non-linear effect, at least from a mathematical point of view(Reference Van Der Wall18). However, in most cases the peak vortex-induced velocities of WTs are in the order of 10 m/s(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21), while typical helicopter blade tip speeds are around 220 m/s. At the representative radius of r = 0.75 they are still around 165 m/s, more than one order of magnitude larger. Therefore, the term ![]() $$ \Delta V_T^2 $$ is found negligibly small relative to the other terms in the respective parenthesis and can be ignored, rendering the orthogonal vortex influence also to be linear in the lift(Reference Van Der Wall18). Additionally, the influence of ΔVP on lift can be computed independent of the trim, because V T0 is independent of the trim since the rotor shaft angle of attack remains unchanged. The influence of ΔVT depends on the trim itself via the products
$$ \Delta V_T^2 $$ is found negligibly small relative to the other terms in the respective parenthesis and can be ignored, rendering the orthogonal vortex influence also to be linear in the lift(Reference Van Der Wall18). Additionally, the influence of ΔVP on lift can be computed independent of the trim, because V T0 is independent of the trim since the rotor shaft angle of attack remains unchanged. The influence of ΔVT depends on the trim itself via the products ![]() $$ \Delta V_T \Theta _{trim} $$ and
$$ \Delta V_T \Theta _{trim} $$ and ![]() $$ \Delta V_T V_{P0} $$, where the latter contains βtrim. From Eq. (1) it can also be seen that all of the vortex-induced velocities of the in-plane vortex orientation enter the blade lift, while only a fraction of it contribute to ΔVT. From these plausibility considerations it can already be concluded that in-plane vortex orientations will have a larger impact on blade lift than an orthogonal vortex orientation. The vortex influence on rotor torque always depends on the trim of the rotor due to the coupling of perturbations with the trim solution (see lower part of Eq. (5)). The non-dimensional blade flapping equation of motion is
$$ \Delta V_T V_{P0} $$, where the latter contains βtrim. From Eq. (1) it can also be seen that all of the vortex-induced velocities of the in-plane vortex orientation enter the blade lift, while only a fraction of it contribute to ΔVT. From these plausibility considerations it can already be concluded that in-plane vortex orientations will have a larger impact on blade lift than an orthogonal vortex orientation. The vortex influence on rotor torque always depends on the trim of the rotor due to the coupling of perturbations with the trim solution (see lower part of Eq. (5)). The non-dimensional blade flapping equation of motion is ![]() $$ [** = d^2 /\left( {\Omega dt} \right)^2 ] $$
$$ [** = d^2 /\left( {\Omega dt} \right)^2 ] $$
All the mathematics to compute aerodynamic hub moments, rotor thrust and power, perturbations in thrust-induced velocity, and blade flapping response equations are not repeated here since they were completely given in prior publications(Reference Van Der Wall and Van Der Wall15,Reference Van Der Wall16,Reference Van Der Wall18,Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21) .
3.0 WIND TURBINE AND ROTORCRAFT DATA
An example WT of 7 MW power rating is used here, because some WTs of that power class are already installed onshore in Germany. Its blade radius is as RWT = 77 m with three blades and a solidity of σ = 0.0285 in an operating condition where the maximum blade circulation is generated(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21), which happens at a wind speed of about VW = m/s. At a distance of 100 m downstream of the turbine, vortex aging(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21) has reduced the tip vortex circulation only slightly, but the initial core radius is already significantly increased to Rc = 0.542 m. The equivalent circulation of an infinitely long straight-line vortex generating the same swirl velocity profile as the WT spiral vortex was estimated to Γeq = 51.8 m2/s, with a peak vortex-induced velocity of 7 m/s at the core radius. The vortex-encountering rotors investigated are given in Table 1 with their characteristic data. Due to the higher blade tip Mach numbers, the lift curve slope and drag coefficient are taken little larger for the BoMR and BoTR than for the AG and COAX helicopter rotors.
Table 1 Rotor data and non-dimensional vortex parameters

Based on the rotor data the non-dimensional vortex data can be computed and are given at the end of Table 1. Although the physical core radius is the same throughout, the non-dimensional core radius rc is smallest for the largest rotor and highest for the smallest rotor. This parameter represents the radial range of the rotor blade covered by the vortex core radius. From this it is expected that the smallest rotor receives the largest relative increment in lift due to the vortex influence, and thus the largest control perturbations might be needed to mitigate vortex effects. With respect to the blade flapping response the Lock number is the multiplier to the non-dimensional aerodynamic flapping moment, thus the product γλ V0 is representative for the flapping excitation (Eq. (6)), as long as the natural flapping frequency is ignored. This product is similar for the BoMR and the representative AG rotor, but 50% larger for the COAX rotor and BoTR.
The radial distribution of vortex-induced velocity vV is shown in Fig. 3(a) and is based on the vortex parameters given before. In addition the rotorcraft blade geometries are sketched in proportion to get an impression of the size relation of the vortex core radius and the blade radii.

Figure 3. Vortex swirl velocity profile. (a) Swirl velocity and rotor blade sizes. (b) Non-dimensional swirl on blade surfaces.
Figure 3(b) shows the same swirl velocity distribution over their respective blade spans as in (a), but now the swirl is made non-dimensional with the respective tip speed, and the radial coordinate is made non-dimensional with the respective rotor radius. Due to the higher tip speed of the Bo105 rotor (with respect to the AG and the COAX rotors), the relative vortex influence is lower than for the other rotor examples. The different lengths of the blades also lead to differences: While the BoTR is affected over its entire span with the maximum swirl, all other blades experience much more radial decay of the swirl profile given in Fig. 3(a). Due to the different tip speeds, the AG and the COAX rotors experience higher non-dimensional peak swirl velocities. The lowest impact can be expected for the Bo105 main rotor blade, because of its high tip speed and its large radius. These relations are useful for judgement of the pilot control magnitudes required to mitigate the vortex impact on trim.
For the second problem, the judgement of blade flapping deflections, the Lock number is a multiplier as seen in Eq. (6) on the right hand side. The resulting velocity distributions are given in Fig. 4(a). Based on this representation, the vortex impact on flapping response of the COAX rotor can be expected to be the largest. To a less degree the AG and the BoMR are rather similarly affected by the vortex, and the smallest impact can be assumed for the BoTR due to its small Lock number. This is caused by its large blade inertia related to the blade aerodynamic characteristics. In addition, the magnitude of the dynamic flapping response is dependent on the natural frequency of the blade, and both Bo105 rotors have an effective natural frequency of flapping significantly higher than 1. For the BoMR, the reason is the hingeless blade attachment with its blade root stiffness, and for the BoTR it is the pitch-flap coupling, that introduces the stiffness via aerodynamic forces. The other rotors are centrally hinged and thus in resonance with the rotation. Equation (6) also indicates that the (steady) flapping response will be inverse to the square of the effective natural frequency in flapping, and the additional weighing of the inflow distribution with this parameter is shown in Fig. 4(b). Then, a clear hierarchy is indicated: the largest excitation will be expected for the COAX system, followed by the AG, then the BoMR and least for the BoTR.

Figure 4. Swirl velocity distributions with different weighting. (a) Lock number weighted. (b) Related to flapping frequency.
In order to evaluate the control and flapping margins available, the maximum control and flapping deflections need to be known along with the control and flapping deflections during trimmed flight. For the Bo105, the trim data is taken from flight tests and documentation available from GARTEUR activities(Reference Dequin, Von Grünhagen, Haddon, Haverdinks, Kampa, Mccallum, Padfield and Weinstock24), and data from a representative ultralight COAX helicopter flight test has recently been published(Reference Feil, Rinker and Hajek25); the control limits of it are based on personal communication. For the representative AG flight trim data from DLRs experimental vehicle were taken based on a MTOsport 2010(Reference Duda and Seewald26). In former publications, the available margin for combined collective and cyclic control was assumed as 8 deg for the BoMR and 15 deg for combined coning and cyclic flapping, both independent of the flight situation(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21,Reference Van Der Wall and Lehmann23) . A more precise estimate of available margins has to take into account the amount of controls and flapping already occurring in trimmed flight, and the smaller distance to upper or lower bounds of the respective control or flapping represents the actually available margin at that respective flight condition. These control and flapping limits are given in Table 2. Of main importance are the collective control, the longitudinal cyclic controls, and the longitudinal flapping, as well as the BoTR collective (no cyclic controls available here) and the mast pitch in case of the AG (no blade controls at all).
Table 2 Rotor control and flapping limits

The available margin requires knowledge of the trim condition, the controls required, and the flapping developing therein. This data is given in Fig. 5 for the various rotorcraft of interest. The left column includes the trim data (controls and flapping) during level flight for the BoMR and BoTR in (a), for the AG in (c) and for the COAX rotor in (e). The right column displays the resulting control and flapping margins based on the boundaries given in Table 2. The physical cause of the limits is different for the various rotorcrafts. While for the BoMR the longitudinal flapping limit is driven by the blades striking the fuselage (lateral flapping can be much larger without collisions), the BoTR may first reach the blade stops at its shaft, resulting in its equivalent of mast bumping or by striking the fuselage, whichever comes first. The AG may experience either mast bumping or the blades hitting the empennage, whichever comes first. In case of the COAX rotor mast bumping may be one limit when both counter-rotating rotors tilt in parallel. Usually, the coaxial rotor blades are colliding due to differential cyclic flapping, which is confined by the rotor separation distance.

Figure 5. Rotor controls and margins during trimmed level flight. (a) BoMR and BoTR trim. (b) BoMR and BoTR control and flapping margins. (c) AG main rotor trim. (d) AG main rotor control and flapping margins. (e) COAX rotor trim. (f) COAX rotor control and flapping margins.
Control limits may be reached in collective (BoMR and BoTR, COAX rotor) or cyclic controls (BoMR and COAX rotor) or in the rotor shaft pitch angle in case of the AG. The right column of Fig. 5 shows how the control margins vary with the advance ratio for this level flight trim (at sea level). With greater height the control angles will vary relative to flight at sea level, and accordingly the margins will shrink. In former publications(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21,Reference Van Der Wall and Lehmann23) it was shown that the vortex impact on controls and flapping is growing with flight speed. Therefore, an advance ratio of μ = 0.3 has been chosen here for the further results. Because at this advance ratio the margins shrink due to large trim deflections required, this is considered the most adverse condition for a vortex encounter. The control margins at μ = 0.3 are summarised in Table 3.
Table 3 Control and flapping margins at μ = 0.3

4.0 RESULTS
4.1 Controls required for retrimming the rotor, longitudinal vortex orientation
A longitudinal vortex orientation occurs when flying across the upper part of the WT wake as sketched in Fig. 1 and Fig. 2(a). This can be considered as quasi-steady because the vortex will remain in the rotor for some time. First, pilot controls required to mitigate the vortex impact on the rotor trim are computed. The trim here is defined as the prescribed rotor thrust and zero hub moments for shaft-driven rotors (this allows for a change of rotor power). The AG trim is defined here as zero shaft power and zero hub moments (this allows for a change of thrust). For the BoMR and for the COAX (individual) rotor, the controls are the collective, the longitudinal and the lateral cyclic control angles. However, this is confined to one of the two rotors only, and not applicable in reality because both rotors are rotating in opposite sense, therefore are reacting to the vortex in opposition, and would require a differential cyclic control to mitigate the vortex impact. Therefore, the cyclic controls are for an isolated rotor only, rotating in the same sense as the BoMR. The BoTR is operated by its collective control angle only, because its swashplate cannot be tilted. Last, the AG is controlled by tilting the rotor mast, and in addition mainly longitudinal flapping will occur.
These control perturbations relative to the trim are given in Fig. 6(a) for the collective control angle (AG: shaft angle instead as equivalent) and for the change of rotor coning in just the case of the BoMR (all other rotors are teetering and an elastic coning is not considered). The AG shaft angle required is larger than the collective controls of the other rotors because the thrust increase due to one degree of shaft angle is about half of the thrust increase due to one deg of collective control angle. However, in case of the AG zero power is the trim goal for keeping the autorotation at constant rotor speed of rotation, which allows for a change of rotor thrust, while the other rotors keep the thrust constant and thus allowing a change of the rotor power. The BoTR collective variation is smoother, because the vortex swirl field has a much larger wavelength relative to the blade span when compared to the other rotors, see Fig. 3(b). Figure 6(b) shows the longitudinal control angle required for retrimming (AG: longitudinal flapping angle; TR: longitudinal and lateral flapping angle – both rotors do not have cyclic control available). Both the BoMR and the COAX rotor are retrimmed via collective and cyclic control angles, thus their curve shape of these controls is quite similar. However, the BoMR requires less control input because the vortex disturbance is less relative to the blade length as already seen in Fig. 3(b). Also, the AG longitudinal flapping ΔβC developing during the retrim is of the same order as ΔΘC of the COAX rotor. Because the BoTR has a much smaller Lock number than the other rotor blades, its cyclic flapping response is smaller in magnitude. Due to a natural frequency significantly higher than unity, both lateral and longitudinal flapping of similar magnitude develops.

Figure 6. Rotor control perturbations required for retrimming the rotor. (a) Collective control and rotor coning; AG: shaft tilt (b) Longitudinal cyclic controls; AG+TR: cyclic flapping.
Next, these non-dimensional perturbations are converted to physical units and then divided by the available and respective control margins for an advance ratio of μ = 0.3 given in Table 3. The result is the rotor control ratio RCR = ΔΘ/ΔΘmax and the rotor flapping ratio RFR = Δβ/Δβmax shown in Fig. 7(a) for the collective control (AG: shaft angle instead) and in (b) for the longitudinal cyclic control angle. RCR or RFR values up to 0.5 are considered controllable or acceptable, but values higher than 0.7 are rated as dangerous(Reference Van Der Wall, Fischenberg, Lehmann and Van Der Wall21). An RCR > 1 means that the disturbance cannot be retrimmed anymore, and an RFR > 1 means a collision of rotor blades with the fuselage or rotor shaft (COAX rotor: with blades of the other rotor) does happen with fatal consequences. The influence of the available margin left after trimming the rotor is of highest importance here: in case of the COAX rotor the available margin in collective control angle is small (see Table 3) and thus the required collective control to mitigate the vortex influence is exceeding that margin for vortex positions at the right and left of the rotor disk. The BoMR reaches RCR = 0.6 when the vortex is at the retreating side of the rotor disk, which leaves little room for further maneuvering or for stronger vortex disturbance mitigation. In case of the AG even a value of 0.8 is reached, which means the shaft angle is close to its mechanical limits.

Figure 7. Rotor control and flapping ratio during retrim, longitudinal vortex. (a) RFR of longitudinal flapping angle and rotor coning (BoMR only). (b) RFR of lateral flapping angle.
The cyclic control RCR values are shown in Fig. 7(b) for the BoMR and the COAX rotor only (the AG and BoTR do not have cyclic control). For the BoMR, values of 0.4 are reached leaving enough room for stronger disturbances, but the COAX rotor cyclic control RCR reaches a value of 0.8, close to its mechanical limits that are reached at RCR = 1. However, it must be kept in mind that cyclic control cannot be used in the COAX rotor for mitigation of vortex effects, because differential cyclic control would be needed. Therefore, this is only a hypothetical single rotor value for purposes of comparison only. Finally, the RFR values of the AG and BoTR are given in Fig. 7(c), together with the respective values of the BoMR coning and also the BoTR lateral flapping. Except for the AG all values are found uncritical, the AG longitudinal flapping reaches RFR = 0.8 for a vortex position in the hub center, leaving little room for further flapping.
4.2 Rotor flapping developing without retrimming the rotor, longitudinal vortex orientation
When no pilot action is performed, the induced velocities of the vortex will change the aerodynamic thrust and the aerodynamic lateral flapping moment. The rotor blade will respond depending on its dynamic characteristics following Eq. (6), expressed by its effective natural frequency of flapping vβeff and its Lock number γ given in Table 1. The longitudinal flapping reaction is shown in Fig. 8(a) for all the rotors, also including the coning reaction of the BoMR. The largest reactions are found for the AG and COAX rotors, while the BoMR and BoTR both have an effective natural frequency significantly higher than one, and the BoTR in addition a much smaller Lock number, consequently with smaller flapping magnitude. Lateral flapping is shown in Fig. 8(b), which develops for the BoMR and BoTR. The BoTR reaction is of similar size as in longitudinal flapping, while the BoMR has less lateral than longitudinal flapping, because its natural frequency is closer to one than for the BoTR.

Figure 8. Cyclic flapping developing when no pilot action is performed, longitudinal vortex. (a) Longitudinal flapping angle and rotor coning (BoMR only) (b) Lateral flapping angle.
After division by the available flapping margins at this operational condition the RFR as shown in Fig. 9 is resulting. Only the AG and COAX rotors reach values around 0.7, leaving only little margin for larger disturbances. For the other rotors the margins are larger and the deflections smaller, such that the RFR values remains uncritical small.

Figure 9. Rotor flapping ratio developing when no pilot action is performed, longitudinal vortex. RFR of longitudinal flapping angle and rotor coning (BoMR only). RFR of lateral flapping angle.
4.3 Rotor power and thrust variations
Retrimming the rotors for constant thrust and zero hub moments is associated with power variations of significant amount(Reference Van Der Wall and Lehmann23). When the AG kees the power and the hub moments at zero, the result is variation in thrust. In case when no pilot actions are performed for retrimming, the rotor reaction to the vortex swirl field causes both thrust and power variations. These are shown in Fig. 10(a) when retrimming the rotors. Vortex positions to the left of the disk, inducing downwash all over the disk, require more power than in undisturbed air. In contrast, vortex positions to the right of the disk, inducing upwash, require less power. In case of the AG the thrust variation is shown and the downwash causes a loss of thrust, while the upwash and increase.

Figure 10. Rotor power and thrust variations developing when no pilot action is performed, longitudinal vortex. (a) Power variation during retrim. (b) Thrust variation without retrim.
Figure 10(b) provides the thrust variation for all rotors in case of no pilot action for retrimming is performed. It is obvious that all rotors experience significant variations, the largest ones found in the COAX rotor as already suggested in conjunction with Fig. 4(b). Especially for teetering rotors without a pitch-flap coupling, such as the AG and COAX rotors, a loss of thrust means rotor unloading, or “low g” conditions, that have to be avoided, because of loss of rotor control in the rotorcraft pitch and roll axis. On the other hand, large power variations may also significantly affect the flight mechanics, because in high speed flight the available excess power is very limited and surely less than 40% reached here due to the vortex influence (this is not further investigated here).
4.4 Lateral vortex orientation
A lateral vortex orientation occurs when flying along the upper part of the WT wake in Fig. 1 against the wind direction towards the WT or with the wind downstream away from it. The vortex is then lateral within the main rotor disk as sketched in Fig. 2(b), while it is normal to the disk for the tail rotor. This essentially is an unsteady passage, but is treated here as quasi-steady and thus the results will be over-conservative; the unsteady passage of the vortex will cause less rotor reaction because only transient reactions will occur. While the longitudinal vortex orientation treated in the section before induces a lateral asymmetry of vortex-induced velocities and associated loads, its induced velocities are symmetric in longitudinal direction and the associated loads as well, because the dynamic pressure is the same at the blades in the front and aft position. This is different for the lateral vortex orientation, which induces a longitudinal asymmetry of velocities and associated loads, but the lateral vortex-induced loads are not symmetric despite the symmetry of vortex-induced velocities, because the dynamic pressure on the advancing and retreating blade is different in forward flight.
Results are given here for the main contributions to the RCR development during retrim in Fig. 11, which may be compared to the results shown in Fig. 7 for the longitudinal vortex. In general, the RCR peak values are found about 0.1 smaller than those of the longitudinal vortex, and the reason is that the lateral asymmetry of induced velocities caused by the longitudinal vortex are exaggerated by the lateral asymmetry of dynamic pressure in forward flight, while the longitudinal asymmetry of vortex-induced velocities is much less affected.
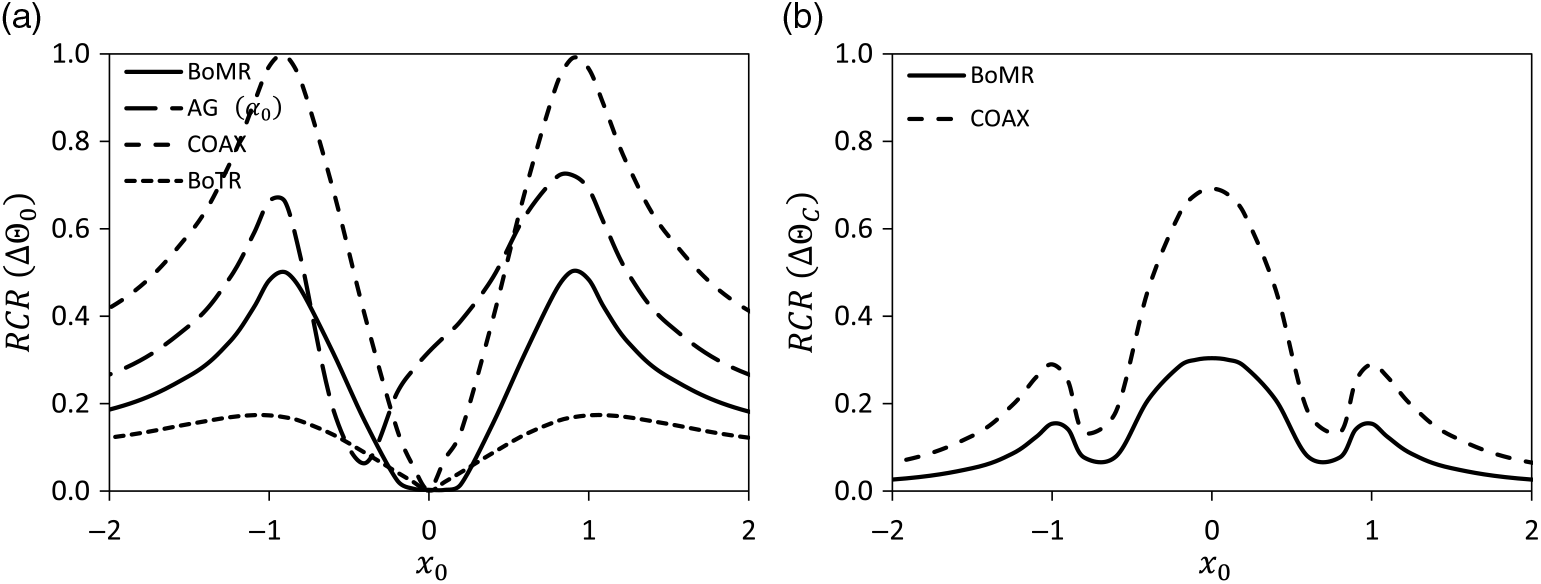
Figure 11. Rotor control and flapping ratio during retrim, lateral vortex. (a) RCR for collective control angle (AG: shaft angle). (b) RCR for lateral cyclic control angle.
In case of no retrim, the RFR developing is given in Fig. 12, to be compared with Fig. 9. Because the vortex orientation has changed by 90 deg relative to the longitudinal vortex, it is the lateral flapping which develops largest amplitudes, and according to the margins given in Table 3 the RFR is also largest for this flapping direction. Again the peak values are less than for the longitudinal vortex for the same reasons as explained before.

Figure 12. Rotor flapping ratio developing when no pilot action is performed, lateral vortex. (a) RFR of longitudinal flapping angle. and rotor coning (BoMR only). (b) RFR of lateral flapping angle.
Finally, the power variations during retrim and the thrust variations developing when no retrim is performed are shown in Fig. 13, to be compared with Fig. 10 from the investigation of the longitudinal vortex. An essentially similar behaviour is seen in the respective graphs of both figures, which is because in either cases the vortex enters the rotor with its downwash field first and leaves it with its upwash field.

Figure 13. Rotor power and thrust variations developing when no pilot action is performed, lateral vortex. (a) Power variation during retrim. (b) Thrust variation without retrim.
4.5 Orthogonal vortex orientation
In this case the vortex axis is perpendicular to the rotor disk, which happens for the BoTR when the helicopter is flying along the top of the wake towards the WT or away from it, Fig. 1. Also, this occurs for the BoMR when flying at half height across the WT wake and this is sketched in Fig. 2(c). This condition can be quasi-steady when hovering in the vortex, but in forward flight the vortex passes across the disk and its phenomena will be unsteady. With an advance ratio of 0.3 the treatment in quasi-steady manner is thus over-conservative.
A fundamental difference between the orthogonal vortex orientation and both the longitudinal and lateral orientations is that the vortex-induced velocities are within the plane of the rotor disk for the former, and normal to it for the latter. Therefore, the orthogonal vortex first adds to the blade element tangential velocities (and thus the local dynamic pressure), and second contributes to the radial velocities that do not enter the two-dimensional aerodynamics. Due to this, only a fraction of its induced velocities enter the dynamic pressure and with it the blade elements lift. Also, because the maximum vortex swirl velocity usually is one order of magnitude less than the circumferential velocity of the blade, its influence on the total dynamic pressure and thus local lift can be expected as rather small. Both the longitudinal and lateral vortex orientation induce velocities normal to the rotor disk, thus directly cause local angle of attack variations to a significant amount, because the vortex peak swirl velocities are of the same order of magnitude as the other normal velocities occurring in flight.
The treatment of the orthogonal vortex-rotor interaction is more involved than that of the longitudinal or lateral vortex orientations(Reference Van Der Wall18). An interesting condition is a vortex axis centered in the rotor hub. Depending on its swirl direction the vortex-induced velocities either add everywhere to the circumferential velocities, thus increasing the dynamic pressure everywhere and hence the rotor thrust, or they reduce the circumferential velocities. This latter condition is aerodynamically similar to a reduced rotor speed of rotation and associated with a loss of thrust. At the extreme, a very strong vortex therefore can lead to a zero dynamic pressure in average, with a total loss of lift, whatever collective control is applied, and therefore with a total loss of control. The opposite sense of vortex swirl in that case would increase the total dynamic pressure – and thus the thrust – by a factor of four.
Using the same vortex parameters as in the sections before the following results for the BoMR are shown only, which already indicates that a normal vortex orientation appears much less critical than longitudinal or lateral vortex orientations. The vortex is placed along the y axis lateral across the center of the rotor disk and its swirl is in the same sense as the rotor rotation as indicated in in Fig. 2(c). When the vortex is located at the hub center, it therefore reduces the dynamic pressure everywhere, requiring additional collective control to retrim the thrust, and some longitudinal control to remove the lateral asymmetry in lift. Results are given in Fig. 14. As seen by the scales the impact of the orthogonal vortex is much less when compared to the longitudinal or lateral vortex orientation. Power and thrust variations are less than 5% for a central vortex position, and the rotor control ratios for collective and longitudinal cyclic are less than 0.15, thus leaving large margins for further rotor control. The longitudinal flapping development that occurs when no retrim is performed is so small that it can be ignored. Therefore, an orthogonal vortex-rotor interaction can be considered as not hazardous (even for larger and stronger vortices than considered here), in contrast to the other vortex orientations.

Figure 14. Rotor power, thrust, RCR and RFR variations for an orthogonal vortex. (a) Power and thrust variations. (b) RCR and RFR.
5.0 CONCLUSIONS
This study focuses on the potential impact on safety of small helicopters and ultralight rotorcraft, such as autogyros or coaxial helicopters, flying within strong wind turbine vorticities. As example a 7 MW wind turbine in the most critical operating condition, generating the maximum circulation vortex, is taken. All results found here are based on quasi-steady rotor-vortex interactions. The major results of this investigation are as follows.
The most critical conditions are experienced when the vortex lies within the rotor disk and is oriented in longitudinal (flight) direction.
Retrimming the rotor requires collective and cyclic controls of several degrees magnitude.
Whether these are critical or not depends on the available control margins during flight in undisturbed atmosphere, and these depend both on the operational condition and on the individual rotorcraft hardware.
In high-speed flight usually small margins remain for vortex disturbance mitigation, thus critical conditions can result, especially for small rotors of low-tip speed.
In case of no retrim, some rotor flapping develops. Its magnitude depends on the rotor blade Lock number: The larger it is, the more flapping results.
Depending on the available margin of flapping, which again is a function of the operational condition and rotorcraft construction, the amount of flapping may become dangerous because the blades may hit the fuselage (e.g., helicopter main or tail rotor), or cause mast bumping (in case of teetering rotors), or cause blade collisions (in case of coaxial rotors).
Retrimmed or not, the rotor power undergoes significant variations that may also exceed the available maximum power, and in consequence cause a loss of rotor speed of rotation and/or yawing of the rotorcraft.
Vortex axis orientation orthogonal to the rotor disk cause disturbances that are about one order of magnitude less than longitudinal or lateral vortex axis orientations.
An additional blade tip mass, resulting in a smaller Lock number, would reduce the amount of flapping and thus can alleviate the vortex impact.
Because every rotorcraft is differently designed with different Lock number, different maximum control ranges, different flapping ranges, different control angles required for trim in undisturbed air and different flapping angles obtained during this trim, the available control angle and flapping margins must be evaluated always individually in order to judge the severity of a vortex impact.
In this article, the interaction problem is simplified by considering the wind turbine vortex as “rigid”, i.e. not deforming during the interaction with the rotor. Although this is a reasonable assumption in fast-forward flight, at low speed the rotor downwash will significantly disturb the vortex by downward convection, thus increasing the vortex-rotor separation and with it the vortex-induced velocities. Also, a free-flying helicopter will change its flight path when approaching a vortex that is strong enough to significantly change its rotor thrust and hub moments. This as well tends to increase the rotor-vortex distance, but may cause handling quality issues. Therefore, the rigid vortex assumption leads to over-conservative results in principle.



















