Article contents
A Two-Parameter Method for Calculating the Two-Dimensional Incompressible Laminar Boundary Layer
Published online by Cambridge University Press: 04 July 2016
Summary:
In most one-parameter methods of calculating laminar boundary layers it is assumed that the non-dimensional parameters H=δ1/δ2, I=δ2τW/μu1 and L = 2{I−λ(H+2)}, depend only upon the pressure gradient parameter λ=u1δ22/v. In this paper it is shown theoretically that a more accurate, two-parameter representation is
L=F0(λ)−μG0(λ)
I2=F1(λ)−μG1(λ),
where μ=λ2U1U1/(U1)2. Careful examination of the available range of exact solutions of the boundary layer equations has enabled the four functions F0, G0, F1, G1, to be tabulated, and the above functional forms agree with the exact solutions to a remarkable accuracy.
In view of the fact that a reasonable first approximation to L is usually 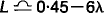 , we write
, we write
 ,
,
and it is then shown that the momentum integral equation becomes
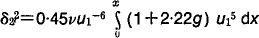
This equation is easily solved by iteration, setting g=0 in the first approximation, and convergence is extremely rapid.
The method is, in effect, a refinement of that due to Thwaites, which is universally accepted as one of the better of the existing calculation methods. Detailed calculations made by the present method indicate that the errors are only 5% of those given by the Thwaites method.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1967
References
- 10
- Cited by


