Periodic morphing of a NACA6409 aerofoil in ground effect, its wake mechanisms and thrust generation

Abstract

The camber morphing of an aerofoil in ground effect was investigated using the FishBAC method and Detached Eddy Simulations with the k-omega SST turbulence model at a Reynolds number of 320,000. The aerofoil was periodically morphed at a start location of 25% chord from the leading edge with a trailing edge deflection range of 0.1% to 3% and morphing frequencies between a Strouhal number of 0.45 to 4 at a constant ground clearance of 10%. Periodically morphing the aerofoil using a sinusoidal function showed that lift and drag increased on the downstroke and decreased on the upstroke in the cycle, resulting in periodic values of lift and drag throughout the cycle. The amplitude of lift and drag increased as the morphing frequency and/or trailing edge deflection increased. It was found that the wake characteristics varied as a function of trailing edge deflection and morphing frequency. For small trailing edge deflections below 0.4% and frequencies below a 2.2 Strouhal number, Kelvin Helmholtz shedding was observed, and above this the wake became chaotic. Large trailing edge deflections showed Von-Karman shedding, where the interaction between the lower counter-clockwise vortex and the ground plane resulted in a jet-like flow that caused forward thrust. For the maximum deflection and morphing frequency tested in this study, reversed Von-Karman shedding was observed, which caused forward thrust from the interaction of the two-shedding counter-rotating vortices. Von-Karman or reversed Von-Karman shedding shows positive thrust generation, however, chaotic shedding should be avoided due to large drag gains. Varying the Reynolds number caused the Strouhal number to change as they depend on the same variables. It was found that the Strouhal number variation had a large effect on the wake, however, the Reynolds number had a minimal effect.

Nomenclature

AoA

=angle-of-attack

c

=chord length

Cd

=drag coefficient

Cl

=lift coefficient

Cp

=pressure coefficient

D

=drag

f

=frequency

GE

=ground effect

h

=height above ground

h/c

=ground clearance to chord ratio

L

=lift

l/d

=aerodynamic efficiency

Sr

=Strouhal number

t

=time

TE

=trailing edge

TKE

=turbulent kinetic energy

u

=velocity

Wte

=trailing edge deflection to chord ratio

x

=distance along aerofoil

Xs

=morphing start location along the chord

Yc

=aerofoil chord

Yt

=aerofoil thickness

$\omega $

=vorticity

1.0 Introduction

Flying a wing in ground effect causes enhanced performance that increases lift and reduces drag, which was first noticed by pilots landing aircraft who noticed a sudden increase in lift as they landed. Analysis of wings in ground effect is split into chord-dominated, where the ground-effect enhancement is analysed in two dimensions, and span-dominated, where the wing-in-ground effect is analysed in three dimensions [1]. Chord dominated considers the gains in lift from the fixed trailing edge pressure defined by the Kutta condition, which increases the pressure under the wing upstream of the trailing edge. Span dominated considers the wing tip vortices which do not fully develop due to the proximity of the ground, reducing the induced drag, and also pushes the vortices outboard, effectively increasing the span.

Many studies have investigated periodic morphing in freestream such as Ref. [2], who periodically morphed the upper surface of a NACA4415 aerofoil. It was found that due to the Kelvin Helmholtz instability; momentum was transferred to the near-wall flow which almost eliminated the recirculation zone on the aerofoil suction surface. Periodic morphing was also applied to the trailing edge in a freestream study by Ref. [3], which increased the lift and reduced the drag of a NACA0012 with 0.1% trailing edge deflection. In a study by Ref. [4] with larger deflections, the stall angle was found to be increased by the use of periodic trailing edge morphing from momentum transfer. Thrust generation can be achieved with a pitching aerofoil, which has been extensively researched in freestream [5–9], but only a few studies have been conducted in ground effect. One of the first analytical studies [10] of an unsteady aerofoil in ground effect was conducted by Ref. [11], where a soft flat plate was studied, inspired by the propulsion of birds and fishes. The ground effect was found to increase the lift and propulsion efficiency compared to freestream.

A study by Ref. [10] investigated the wake dynamics behind an oscillating aerofoil and found that the introduction of a ground plane enhanced thrust generation. Far from the ground boundary, the pitching wing produced a reversed Von-Karman shedding wake, also known as a thrust generation wake, but in ground effect, the shedding vortices formed pairs seen at high Strouhal numbers and low trailing edge deflections. The pair of counter-rotating vortices naturally rotated to a more upright position so that the resulting jet-like flow aligned with the ground plane and hence caused greater forward thrust. It was said that this would allow the craft to fly faster with minimal loss in efficiency. Other studies, including Refs [12] and [13], have also shown vortex shedding and increased propulsive efficiency in ground effect. Overall, periodic morphing can achieve both reduced separation on the suction surface and propulsion.

Fish Bone Active Camber (FishBAC) morphing was introduced by Ref. [14] who defined a morphing structure for an aerofoil that when morphed, the morphing displacement can be defined. The morphing method was bioinspired allowing for large physical deflections of the trailing edge. A physical model was created by Ref. [15] and a schematic of this is shown in Fig. 1 using a servo and belt system to bend a spine with stringers used to keep the shape of the flexible EMC skin.

Figure 1. Fish Bone Active Camber (FishBAC) concept [16].

There have been many studies investigating morphing wings in freestream, as well as studies investigating pitching and plunging aerofoils in ground effect. However, it has been noted to the best of the authors’ knowledge that there has been little work been carried out on morphing aerofoils or wings in ground effect; this study aims to fill this knowledge gap by building on previous work [16], and demonstrate the flow mechanisms behind morphing wings in ground effect. This paper is arranged into sections which outline the methodology, discussion of periodic morphing and conclusions of the study.

2.0 Methodology

This study focuses on the application of periodically morphing wings to a UAV craft, therefore, a Reynolds number of 320,000 was chosen as this is a typical value for UAVs during flight [17]. The Reynolds number was also above the critical value of 100,000, therefore, the flow characteristics are less sensitive to changes in Reynolds number [18]. The NACA6409 aerofoil profile is used in this study due to is popularity for ground effect investigations [19–23] due to its camber providing high aerodynamic performance. Also, the profile is of substantial thickness for strength and to house morphing systems, especially for use on a UAV. A wing in ground effect craft typically has a low angle-of-attack wing due to prone and earlier stall from variations in ground clearance, therefore, an angle-of-attack of 4 degrees was used in this study [16]. The analysis was performed using computational fluid dynamics (CFD) with Star CCM+ commercial CFD software. Star CCM+ is a multidisciplinary multiphysics software platform created in Java by CD Adapco before being sold to Siemens [24]. The aerofoil was investigated using the Detached Eddy Simulation with the k-omega SST turbulence model [25] and the revised k-omega [26] within Star-CCM+. For the aerofoil a domain size was shown in Fig. 2 along with the boundary conditions, the moving ground was defined by applying a tangential velocity vector to the ground wall with the same velocity as the freestream.

Figure 2. Aerofoil domain size and boundary conditions.

The computational domain used the trimmer meshing method shown in Fig. 3 with control volumes to refine the mesh in certain areas. During simulation, the aerofoil was morphed, which deformed the mesh. In this study, the mesh vertices were moved by a defined amount using the built-in morpher within Star CCM+. The mesh quality was analysed throughout the morphing process and remained of high enough quality. Therefore, re-meshing was not required within the trailing edge displacement range tested in this study. The mesh used 10 prism layers to capture the boundary layer with the first cell height set to ensure that a y+ value of 1 was achieved as recommended in the user manual for the k-omega SST turbulence model [27]. The prism layer reduction method built into Star CCM+ was used at the trailing edge of the aerofoil.

Figure 3. Mesh around NACA6409 aerofoil.

The aerofoil was morphed periodically over time using the FishBAC morphing method described in the introduction. The FishBAC method works by adding a defined displacement to the aerofoil camber line. Therefore, in CFD simulations such as this study, the mesh vertices can be defined to move the displacement defined by the FishBAC equation to morph the aerofoil. The displacement of the trailing edge per time step $\left( y \right)$ was defined by Equation (2), which consists of the FishBAC equation and the sinusoidal time-dependent term. The FishBAC term defines the morphing profile of the camber line with a morphing start location of ${x_s}$ at any position along the chord with a maximum trailing edge deflection of ${w_{te}}$ shown by the schematic in Fig. 4. The maximum displacement ${w_{te}}$ values in this study ranged from 0.1c to 3c.

Figure 4. Schematic of FishBAC morphing method applied to NACA6409.

The sinusoidal term in Equation (2) is the time-dependent term which periodically varies the trailing edge deflection. The motion of deflection was carried out using a sinusoidal function where $f$ defines the morphing frequency carried out over time $t$ . The morphing frequency presented in this study is presented in terms of the non-dimensional frequency (Equation (1)) and range between a Strouhal number of 0.45 and 4.

(1) \begin{align}Sr = \frac{{fc}}{u}\end{align}

The start location of morphing was set to ${x_s}$ =0.25 $c$ , as initial studies showed the upper surface separation occurred quite early along the upper surface.

(2) \begin{align}{y_{ts}} = \frac{{{w_{te}}{{\left( {x - {x_s}} \right)}^3}}}{{{{\left( {1 - {x_s}} \right)}^3}}}{\rm{sin}}\left( {2\pi ft} \right)\end{align}

Morphing was performed from a fully converged DES solution that had run for 0.1 s to ensure a steady settled flow. After 0.1 s the morphing was turned on and the simulation was run up to 0.4 s, the lift and drag values were time-averaged between 0.2 and 0.4 s to ensure that the flow had settled after the morphing had started. This resulted in the lift and drag being time-averaged over 25 cycles for a Strouhal number of 0.45 and 225 cycles for a Strouhal number of 4, where the Strouhal number corresponds to the morphing frequency. Using the formulation of Ref. [28], the resultant variance was determined to be 2.6x10⁻⁵ for the lift and 2.2 × 10⁻⁷ for the drag and no significant changes in variance were seen for an increased sample size of 24 at a Strouhal number of 3.5.

3.0 Mesh independence and validation

A mesh independence study was first carried out to ensure that the grid spacing was sufficient to capture the flow details whilst not being overly refined, which would increase the computational cost. This mesh independence study was carried out using the outlined ASME V & V 20 Committee [29] method to determine the discretisation error. Three mesh refinements were carried out (fine, medium and coarse) as shown in Table 1 for a NACA6409 aerofoil at 4 degrees angle-of-attack.

Table 1. DES mesh cell count with corresponding lift and drag values

Using the two finest grids, the Richardson extrapolation can be used to determine the value of lift and drag for zero-grid spacing. This was done using Equation (3), where ${p_r}$ is the zero-grid spacing, with the lift and drag coefficients are denoted by $f$ and the subscript denotes fine, medium, and coarse meshes. The value $p$ is the order of convergence which is determined by $p = \ln \left[ {\left( {{f_c} - {f_m}} \right)/\left( {f - {f_f}} \right)} \right]/\ln \left( r \right)$ , where $r$ is the refinement ratio equal to 2 [29].

(3) \begin{align}{p_r} = \;{f_f} + \left( {{f_f} - {f_c}} \right)/\left( {{r^p} - 1} \right)\end{align}

The zero-grid spacing value for the lift was determined to be Cl = 1.0598 and for the drag, the zero spacing was determined to be Cd = 0.0167. Further checks are required to determine if the zero-grid spacing formed an asymptote from the three-grid spacings. This was carried out using the grid convergence index (GCI) defined by Equation (4). The factor of safety $\left( {{F_s}} \right)$ was set to 1.25 for comparisons over three grids [29]. The relative error $\left( \varepsilon \right)$ was determined using pairs of mesh refinements, $\varepsilon = \;\left( {{f_f} - \;{f_m}} \right)/{f_f}$ for the fine mesh and $\left( {{f_m} - \;{f_c}} \right)/{f_m}$ for the coarse. This yielded a value of CGI = 0.02% for the lift with the fine mesh and 0.263% for the coarse mesh. For the drag, a value of GCI = 0.0298% was determined for the fine mesh and GCI = 0.263% for the coarse mesh.

(4) \begin{align}GCI = \;\frac{{{F_s}\left| \varepsilon \right|}}{{\left( {{r^p} - 1} \right)}}\end{align}

Having determined the GCI, the solution was then checked to see it fell within the asymptotic range of convergence where the solution is approximately equal to 1 when checking the values using Equation (5). A value of 0.998 was obtained for lift and 0.999 for drag. The values are close to 1, which satisfies Equation (5) and thus shows the convergence for the zero-grid spacing.

(5) \begin{align}1 = \;\frac{{GC{I_{fm}}}}{{\left( {{r^p}GC{I_{mc}}} \right)}}\end{align}

Table 2. Mesh size error

Figure 5. NACA0012 pitching aerofoil lift freestream.

After checking the zero-grid spacing convergence, the values of the lift and drag shown in Table 1 were compared with the zero-grid spacing values of lift and drag shown in Table 2. It was seen that the fine mesh had converged to a very high level, while the medium mesh showed a slightly higher error. The coarse mesh was discarded due to the large error, especially for the drag. The medium mesh was carried forward as it was accepted that the error was of acceptable level and further refinement would significantly increase the computational cost.

After performing a mesh independence study for the NACA6409 aerofoil, a validation study was then performed to validate the mesh design and physics setup. A common validation case for morphing and pitching aerofoils is a study by Ref. [30] using a NACA0012 profile pitched about its quarter chord. The pitch angle of the aerofoil throughout its pitch cycle was defined over time t using the equation ${\alpha _t} = {\alpha _m} + \Delta \alpha \sin \left( {\omega t} \right)$ where the initial starting angle-of-attack ${\alpha _m} = 10^\circ $ and the amplitude $\Delta \alpha = 15^\circ $ . The reduced frequency $k = \frac{{\omega c}}{{2{U_\infty }}}$ showed the aerofoil pitching frequency, where the pitching frequency was defined as $\omega = 2\pi {f_o}$ and ${f_o}$ the frequency in Hz. A comparison was made against the reduced frequency of $k = 0.1$ . The CFD with the medium mesh was applied to the pitching aerofoil using the NACA0012 aerofoil and the lift shown in Fig. 5. Comparing the CFD of this study to the experimental data showed a strong correlation with the CFD showing a maximum lift at 22 degrees compared to the experiment where the maximum lift was seen at 25 degrees angle-of-attack. This was due to the flow stalling earlier in the CFD; and this was also observed by Ref. [3]. After the stall, the flow reattached almost instantly, causing the lift to form a second peak before the lift decreased on the down stroke. Both the experiment and CFD showed a hysteresis loop with lower lift values on the downward stroke. As the pitching motion slowed down towards -5 degrees, due to the sinusoidal motion, the flow had time to recover and attach to the upper surface, resulting in a slightly higher lift on the upstroke. As this study did not focus on highly separated flows, the small discrepancy in stall angles of 22 degrees and 25 degrees was not considered significant. Due to the close comparison between both the experimental data [30] and the CFD carried out by Ref. [3], the CFD was validated in this study.

4.0 Results and discussion

4.1 Periodic morphing analysis

Periodic morphing was applied to the NACA6409 aerofoil using the FishBAC morphing method with a ground clearance of 10% of the chord with the camber morphing starting at 25% of the chord from the leading edge using DES simulations. The simulations were initially carried out up to 0.1 s until a converged solution was reached then the morphing began at 0.1 s up to 0.4 s. The lift and drag were then time-averaged between 0.2 and 0.4 s (as shown by Cl and Cd in Fig. 6) and due to the sinusoidal motion, both the lift and drag had a fluctuation around the time-averaged lift and drag. It was observed that the aerofoil characteristics were similar throughout the range of morphing frequencies and trailing edge deflections tested and that the only factor that changed was the wake dynamics. Therefore, an overview of the morphing aerofoil is presented here in this section before analysing the wake characteristics.

Figure 6. Lift and drag of morphing at 0.9 Strouhal number and 0.125% trailing edge deflection.

Figure 7. Periodic morphing lift for 4degree AoA, xs = 25%, 10% ground clearance.

Figure 8. Periodic morphing drag for 4degree AoA, xs = 25%, 10% ground clearance.

As the aerofoil was periodically morphed, the lift and drag values would fluctuate in time. This yields the mean lift $\left( {{C_l}} \right)$ and drag $\left( {{C_d}} \right)$ values as well as the fluctuating values of lift $\left( {c'_{\!\!l}} \right)$ and drag $\left( {c'_{\!\!d}} \right)$ about the mean shown in Fig. 6 for a morphing frequency of 0.9 Strouhal number and trailing edge deflection of 0.1% chord. Figure 6 also shows the initial period of no morphing to obtain a steady solution from 0 to 0.1 s, the period from 0.1 to 0.4 s where morphing was applied and the period between 0.2 and 0.4 s where the lift and drag were time-averaged.

For the range of morphing frequencies and trailing edge deflections tested, the time-averaged lift (Fig. 7) and time-averaged drag (Fig. 8) contour plots were analysed. Both plots show a delta of how much the lift and drag varied compared to the non-morphing aerofoil under the same conditions and profile. It was seen that by increasing both the trailing edge deflection and the morphing frequency the lift increased, and the drag reduced. The lift and drag varried at different rates as the moprhing frequecy and trailing edge deflection was varied. Large moprhing deflections and frequencies showed a rapid decrease in drag and linear increase in lift. This resulted in a peak aerodynamic efficiency to occur at a trailing edge deflection of 2% and a morphing frequency of 2.69 Strouhal number. At either low morphing frequencies, low trailing edge deflections or both low frequencies and trailing edge deflections, lift was found to have reduced compared to the baseline non-morphing aerofoil. For the drag however, there was a decrease in drag at the same conditions where lift decreased, large reductions in drag were seen when both the morphing frequency and trailing edge deflection were increased together which resulted in thrust generation as shown by the negative drag value in Fig. 8.

As can be seen in Fig. 8 there were large negative drag values which are indicative of thrust generation wakes. The thrust coefficient $\left( {{C_T}} \right)$ was analysed for the range of morphing frequencies and trailing edge deflections using Equation (6). The thrust was represented by ${F_T}$ in Newtons, the air density by $\rho $ , the pitching frequency $f$ and the chord $c$ .

(6) \begin{align}{C_T} = \frac{{{F_T}}}{{\rho {f^2}{c^4}}}\end{align}

The amount of thrust produced was analysed and the thrust coefficient is shown in Fig. 9 for the range of morphing frequencies and trailing edge deflections tested in this study. It was observed that at low trailing edge deflections and morphing frequencies that negative thrust was produced, however, at low trailing edge deflections and morphing frequencies momentum transfer occurs which improve the aerodynamic efficiency.

Figure 9. Thrust coefficient of periodic morphing aerofoil at 4 degrees AoA and 10% ground clearance.

The pressure was shown in Fig. 10 for a complete morphing cycle with a morphing frequency of 2.69 Strouhal number and a trailing edge deflection of 2% of the chord. It was seen that as the aerofoil was morphed downwards, the camber increased, and the pressure increased on the aerofoil’s lower surface with the largest pressure being at maximum deflection. From the quarter chord location on the upper surface to the trailing edge, it was seen that there was a slight increase in suction on the lower surface. This showed that most of the lift gains were from the lower surface in-ground effect. The pressure on the lower surface increased due to the increase of aerofoil camber and also the trailing edge becoming closer to the ground which further increases the ground effect enhancement, causing gains in lower surface pressure. Morphing the aerofoil upwards caused the trailing edge to be further away from the ground, which reduced the ground effect enhancement and thus reduced the lower surface pressure along with a reduction in the aerofoil camber. The reduced aerofoil camber at large deflections caused the pressure magnitude to flip between the lower and upper surface similar to that of an inverted wing in ground effect. It was seen at -1% deflection on the upwards cycle that at approximately 65% location along the chord the lower surface pressure became negative, and the upper surface pressure became positive. At -2% trailing edge deflection, the suction on the lower surface began at 0.3c, showing that the amount of suction along the chord increased as the aerofoil was morphed upwards. The magnitude of suction on the lower surface and positive pressure on the upper surface resulted in an overall negative lift for maximum upward deflection at -2% trailing edge deflection. Similar observations were made for the pressure coefficient around the aerofoil for the range of morphing frequencies and trailing edge deflections tested. At low morphing frequencies and trailing edge deflections, it was observed that the variations in pressure throughout the cycle were smaller and therefore no suction occurred on the upper surface and no negative lift throughout the morphing cycle. At higher morphing deflections or morphing frequencies, it was observed that the suction on the upward cycle and the pressure on the downward cycle for the lower surface increased compared to lower morphing deflections and frequencies.

Figure 10. Pressure coefficient for one complete cycle at 2.69 Strouhal number morphing frequency and 2% trailing edge deflection.

Looking at the lift and drag over one complete cycle showed a hysteresis loop throughout the range of morphing frequencies and trailing edge deflections tested, where both lift and drag were different between the up and down strokes of the cycle. At low trailing edge deflections, it was observed that there was minimal variation in lift and drag between the up and down strokes. Figure 11 shows the lift and drag for a morphing frequency of Sr = 2.69 and 4 and a trailing edge displacement of, ${w_{te}}$ = 2% and 3%. It was seen that the biggest hysteresis loop was from Fig. 11 increasing the morphing frequency as shown in where the frequency was increased from 2.69 to 4. The difference in lift and drag on the up and down stroke was much less for varying the trailing edge deflection compared to varying the morphing frequency (shown in Fig. 11) by varying the trailing edge deflection from 2% to 3%. The hysteresis loop was also seen by Ref. [4] who periodically morphed an aerofoil in freestream to delay stall. It was observed that the direction of the hysteresis loop was clockwise and was the result of different levels of separation between the up and downstroke of the cycle. During the down stroke, the flow at the trailing edge is pulled downwards and comes to an abrupt stop as the trailing edge deflection downwards deflection stops due to the solid aerofoil surface. On the upward stroke, however, the flow is pushed upwards and as the aerofoil comes to a stop, the upward momentum of the flow causes the flow to carry on upwards. The greater the morphing frequency and trailing edge deflection, the greater the momentum induced into the flow. The flow also struggles to reattach on the upwards deflection, therefore, causing a hysteresis loop that is dependent on the trailing edge deflection and morphing frequency.

Figure 11. Hysteresis loop lift and drag of the periodic morphing wing.

4.2 Wake analysis

In literature, Ref. [31], it was mentioned that the wake has a large impact on the performance of the aerofoil and determines the overall performance. In this section, the wake is analysed to identify key patterns and how these patterns correspond to the changes in lift and drag that were seen in Figs. 7 and 8.

In Fig. 12, at low trailing edge deflections and morphing frequencies, a Kelvin Helmholtz instability was seen to occur. This type of shedding was caused by the two shear layers leaving the trailing edge being forced to slide over each other and due to the periodic morphing, the amount of shear between these two layers varied. This caused an instability where the wake was observed to have a wave-like flow behind the aerofoil, as shown in Fig. 12, which was also seen by Ref. [31] who investigated periodic morphing aerofoils in freestream. For a trailing edge deflection of 0.125% and a morphing frequency of 0.9 Strouhal number, it was found that there was a small increase in aerodynamic efficiency of 5.4%. This was due to the Kelvin Helmholtz instability, which caused a transfer of momentum from the freestream to the shear layer, reducing the separation on the upper surface. This reduced the drag but as aerofoils always produce maximum lift with some separation, the reduced separation from the periodic morphing caused a reduction in lift.

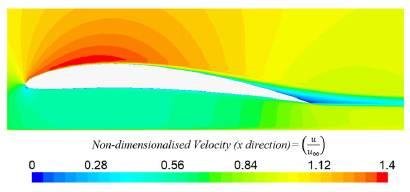
Figure 12. Non-dimensionalised Velocity (with freestream) in x direction for Strouhal number of 3.58 and 1% trailing edge deflection.

Increasing the camber of the aerofoil caused the pressure gradient along the upper surface to decrease and with high deflections, this becomes an adverse pressure gradient and the flow separates. As the aerofoil was about to separate, the Kelvin Helmholtz instability no longer occurred, this caused an unsteady chaotic wake which was shown in Fig. 13 by looking at the wake vorticity. It was found that at a morphing frequency of 2.69 Strouhal number and 0.6% trailing edge deflection that the chaotic wake was observed.

Figure 13. Periodic morphing at a Strouhal number of 2.69 and deflection of 0.6% chord.

Further increases in the trailing edge deflection as morphing frequency caused Von-Karman shedding to occur, as shown in Fig. 15. This showed that the chaotic wake was a transitional phenomenon between the Kelvin Helmholtz instability and the Von-Karman shedding. Unlike the Kelvin Helmholtz where drag was reduced through reduced amounts of upper surface separation, the Von-Karman shedding produced thrust which reduced the overall drag.

In this study, Von-Karman shedding was observed to produce thrust, this shedding is usually associated with increased drag in freestream, however, the proximity of the ground has additional effects. The interaction between the two counter-rotating vortices for Von-Karman shedding has an upstream resultant vector that increases the drag in both the freestream and ground effect, increasing drag. However, in the ground effect, there is an additional resultant force vector caused by the interaction between the shedding vortices and the ground. If this resultant vector between the vortices and ground is bigger than the resultant upstream vector, then Von-Karman shedding produces forward thrust when in ground effect. The ground plane was simulated with a tangential velocity vector that interacted with the Von-Karman shedding caused by periodic morphing. The direction of rotation of the shedding vortex closest to the ground showed a jet-like flow formed between the moving ground plane and the rotating vortex analogous to a car wheel pushing the aerofoil in the forward direction. A schematic of the Von-Karman Shedding vortex is shown in Fig. 14.

Figure 14. Schematic of interaction between Von-Karman vortex shedding and ground.

Figure 15. Non-dimensionalised Velocity (with freestream) in x direction for Strouhal number of 3.58 and 1% trailing edge deflection.

This was visualised by looking at the velocity of the Von-Karman shedding of the 3.58 Strouhal number morphing frequency and 1% trailing edge deflection shown in Fig. 15. As the shedding vortex travels downstream, it was seen that the velocity near the ground was much higher than in the freestream. The vortex shedding showed two counter-rotating vortices with a distance of approximately 0.1 chord length between the centre of the two rotating vortices.

For the highest morphing frequency tested in this study with the highest trailing edge deflection, it was seen that reversed Von-Karman shedding occurred. This can be referred to as a thrust generation wake due to the interaction between the two counter-rotating vortices causing a velocity vector in the downstream direction. It was seen that the drag became negative due to the thrust generated. As demonstrated by the schematic in Fig. 16 there was still interaction between the vortices and the ground. Due to the rotation direction of the vortices, the interaction between the vortex closest to the ground and the moving ground plane caused a resultant upstream jet-like flow, which created an upstream thrust that increased drag. For the reversed Von-Karman case it was found that the interaction between the two counter-rotating vortices was stronger than the interaction between the vortex and ground which caused overall forward thrust. Unlike the Von-Karman shedding, the reversed Von-Karman had a stronger resultant jet from the interaction of the vortices compared to the interaction of the vortices and ground. Looking at the vorticity it was seen (Fig. 17) for a Strouhal number of 3.58 and 1% trailing edge deflection, the wake showed clear Von-Karman shedding with equal spacing of approximately 0.1c from centre to centre of the counter-rotating vortices.

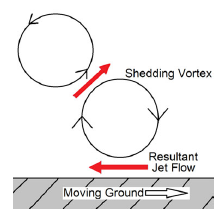
Figure 16. Schematic of interaction between reversed Von-Karman vortex shedding and ground.

Figure 17. Vorticity plot of periodic morphing Strouhal number 3.58 and deflection of 1%.

It was observed that at higher morphing frequencies and trailing edge deflections, the spacing of these two vortices became much closer as shown in Fig. 18, due to the vortex closer to the ground moving at a slower rate downstream from opposing the motion of the ground. The vortex furthest from the ground was less affected by the opposite direction of the ground motion and therefore initially travelled downstream faster, causing the vortex pair to become more upright. Once the vortices are close together, they travel downstream at the same speed. Similar observations were made by Ref. [10] for a pitching aerofoil in ground effect.

Figure 18. Vorticity plot of periodic morphing Strouhal number 4 and deflection of 3% (left) and schematic (right).

The Von-Karman and Reversed Von-Karman wakes observed in this study are similar to those in the freestream, which have also been observed in literature by Refs [6] and [32], where the interaction between pairs of counter-rotating vortices caused a jet-like flow. A schematic is shown in Fig. 19, where the resultant thrust vector is represented by the arrows, it is also important to note that these are not aligned with the flow, so the resultant forces will have a thrust and lift component. The jet-like flow was observed in a study by Ref. [10] where this was visualised using particle image velocimetry.

Figure 19. Von-Karman shedding (top) and reversed von-Karman shedding (lower).

Figure 20 summarises the different wakes obersed in this study. At low morphing frequencies and small trailing edge deflections, the Kelvin-Helmholtz instability was observed. As the trailing edge deflection increased there was a small transition where the wake began to separate and shed, however, due to the flow being on the verge of separating, reattachment occurred before separating again, resulting in a chaotic flow. Further increasing the trailing edge morphing caused Von-Karman shedding and even further increases caused reversed Von-Karman shedding.

Figure 20. Wake characteristics as a result of periodic morphing at different frequencies and deflections.

It was seen in this section that different wake characteristics occur for different morphing frequencies and trailing edge deflections. From the observation of the wake for the range of morphing frequencies and trailing edge deflections, the type of shedding behind the aerofoil was plotted in Fig. 21. This is an important plot as it shows the region of morphing frequencies and trailing edge deflections to be avoided.

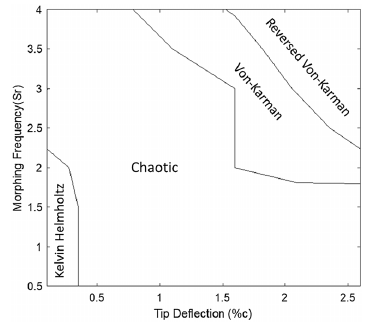
Figure 21. Wake characteristic map for periodic morphing in 10% ground effect.

The fluctuations of lift (Fig. 22) and drag (Fig. 23) both showed very similar trends. Lift and drag would naturally fluctuate throughout the morphing cycle due to increasing and decreasing camber. For small trailing edge deflections and morphing frequencies, it was seen that the fluctuation in lift and drag was approximately the same value as the baseline lift and drag. This results in zero or small values of negative lift and drag at maximum upward deflection of the aerofoil and almost double the lift and drag at maximum downward deflection. For large trailing edge deflections and morphing frequencies, it was found that both the lift and drag fluctuations were an order of magnitude of approximately 10 times higher than the mean lift and drag resulting in significant negative and positive lift and drag variations throughout the morphing cycle.

Figure 22. Periodic morphing lift fluctuation for 4degree AoA, xs = 25%, 10% ground clearance.

Figure 23. Periodic morphing drag fluctuation for 4degree AoA, xs = 25%, 10% ground clearance.

The main interest in this study was the mean lift and drag, however, it was discussed and shown in Figs. 22 and 23 that both the lift and drag had large fluctuations as the wing was periodically morphed. Some conclusions can be drawn from these fluctuations based on the observations made from the wake analysis. The variation in camber during a morphing cycle will vary the lift and drag, however, the magnitude of the fluctuations is much greater than would be expected from the camber variation alone. It was observed that the largest variations in lift and drag are for the thrust-generating regimes, also increasing the morphing frequency and tip deflection caused the fluctuations to increase dramatically as the regimes entered the Von-Karman and Reversed Von-Karman wakes.

At lower morphing frequencies and trailing edge deflections, the variations in lift and drag can be attributed to variations in camber and small flow separations on the upper surface of the aerofoil. Increasing the morphing frequency results in a faster shedding frequency, which is attributed to larger fluctuations in drag. This is because the thrust generated is not a constant force, but has a peak force at maximum deflection positions.

It was observed that the thrust vector from the shedding vortices is not directly aligned parallel with the ground seen in Fig. 19. Therefore, there will be a horizontal and vertical component from the resulting wake shedding, the horizontal being associated with the thrust generation as previously discussed. The vertical component causes the lift component to fluctuate, increasing the morphing frequency and the trailing edge deflection causes the vortex pairs to have a stronger resultant force. It is also observed that there is a stronger interaction between the vortices in the vertical direction, causing the vortex pairs to move upwards. Finally, by looking at the pressure plot (Fig. 10), there are large increases in pressure under the wing throughout the morphing cycle, increasing both the lift and drag fluctuations. Therefore, from the wake analysis, and looking at the wing pressures, several factors are causing the large fluctuations in lift and drag seen in Figs. 22 and 23.

Figure 24. Varying Reynolds number with variable Strouhal number.

Figure 25. Varying Reynolds number with constant Strouhal number.

4.3 Reynolds number effects

A Reynolds number of 320,000 has been used throughout this study so far, as this is in the range used for UAVs and the intended future application of applying this technology to a ground effect UAV. However, depending on the application, the Reynolds number can vary significantly depending on the flying speed and aerofoil size. Initial analysis has been carried out to vary the Reynolds number, however, this has proved to be a complex area of research. This is due to the fact that varying either the airspeed or chord length to vary the Reynolds number seen in Equation (7) will also vary the Strouhal number at the same time, as this is also dependent on the freestream velocity and chord length, as seen in Equation (1). It was found in this study that the flow is highly dependent on the Strouhal number, so the variation of the Reynolds number poses the problem of varying the morphing frequency to keep the Strouhal number constant or allowing the Strouhal number to vary with the variation of the Reynolds number.

(7) \begin{align}{R_e} = \frac{{\rho uL}}{\mu }\end{align}

Two cases were tested, one where the morphing frequency was fixed, resulting in a variation in the Strouhal number, and the other where the morphing frequency was adjusted to keep it constant. First, the morphing frequency $f$ was fixed at 800 Hz which corresponded to Strouhal numbers of 6, 4.28, 3.08 and 1.64 respectively when the Reynolds number was varied. Four Reynolds numbers (191,500, 268,000, 373,400 and 70,000) were tested for the morphing aerofoil at 10% ground clearance and 2% trailing edge deflection. Figure 24 shows the vorticity of the periodically morphing aerofoil for different Reynolds and Strouhal numbers. For Re = 191,500 and Sr = 6, there is a pair of strong counter-rotating vortices, which are almost upright and show reversed Von-Karman shedding. At Re = 268,000 and Sr = 4.28, the counter-rotating vortex pair became slightly weaker, and the vortex pair was no longer upright with the vortex pair leaning upstream. The vortex pair continued to decrease/reduce in strength and the angle between the vortex pair and the ground decreased even further, reducing the forward thrust. At higher Reynolds numbers, it was seen that the flow became chaotic behind the aerofoil for the case Re = 70,000 and Sr = 1.64, however, there was slightly more vorticity for the chaotic wake.

Secondly, the Strouhal number was fixed at 3.58 and the morphing frequencies of 478, 669 and 907Hz were tested for the Reynolds numbers 191,500, 268,000 and 373,400, respectively. Unlike the fixed frequency case, the 70,000 Reynolds number was not tested for the fixed Strouhal number case as the morphing frequency required to maintain a constant Strouhal number was outside of the validation range. For a constant Strouhal number of 3.58, as the Reynolds number is increased (Fig. 25), it can be seen when increasing the Reynolds number that there is little variation in the wake behind the aerofoil compared to when the Strouhal number was not fixed. This is an important finding as it can be concluded that the Strouhal number is the factor causing the variation in wake characteristics and not the Reynolds number. The main difference between the three Reynolds numbers shown in Fig. 25 is that the upright angle of the vortex pair reduces slightly and there is a slight increase in vorticity as the Reynolds number increases.

5.0 Conclusion

In this study the periodic morphing of a NACA6409 aerofoil in ground effect with 10% clearance was investigated using the FishBAC morphing method. Detached Eddy Simulation with a k-omega SST turbulence model was used with a Reynolds number of 320,000 as this study aimed to apply the technology to UAV craft. It was found in this study that morphing at different trailing edge deflections and frequencies produced different wake-shedding patterns. Morphing frequencies were analysed between a Strouhal number of (0.45 to 4.02) and trailing edge deflections between 0.05% and 3% of the chord length. It was found that as the aerofoil was periodically morphed, the pressure increased on the lower surface and decreased on the upper surface for the downstroke, while on the upstroke the lower surface pressure decreased and the upper surface increased. As the morphing frequency and trailing edge deflection increased, the amount of pressure change between the upper and lower surfaces increased. This resulted in the negative lift being produced for mid to high morphing frequencies and trailing edge deflections on the upward stroke.

At lower morphing frequencies and trailing edge deflections, Kelvin Helmholtz shedding occurs. In some cases, the Kelvin Helmholtz increased the aerodynamic efficiency due to momentum transfer from the freestream to the boundary layer causing a reduction in drag, but also reduced the lift. Increasing the morphing frequency and trailing edge deflection caused the Kelvin Helmholtz to turn into a chaotic shedding structure which decreased the aerodynamic efficiency. Increasing the morphing further caused Von-Karman shedding, and at the highest trailing edge deflection and morphing frequencies, Von-Karman shedding was reversed. From the literature, it was found in freestream that the interaction between the counter-rotating vortices of reversed Von-Karman shedding caused a jet-like flow which was also seen in this study. The direction of this flow was upstream for the Von-Karman, effectively increasing the drag, and a downstream direction for the reversed Von-Karman, known as a thrust-generating wake. In this study investigating wings in ground effect, the direction of the rotation of the Von-Karman vortices also caused a jet-like flow in the upstream direction, comparable to freestream. However, in the ground effect, the interaction of the vortex closest to the ground and the moving ground plane caused the aerofoil to be pushed forward for Von-Karman shedding. In the ground effect, the reversed Von-Karman showed a negative interaction (increase in drag) between the vortex and the ground, however, the direction of the jet flow from the interaction of the two vortices was downstream causing forward thrust. It was found that there are high levels of thrust from a periodically morphing wing at high trailing edge deflections and morphing frequencies, therefore there is potential to reduce or downsize the requirements of aircraft propulsion systems, which would require further investigation.

Finally, the Reynolds number was varied in this study, it was found that varying the Reynolds number had a knock-on effect on varying the Strouhal number, as both of these non-dimensional numbers depend on the freestream velocity and chord length. As the Strouhal number was dependent on the morphing frequency $f$ , the Reynolds number could be varied independently of the Strouhal number while simultaneously adjusting the morphing frequency $f$ accordingly. The Reynolds number was also varied with a fixed morphing frequency $f$ . A comparison of the two showed that the Reynolds number had a minimal effect on the wake shedding, whereas the Strouhal number had a large effect on the wake shedding. Further investigation is needed to vary the Reynolds number for different cases or morphing frequency and trailing edge displacements, and to investigate their effect on lift, drag and thrust generation.