Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-08T13:26:04.254Z Has data issue: false hasContentIssue false
  • English
  • Français

Part III. Local Buckling of Monocoque Structures

Published online by Cambridge University Press:  28 July 2016

Get access Rights & Permissions [Opens in a new window]

Extract

In case of normal monocoque aeroplane fuselages relatively strong rings are spaced at distances equal to 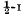diameter of the fuselage, failure of the structure always occurs by instability of the most stressed stringer. The buckling stress, however, is mostly very low, especially, when the number of stringers is great and consequently the cross section of one stringer is small. The value of the stress at failure may be raised by spacing the rings nearer and reducing thereby the free length and, consequently, the slenderness ratio of the stringers. In this case the rings should be constructed of lighter sections in order to balance the increment of weight of the whole structure due to the greater number of rings.

By decreasing gradually the interval between rings a critical distance is reached when the most stressed stringer does not buckle between adjacent rings, but forces one or more supporting rings to deform simultaneously. This form of instability will in the following be termed local buckling of the monocoque structure.

Type
Instability of Monocoque Structures in Pure Bending
Information
The Aeronautical Journal , Volume 42 , Issue 328 , April 1938 , pp. 319 - 333
Copyright
Copyright © Royal Aeronautical Society 1938

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

35 V. Ref. 7.

36 The minimum condition of the function

P or=F(x)=A(x)/B(x)

is given by

dF(x)/dx=[dA(x)/dx]/B(x)–[dB(x)/dx][A(x)/B 2(x)]=0

or

[dA(x)/dx]–[A(x)/B(x)][dB(x)/dx]=0.

This equation may be transformed into

P or=[dA(x)/dx]/[dB(x)/dx].

37 Cf. §3 of Ref. 8.