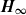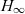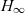Gust load alleviation for flexible aircraft using discrete-time ${\textbf{\textit{H}}}_{\boldsymbol{\infty}}$ preview control

Abstract

Turbulence and gusts cause variations in the aerodynamic forces and moments applied to the structure of aircraft, resulting in passenger discomfort and dynamic loads on the structure that it must be designed to support. By designing Gust Load Alleviation (GLA) systems, two objectives can be achieved: first, realizing higher passenger comfort; and second, reducing the dynamic structural loads, which allows the design of lighter structures. In this paper, a methodology for designing combined feedback/feedforward GLA systems is proposed. The methodology relies on the availability of a wind profile ahead of the aircraft measured by a Doppler LIDAR sensor, and is based on $H_{\infty}$-optimal control techniques and a discrete-time preview-control problem formulation. Moreover, to allow design trade-offs between those two objectives (to achieve design flexibility) as well as to allow specification of robustness criteria, a variant of the problem using multi-channel $H_{\infty}$-optimal control techniques is introduced. The methodology developed in this paper is intended to be applied to large aircraft, e.g. transport aircraft or business jets. The simulation results show the effectiveness of the proposed design methodology in accounting for the measured wind profile to achieve the two mentioned objectives, while ensuring both design flexibility and controller robustness and optimality.

NOMENCLATURE

Flight mechanics

CG

centre of gravity of the aircraft

g

gravitational acceleration ($\mathrm{m/s}^2$)

$I_{\cdot \cdot}$

aircraft moments and products of inertia with respect to body axis system ($\cdot = $ x, y or z) ($\mathrm{kg\,m}^2$)

$L, M, N$

components of the resultant moment about the CG in the body axis system (N m)

m

aircraft mass (kg)

$p, q, r$

components of the aircraft angular velocity vector in the body axis system (rad/s)

$u_K, v_K, w_K$

components of the flight-path velocity vector relative to the Earth in the body axis system (m/s)

$V_{\rm T\!AS}$

true airspeed (m/s)

$w_{\rm gust}$

vertical wind component from the gust (m/s)

$X, Y, Z$

components of the resultant force vector in the body axis system (N)

xyz

body axis system (fixed to the aircraft, with the CG as origin)

$x, y, z$

components of the inertial position vector (inertial displacements) (m)

$\alpha$

angle-of-attack (°)

$\delta_{e,{\rm cmd}}, \delta_{a,{\rm cmd}}^{\rm sym}$

commanded elevator and symmetric aileron deflections, respectively (°)

$\delta_{e,{\rm act}}, \delta_{a,{\rm act}}^{\rm sym}$

elevator and symmetric aileron deflections (output of the corresponding flight control actuator), respectively (°)

$\Phi, \Theta, \Psi$

Euler angles (bank, inclination and azimuth angles, respectively) (°)

Structural dynamics

BR1, BR4

bending moments at stations WR1 and WR4, respectively (N m)

$d_E$

total elastic deformation

$m_i, Q_i$

generalised mass (kg) and force (N) associated with the ith flexible mode, respectively

$n_z^{\rm HTR}$

normal load factor at station HTR

$n_z^{\rm pilot}$

normal load factor at pilot location

$\zeta_i, \omega_i$

modal damping (–) and natural frequency (rad/s), respectively

$\eta_i, \phi_i$

generalised coordinate and mode shape (eigenfunction), respectively

Control

$a_z^{\rm IMU}$

vertical acceleration measurements from the IMU ($\mathrm{m/s}^2$)

$\textbf{\textit{d}}, {\textbf{\textit{d}}}_p$

disturbance input and previewed disturbance input available for the control action, respectively

$q^{\rm IMU}$

pitch rate measurements from the IMU (rad/s)

h

preview horizon (continuous time) or preview length (discrete time)

$H_{\infty}, \| \cdot \|_{\infty}$

infinity norm of a system

$T_{zw}$

closed-loop transfer matrix from the exogenous input to the regulated output

${\textbf{\textit{u}}}, {\textbf{\textit{w}}}$

control and exogenous input vectors, respectively

${\textbf{\textit{x}}}$

state vector of the system

${\textbf{\textit{y}}}, {\textbf{\textit{z}}}$

measured and regulated output vectors, respectively

${\textbf{\textit{y}}}_{\textbf{\textit{d}}}$

preview measurements from the LIDAR

$\gamma$

$H_{\infty}$ performance value

$\boldsymbol{\xi}$

augmented state vector

1.0 INTRODUCTION

As per Part 25 of the FAA Airworthiness Standards⁽¹⁾ and CS-25 of the EASA Certification Specifications⁽²⁾, the strength requirements on an aircraft structure are specified in terms of limit loads (the maximum loads to be expected in service) and ultimate loads (the limit loads multiplied by prescribed factors of safety). The structure must be able to support these limit loads without detrimental permanent deformation or damage. The manufacturer must determine (for all critical combinations of parameters on and within the boundaries of the structural design envelope) the applicable structural design loads resulting from likely externally or internally applied pressures, forces or moments that may occur. The limit loads are defined to be equal to these structural design loads. For proof of a structure, compliance with these strength requirements must be demonstrated for each critical loading condition, considering all of these applied loads.

Of particular interest in this paper are the loads resulting from gust and turbulence conditions. Turbulence and gusts cause variations of the aerodynamic forces and moments applied to the structure of aircraft. By designing Gust Load Alleviation (GLA) systems, the dynamic structural loads can be reduced, allowing for the design of lighter structures (assuming that the sizing/critical cases result from the gust and turbulence loads). Furthermore, the ride quality can be enhanced, resulting in improved passenger comfort.

The design of GLA systems dates back 50 years to the Load Alleviation and Mode Stabilization (LAMS) program of the Boeing B-52E⁽³⁾. Over recent decades, many GLA systems have been implemented on numerous aircraft, such as the Lockheed C-5A/L-1011-500, Boeing B-1 and Airbus A320/A330/A340/A380/A350. The GLA systems on these aircraft are mainly based on feedback measurements from inertial sensors⁽⁴⁾. In some other aircraft, e.g. the Northrop Grumman B-2 and Boeing 787, aerodynamic measurements (from air data sensors) are additionally included to estimate the gust component of the aircraft angle-of-attack⁽⁴⁾, allowing for feedforward control. DLR’s research activities in this direction led to the Open-Loop Gust Alleviation (OLGA) system⁽⁵⁾ and the Load Alleviation and Ride Smoothing (LARS) system⁽⁶⁾.

In the case of inertial sensors, the main limiting factors are the finite number of independent actuators (e.g. Direct-Lift Control (DLC) flaps and ailerons), in addition to their bandwidth and authority. In the case of aerodynamic sensors, these limiting factors can be relaxed to some extent as a result of compensating for the gust component of the aircraft angle-of-attack and of having more lead time in the control loop. Hence the performance of the GLA system is expected to be enhanced, but with the additional limitation of the small looking distance between the sensor (normally located at the aircraft’s nose) and the aerodynamic surface (wing). This makes aerodynamic sensors only beneficial in case of low-speed flight⁽⁷⁾.

The numerous successes of active control technologies for GLA systems logically ended up reaching the maximum technology readiness level (TRL) of 9 for some of these systems. Consequently, the orientation of research activities moved from the design of GLA systems based on classical sensors (i.e. inertial or air data sensors) to the investigation of the potential enhancement in performance when using more advanced/futuristic sensors. Previous work in these directions, especially during the AWIATOR project,¹ led to the Gust Computation System (GCS) and Gust Load Alleviation System (GLAS), as well as the consideration of using Doppler LIght Detection And Ranging (LIDAR) sensors to determine the wind profile ahead of the aircraft⁽⁷⁾. This was based on the observation that, with greater anticipation of near-future loads, higher GLA performance could be achieved.

If the future reference or disturbance inputs to a system are unknown and unpredictable, then the control action is determined by operating upon the instantaneous error, error rate, etc. Such feedback control may or may not achieve the desired performance in tracking the reference input and/or rejecting disturbances. However, it is expected that the performance can be further enhanced if future information about the reference or disturbance inputs becomes available⁽⁸⁾. In the literature, if the control system has some future information about reference or disturbance inputs, then the problem is called preview control (see Ref. [9] for a survey on this).

Nevertheless, there are other control techniques that can account for such future information; for instance, Model Predictive Control (MPC) was used with the LIDAR-based preview capability for GLA in Refs. [10-13]. In Ref. [14], the authors discuss the opportunities and challenges of applying MPC for GLA. The same control technique has also been applied for other control objectives, such as wind turbine load alleviation⁽¹⁵⁾, wake vortex impact alleviation⁽¹⁶⁾, active automotive suspension⁽¹⁷⁾, ascent load management of reusable launch vehicles⁽¹⁸⁾ and obstacle avoidance⁽¹⁹⁾.

Other control techniques have also been used with the LIDAR-based preview capability to achieve different control objectives such as multi-model multi-objective optimisation feedforward control for aircraft load alleviation⁽⁷⁾, the combination of time–frequency decomposition and decentralised feedforward control for aircraft load alleviation⁽²⁰⁾, model inversion feedforward control for wake vortex impact alleviation⁽²¹⁾, model inversion feedforward control for wind turbine load alleviation⁽²²⁾ and finite-impulse-response filter feedforward control for wind turbine load alleviation⁽²³⁾.

On the other hand, the preview control technique has also been applied for control objectives such as state-feedback $H_2$ preview control for rigid aircraft load alleviation⁽²⁴⁾, affine parameter-dependent preview control for terrain following⁽²⁵⁾, adaptive preview control applied for reference tracking of missiles⁽²⁶⁾ and multi-objective preview control for active vehicle suspension⁽²⁷⁾. This preview control technique is adopted in this paper.

This paper benefits from previous work and projects but focuses on improving the controller design step. To do so, the control problem is mathematically formulated in such a way that it becomes solvable using state-of-the-art synthesis algorithms. The motivation for this work is to demonstrate the possible enhancement in the performance of GLA systems, while ensuring design flexibility and practicality for possible applications in the near future.

In Section 2, the non-linear aeroelastic model for a flexible aircraft (to which the proposed design methodology is applied) is presented. Section 3 introduces the $H_{\infty}$-optimal control problem along with its different synthesis methods, and presents the mathematical formulation of the preview control problem. In Section 4, a hands-on procedure for synthesising a GLA system based on the proposed synthesis method is given. Section 5 presents and discusses the simulation results. Section 6 draws conclusions from this work and provides recommendations for future work that could be continued.

2.0 DYNAMICS OF FLEXIBLE AIRCRAFT

Most modern aircraft feature high-aspect-ratio wings, a slender fuselage and a thin, lightweight structure, resulting in significant structural flexibility. There are two main reasons why aeroelasticity needs to be accounted for: first, the coupling between the frequencies of structural (or flexible) and rigid-body modes of the aircraft can, in the presence of non-linearities, introduce effects on the flight dynamics, leading to the degradation of performance and handling quality⁽²⁸⁾; and second, the structural modes spoil sensor measurements and can potentially reduce stability margins. Hence, the structural flexibility and structural modes have to be accounted for in the design of Flight Control Systems (FCSs). The problem of FCS–structural coupling and a proposed solution for it were discussed in more detail in Ref. [29]. The authors in Ref. [30] developed an aeroelastic model and applied it to the flight dynamics analysis of the Rockwell B-1 bomber aircraft. The mathematical model used the free vibration modes of the aircraft and was represented in the mean-axis system⁽³¹⁾ to minimise inertial coupling, while the coupling was instead captured via the aerodynamic forces. The structure of this aeroelastic model, summarised in the following paragraphs, is used in this paper.

The rigid-body dynamics of an aircraft expressed in the body axis system, the rotational kinematics expressed based on Euler angles and the translational kinematics expressed in a geodetic frame (assuming a flat, fixed Earth) can be represented by Equations (1), (2) and (3), respectively.

(1) $\begin{equation}\begin{array}{rcl}X&=&m(\dot{u}_K+q\ w_K-r\ v_K)+m\ g\sin{\Theta}\\[3pt]Y&=&m(\dot{v}_K+r\ u_K-p\ w_K)-m\ g\cos{\Theta}\sin{\Phi}\\[3pt]Z&=&m(\dot{w}_K+p\ v_K-q\ u_K)-m\ g\cos{\Theta}\cos{\Phi}\\[3pt]L&=&I_{xx}\ \dot{p}-I_{xy}(\dot{q}-p\ r)-I_{xz}(\dot{r}+p\ q)-I_{yz}\!\left(q^2-r^2\right)+(I_{zz}-I_{yy})q\ r\\[3pt]M&=&I_{yy}\ \dot{q}-I_{xy}(\dot{p}+q\ r)-I_{yz}(\dot{r}-p\ q)+I_{xz}\!\left(p^2-r^2\right)+(I_{xx}-I_{zz})p\ r\\[3pt]N&=&I_{zz}\ \dot{r}-I_{xz}(\dot{p}-q\ r)-I_{yz}(\dot{q}+p\ r)-I_{xy}\!\left(p^2-q^2\right)+(I_{yy}-I_{xx})p\ q\end{array}\end{equation}$

(2) $\begin{equation}\hspace*{-137pt}\begin{array}{rcl}\dot{\Phi}&=&p+q(\sin{\Phi}\tan{\Theta})+r(\cos{\Phi}\tan{\Theta})\\[3pt]\dot{\Theta}&=&q\cos{\Phi}-r\sin{\Phi}\\[3pt]\dot{\Psi}&=&q(\sin{\Phi}\sec{\Theta})+r(\cos{\Phi}\sec{\Theta})\end{array}\end{equation}$

(3) $\begin{equation}\hspace*{-80pt}\begin{array}{rcl}\dot{x}&=&u_K(\cos{\Theta}\cos{\Psi})\\[3pt]&&+v_K(\sin{\Phi}\sin{\Theta}\cos{\Psi}-\cos{\Phi}\sin{\Psi})\\[3pt]&&+w_K(\cos{\Phi}\sin{\Theta}\cos{\Psi}+\sin{\Phi}\sin{\Psi})\\[3pt]\dot{y}&=&u_K(\cos{\Theta}\sin{\Psi})\\[3pt]&&+v_K(\sin{\Phi}\sin{\Theta}\sin{\Psi}+\cos{\Phi}\cos{\Psi})\\[3pt]&&+w_K(\cos{\Phi}\sin{\Theta}\sin{\Psi}-\sin{\Phi}\cos{\Psi})\\[3pt]\dot{z}&=&-u_K\sin{\Theta}+v_K(\sin{\Phi}\cos{\Theta})+w_K(\cos{\Phi}\cos{\Theta})\end{array}\end{equation}$

For the structural dynamics, the total elastic displacement of the structure can be expressed in terms of a modal expansion using n free vibration modes as given by Equation (4), whereas the n generalised coordinates associated with the respective n free vibration modes are governed by the n equations given in Equation (5). By using the mean-axis system, the aeroelastic model is constituted of Equations (1), (2), (3) and (5), which are 12+n in number, have 12+2n states and are non-linear coupled differential equations of first and second order.

(4) $\begin{equation}d_E(x,y,z,t)=\sum_{i=1}^n {\big(\,\phi_i(x,y,z)\ \eta_i(t)\,\big)}\end{equation}$

(5) $\begin{equation}\ddot{\eta}_i+2\ \zeta_i\ \omega_i\ \dot{\eta}_i+\omega_i^2\ \eta_i=\frac{Q_i}{m_i}\ ,\ \ i=1,2,\ldots, n\end{equation}$

Although the current work is primarily intended to be applied to large transport aircraft (Part 25 of the FAA airworthiness standards⁽¹⁾ or CS-25 of the EASA certification specifications⁽²⁾), an aeroelastic model of a sailplane is used in this paper. The sailplane is DLR’s Discus-2c, shown in Fig. 1. The general mass and geometry characteristics, as well as the modal characteristics of the sailplane can be found in Ref. [32]. A flight test measurement system has been installed on the aircraft and allowed for the development of a non-linear aeroelastic model of the discussed structure (Equations (1), (2), (3) and (5)) in the work of Ref. [33] using system identification techniques. This allowed for the calculation of shear forces, as well as torsional and bending moments at seven load stations, of which only three (WR1, WR4 and HTR, shown in Fig. 2) are considered in this paper. The non-linear aeroelastic model accounts for the change in the local angle-of-attack of the horizontal tail due to the aircraft pitching motion as well as the time delay of the air flow reaching the horizontal tail (by delaying the downwash angle through a first-order approximation of the angle-of-attack); see Equations (5.16) and (5.17) of Ref. [33] or Equations (12) and (13) of Ref. [34] for more detail. A linear aeroelastic model to be used for the control synthesis has been obtained and validated with the non-linear aeroelastic model in Ref. [32].

Figure 1. DLR’s Discus-2c sailplane in flight.

Figure 2. Load stations and distribution of flight test sensors.

At the time of flight tests used for obtaining the non-linear aeroelastic model, no actuators were installed on the aircraft. Instead, the control surfaces were mechanically connected to the pilot’s stick, and the pilot performed the flight manoeuvres by manually manipulating the stick. If however a GLA system is to be applied, control surface actuators and automatic manipulation are required. DLR has now integrated and tested elevator and aileron actuators. On-ground and also in-flight tests have been performed to identify the elevator and aileron actuators dynamics. Based on these tests, the actuators dynamics can be well represented by the first-order dynamics given by Equation (6).

(6) $\begin{equation}\begin{array}{c}G_{\delta_e}^{\rm act} = \dfrac{\delta_{e,{\rm act}}}{\delta_{e,{\rm cmd}}} = \dfrac{1.14048}{s+1.14048},\quad G_{\delta_a}^{\rm act} = \dfrac{\delta_{a,{\rm act}}^{\rm sym}}{\delta_{a,{\rm cmd}}^{\rm sym}} = \dfrac{7.7105}{s+7.7105}\end{array}\end{equation}$

3.0 PREVIEW CONTROL

In Section 1, it was argued that, by measuring the turbulence or gusts at an adequate distance ahead of the aircraft, the performance of GLA systems can be enhanced. To achieve this, it is first required to know how to measure the turbulence or gusts and how to integrate this measured signal into the control problem. A sensor technology that enables the measurement of turbulence or gusts is Doppler LIDAR. In this type of sensor, a laser beam with a previously known wavelength/frequency is transmitted and the back-scattered light (by aerosols and/or air molecules in the atmosphere) is then received. The velocity of the aerosols/molecules – which is correlated to the air velocity – can be calculated from the Doppler shift between the frequencies of the transmitted and received laser beams. Hence, the wind speed and direction can be determined from the measurements. This paper assumes that the wind field ahead of the aircraft is available to the GLA system. Hence, the focus is rather on the optimal exploitation of this measured signal rather than on how to obtain it.

From the discussion above, it can be concluded that the sensor measures the wind at the current time but at a location that the aircraft has not yet reached. Based on the remote wind information gathered ahead of the aircraft at the present time and in the past, and based on the aircraft motion, a ‘best guess’ of the future encountered wind can be made. The control problem can then be represented by the block diagram shown in Fig. 3. From this figure, it can be seen that the future encountered wind, which the controller ‘knows’ in advance, will affect the aircraft after some time delay h.

Figure 3. Control problem with previewed disturbance.

Figure 4. Standard form for control synthesis.

The problem of structural load alleviation and ride quality enhancement of an aircraft when encountering turbulence or gusts is by nature a disturbance rejection problem. In a disturbance rejection problem, the goal is to minimise the impact of the disturbance (e.g. gust or turbulence) on the regulated outputs, whose variations in response to the disturbance must be kept as small as possible (e.g. structural loads or accelerations at various locations in the aircraft cabin). For this purpose, an adequate measure of the transfer function, i.e. a system norm, must be selected and then minimised. Two of the most widely used system norms are the $H_2$ and $H_{\infty}$ norms. The $H_2$ norm can be interpreted as an average of the system gain taken across all frequencies, whereas the $H_{\infty}$ norm is a measure of the peak gain of the system (i.e. the largest amplification that the system may show to an input vector across all frequencies and all input directions, the worst-case scenario). As the gust input is neither fixed nor has a fixed power spectrum (i.e. the objective is to minimise the peak loads), the $H_{\infty}$ norm is better suited here. Hence, the considered control problem can be well expressed as an $H_{\infty}$-optimal control design problem, shown in Fig. 4. P is the weighted plant (i.e. the plant plus the weighting functions that the control designer selects to specify the control objectives) and K is the controller to be synthesised. The objective of the $H_{\infty}$ control design problem is to find the controller K that yields a stable closed-loop system $T_{{\textbf{\textit{zw}}}}$ and ensures that its infinity norm is less than a positive $H_{\infty}$ performance value $\gamma$ (i.e. $\|T_{{\textbf{\textit{zw}}}}\|_{\infty} < \gamma$). The plant P can be expressed in state-space form as given by Equation (7), where the matrices A, $B_1$, $B_2$, $C_1$, $C_2$, $D_{11}$, $D_{12}$, $D_{21}$ and $D_{22}$ are of appropriate dimension.

(7) $\begin{align} \dot{{\textbf{\textit{x}}}}(t) & = {\textbf{\textit{A}}}\ {\textbf{\textit{x}}}(t) + {{\textbf{\textit{B}}}_1}\ {\textbf{\textit{w}}}(t) + {{\textbf{\textit{B}}}_2}\ {\textbf{\textit{u}}}(t)\nonumber\\[3pt] P :=\ {\textbf{\textit{z}}}(t) & = {{\textbf{\textit{C}}}_1}\ {\textbf{\textit{x}}}(t) + {{\textbf{\textit{D}}}_{11}}\ {\textbf{\textit{w}}}(t) + {{\textbf{\textit{D}}}_{12}}\ {\textbf{\textit{u}}}(t)\\[3pt] {\textbf{\textit{y}}}(t) & = {{\textbf{\textit{C}}}_2}\ {\textbf{\textit{x}}}(t) + {{\textbf{\textit{D}}}_{21}}\ {\textbf{\textit{w}}}(t) + {{\textbf{\textit{D}}}_{22}}\ {\textbf{\textit{u}}}(t)\nonumber\end{align}$

The classical methods for synthesising $H_{\infty}$ $ controllers (by solving either algebraic Riccati equations⁽³⁵⁾ or linear matrix inequalities⁽³⁶⁾) result in state-space controllers that have the same order as that of the weighted plant (i.e. full-order methods). To use these methods, all the system inputs and outputs should be grouped into a single channel, which can include unwanted cross-coupling terms in the overall transfer function. To overcome these disadvantages of full-order methods, researchers have investigated other methods, leading to a new $H_{\infty}$ $-optimal control method that relies on non-smooth optimisation techniques⁽³⁷⁾. The new method allows one to the choose the controller structure and order (i.e. fixed-structure method) as well as expressing the problem in a multi-channel formulation. The control problem can be illustrated in the case of two channels as shown in Fig. 5, for which an optimisation problem of the form given by Equation (8) is solved. The multi-channel formulation can be used for: first, achieving a trade-off between various $H_{\infty}$-norm criteria (in this case, the plants $P_1$, $P_2$, etc, are representing the same plant P, but with different inputs $w_i$ and outputs $z_i$; and the controllers $K_1$, $K_2$, etc, are the same controller K); and second, performing robust control design by simultaneously considering several models (e.g. corresponding to various operating points or with different values for some uncertain parameters). In this paper, both the full-order and fixed-structure methods will be used, where applicable² and compared with each other. This allows for the achievement of the required design flexibility by using the fixed-structure method while examining the optimality of the synthesised controller via comparison with that of the full-order methods.

(8) $\begin{equation}\begin{array}{l}\textrm{minimize } \quad \max\limits_{i}\left\{\left\|T_{z_{1}w_{1}}(P_1,K_1)\right\|_{\infty}\!, \left\|T_{z_{2}w_{2}}(P_2,K_2)\right\|_{\infty}\right\}\\[10pt] \textrm{subject to} \quad K_1\ \textrm{and}\ K_2\ \textrm{stabilise}\ P_1\ \textrm{and}\ P_2, \textrm{respectively} \end{array}\end{equation}$

Figure 5. Two-channel control synthesis.

Figure 6. Standard form for preview control synthesis.

The preview control problem can typically be represented by the block diagram shown in Fig. 6. The delay term can be accounted for in either the continuous⁽³⁸⁾ or discrete time⁽³⁹⁾ domains. Contrary to the continuous-time approach, the discrete-time approach provides a closed-form controller and allows the problem to be formulated in the context of full-order as well as fixed-structure methods. Hence the discrete-time approach is followed in this paper. However, in Ref. [39], the problem was formulated as a full-information state-feedback control problem and then solved using a state augmentation technique. Since in our case the model dynamics are for flexible aircraft (i.e. they include flexible degrees of freedom that cannot be measured), the problem needs to be formulated in the output-feedback setting. The same state augmentation technique is still used. A complete derivation of the preview control problem can be found in Ref. [40], which yields the discrete-time system given by Equation (9). This system is in the standard form of a $H_{\infty}$ control problem given by Equation (7), hence the characterisation of solvability relies exclusively on that of $H_{\infty}$ control theory.

(9) $\begin{align} \boldsymbol{\xi}(k+1) & = \overline{{\textbf{\textit{A}}}}\ \boldsymbol{\xi}(k) + \overline{{\textbf{\textit{B}}}}_{\boldsymbol{1}}\ {{{\textbf{\textit{d}}}_p}}(k) + \overline{{\textbf{\textit{B}}}}_{\boldsymbol{2}}\ {\textbf{\textit{u}}}(k)\nonumber\\[3pt] {\textbf{\textit{z}}}(k) & = \overline{{{\textbf{\textit{C}}}}}_{\boldsymbol{1}}\ \boldsymbol{\xi}(k) + \overline{{{\textbf{\textit{D}}}}}_{\boldsymbol{11}}\ {{{\textbf{\textit{d}}}_p}}(k) + \overline{{{\textbf{\textit{D}}}}}_{\boldsymbol{12}}\ {\textbf{\textit{u}}}(k)\\[3pt] \overline{{\textbf{\textit{y}}}}(k) & = \overline{{{\textbf{\textit{C}}}}}_{\boldsymbol{2}}\boldsymbol{\xi}(k) + \overline{{{\textbf{\textit{D}}}}}_{\boldsymbol{21}}\ {{{\textbf{\textit{d}}}_p}}(k) + \overline{{{\textbf{\textit{D}}}}}_{\boldsymbol{22}}\ {\textbf{\textit{u}}}(k)\nonumber\end{align}$

4.0 CONTROL DESIGN

4.1 Methodology

To synthesise a controller based on the synthesis method discussed in Section 3 (i.e. discrete-time $H_{\infty}$-optimal control with preview), the hands-on procedure given below is proposed. Each step of this procedure is then detailed in Subsection 4.2:

1. 1. Obtain the bare linear model of the aircraft

   1. (a) Trim the non-linear model at the desired operating point

   2. (b) Linearise the model at the trim point from the previous step

2. 2. Adjust the linear model to be in the standard form for $H_{\infty}$ control

   1. (a) If not already defined in the original non-linear model, add the exogenous disturbance inputs (without delay) to the linear model

   2. (b) Include the actuator/sensor dynamics, if not already defined in the original non-linear model

3. 3. Normalise and weight the performance channels

   1. (a) Normalise the inputs and outputs of the performance channels to obtain an open-loop $H_{\infty}$ norm $\cong 1$

   2. (b) Add the appropriate input- and control-action weighting functions

4. 4. Obtain the discrete-time preview system model

   1. (a) Discretise the model with an adequate sampling time

   2. (b) Add a chain of h unit delays (explained in more detail in Ref. [40]) to obtain the discrete-time preview system model defined in Equation (9)

   3. (c) Augment the measurement vector to include the previewed signal

5. 5. Proceed to the steps that a specific control design method may require (e.g. MATLAB’s hinfsyn or hinfstruct functions)

4.2 Application

For step 1, the chosen trim flight condition is steady rectilinear flight defined by $V_{\rm T\!AS}=$ 160km/h and $h=$ 1,000m. In this paper, only the symmetric motion and loads, the short-period mode for the rigid-body motion, as well as the first and third symmetric modes (first and second wing vertical bending, respectively) for the flexible degrees of freedom are considered. The bare linear state-space model can be defined again as given by Equation (7), but without the disturbance input w(t).

For step 2, since only the symmetric motion and loads are considered here, the exogenous disturbance input w(t) is chosen to be a vertical gust or turbulence. Assuming small angles, this vertical gust might be subtracted from the vertical component of the inertial velocity vector of the aircraft in the body axis system, $w_K(t)$. This means that the ${{\textbf{\textit{B}}}_1}$ matrix in Equation (7) will be equal to the first column of the ${\textbf{\textit{A}}}$ matrix. Since there is no direct transfer from the gust or turbulence input to the regulated outputs and measurements, the matrices ${{\textbf{\textit{D}}}_{11}}$ and ${{\textbf{\textit{D}}}_{21}}$ are set to zero matrices of appropriate dimension. Hence, the system model is written as in Equation (7).

In step 3, the regulated outputs are normalised to facilitate the expression of the design preferences. A typical method for such normalisation is to divide them by their corresponding load envelope values, which are not available to the authors. So in this work, a discrete-gust design criterion from the airworthiness standards (Section 25.341 in Ref. [1]) or certification specifications (CS 25.341 in Ref. [2]) is followed for the normalisation. According to this criterion, a gust of $1-\cos$ shape, given by Equation (10), with a sufficient number of different gust gradient distances H in the range of 30–350ft (9–107m) must be investigated to find the critical response for each load quantity. $U_{\rm ds}$ is the design gust velocity in equivalent airspeed defined by Equation (11), s is the gust penetration distance, $U_{\rm ref}$ is the reference gust velocity and $F_g$ is the flight profile alleviation factor^(1,2) . According to the criterion, $U_{\rm ref}$ is to vary linearly with altitude with $H_{\rm ref} =$ 350ft (107m). $F_g$ is assumed to be equal to $0.5$. Since this criterion is for transport aircraft but the model aircraft used for the simulation is a sailplane, H and $U_{\rm ds}$ are scaled down by the ratio of the trim speed of DLR’s Discus-2c (160km/h) to that of a transport aircraft (assumed Mach 0.5). The $1-\cos$ vertical gust input is shown in Fig. 7.

(10) $\begin{equation}U = \left\{\begin{array}{c@{\quad}c} \dfrac{U_{\rm ds}}{2}\left[1-\cos\left(\dfrac{\pi s}{H}\right)\right] & 0 \leq s \leq 2H\\[15pt] 0 & s > 2H\end{array} \right.\end{equation}$

(11) $\begin{equation} \hspace*{-46pt} U_{\rm ds} = U_{\rm ref} F_g \left(\dfrac{H}{H_{\rm ref}}\right)^{1/6}\hspace*{40pt}\end{equation}$

From Fig. 7, note that, as the gust gradient distance increases (i.e. the frequency of the $1-\cos$ gust input decreases), the amplitude increases. To reflect this in the control synthesis, a frequency-shaping function must be added to the exogenous input of the plant (the gust input here) to penalise the low-frequency inputs more than the high-frequency inputs. The appropriate weighting function can be determined from the amplitude–frequency relation at each gust gradient distance in Fig. 7. By doing so, the frequency-shaping function is given by Equation (12).

(12) $\begin{equation}\begin{array}{c}G_{w}^{F} = \dfrac{25(s+3)}{(s+2.5)(s+30)}\end{array}\end{equation}$

Finally, to achieve acceptable control actuation, high-frequency control actions should also be penalised. This can be done by weighting the control actions with some functions, and then defining them as output performance channels to be included in the computed $H_{\infty}$ norm. The functions chosen here are given by Equation (13). The final obtained continuous-time system will have a state vector of length equal to 12 (2 rigid-body states, 4 flexible degrees of freedom, 2 states for actuator dynamics, 2 states for frequency-shaping function and 2 states for control-action weighting functions).

(13) $\begin{equation}\begin{array}{c}G_{\delta_e}^{F} = \dfrac{u_{\delta_e}^{F}}{\delta_{e,{\rm cmd}}} = \dfrac{0.5(s+0.01)}{s+1},\quad G_{\delta_a}^{F} = \dfrac{u_{\delta_a^{\rm sym}}^{F}}{\delta_{a,{\rm cmd}}^{\rm sym}} = \dfrac{s+0.01}{s+7}\end{array}\end{equation}$

Figure 7. $1-\cos$ vertical gust.

Figure 8. Singular values of the frequency response.

In step 4, an adequate sampling time (or frequency) is chosen for the plant discretisation. The minimum sampling frequency at which a system can be sampled without introducing errors (also known as the Nyquist rate) should be greater than twice the highest frequency of that system. For the considered aircraft and trim condition, the highest frequency is approximately 53rad/s or 8.4Hz. This means that the minimum sampling frequency is approximately 16.8Hz, or the maximum sampling time is approximately 0.059s. This is the minimum required sampling frequency; but, to accurately capture the shape of a signal, the sampling frequency should ideally be at least ten times the highest frequency, which is $\approx$84Hz for the case considered here. This means that the sampling time must be at most $\approx$0.011s. In Fig. 8, the singular values of the frequency response of the open-loop system to the gust input are compared for two sampling times: 0.05 and 0.01s. It can be seen that, for a sampling time of 0.05s, the frequency response of the discrete-time system matches that of the continuous-time system with good accuracy only up to frequencies of $\approx$20rad/s, which is lower than the highest frequency of the system. At higher frequencies, the matching is no longer good and cannot be accepted.

This result can be confirmed by looking at the time response of the outputs of the open-loop system (for instance, the change in the bending moment at station WR1 from its trim value) to a unit-step gust input for the same two sampling times, as shown in Fig. 9. It can be seen that, in case of the sampling time of 0.05s, the shape of the signal is not accurately represented. Consequently, in this work, the sampling time is chosen to be 0.01s. The final obtained discrete-time system will be as given by Equation (9). Its state vector is composed of the original system states (here 12 states), augmented with the additional states from the h unit delays (h states). Its measurement vector ${\textbf{\textit{y}}}$ is composed of the considered feedback measurements (here $q^{\rm IMU}$ and $a_z^{\rm IMU}$), augmented with the additional measurements from the preview signal ($h+1$ measurements).

Figure 9. Time response to unit step (1m/s) vertical gust input.

5.0 RESULTS

5.1 Impact of the preview horizon on the performance of the GLA system

Normally, the structural loads on the inboard part of the wing are the highest and the most critical. This means that reducing the loads at this location allows the greatest structural weight reduction. In particular, the bending moment is the main driver for the sizing of the inboard part of the wing structure. For this reason, the bending moments at stations WR1 and WR4 are selected here. On the other hand, the aircraft locations that are very far from the aircraft CG will be exposed to the highest accelerations and load factors. Consequently, the most critical locations when considering the ride quality might be the pilot and aft-fuselage locations. Hence, the load factors at the pilot location and at station HTR are selected here as ride quality metrics. For a large transport aircraft, several locations across the cabin would have to be considered for the ride quality.

For the feedback measurements, only the pitch rate and vertical acceleration measurements of the IMU are selected. The accelerations of the wing or horizontal tail accelerometers are neglected, as normally their signals might be noisy and usually contain, among other sources of noise, undesired measurements of structural vibrations. The control effectors here are the elevator and symmetrical aileron commands. Hence, to demonstrate the possible performance enhancement of GLA systems using the proposed synthesis method of $H_{\infty}$-optimal control with preview, the problem can be formulated as shown in Fig. 10.

Figure 10. Control architecture of the synthesis problem for performance enhancement of the GLA system using previewed wind information.

The same problem is solved using the full-order method and also using the fixed-structure method. The chosen full-order method is based on solving algebraic Riccati equations using the hinfsyn function of MATLAB R2019a’s Robust Control Toolbox. As indicated by the name ‘full-order’, the obtained controller has order 12+h, which is the same order as the weighted plant; i.e. the controller order is 52 if $h=40$. The fixed-structure method provides more freedom to select any structure and order of the controller as long as it remains linear time invariant. This is particularly useful to ensure that the obtained controller can be easily implemented and gain-scheduled on a digital flight control computer. The method solves an optimisation problem using the hinfstruct function of MATLAB R2019a’s Robust Control Toolbox. The controller structure chosen here is a static gain matrix $K_{\text{static}}$ combined with two discrete-time first-order low-pass filters, as shown in Equation (14). $K_{\text{static}}$ is of size $2\times 2$ in the pure feedback case and $2\times (3+h)$ in the preview case. The discrete-time first-order filters used here correspond to low-pass filters with unit gain at low frequencies and a cutting pulsation of 5rad/s for a sampling time of 0.01s.

(14) $\begin{equation}K_{\text{structured}}(z) = \left[\begin{array}{c@{\quad}c}\displaystyle\frac{0.04877}{z - 0.95123} &0\\[12pt] 0 &\displaystyle\frac{0.04877}{z - 0.95123}\end{array}\right]\quad K_{\text{static}}\end{equation}$

Figure 11 shows the evolution of the $H_{\infty}$ performance value $\gamma$ when varying the preview length. Compared to the open-loop (OL) case, the $H_{\infty}$ norm can already be reduced using only feedback (FB) of the pitch rate $q^{\rm IMU}$ and the vertical acceleration $a_z^{\rm IMU}$. By adding the preview of the forthcoming gusts/turbulence and increasing the preview length h, further improvement can be obtained at first and then stagnates. In case of feedback only and also 0 preview length, the achieved performance with the fixed-structure method is much less than that with the full-order method. This is due to the fact that a much lower controller order is selected in the fixed-structure case in order to ensure an easy implementation of the controller afterwards. For larger preview lengths, both methods achieve almost the same performance.

Figure 11. ${H_{\infty}}$ performance value as a function of preview length for full-order and fixed-structure synthesis methods (OL: Open Loop; FB: Feedback only).

It is crucial to understand that in the previous result, all the weighting functions have been kept the same for all cases. In practice, for a given LIDAR sensor and hence a predefined preview length, the control designer will rather adjust the weighting functions (especially the ones used to penalise the control activity: $G_{\delta e}^F$ and $G_{\delta a}^F$) for making the best possible trade-off between the various design objectives.

Figures 12 and 13 show the time response of the aircraft to a $1-cosine$ gust input. It can be seen that the controller succeeded in commanding the elevator and symmetrical aileron in order to reduce the structural loads and the load factors. For the feedback only case, the controller mainly commands a negative symmetrical aileron deflection (i.e. trailing edge upward), which reduces the lift variation on the outboard of the wing, and consequently reduces the bending moment variation between the wing root and aileron stations. On the other hand, the controller was not that successful in reducing the load factors (especially at the horizontal tail station). With the preview included, the controller mainly commands positive symmetrical aileron deflection (i.e. trailing edge downward), which creates more lift, and can seem slightly counter-intuitive at first. Nevertheless, the 400 ms anticipation offered by the preview permits commanding the elevator to pitch the aircraft downwards in advance before encountering the gust, which would initiate a downwards flapping motion of the wings (compared to their steady 1g flight shape). The positive symmetrical aileron deflection however permits to alleviate this excitation of the first wing bending mode, see the time response of $\Delta \eta_1$, and thereby to reducing both the bending moments and the load factors at all stations.

Figure 12. Aircraft response to 1-cosine gust input – Part 1 (OL: Open Loop; FB: Feedback only; FBFF: Feedback-Feedforward).

Figure 13. Aircraft response to 1-cosine gust input – Part 2 (OL: Open Loop; FB: Feedback only; FBFF: Feedback-Feedforward).

Figures 12 and 13 show only the response for some selected preview lengths and one gust input, but what about the other cases? In order to show this, the same type of simulations is performed for all preview lengths and gust lengths covering the range prescribed by the certification. From all these cases, the maximum absolute value for each output is then computed and shown as bars in Fig. 14, with both the full-order and fixed-structure methods. Except for the feedback only and $h=0$ cases, the trends are similar for both methods. A significant level of load alleviation can be obtained for the bending moments at stations WR1 and WR4, with relatively short preview. However, this is obtained with fairly large elevator commands and little to no improvement in the load factor at the HTP station (which serves here as a comfort criterion for passengers seated at the back of the aircraft). With increasing the preview length, further reduction of the load factors is achieved with noticeably reduced elevator command.

Figure 14. Maximum absolute values of the regulated outputs for full-order (black) and fixed-structure (gray) synthesis methods (OL: Open Loop; FB: Feedback only). Only one light green hatched bar is shown for the open loop case as none of these controller types applies.

In conclusion, the use of a LIDAR sensor that measures the gust at a sufficient distance ahead of the aircraft enables controllers that achieve a better trade-off between structural load alleviation, comfort improvement and low control activity, even with a very simple controller consisting of a static gain matrix and two first-order low-pass filters. It is harder to achieve such a trade-off with pure feedback or local angle-of-attack measurements. In case of fewer requirements, e.g. only reduction of bending moment at station WR1, effective controllers can be designed with pure feedback or short preview lengths.

5.2 Controller robustness to changes in operating condition

One important property that the synthesised controllers must satisfy is robustness to changes in the operating conditions of the dynamic system. For an aircraft, this might be due to changes of the flight condition (e.g. flight speed, altitude, aircraft configuration and/or mass distribution). In this case, it is required to design a controller that satisfies the performance requirements even in case of such slight deviations (which might be considered as a source of uncertainty). Some ways to investigate the effect of such uncertainties on the closed-loop system stability and performance might include: (1) $\mu$-synthesis, (2) Monte Carlo simulations and (3) robustness and worst-case analysis. In this paper, however, a different approach that exploits the multi-model multi-channel formulation of the fixed-structure method is used to investigate the effect of such system uncertainties. To do so, different systems (i.e. different levels of uncertainty) are selected, and the multi-channel formulation is used to synthesise a controller that achieves acceptable performance for all the considered systems. The synthesis problem can be represented in this case as shown in Fig. 15 (with an arbitrary number of plants $P_i$, each having a different level of uncertainty).

Figure 15. Control architecture of the synthesis problem for robustness analysis.

An example of such multi-model tuning is shown for two flight conditions of DLR’s Discus-2c. The multi-channel formulation is used to synthesise the controller that achieves the overall best performance for these two flight conditions. The first flight condition is as previously defined ($V_{\rm T\!AS}=160\text{km/h}$ and $h=1,000\text{m}$), while the second is defined by $V_{\rm T\!AS}=160\text{km/h}$ and $h=3,000\text{m}$.

The enhancement of performance as a function of the preview length for the two systems is shown in Fig. 16. It can be seen that the first flight condition is the most difficult to satisfy in all cases (i.e. higher $H_{\infty}$ norm). This is not very surprising as both conditions correspond to the same true airspeed, but the first one corresponds to a slightly lower altitude, i.e. a higher equivalent airspeed. As for the previous example, the decrease of the $H_{\infty}$ norm for each output also translates into a reduction of the peak structural loads and load factors for the considered gust cases (Fig. 17). From these two figures, it can be noted that the controller is robust against the assumed uncertainties in the operating condition. A complete and detailed robustness analysis against other system uncertainties is still needed but lies beyond the scope of this paper.

Figure 16. ${H_{\infty}}$ performance value in case of different flight conditions (OL: open loop; FB: feedback only). Channel 1: $\textit{V}_{\text{T\!AS}}\,\text{=}\,\text{160}\text{km/h}$ and $\textit{h}\,\text{=}\,\text{1,000}\text{m}$. Channel 2: $\textit{V}_{\text{T\!AS}}\,\text{=}\,\text{160}\text{km/h}$ and $\textit{h}\, \text{=}\, \text{3,000}\text{m}$.

Figure 17. Maximum absolute values of the regulated outputs for first (dark blue/dark grey) and second (orange/light grey) flight conditions (OL: open loop; FB: feedback only). First flight conditions: $\textit{V}_{\text{T\!AS}}\,\text{=}\,\text{160}\text{km/h}$ and $\textit{h}\,\text{=}\,\text{1,000}\text{m}$. Second flight conditions: $\textit{V}_{\text{T\!AS}}\,\text{=}\,\text{160}\text{km/h}$ and $\textit{h}\,\text{=}\,\text{3,000}\text{m}$.

5.3 Behaviour of the GLA system towards continuous turbulence

The airworthiness standards⁽¹⁾ or certification specifications⁽²⁾ require the dynamic response of the aircraft to vertical and lateral continuous turbulence to be taken into account. Two of the most widely used continuous turbulence inputs are those with the von Kármán and the Dryden velocity spectra. Figure 18 shows a vertical continuous turbulence with the von Kármán velocity spectrum, whereas Fig. 19 shows the response of the aircraft to it. Note that the controller performs very well in case of preview (feedback-feedforward, FBFF, at $h=$ 40) in decreasing the load factor and alleviating the structural loads, with acceptable control deflections and rates.

Figure 18. Continuous turbulence with von Kármán velocity spectrum.

Figure 19. Aircraft response to the continuous turbulence with von Kármán velocity spectrum (OL: open loop; FB: feedback only; FBFF: feedback–feedforward at $\textit{h}\,\text{=}\,\text{40}$).

As could be expected after analysing the results of the discrete gust cases, the structural load alleviation of the feedback-only system as well as its capacity to reduce the vertical load factors at the front and back of the aircraft is significantly lower. Moreover, even though the pure feedback controller is far from achieving the performance level of the combined feedback-feedforward, it requires a significantly higher control command bandwidth, as can be observed from the commanded deflection rates for both the elevator ($\dot\delta_{e,{\rm cmd}}$) and symmetrical aileron ($\dot\delta_{a,{\rm cmd}}^{\rm sym}$). The maximum deflection commands are higher with the feedback-feedforward controller, but at significantly lower rates, which is a rather desirable property for decreasing the fatigue of the structure and actuators.

6.0 CONCLUSION

Based on the simulation results, the performance of the GLA system is significantly enhanced by previewing the disturbance input and actuating the control surfaces before the disturbance is encountered. The frequency-domain optimisation criteria used in this paper, which are based on the $H_{\infty}$ norm of the transfer function from the disturbance to the loads, correlates well with the peak loads obtained from the time-domain simulations to discrete gust encounters. Hence, the GLA system can be synthesised using state-of-the-art, commonly available $H_{\infty}$ control design algorithms and a disturbance rejection formulation.

Formulating the preview problem in the discrete time domain makes it easier to express it as a standard $H_{\infty}$-optimal control problem. The main design variable is the preview length h, which translates into the looking distance of the Doppler LIDAR sensor. By increasing the preview length, the controller can further reduce the structural loads and load factors until reaching a lowest value, beyond which no more performance enhancement is achievable. Design trade-offs and controller robustness are easily achieved using the multi-channel formulation of the fixed-structure synthesis method.

The controllers with a larger preview length (here 30–40 samples) showed very good load alleviation performance, whilst applying significantly more gentle commands than those with a short preview horizon or pure feedback. Such differences are particularly important for practical applications, as they would lead to less fatigue of the structure and actuators. The control synthesis criteria used here partly capture the desire for gentle/low-gain controllers through the frequency-weighted penalisation of the control actions, but additional criteria could be investigated in the future to directly penalise the fatigue at relevant locations of the airframe. This would provide finer tuning options to GLA control designers.

FUNDING SOURCES

This study was carried out during the research stay of the first author at the Institute of Flight Systems of DLR (German Aerospace Center) and was funded by the Egyptian Ministry of Higher Education and Scientific Research and the DAAD (German Academic Exchange Service, Deutscher Akademischer Austauschdienst) via the GERLS (German-Egyptian Research Longterm Scholarship) program. Special thanks go to them. The work of the second author has been funded within the frame of the Joint Technology Initiative JTI Clean Sky 2, AIRFRAME Integrated Technology Demonstrator platform ‘AIRFRAME ITD (contract no. CSJU-CS2-GAM-AIR-2014-15-01 Annex 1, Issue B04, 2 October 2015), being part of the Horizon 2020 research and Innovation framework programme of the European Commission. The methodology presented in this paper will be applied to large transport aircraft and business jets within the CleanSky2 NACOR project funded through, among many others, the aforementioned contract.