Article contents
Further Comments on Pontryagins Maximum Principle Applied to the Profile of a Beam
Published online by Cambridge University Press: 04 July 2016
Extract
Following the appearance of my note on this subject in the July 1967 JOURNAL, Professor Hemp kindly pointed out a mistake in one of the basic assumptions. This has led to a recalculation of the results, and the correct results are given below.
a width of beam
b lower bound on height of beam
d upper bound on height of beam
E Modulus of elasticity
h (x) height of beam at position x
H the Pontryagin Hamiltonian
i second moment of area=ah3/12
i length of beam
M (x) bending moment = 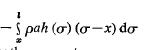
rl, r2non-dimensional length parameters
p density al lengthparam
t non-dimensional length parameter=x/l
u non-dimensional length parameter=h/l
x horizontal distance from base of beam
y (x) vertical displacement of the centre-line of beam
Y error function in hill climbing sequence
Vectors
f phase space velocity vector =dX/dt
P adjoint vector
X non-dimensional state vector
- Type
- Technical Notes
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1968
References
- 1
- Cited by


