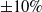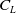Nomenclature
- b
span
-
 $C_D$
$C_D$
drag coefficient
-
 $C_L$
$C_L$
lift coefficient
-
 $C_M$
$C_M$
-
pitching moment coefficient
-
 $C_P$
$C_P$
-
pressure coefficient
- c
chord
- CG
center of gravity
- CTW
conventional tube-and-wing
- D
drag
-
 $\mathcal{D}$
$\mathcal{D}$
-
design weights
-
 $\mathcal{J}$
$\mathcal{J}$
-
objective function
- L
-
lift
-
 $L/D$
$L/D$
-
lift-to-drag ratio
- M
-
mach number
- MAC
-
mean aerodynamic chord
- MFW
-
maximum fuel weight
- MTOW
-
maximum takeoff weight
- MZFW
-
maximum zero fuel weight
- N
-
number of grid nodes
- nmi
-
nautical miles
- OEW
-
operating empty weight
- OML
-
outer mold line
- RANS
-
Reynolds-Averaged Navier Stokes
- SBW
-
strut-braced wing
- t
-
thickness
- TSFC
-
thrust specific fuel consumption
- u, v, w
-
parametric coordinates
- x, y, z
-
Cartesian coordinates
1.0 Introduction
Growing demands for a more environmentally sustainable aviation industry has motivated the search for greener aircraft technologies that can provide step changes in fuel efficiency and emissions. One promising technology is the strut-braced-wing configuration [Reference Pfenninger1], which has the potential to provide significant improvements to fuel efficiency through a high-aspect-ratio wing that is supported by a structurally efficient truss topology consisting of a main strut and sometimes one or more jury struts (i.e. the more general truss-braced wing). Given the compatibility of its unconventional wing system with conventional fuselage and empennage designs, and that the configuration leaves open the possibility of integration with many other new and emergent technologies, the strut-braced wing represents a reduced risk configuration technology that has a high potential for contributing to a more environmentally friendly aviation industry.
Given this potential, the strut- and truss-braced-wing configurations have been the focus of much research over the past few decades, with many of these investigations focusing on the design and performance of the technology through low-order multidisciplinary design optimisation (MDO) [Reference Grasmeyer, Naghshineh, Tetrault, Grossman, Haftka, Kapania, Mason and Schetz2, Reference Gern, Ko, Sulaeman, Gundlach, Kapania and Haftka3, Reference Gur, Bhatia, Schetz, Mason, Kapania and Mavris4, Reference Meadows, Schetz, Kapania, Bhatia and Seber5, Reference Mallik, Kapania and Schetz6, Reference Chakraborty, Nam, Gross, Mavris, Schetz and Kapania7] – demonstrating significant fuel burn savings for the single- and twin-aisle classes of aircraft. Recognising these potential advantages, NASA and Boeing have since initiated investigations into a Mach 0.70 truss-braced-wing single-aisle aircraft similar to the Boeing 737-800 [Reference Bradley, Droney and Allen8], with some consideration toward hybrid electric variants as well [Reference Bradley and Droney9]. Other examples include ONERA [Reference Carrier, Atinault, Dequand, Hantrais-Gervois, Liauzun, Paluch, Rodde and Toussaint10] and DLR [Reference Moerland, Pfeiffer, Böhnke, Jepsen, Freund, Liersch, Chiozzotto, Klein, Scherer, Hasan and Flink11], who investigated strut- and truss-braced-wing single-aisle aircraft at Mach 0.75 and Mach 0.72, respectively. Concerns over losses in airline productivity and compatibility with current air traffic management, however, have since motivated research into strut- and truss-braced wings at more conventional transonic speeds. For NASA and Boeing, this has culminated first in the development of a Mach 0.745 [Reference Droney, Sclafani, Harrison, Grasch and Beyar12] variant, and then a variant for Mach 0.80 [Reference Harrison, Beyar, Dickey, Hoffman, Gatlin and Viken13].
At these higher and more conventional transonic Mach numbers, however, several design challenges emerge, which must be addressed if the strut- or truss-braced-wing configuration technology is to be demonstrated as a viable option. For example, the reduced thickness and increased flexibility of the high-aspect-ratio wing can make it more vulnerable to transonic aeroelastic instabilities such as flutter [Reference Bhatia, Kapania and Haftka14]. Researchers must also consider unconventional aeroelastic deflections that are unique to the strut-braced wing topology [Reference Bartels, Funk and Scott15].
Another concern, which arises earlier in the preliminary design stage, involves the aerodynamic design of the junctions between the wing and strut(s), which emulate transonic channels that can lead to shock formation and boundary-layer separation. If not addressed, this can lead to severe drag penalties, resulting in significant reductions in the overall fuel burn savings of the configuration. Indeed, such a phenomenon can even occur at low transonic Mach numbers, which gave rise to the Platform for Aircraft Drag Reduction Innovation (PADRI) workshop, presenting a Mach 0.72 single-aisle class research platform for addressing these concerns. Some proposed solutions included passive flow control features such as the Kuchemann carrot and shock control bumps [Reference Cojocaru, Pepelea, Pricop, Nae, Stoican and Niculescu16], which echo the efforts made by Boeing to investigate strut pylons and typhoon fairings [Reference Droney, Sclafani, Harrison, Grasch and Beyar12]. While demonstrating the potential for reducing some of the adverse effects within the wing-strut junction(s), however, these approaches remain largely unproven.
As an alternative, aerodynamic shape optimisation based on the Euler or Reynolds-averaged Navier-Stokes (RANS) equations provides a means for mitigating shock formation through an automation of the shape design process that is driven by simulations of the flow physics. For methods based on the RANS equations, aerodynamic shape optimisation can also capture and address boundary-layer separation, while trading between induced drag, viscous drag and wave drag to achieve a minimum drag solution. For optimisation problem formulations with limited geometric freedom, i.e. design variables and constraints are strictly defined, aerodynamic shape optimisation can be a reliable and efficient means for refining a baseline design. Conversely, problem formulations involving more general geometric degrees of freedom and constraints can allow for a more exploratory approach to the design problem, providing the opportunity to uncover novel design features that may be more suitable for handling unconventional flow phenomena. With the adjoint method [Reference Pironneau17, Reference Jameson18] for gradient-based optimisation, such an approach to aerodynamic shape optimisation can be performed efficiently, even when considering optimisation problems with hundreds of design variables.
Some work has been done previously using high-fidelity aerodynamic shape optimisation toward the aerodynamic design challenges of the transonic strut-braced wing. For example, Gagnon and Zingg [Reference Gagnon and Zingg19] applied an optimisation method based on the Euler equations to the aerodynamic design of a Mach 0.78 strut-braced-wing regional jet, demonstrating that a low-induced drag design can be achieved with a mitigation of the adverse effects within the wing-strut junction region. Given the inviscid nature of the Euler equations, however, trades with viscous drag could not be accounted for, leaving open the question of whether a low total drag transonic strut-braced-wing aircraft can be achieved. This issue was addressed in part by a study done by Secco and Martins [Reference Secco and Martins20], which involved the application of aerodynamic shape optimisation based on the RANS equations to the PADRI strut-braced-wing geometry, demonstrating that the transonic interference effects can be largely eliminated, while achieving a lift-to-drag ratio of around 20 for the wing–strut–fuselage model. With the PADRI concept designed for Mach 0.72, however, uncertainties surrounding the aerodynamic performance of the configuration still remain at more conventional transonic Mach numbers.
Furthermore, strut- and truss-braced wings, which benefit from low-induced drag via their larger wing spans, typically prefer to operate at higher lift coefficients. This leads to a re-balancing of the induced drag and viscous drag components in order to achieve more optimal lift-to-drag ratios [Reference Turriziani, Lovell, Martin, Price, Swanson and Washburn21]. Given that the previous studies were limited to conventional lift coefficients, the question that remains to be addressed, therefore, must also consider transonic strut- and truss-braced-wing aircraft operating at higher and more optimal lift coefficients. An evaluation of the fuel efficiency of such optimised concepts must also be included, which requires an assessment of the impact that the optimised design features have on the system performance of the aircraft.
In an attempt to address these concerns, Chau and Zingg [Reference Chau and Zingg22] developed a representative Mach 0.78 strut-braced-wing regional jet based on the design missions and top level aircraft requirements of the Embraer E190-E2 through low-order conceptual MDO. Aerodynamic shape optimisation based on the RANS equations was then applied to its aerodynamic design, with results indicating that a low drag transonic design can be achieved even at a cruise lift coefficient of 0.682. With current technology levels assumed, an estimate of the block fuel over a 500nmi nominal mission demonstrated a 7.6% savings when compared to a similarly optimised conventional tube-and-wing aircraft representing the Embraer E190-E2. Such a result suggests the possibility of designing a fuel efficient transonic strut-braced-wing aircraft for the regional aircraft class. However, since transport aircraft are typically expected to maintain their performance over a range of cruise lift coefficients and Mach numbers, a more robust design is necessary, which is often achieved through on-design performance compromises for improvements at off-design conditions. This can prove to be especially challenging for the transonic strut-braced wing given its susceptibility to shock formation.
The primary objective of the present paper, therefore, is to extend the previous study by considering a range of cruise lift coefficients and Mach numbers to determine if the low-drag performance can be maintained, and to provide a more credible estimate of the fuel burn benefit offered by the transonic strut-braced-wing configuration for the regional aircraft class. Toward this end, multipoint optimisation is performed for a strut-braced-wing aircraft based on the Embraer E190-E2, as well as a conventional tube-and-wing representing the same reference aircraft for performance comparisons. Emphasis is placed on including first-order effects that have significant impacts on the design parameters of each aircraft with regard to cruise performance and block fuel. Other design considerations such as low-speed aerodynamics, high-speed buffet, and flutter, which are also important toward demonstrating the viability of the configuration, are not included, as they are expected to either impact each aircraft similarly, or to provide only higher-order effects on performance. Current technology levels will also be assumed in order to focus on the benefits of the configuration technology itself. As a secondary objective, the present paper will also investigate the aerodynamic design features that contribute to a successful transonic strut-braced-wing regional jet, with comparisons between single-point and multipoint optimised designs.
The paper is organised as follows. Section 2 provides an overview of the approach for evaluating the relative fuel burn performance of the transonic strut-braced-wing configuration, while Section 3 presents the aircraft characteristics of the strut-braced-wing and conventional tube-and-wing regional jets. The high-fidelity aerodynamic shape optimisation framework used to perform multipoint optimisation is described in Section 4, with the optimisation problem formulations included in Section 5. Results, and conclusions and future work are presented in Sections 6 and 7, respectively.
2.0 Approach to evaluating aircraft fuel efficiency
Representative aircraft concepts are developed through the application of a conceptual MDO framework [Reference Chau and Zingg22], which consists of low-order models for aerodynamics, structures, weight and balance, propulsion and performance – providing a means for capturing most of the first-order effects that are relevant to cruise performance and block fuel. The objective of each MDO problem is to achieve a minimum block fuel design over a nominal range mission at a cruise Mach number of 0.78. This represents a typically flown mission for the Embraer E190-E2, and is separate from the design missions used to size the design weights of each aircraft, as described in Ref. [Reference Chau and Zingg22].
For the strut-braced-wing concept, design variables are focused on the sizing and optimisation of the wing, strut, horizontal and vertical tails, propulsion system, and operating conditions. For the wing and tail systems, design variables include the root and tip chord lengths and thickness-to-chord ratios of each wing, strut and tail segment. Constraints on these degrees of freedom include a maximum design wing loading, which places a lower bound on the wing area for takeoff and landing considerations based on the Embraer E190-E2; a minimum fuel volume, which maintains a minimum wing and strut outer mold line (OML) for the fuel tanks based on the maximum fuel weight (MFW); and minimum tail volume ratios based on a reference T-tail design. Other wing and strut parameters such as span, sweep and dihedral, as well as the attachment locations of the strut with the wing and fuselage, are not included since they are assumed to have a strong dependence on structures and aeroelastic phenomena such as flutter, going beyond the capabilities of the low-order models. These parameters are set based on reference concepts found in Bradley et al. [Reference Bradley, Droney and Allen8].
Another design variable for the strut-braced-wing concept is a maximum thrust parameter for resizing the propulsion system, which is constrained by a minimum thrust-to-weight ratio also based on the Embraer E190-E2, and top-of-climb excess thrust requirements. Initial cruise altitude design variables are also included for each design mission, which help determine the optimum cruise
![]() $C_L$
values for minimum block fuel over the nominal mission. These design variables are constrained by a number of disciplinary effects such as the thrust required at top-of-climb, and tradeoffs with climb fuel.
$C_L$
values for minimum block fuel over the nominal mission. These design variables are constrained by a number of disciplinary effects such as the thrust required at top-of-climb, and tradeoffs with climb fuel.
For the conventional tube-and-wing configuration, a concept is developed as-drawn, namely, the wing, horizontal and vertical tails, propulsion systems, and operating conditions are defined as closely as possible to the Embraer E190-E2. Given that the wing thickness-to-chord ratios are not publicly available, however, these are included as design variables and are driven toward a minimum block fuel solution while subject to a minimum fuel volume constraint.
Other design considerations for the strut-braced-wing concept include an assumption that the strut produces minimal lift, and hence is developed primarily as a structural member that generates as little drag as possible. The structures of the wing and strut are also constructed from composite materials, which is a technology that is readily available and provides an advantage over the aluminum wing composition of the Embraer E190-E2-like conventional tube-and-wing. Technologies such as natural laminar flow, active flow control, and advanced propulsion systems are not considered, given the objective of isolating the benefit offered by the configuration technology when assuming current technology levels. Additional details on the conceptual design of each aircraft are provided in Chau and Zingg [Reference Chau and Zingg22].
These concepts are used to create 3D models of each aircraft that include the wing (and strut), fuselage, and horizontal tail. This allows for a multipoint optimisation of each wing and tail system that captures the dominant aerodynamic effects, including the lift and interference drag from the presence of the fuselage. The optimisation of each aircraft is performed for a range of lift coefficients and Mach numbers that include and surround the nominal cruise point. To enable a more exploratory approach to design optimisation, a more general formulation of the constraints is employed to maintain the feasibility of each aircraft. For example, minimum wing (and strut) volume and minimum maximum thickness-to-chord ratio constraints are defined, which together act as surrogates for maintaining a minimum structural depth of the wing (and strut) that is independent of the internal structural topology. These constraints also ensure that there is sufficient volume for containing the fuel tanks required to store the MFW.
A construction of the full aircraft performance is then accomplished through a synthesis of the high-fidelity aerodynamic estimates with low-fidelity approximations from the components not modeled in the RANS simulations. The updated cruise fuel approximation can then be combined with the approximations for warmup, taxi, takeoff, climb, descent and landing to provide an estimate of the mission block fuel for each aircraft.
3.0 Aircraft characteristics
Aircraft concepts representing the strut-braced-wing and conventional tube-and-wing configurations in the regional jet class, herein referred to as the SBW100 and CTW100, respectively, are developed based on the design missions and top level aircraft requirements of the Embraer E190-E2. This includes a design range and payload of 3,100nmi and 104 passengers, respectively. As described in Section 2, however, evaluations of cruise performance and block fuel consider a nominal mission with a range of 500nmi, the design payload and a Mach number of 0.78. Planform views of the aircraft concepts are shown in Fig. 1.

Figure 1. Aircraft concepts developed through conceptual MDO [Reference Chau and Zingg22].
Table 1 provides an overview of the aircraft characteristics and their nominal performance based on the low-order models. Compared to the CTW100, the SBW100 has the advantage of a 60% larger wing aspect ratio, which trades efficiently against penalties in added wing wetted area. In order to realise the full potential of this high aspect ratio wing, however, the SBW100 must operate at a much higher cruise
![]() $C_L$
. For a given wing loading, this results in a significantly elevated cruise altitude. It is important to note, however, that achieving the optimum lift coefficient for maximising the lift-to-drag ratio must trade with increased climb fuel and potentially higher fuselage weights as a result of increased cabin pressurisation loads. These factors are accounted for in the conceptual design process, with the design
$C_L$
. For a given wing loading, this results in a significantly elevated cruise altitude. It is important to note, however, that achieving the optimum lift coefficient for maximising the lift-to-drag ratio must trade with increased climb fuel and potentially higher fuselage weights as a result of increased cabin pressurisation loads. These factors are accounted for in the conceptual design process, with the design
![]() $C_L$
of the SBW100 representing the optimum
$C_L$
of the SBW100 representing the optimum
![]() $C_L$
for minimum block fuel.
$C_L$
for minimum block fuel.
The SBW100 also has the advantage of a 24.5% lower wing weight compared to the CTW100 owing to the structural efficiency of the strut-bracing and the benefit of composite structures. This is offset, however, by an 11.9% heavier fuselage, which comes from weight penalties for fuselage-mounted landing gears and a larger horizontal tail moment arm, which translates to larger fuselage bending loads in the empirical equations. Together, the aerodynamic and structural advantages combine to provide an overall reduction in the design weights of the SBW100. For more details on the aircraft concepts developed through the low-order MDO framework, see Chau and Zingg [Reference Chau and Zingg22].
4.0 High-fidelity aerodynamic shape optimisation framework
The high-fidelity aerodynamic design of each aircraft is performed through the application of an aerodynamic shape optimisation framework called Jetstream that has been developed at the University of Toronto Institute for Aerospace Studies. It consists of an integrated geometry parameterisation and mesh-deformation scheme [Reference Hicken and Zingg23, Reference Osusky, Buckley, Reist and Zingg24], a free-form and axial deformation geometry control system [Reference Gagnon and Zingg25], a structured multiblock Newton-Krylov-Schur flow solver for the RANS equations fully coupled with the Spalart-Allmaras turbulent model [Reference Osusky and Zingg26], the discrete-adjoint method for flow- and mesh-dependent gradient evaluation [Reference Pironneau17, Reference Jameson18], and SNOPT [Reference Gill, Murray and Saunders27] for gradient-based optimisation. In the following sections, a brief description of each component is provided.
Table 1. Aircraft characteristics from conceptual MDO.

a All operating conditions and cruise parameters are in reference to the start of cruise for the nominal mission.
4.1 Integrated mesh parameterisation and deformation
In order to update the computational grid following a deformation to the aerodynamic surfaces, Jetstream includes an integrated mesh parameterisation and deformation scheme [Reference Hicken and Zingg23, Reference Osusky, Buckley, Reist and Zingg24] that can achieve large shape changes at a relatively low computational cost, while maintaining the quality of the grid. Given an initial structured multiblock mesh associated with a given baseline geometry, each block is parameterised with cubic B-spline volumes through a chord-length parameterisation. This provides a parametric model of the mesh that closely approximates the initial computational grid, and by extension, the aerodynamic surfaces, which maintains consistency throughout the optimisation process. In addition, this parametric model also provides a means of automatically refining the computational grid through grid node insertion and redistribution [Reference Osusky, Buckley, Reist and Zingg24]. This capability is used in the present work to generate a consistent family of grid levels for performing grid convergence studies.
For mesh deformation, a linear elasticity model is applied to each B-spline volume in parallel, where deformations applied to the subset of surface control points defining the aerodynamic surfaces are propagated across each control volume within the computational domain. In order to preserve the quality of the computational grid, the stiffness of each element within a given block is defined to be proportional to its volume and a measure of its orthogonality [Reference Hicken and Zingg23]. To accommodate large shape changes, robustness can be further improved by subdividing the deformation into smaller increments of linear elastic changes, thus maintaining the small strain assumption and allowing for intermediate updates to the element stiffnesses. With the number of B-spline volume control points being 2–3 orders less than the number of nodes in the computational mesh, the deformation of the complete CFD mesh can be achieved at a significantly lower computational cost.
4.2 Geometry control
For controlling the shape of the aerodynamic surfaces, a free-form and axial deformation method [Reference Gagnon and Zingg25] is used in which free-form deformation (FFD) volumes provide local or sectional design control and axial curves provide global or planform design control. These FFD volumes are defined as B-spline volumes that can be manipulated through their control points to smoothly deform an embedded object of interest, while the axial curves, defined as B-spline curves, can be similarly controlled to drive the position and orientation of these FFD volumes in space. Within the Jetstream framework, the surface control points that define the aerodynamic surfaces to be deformed are embedded within the FFD volumes rather than their surface discretisations. This results in an efficient two-level deformation system in which geometry control is dissociated from shape representation, maintaining the analytical surface and mesh definitions.
To reduce the number of degrees of freedom to a smaller set of more intuitive design variables, the x-, y- and z-coordinates of the FFD volume control points are used to define section shape, as well as twist and taper degrees of freedom. These are defined through rotation and scaling operators applied to each FFD-volume cross-section as follows:
-
• Twist: a rotation of the FFD-volume cross-section in the local xz-plane about the local origin
-
• Taper: a uniform scaling of the FFD-volume cross-section in the local xz-plane with respect to the local origin
-
• Section Shape: a scaling of the vertical distance from the local origin to the position of a given FFD-volume control point along the local z-axis; this design variable is defined separately for each individual FFD-volume control point
These transformation operators are applied to the initial xyz-coordinates of each FFD-volume cross-section in sequence at each design iteration and follow a cubic interpolation between each FFD-volume control point in the parametric chordwise direction u, a cubic interpolation between each FFD-volume cross-section in the parametric spanwise direction v, and a linear interpolation between each FFD-volume control point pair in the parametric vertical direction w, where the parametric coordinates follow the transformation
![]() $\mathcal{F}(u,v,w) \rightarrow (x,y,z)$
.
$\mathcal{F}(u,v,w) \rightarrow (x,y,z)$
.
Attached to each FFD volume is an axial curve that passes through each FFD-volume cross-section and is typically positioned at the leading edge, quarter chord or trailing edge of a given wing object. Since the FFD-volume cross-sections must remain attached and normal to their associated axial curve based on their initial attachment locations, the axial curves can be manipulated to provide more global changes to the embedded object. The axial curves also define the origins of each local coordinate system with which the FFD volume design variables are defined. These local coordinate systems are oriented with their xz-axes in-plane with each FFD-volume cross-section. In the present paper, the axial curves are primarily used to serve this purpose, and so are generally only defined as linear B-spline curves. In general, however, they can be defined as B-spline curves of any order, and can be manipulated through sweep, span and dihedral degrees of freedom that are defined through translation operators. Specifically, these design variables are defined as follows:
-
• Sweep: a translation in the x-coordinate of a given axial curve control point
-
• Span: a translation in the y-coordinate of a given axial curve control point
-
• Dihedral: a translation in the z-coordinate of a given axial curve control point
For more details on the geometry control system, see Gagnon and Zingg [Reference Gagnon and Zingg25] and Chau and Zingg [Reference Chau and Zingg22].
4.3 Flow solver
To calculate aerodynamic functionals, Jetstream uses a parallel implicit Newton-Krylov-Schur algorithm [Reference Osusky and Zingg26] for solving the RANS equations fully coupled with the Spalart-Allmaras turbulence model (SA). More specifically, SA-neg [Reference Allmaras, Johnson and Spalart28] is used in conjunction with QCR2000 (29), the latter of which is included to aid in properly resolving flow separation in and around junction regions [Reference Levy, Laflin, Tinoco, Vassberg, Mani, Rider, Rumsey, Wahls, Morrison, Brodersen, Crippa, Mavriplis and Murayama30].
Second-order spatial discretisation is provided by centered difference summation-by-parts (SBP) operators [Reference Del Rey Fernández, Hicken and Zingg31] coupled with simultaneous approximation terms (SATs) to enforce boundary conditions and couple block interfaces weakly. Artificial dissipation is included in the form of 2nd-difference and 4th-difference scalar dissipation operators to improve numerical convergence, with the introduction of the 2nd-difference artificial dissipation controlled by a pressure sensor.
The numerical solution to the linearised governing equations is driven toward steady state via an inexact-Newton method. Globalisation of the flow solution is performed through pseudo-transient continuation, with the linear system that arises at each Newton iteration solved inexactly using a flexible variant of the Krylov subspace method, generalised minimal residual (GMRES) [Reference Saad and Schultz32, Reference Saad33], preconditioned with the approximate-Schur method [Reference Saad and Sosonkina34].
This flow solver has been validated against results from the Fifth Drag Prediction Workshop (DPW5) [Reference Levy, Laflin, Tinoco, Vassberg, Mani, Rider, Rumsey, Wahls, Morrison, Brodersen, Crippa, Mavriplis and Murayama30], with the predicted drag coefficient of the NASA Common Research Model (CRM) agreeing within one drag count of the median across all participants [Reference Osusky, Boom and Zingg35]. In the present work, boundary layers are assumed to be fully turbulent.
4.4 Gradient evaluation and optimisation
Numerical optimisation is performed with SNOPT [Reference Gill, Murray and Saunders27], a gradient-based optimisation algorithm based on the sequential quadratic programming (SQP) paradigm that can handle large-scale constrained optimisation problems with both linear and nonlinear constraints. For gradient evaluation, Jetstream uses the discrete-adjoint method [Reference Pironneau17, Reference Jameson18] for the computation of the objective function gradient, as well as constraint gradients that depend directly on the flow or mesh-deformation equations. For all other constraint gradients, which are predominantly associated with geometric constraints, and sensitivities that contribute to the discrete-adjoint method, analytical calculations are performed, with some quantities approximated through the complex-step method [Reference Squire and Trapp36]. For more details on the gradient evaluation method, see Osusky et al. [Reference Osusky, Buckley, Reist and Zingg24].
5.0 Optimisation problem setup
In the following sections, the problem setup for each high-fidelity aerodynamic shape optimisation is presented. This includes a description of the baseline geometries, which not only serve as the initial designs for each gradient-based optimisation problem, but also determine some of the design variable bounds as described in Section 4.2. An overview of the computational grids, which have been developed to balance grid resolution and computational cost, is also provided. Sections 5.3 and 5.4 then present the multipoint optimisation formulations, and the design variables and constraints, respectively.
5.1 Baseline geometries
For optimisation, the baseline geometries include the wing (and strut), fuselage, and horizontal tail components, with the overall dimensions based on the conceptual designs presented in Section 3. For both aircraft, the fuselage nose and tail sections are modeled based on the OML of the Airbus A220-300 [37]. Similarly, the wing-fuselage fairing for the CTW100 is also modeled based on the A220-300 and scaled to the dimensions of that of the Embraer E190-E2. For the SBW100, however, the wing-fuselage and strut-fuselage fairings are based on those of the PADRI strut-braced-wing geometry [Reference Bieler, Bier, Bugeda, Periaux, Redondo, Guttila and Pons38], and are repositioned along the fuselage in reference to the concepts presented in Bradley et al. [Reference Bradley, Droney and Allen8].
For both aircraft, the baseline wing geometries are defined by RAE-2822 aerofoil profiles, which provide reasonable starting points for transonic wing design. Symmetric supercritical SC(2)-0012 sections are used for the strut of the SBW100, while SC(2)-0010 profiles are used for the horizontal tail of each aircraft.
5.2 Computational grids
For performing aerodynamic analyses, structured multiblock grids are created for each aircraft model, which are characterised by O-H blocking topologies, i.e. O- and H-grid blocking topologies in the near- and far-fields, respectively. For the CTW100, the optimisation-level grid consists of 14.41 million nodes distributed across 558 blocks, while for the SBW100, there are 26.51 million nodes over 1,355 blocks. The difference in the number of blocks, and by extension the number of grid nodes for a similar maximum number of nodes per block, is due to how the number of blocks scales with geometric complexity. The SBW100 grid also includes a local O-O blocking topology surrounding the strut, where the second O-grid layer projects onto the lower surface of the wing. This provides the necessary boundary of surface patches used to decouple the deformations of the wing and strut where they intersect with one another, as described in Section 5.4.
These optimisation level grids have been generated following the medium mesh gridding guidelines of the Fourth Drag Prediction Workshop (DPW), which are representative of current drag prediction standards [Reference Vassberg, Tinoco, Mani, Rider, Zickuhr, Levy, Brodersen, Eisfeld, Crippa, Wahls, Morrison, Mavriplis and Murayama39]. In general, this resolution offers a reasonable tradeoff between computational cost and accuracy, while including sufficient grid resolution for capturing the relevant flow features. In order to obtain mesh-independent aerodynamic functionals for the initial and optimised designs, Richardson extrapolation is performed with the addition of two finer grid levels, L1 and L2, which have two and four times as many grid nodes as the optimisation-level grid L0, respectively. Table 2 provides an overview of the grid characteristics, with off-wall spacings and
![]() $y^+$
values in reference to the initial designs.
$y^+$
values in reference to the initial designs.
Table 2. Grid information. Optimisation is performed on the L0 grid levels, while the L0-L1-L2 grid families are used to perform grid convergence studies.

a Off-wall spacings are in units of mean aerodynamic chord.
b Maximum average values across each set of design points.
5.3 Multipoint objective
A common approach to multipoint optimisation for the aerodynamic design of an aircraft is to formulate the objective function as a weighted integral over a range of operating conditions in order to improve robustness at off-design conditions across a range of operating parameters [Reference Buckley and Zingg40]. For example, a weighted integral over the Mach number and
![]() $C_L$
design space can be defined as
$C_L$
design space can be defined as
 \begin{equation} \mathcal{J} = \int\limits_{C_{L_1}}^{C_{L_2}}\int\limits_{M_1}^{M_2} \mathcal{D}(M,C_L)\ C_D(M,C_L)\ \mathrm{d}M\mathrm{d}C_L\end{equation}
\begin{equation} \mathcal{J} = \int\limits_{C_{L_1}}^{C_{L_2}}\int\limits_{M_1}^{M_2} \mathcal{D}(M,C_L)\ C_D(M,C_L)\ \mathrm{d}M\mathrm{d}C_L\end{equation}
where
![]() $\mathcal{D}(M,C_L)$
are user-defined design weights that can be used to place more priority on nominal operating points that are expected to be encountered more frequently over the operating envelope. This integral can be approximated through a quadrature method given by [Reference Li, Huyse and Padula41]
$\mathcal{D}(M,C_L)$
are user-defined design weights that can be used to place more priority on nominal operating points that are expected to be encountered more frequently over the operating envelope. This integral can be approximated through a quadrature method given by [Reference Li, Huyse and Padula41]
 \begin{equation} \mathcal{J} = \sum\limits_{i=1}^{N_{C_L}}\sum\limits_{j=1}^{N_M} w_{i,j}\ \mathcal{D}(M_i,C_{L_j})\ C_D(M_i,C_{L_j}) \approx \int\limits_{C_{L_1}}^{C_{L_2}}\int\limits_{M_1}^{M_2} \mathcal{D}(M,C_L)\ C_D(M,C_L)\ \mathrm{d}M\mathrm{d}C_L\end{equation}
\begin{equation} \mathcal{J} = \sum\limits_{i=1}^{N_{C_L}}\sum\limits_{j=1}^{N_M} w_{i,j}\ \mathcal{D}(M_i,C_{L_j})\ C_D(M_i,C_{L_j}) \approx \int\limits_{C_{L_1}}^{C_{L_2}}\int\limits_{M_1}^{M_2} \mathcal{D}(M,C_L)\ C_D(M,C_L)\ \mathrm{d}M\mathrm{d}C_L\end{equation}
where
![]() $w_{i,j}$
are the weights of the quadrature method. This approach is useful when aerodynamic shape optimisation is used in the context of designing a real and very robust aircraft, especially when the nominal design point is complemented by other design points that provide constraints related to low-speed aerodynamics, high-speed buffet and flutter. In the present paper, however, the objective is to assess the relative performance of the transonic strut-braced-wing configuration while accounting for a range of cruise conditions, especially at higher Mach numbers with respect to the nominal value of 0.78, and while ignoring higher-order effects. For this purpose, it is sufficient and less costly to consider a small and discrete set of operating conditions that includes multiple
$w_{i,j}$
are the weights of the quadrature method. This approach is useful when aerodynamic shape optimisation is used in the context of designing a real and very robust aircraft, especially when the nominal design point is complemented by other design points that provide constraints related to low-speed aerodynamics, high-speed buffet and flutter. In the present paper, however, the objective is to assess the relative performance of the transonic strut-braced-wing configuration while accounting for a range of cruise conditions, especially at higher Mach numbers with respect to the nominal value of 0.78, and while ignoring higher-order effects. For this purpose, it is sufficient and less costly to consider a small and discrete set of operating conditions that includes multiple
![]() $C_L$
values and higher Mach numbers. Although point-optimisation at each of the design points can lead to excessively optimistic estimates of the overall performance of a given aircraft, several studies have suggested that robust designs can be achieved with a modest number of discrete operating conditions in a multipoint optimisation problem formulation [Reference Nemec, Zingg and Pulliam42, Reference Kenway and Martins43].
$C_L$
values and higher Mach numbers. Although point-optimisation at each of the design points can lead to excessively optimistic estimates of the overall performance of a given aircraft, several studies have suggested that robust designs can be achieved with a modest number of discrete operating conditions in a multipoint optimisation problem formulation [Reference Nemec, Zingg and Pulliam42, Reference Kenway and Martins43].
To this end, a five-point multipoint optimisation is considered that consists of the nominal operating point, two operating points subjected to a
![]() $\pm 10\%$
change in
$\pm 10\%$
change in
![]() $C_L$
from the nominal point, and two high-speed conditions with a
$C_L$
from the nominal point, and two high-speed conditions with a
![]() $+0.03$
change in Mach number from the nominal point at
$+0.03$
change in Mach number from the nominal point at
![]() $-10\%$
and
$-10\%$
and
![]() $-20\%$
$-20\%$
![]() $C_L$
. These design points cover a range of expected operating conditions with an emphasis on those most likely to lead to significant wave drag penalties. The objective function is then given by
$C_L$
. These design points cover a range of expected operating conditions with an emphasis on those most likely to lead to significant wave drag penalties. The objective function is then given by
where the design weights are selected such that the nominal operating condition has a two-fold priority over all other design points. The design points considered are listed in Table 3.
Table 3. Single-point [Reference Chau and Zingg22] and multipoint optimisation design weights and operating conditions.

5.4 Design variables and constraints
Design variables include the angle-of-attack, as well as geometric degrees of freedom provided by the free-form and axial deformation geometry control systems shown in Fig. 2. For the CTW100, the parameterised wing and horizontal tail are each embedded within FFD volumes with 12 and 4 FFD-volume cross-sections, respectively, each consisting of 11 FFD-volume control point pairs. For the wing, these provide twist and section shape design variables, while for the horizontal tail, section shape design variables are omitted to maintain a symmetric design, and the twist design variables are linked across the FFD volume to provide incidence angle control. Axial curves are positioned at the quarter chord of each FFD volume, and hence each lifting surface, which define the local coordinate system for the twist and section shape design variables.

Figure 2. Geometry control systems with FFD volume entities in blue, and axial curve entities in fuschia.
A similar setup is used for the SBW100. The FFD volume of the wing consists of 19 FFD-volume cross-sections for the same number of cross-sections per unit span, with additional cross-sections introduced near the wing-strut junction to provide sufficient geometric control for addressing the transonic interference effects. Additional FFD volumes are also included to embed the main and vertical strut surfaces, as well as the transition strut, which connects the end of the main strut to the start of the vertical strut. These strut segments are shown in the inset of Fig. 2(b). As with the CTW100, each FFD-volume cross-section consists of 11 control point pairs, which provide twist and section shape design variables for the wing and strut. The incidence angle of the horizontal tail is also included as a design variable, and axial curves are positioned at the quarter chord of each lifting surface.
A novel junction deformation scheme is also included to enable the optimisation of the wing-strut junction where the geometry control system of the wing and strut intersect [Reference Chau and Zingg22]. Similar junction deformation schemes are also included at each fuselage intersection, where changes in the geometry over the embedded aerodynamic surfaces are propagated across the fuselage patches of each aircraft [Reference Osusky, Buckley, Reist and Zingg24]. This allows for changes to the overall incidence angle of each lifting surface, and is specifically used to define the incidence angle degree of freedom for each horizontal tail. Table 4 provides a summary of the design variables involved in each problem, as well as their bounds.
For simulating steady, level flight, each multipoint optimisation problem includes nonlinear constraints for maintaining a constant lift and zero pitching moment. The pitching moment constraint, which would be considered at all operating conditions if elevators were modeled, is included only at the nominal design point for each aircraft. As mentioned in Section 2, minimum volume and minimum
![]() $(t/c)_\mathrm{max}$
constraints are also included, which take the form of nonlinear constraints.
$(t/c)_\mathrm{max}$
constraints are also included, which take the form of nonlinear constraints.
A number of linear geometric constraints are also included to further constrain the design space. For example, the minimum distance between each chordwise pair of FFD-volume control points is limited to 50% of its baseline value, while fixed leading- and trailing-edge constraints are included to prevent shear twist and the translation of each FFD-volume cross-section. Other linear geometric constraints are included to help simplify the design of the strut near the wing-strut junction. These include a constant twist constraint for the vertical strut FFD-volume cross-sections, and a linear interpolation twist constraint across the FFD-volume cross-sections of the transition strut. A linear interpolation twist constraint is also applied across the three wing FFD-volume cross-sections across the wing-strut junction to prevent the optimiser from introducing a very sudden wash-in to compensate for the local loss of sectional lift caused by the presence of the strut. A summary of the linear and nonlinear constraints is provided in Table 5.
Table 4. Design variable information.

a SBW100 wing root and vertical strut twist bounds are limited to
![]() $\pm3.5$
deg.
$\pm3.5$
deg.
Table 5. Linear and nonlinear constraint information.

6.0 Optimisation results
The SNOPT optimisation histories for each multipoint optimisation problem are shown in Fig. 3. The parameters are Optimality – a measure of the objective function and constraint gradients, Feasibility – a measure of the constraint violations, and the Merit Function, which represents the objective function when constraint violations are minimised. Each optimisation is considered converged when the Merit Function changes by less than a drag count over 10 or more function evaluations, Optimality has been reduced by approximately two or more orders of magnitude, and Feasibility has been satisfied to a tolerance of at least
![]() 10$^{-4}$
. For both cases, these requirements are met following 55–60 major iterations or 60–70 function evaluations, with more than 95% of the drag reductions achieved within the first 25–30 major iterations.
10$^{-4}$
. For both cases, these requirements are met following 55–60 major iterations or 60–70 function evaluations, with more than 95% of the drag reductions achieved within the first 25–30 major iterations.
In order to obtain accurate predictions of the cruise drag at each design point of each multipoint optimised design, grid-converged
![]() $C_D$
values are estimated through Richardson extrapolation, using the L0, L1, and L2 grid levels described in Section 5.2. The data points are shown in Fig. 4, where the convergence of
$C_D$
values are estimated through Richardson extrapolation, using the L0, L1, and L2 grid levels described in Section 5.2. The data points are shown in Fig. 4, where the convergence of
![]() $C_D$
is monotonic for all cases. This is a necessary condition for the application of Richardson extrapolation. Although the errors in
$C_D$
is monotonic for all cases. This is a necessary condition for the application of Richardson extrapolation. Although the errors in
![]() $C_D$
associated with the L0 grid level are seen to be significant,
$C_D$
associated with the L0 grid level are seen to be significant,
![]() $C_D$
converges consistently across each grid level, and the relative performance is maintained as the grids are refined. As such, the multipoint optimised designs obtained on the L0 grid level can be expected to be closely comparable to those optimised on a finer grid level. For comparisons, Fig. 4 also includes grid convergence studies for the single-point optimised designs, evaluated at each design point. The estimates of the grid-converged
$C_D$
converges consistently across each grid level, and the relative performance is maintained as the grids are refined. As such, the multipoint optimised designs obtained on the L0 grid level can be expected to be closely comparable to those optimised on a finer grid level. For comparisons, Fig. 4 also includes grid convergence studies for the single-point optimised designs, evaluated at each design point. The estimates of the grid-converged
![]() $C_D$
values provide objective function values of
$C_D$
values provide objective function values of
![]() $\mathcal{J} = 217$
counts and
$\mathcal{J} = 217$
counts and
![]() $\mathcal{J} = 208$
counts for the single-point and multipoint optimised CTW100 designs, respectively, and
$\mathcal{J} = 208$
counts for the single-point and multipoint optimised CTW100 designs, respectively, and
![]() $\mathcal{J} = 289$
counts and
$\mathcal{J} = 289$
counts and
![]() $\mathcal{J} = 277$
counts for the single-point and multipoint optimised SBW100 designs, respectively.
$\mathcal{J} = 277$
counts for the single-point and multipoint optimised SBW100 designs, respectively.
Table 6 includes the aerodynamic performance of each multipoint optimised aircraft, with results from the single-point optimisations of Chau and Zingg [Reference Chau and Zingg22] also included for comparisons. Based on the high-fidelity models of each aircraft, the results indicate that the multipoint optimised SBW100 provides a 9.8% improvement in cruise
![]() $L/D$
and a 13.2% reduction in cruise drag over the multipoint optimised CTW100. Compared to the single-point optimised designs, the multipoint optimums show a similar relative benefit with a 0.3% improvement in both cruise
$L/D$
and a 13.2% reduction in cruise drag over the multipoint optimised CTW100. Compared to the single-point optimised designs, the multipoint optimums show a similar relative benefit with a 0.3% improvement in both cruise
![]() $L/D$
and drag at the nominal design point, despite an increase in
$L/D$
and drag at the nominal design point, despite an increase in
![]() $C_D$
by 2 counts for both aircraft.
$C_D$
by 2 counts for both aircraft.

Figure 3. SNOPT optimisation histories.

Figure 4. Grid convergence studies for the single-point and multipoint optimised designs at constant lift, evaluated at each of the five design points. Drag coefficients at
![]() $N^{-2/3} = 0$
are obtained from Richardson extrapolation.
$N^{-2/3} = 0$
are obtained from Richardson extrapolation.
Table 6. Optimised aircraft performance at the nominal design point.

a Includes only the wing (and strut), fuselage, and horizontal tail contributions.
b Includes a 5% excrescence drag markup, and profile drag contributions from the vertical tail, nacelles and pylons.
In order to obtain estimates for the full aircraft performance, low-order approximations for the drag of the aircraft components not included in the high-fidelity models are introduced, namely, for the vertical tail, nacelles and pylons of each aircraft. Skin friction drag mark-ups of 5% are also applied to approximate contributions from airframe excrescences. These results are also presented in Table 6 and indicate a 13.1% improvement in cruise
![]() $L/D$
and a 15.7% reduction in cruise drag at the nominal design point for the multipoint optimised SBW100, relative to the similarly optimised CTW100. Compared to the single-point optimised aircraft, this represents a 0.2% improvement in both relative aircraft cruise
$L/D$
and a 15.7% reduction in cruise drag at the nominal design point for the multipoint optimised SBW100, relative to the similarly optimised CTW100. Compared to the single-point optimised aircraft, this represents a 0.2% improvement in both relative aircraft cruise
![]() $L/D$
and drag. These results suggest that a low drag strut-braced wing can be achieved over a range of cruise conditions, especially since the performance benefits appear to be robust to off-design conditions at higher Mach numbers and lift coefficients.
$L/D$
and drag. These results suggest that a low drag strut-braced wing can be achieved over a range of cruise conditions, especially since the performance benefits appear to be robust to off-design conditions at higher Mach numbers and lift coefficients.
For approximating the block fuel for each nominal range mission, estimates of weight and TSFC are calculated through the low-order models, along with the fuel contributions from warmup, taxi, takeoff, climb, descent and landing, which are assumed to remain constant. This provides a block fuel savings of 7.8% for the multipoint optimised SBW100 when compared to the Embraer E190-E2-like CTW100. Compared to the aircraft designs obtained from single-point optimisation, this represents a further relative reduction of 0.2% since the drag increase experienced by the CTW100 when designed for multiple cruise conditions is marginally higher than that of the SBW100.
Comparisons of the drag performance between the single-point and multipoint optimised designs over the five design points of each aircraft are shown in Fig. 5. Here, it can be seen that the nominal performance degradation of 2 drag counts for both aircraft leads to an improvement in aerodynamic performance at the off-design conditions. For design points 2 and 3, the performance improvements are on the order of 1% and 2.5%, respectively, for each aircraft, while improvements of approximately 10–12% are achieved at design points 4 and 5. This illustrates that for both aircraft, a low drag can be maintained at the off-design cruise conditions, with significant improvements specifically at the high-speed design points, without the introduction of significant compromises to on-design performance.

Figure 5. Cruise drag performance at each design point of the five-point operating envelope for each optimised design.
Table 7 presents approximations for the full aircraft performance of each aircraft at each of the design points. These results are obtained by adjusting the fixed weight of each aircraft at each operating condition such that the start of cruise
![]() $C_L$
matches the
$C_L$
matches the
![]() $C_L$
of each design point. Changes to the weight of the aircraft due to changes in the fuel required at warmup, taxi, takeoff, climb, descent and landing, as well as to the fuel reserves, are accounted for. Overall, the improvements in cruise
$C_L$
of each design point. Changes to the weight of the aircraft due to changes in the fuel required at warmup, taxi, takeoff, climb, descent and landing, as well as to the fuel reserves, are accounted for. Overall, the improvements in cruise
![]() $L/D$
and drag at the off-design conditions range from 14–16% and 11–13.5%, respectively. From Fig. 6, the savings in block fuel obtained for the missions associated with each design point remain consistent at around 7–8%.
$L/D$
and drag at the off-design conditions range from 14–16% and 11–13.5%, respectively. From Fig. 6, the savings in block fuel obtained for the missions associated with each design point remain consistent at around 7–8%.
Table 7. Multipoint optimised aircraft performance at the on- and off-design operating conditions.


Figure 6. Multipoint optimised block fuel burn comparisons at on- and off-design operating conditions.
Figure 7 shows the multipoint optimised spanwise lift distributions for each aircraft operating at the nominal design point, with those of the single-point optimised designs included for comparisons. For all cases, the optimised net spanwise lift distributions are elliptical in form but shifted inboard due to the presence of the trim constraint and the presumed avoidance of high outboard sectional lift coefficients that can lead to increased wave drag penalties. Moreover, the multipoint optimised spanwise lift distributions feature further inboard shifts, which are compensated by modest increases in the negative lift over each horizontal tail. Of interest, however, is that for the multipoint optimised SBW100, the inboard shift is the result of a moderate increase in positive lift over the strut, which allows the main wing to reduce its loading. This feature likely enables an improvement in performance over the high-speed design points where the cruise
![]() $C_L$
values are much lower, while aiding in reducing the overall wing loading for the high
$C_L$
values are much lower, while aiding in reducing the overall wing loading for the high
![]() $C_L$
design point. Such a benefit suggests that lifting struts are aerodynamically favourable for transonic strut-braced wings, and may explain in part why Boeing has opted to incorporate and emphasie such a feature when transitioning from their Mach 0.70 design [Reference Bradley, Droney and Allen8] to their Mach 0.745 [Reference Droney, Sclafani, Harrison, Grasch and Beyar12] and Mach 0.80 variants [Reference Harrison, Beyar, Dickey, Hoffman, Gatlin and Viken13]. It should be noted, however, that lifting struts can lead to structural design challenges associated with the impact of non-axial loads on buckling.
$C_L$
design point. Such a benefit suggests that lifting struts are aerodynamically favourable for transonic strut-braced wings, and may explain in part why Boeing has opted to incorporate and emphasie such a feature when transitioning from their Mach 0.70 design [Reference Bradley, Droney and Allen8] to their Mach 0.745 [Reference Droney, Sclafani, Harrison, Grasch and Beyar12] and Mach 0.80 variants [Reference Harrison, Beyar, Dickey, Hoffman, Gatlin and Viken13]. It should be noted, however, that lifting struts can lead to structural design challenges associated with the impact of non-axial loads on buckling.

Figure 7. Optimised spanwise lift distributions computed on the L0 grid level.

Figure 8. CTW100: Optimised design and flow features computed on the L0 grid level at the nominal design point (
![]() $M = 0.78$
and
$M = 0.78$
and
![]() $C_L = 0.468$
).
$C_L = 0.468$
).

Figure 9. CTW100: Optimised aerofoil profiles and pressure distributions at two off-design cruise conditions computed on the L0 grid level.

Figure 10. SBW100: Optimised design and flow features calculated on the L0 grid level at the nominal design point (
![]() $M = 0.78$
and
$M = 0.78$
and
![]() $C_L = 0.682$
).
$C_L = 0.682$
).

Figure 11. SBW100: Optimised aerofoil profiles and pressure distributions at two off-design cruise conditions computed on the L0 grid level.

Figure 12. SBW100: Surface pressure contours with inner ((a),left) and outer ((a),right) views of the strut, and aerofoil profiles and pressure distributions at different stations along the wing and strut. Results are for the nominal design point on the L0 grid level.
Additional aerodynamic design features are presented next, first for the CTW100 and then for the SBW100. For the CTW100, an overview of the multipoint optimised design features and flow characteristics at the nominal design point is shown in Fig. 8, with the single-point optimisation results included for comparisons. From Fig. 8(a), it can be seen that the optimiser has allowed some shock surfaces to return over the upper surface of the wing, although these shocks are relatively weak with upstream Mach numbers less than Mach 1.1. This is consistent with the relatively small drag increase of 2 counts when optimising for multiple design points rather than one. Figure 8(c) shows optimised aerofoil profiles and pressure distributions at different spanwise stations across the wing. At the majority of the spanwise stations, the leading-edge suction peaks are reduced to favour more aft loading. At stations
![]() $2y/b = 30\%$
, 45%, and 60%, a noticeable decrease in mid-chord loading can also be seen, which may be tied to the more favourable aerodynamic performance at the off-design cruise conditions.
$2y/b = 30\%$
, 45%, and 60%, a noticeable decrease in mid-chord loading can also be seen, which may be tied to the more favourable aerodynamic performance at the off-design cruise conditions.
Figure 9 shows the single-point and multipoint optimised aerofoil profiles and pressure distributions at the same spanwise locations, but for design points 2 and 4, which are two of the more challenging off-design cruise conditions. For the
![]() $+10\%\;C_L$
design point, the pressure distributions are similar in form to those of the nominal design point, except here, it can also be seen that their features contribute to significant reductions in the strength of the shocks present over the single-point optimised design. For the pressure distributions at the Mach 0.81 design point, it can be seen that the design features help in reducing the suction peak while also reducing the favourable pressure gradient that begins near 50% chord and terminates around 65% chord. This also results in a shock strength reduction.
$+10\%\;C_L$
design point, the pressure distributions are similar in form to those of the nominal design point, except here, it can also be seen that their features contribute to significant reductions in the strength of the shocks present over the single-point optimised design. For the pressure distributions at the Mach 0.81 design point, it can be seen that the design features help in reducing the suction peak while also reducing the favourable pressure gradient that begins near 50% chord and terminates around 65% chord. This also results in a shock strength reduction.
An overview of the design features and flow characteristics for the multipoint optimised SBW100 is provided in Fig. 10, with the single-point optimised design and flow features included for comparisons. As with the CTW100 optimisations, the multipoint optimised design experiences an increase in wave drag due to the return of shocks over the wing upper surface. Once again, however, the upstream Mach numbers associated with these shock surfaces are all less than Mach 1.1, indicating that they are weak and have a small effect on drag. Shock surfaces present within the junction of the baseline wing and strut presented in Chau and Zingg [Reference Chau and Zingg22] also remain eliminated for the multipoint optimised SBW100, even when accommodations are made to preserve off-design aerodynamic performance. Based on the pressure distributions, it can be seen that the weak shocks over the wing are positioned close to 50% chord. For the strut, the pressure distribution at 15% semispan illustrates an increase in lift, which is achieved through a minor increase in geometric twist.
Figure 11 shows the pressure distributions for the high
![]() $C_L$
design point, as well as those of the first high-speed cruise condition. Here, the same trends as those of the CTW100 can be observed, but with the pressure distributions adjusted to compensate for the higher overall lift requirements. In fact, the multipoint optimised pressure distributions suggest a higher wave drag penalty based on the magnitude of the change in pressure coefficient over the steep pressure recovery regions when compared to those of the CTW100. However, the total drag savings offered by the SBW100 suggests that this penalty is outweighed by savings in induced and viscous drag. At the high-speed design point, the pressure distributions are also quite similar to those of the CTW100. As expected, the lift carried by the strut also appears to scale with
$C_L$
design point, as well as those of the first high-speed cruise condition. Here, the same trends as those of the CTW100 can be observed, but with the pressure distributions adjusted to compensate for the higher overall lift requirements. In fact, the multipoint optimised pressure distributions suggest a higher wave drag penalty based on the magnitude of the change in pressure coefficient over the steep pressure recovery regions when compared to those of the CTW100. However, the total drag savings offered by the SBW100 suggests that this penalty is outweighed by savings in induced and viscous drag. At the high-speed design point, the pressure distributions are also quite similar to those of the CTW100. As expected, the lift carried by the strut also appears to scale with
![]() $C_L$
.
$C_L$
.
Inner and outer views of the wing-strut junction designs from single-point and multipoint optimisation are shown in Fig. 12. These include surface pressure distributions, as well as aerofoil profiles and pressure distributions at four stations along the wing, and four stations along the transition and vertical strut segments. For clarity, these aerofoil profiles have not been rotated with respect to the angle-of-attack, as has been done in the previous figures. Here, the surface pressures at the nominal cruise condition are generally smooth and free of adverse effects for both designs. This is consistent with the absence of shocks within the junction region shown in Fig. 10. The overall section designs are also quite similar between the two optimisations. For the wing, exceptions include small differences in aerofoil shape toward the leading edge as seen in sections C and D, and an overall reduction in sectional lift, corresponding to the reduction in wing loading observed in the spanwise lift distributions. For the strut, a minor reduction in outwards force distribution can be seen for the multipoint optimum. The overall similarities between the single-point and multipoint optimised designs indicate that both the novel aerofoil shapes, and the outwards force distribution are not necessarily point-designed features, and are likely to be key contributors to low drag transonic strut-braced-wing designs that are more robust to changes in operating conditions.
7.0 Conclusions and future work
Toward a more credible estimate of the fuel burn benefit associated with the transonic strut-braced-wing configuration at conventional Mach numbers, and higher and more optimal lift coefficients, this paper presents an investigation of a Mach 0.78 strut-braced-wing regional jet with a lift coefficient of 0.682 through the application of multipoint aerodynamic shape optimisation based on the RANS equations. This aircraft is developed as a representative concept for the configuration based on the design missions and top-level aircraft requirements of the Embraer E190-E2 through the application of a low-order conceptual design environment. For performance comparisons, a conventional tube-and-wing aircraft is also included, which represents the Embraer E190-E2 as a modern best-in-class regional jet.
Given the importance of addressing the transonic interference effects of the strut-braced wing, which become more difficult to overcome at high transonic Mach numbers, the present paper considers multipoint optimisation with the nominal design point, design points at
![]() $\pm 10\%$
nominal
$\pm 10\%$
nominal
![]() $C_L$
at Mach 0.78, and two Mach 0.81 design points at
$C_L$
at Mach 0.78, and two Mach 0.81 design points at
![]() $-10\%$
and
$-10\%$
and
![]() $-20\%$
nominal
$-20\%$
nominal
![]() $C_L$
. These optimisations consider the wing–body–tail models of each aircraft, with results indicating that low drag performance at each design point can be maintained, achieving up to 10–12% reductions in off-design cruise drag compared to single-point optimised designs, while only compromising on-design performance by less than 1%.
$C_L$
. These optimisations consider the wing–body–tail models of each aircraft, with results indicating that low drag performance at each design point can be maintained, achieving up to 10–12% reductions in off-design cruise drag compared to single-point optimised designs, while only compromising on-design performance by less than 1%.
Aerodynamic design features that contribute to the robustness and efficiency of the transonic strut-braced wing include an outwards force distribution over the strut near the wing-strut junction, and novel wing sections, which together aid in mitigating the transonic channel effect, and hence shock formation and boundary-layer separation. Away from the wing-strut junction region, the optimised strut-braced wing is found to feature a moderately lifting strut, which enables a reduction in inboard wing loading for improving aerodynamic performance at higher Mach numbers and higher lift coefficients.
Introducing low-order estimates for constructing approximations for full aircraft performance that include drag contributions from the vertical tails, nacelles and pylons, the transonic strut-braced-wing regional jet is found to provide a 13.1% improvement in cruise lift-to-drag ratio over the similarly optimised conventional tube-and-wing aircraft. Further introducing low-order estimates for the fuel required for warmup, taxi, takeoff, climb, descent and landing, this translates to a 7.8% savings in block fuel over a 500nmi nominal mission. Similar fuel burn savings are maintained over each of the off-design conditions, with estimates ranging from 7 to 8%.
Given the relatively high cruise altitudes needed to achieve the optimal design
![]() $C_L$
, one would expect a larger fuel burn benefit when considering a longer range nominal mission. For example, as a first-order estimate, updates to the low-order approximations, namely, the non-aerodynamics and non-cruise block fuel contributions, results in a relative fuel burn benefit of 10.8% for a 1,000nmi mission. Another consideration is the question of how much of a benefit is attributed to the advantage of composites. Given that the CTW100 is intended to represent the Embraer E190-E2, its wing structures were modeled with aerospace-grade aluminum. However, if a variant of the CTW100 is considered with a composite wing structure, low-order approximations indicate that the relative fuel burn benefit of the multipoint optimised SBW100 reduces to 6.8% for the nominal range mission.
$C_L$
, one would expect a larger fuel burn benefit when considering a longer range nominal mission. For example, as a first-order estimate, updates to the low-order approximations, namely, the non-aerodynamics and non-cruise block fuel contributions, results in a relative fuel burn benefit of 10.8% for a 1,000nmi mission. Another consideration is the question of how much of a benefit is attributed to the advantage of composites. Given that the CTW100 is intended to represent the Embraer E190-E2, its wing structures were modeled with aerospace-grade aluminum. However, if a variant of the CTW100 is considered with a composite wing structure, low-order approximations indicate that the relative fuel burn benefit of the multipoint optimised SBW100 reduces to 6.8% for the nominal range mission.
For further improving the reliability of fuel burn estimates associated with the transonic strut-braced-wing configuration for the regional aircraft class, future work will include high-fidelity aerostructural optimisation for investigating parameters such as wing span and sweep, and wing-strut junction location, as well as the advantages of adding one or more jury struts. Toward this end, transonic flutter will also be considered. For further developing the concept as a transport aircraft, future work will include considerations toward high-speed buffet and low-speed performance. Other future work will investigate the advantages of the transonic strut-braced-wing configuration for the single-aisle class of aircraft.
As a final note, it may be worth considering the potential impact of interference drag from the engine nacelles interacting with the strut surfaces. Although such an effect may be avoidable for larger aircraft where there is sufficient vertical distance toward the wing and strut roots to provide clearance, this may not be the case for regional jets with relatively large diameter turbofan engines. In these instances, it is recommended that this effect be accounted for in a future work.
Acknowledgements
Financial support is provided in part by the Natural Sciences and Engineering Research Council of Canada, the Queen Elizabeth II Graduate Scholarship in Science and Technology, the Ontario Graduate Scholarship, and the University of Toronto. Computations were performed on the Niagara supercomputer at the SciNet High-Performance Computing Consortium. SciNet is funded by the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; the Ontario Research Fund – Research Excellence; and the University of Toronto.