Article contents
Buckling and Vibration of Isosceles Triangular Plates having the Two Equal Edges Clamped and the Other Edge Simply–Supported
Published online by Cambridge University Press: 28 July 2016
Extract
Approximate Solutions obtained by the method of collocation are presented for the lowest critical buckling load of an isosceles triangular plate loaded as shown in Fig. 1. Also, the fundamental frequency is given. The base of the triangle is simply supported and the other equal edges are clamped. The usual assumptions regarding the bending of thin plates are made. The governing differential equation for the plate loaded as shown in Fig. 1 is
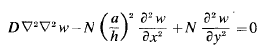 1
1
where D is the plate stiffness, N is axial load per unit length, w is deflection, positive downward, and the quantities a and h are dimensions shown in Fig.1.
- Type
- Technical Notes
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1955
References
- 1
- Cited by


