Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T06:36:48.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Aerofoil nose shapes delaying leading-edge separation

Published online by Cambridge University Press:  04 July 2016

E. O. Tuck  and
A. Dostovalova
E. O. Tuck
Affiliation:
University of Adelaide, Australia
A. Dostovalova
Affiliation:
University of Adelaide, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

If an aerofoil of chord c has a parabolic nose with radius of curvature r, and is placed at angle-of-attack α to a stream, the laminar boundary layer on its upper surface remains unseparated for α<0.8l8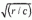. In the present paper we consider some smooth local modifications to the leading edge. Symmetric modifications of the nature of local sharpening of the nose can improve this result to at least α<0.897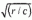. Further improvements are possible for unsymmetrical (e.g. drooped) noses, and an example of a ‘drooped’ nose with α<0.912 is shown.

Type
Research Article
Information
The Aeronautical Journal , Volume 104 , Issue 1039 , September 2000 , pp. 433 - 437
Copyright
Copyright © Royal Aeronautical Society 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Anderson, J.D., Corda, S. and Van Wie, D.M. Numerical lifting line theory applied to drooped leading-edge wings below and above stall, J Aircr, 1980, 17, pp 898–904.Google Scholar
2. Ruban, A.I. Asymptotic theory of short separation regions on the leading edge of a slender aerofoil, Izv Ak Nauk SSSR Mekh Zhidk, Gaza, 1981, 1, pp 42–51. (English translation pp 33-41.Google Scholar
3. Tuck, E.O. A criterion for leading edge separation, J Fluid Mech, 1991, 222, pp 33–37 Google Scholar
4. Abbott, I.H. and Von Doenhoff, A.E. Theory of Wing Sections, Dover, New York, 1959.Google Scholar
5. Werle, M.J. and Davis, R.T. Incompressible laminar boundary layers on a parabola at angle-of-attack: a study of the separation point, Trans ASME E: J Appl Mech, 1972, pp 7–12.Google Scholar
6. Keller, H.B. Numerical methods in boundary-layer theory, Ann Rev Fluid Mech, 1978, 10, pp 417–433.Google Scholar