Article contents
Verification & validation of lifting line  $\alpha $- and
$\alpha $- and 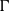 $\Gamma $-formulations for 3-D planforms under viscous flows
$\Gamma $-formulations for 3-D planforms under viscous flows
Published online by Cambridge University Press: 02 March 2023
Abstract
Many adaptations of the lifting-line theory have been developed since its conception to aid in preliminary aerodynamic wing design, but they typically fall into two main formulations, named  $\alpha $- and
$\alpha $- and 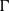 $\Gamma $-formulation, which differ in terms of the control points chordwise location and the variable updated during the iterative scheme. This paper assess the advantages and drawbacks of both formulations through the implementation of the respective methods and application of standard verification and validation procedures. Verification showed that the
$\Gamma $-formulation, which differ in terms of the control points chordwise location and the variable updated during the iterative scheme. This paper assess the advantages and drawbacks of both formulations through the implementation of the respective methods and application of standard verification and validation procedures. Verification showed that the 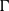 $\Gamma $-method poorly converges for wings with nonstraight quarter-chord lines, while the
$\Gamma $-method poorly converges for wings with nonstraight quarter-chord lines, while the  $\alpha $-method presents adequate convergence rates and uncertainties for all geometries; it also showed that the
$\alpha $-method presents adequate convergence rates and uncertainties for all geometries; it also showed that the 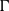 $\Gamma $-method agrees best with analytic results from the cassic lifting-line theory, indicating that it tends to overpredict wing lift. Validation and comparison to other modern lifting-line methods was done for similar geometries, and not only corroborated the poor converge and lift overprediction of the
$\Gamma $-method agrees best with analytic results from the cassic lifting-line theory, indicating that it tends to overpredict wing lift. Validation and comparison to other modern lifting-line methods was done for similar geometries, and not only corroborated the poor converge and lift overprediction of the  $\Gamma $-method, but also showed that the
$\Gamma $-method, but also showed that the  $\alpha $-method presented the closest results to experimental data for almost all cases tested, concluding that this formulation is typically superior regardless of the wing geometry. These results indicate that the implemented
$\alpha $-method presented the closest results to experimental data for almost all cases tested, concluding that this formulation is typically superior regardless of the wing geometry. These results indicate that the implemented  $\alpha $-method has a greater potential for the extension of the lifting-line theory to more geometrically complex lifting surfaces other than fixed wings with straight quarter-chord lines and wakes constrained to the planform plane.
$\alpha $-method has a greater potential for the extension of the lifting-line theory to more geometrically complex lifting surfaces other than fixed wings with straight quarter-chord lines and wakes constrained to the planform plane.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Royal Aeronautical Society
References
- 1
- Cited by



