Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T03:27:05.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Aircraft dynamics optimisation via linear matrix inequalities

Published online by Cambridge University Press:  04 July 2016

G. Mengali
G. Mengali*
Affiliation:
Department of Aerospace Engineering University of Pisa, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the problem of determining an optimal controller which minimises the 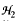norm of a given aircraft while guaranteeing that an upper limit of its 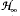norm is not exceeded. The problem is tackled by means of a linear matrix inequality formulation, which allows one to constrain the eigenvalues of the model to within a fixed region of the complex plane. Key features of the method are the possibility of simultaneously

  • 1. keeping the maximum value of the input demand under control

  • 2. taking flying quality requirements into account

  • 3. assuring a minimum level of system robustness against uncertainties of the model.

The approach is simple to handle and is well suited to the design of aircraft stability augmentation systems. A discussion of two case studies demonstrates the effectiveness of the procedure.

Type
Research Article
Information
The Aeronautical Journal , Volume 100 , Issue 998 , October 1996 , pp. 313 - 320
Copyright
Copyright © Royal Aeronautical Society 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Moore, B.C. On the Flexibility offered by state feedback in multi- variable systems beyond closed loop eigenvalue assignment, IEEE Transact Auto Contr,October 1976, AC-21, (5), pp 689–692.Google Scholar
2. Srinathkumar, S. Eigenvalue/eigenvector assignment using output feedback, IEEE Transact Auto Contr, January 1978, AC-23, (1), pp 79–81.Google Scholar
3. Andry, A.N., Shapiro, E.J. and Chung, J.C. Eigenstructure assign ment for linear systems, IEEE Transact Aero and Electr Sys, September 1983, AES-19, (5), pp 711–729.Google Scholar
4. Sobel, K.M. and Shapiro, EJ. Application of eigenstructure assignment to flight control design: some extensions, J Guid Contr Dynam, 1987, 10, (1), pp 73–81.Google Scholar
5. Mudge, S.K. and Patton, R.J. Analysis of the technique of robust Eigenstructure assignment with application to aircraft control, In: IEE Proceedings, PtD, July 1988, 135, (4), pp 275–281.Google Scholar
6. Garrard, W.L., Low, E. and Proudy, S. Design of attitude and rate command systems for helicopters using Eigenstructure assignment, J Guid Contr Dynam, 1989, 12, (6), pp 783–791.Google Scholar
7. Low, E. and Garrard, W.L. Design of flight control systems to meet rotorcraft handling qualities specifications, J Guid Contr Dynam, 1993, 16, (1), pp 69–78.Google Scholar
8. Boyd, S., El gaoui, L., Feron, E. and Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory, Siam Books, Philadelphia, 1994.Google Scholar
9. Chilali, M. and Gahinet, P. , design with pole placement constraint: an LMI approach. In: Proc IEEE Conf Decision and Control, 1994, pp 553–558.Google Scholar
10. Gahinet, P. Explicit controller formulas for LMI-based synthesis, In: Proc American Control Conference, 1994, pp 2396–2400.Google Scholar
11. Iwasaki, T. and Skelton, R.E. All controllers for the general . control problem: LMI existence conditions and state space formulas, Automatica, 1994, 30, (8), pp 1307–1317.Google Scholar
12. ANON Flying Qualities of Piloted Airplanes, Military Specification, MIL-F-8785 C, 1980.Google Scholar
13. Desoer, C.A. and Vidyasagar, M. Feedback Systems: Input-Output Properties, Academic Press, New York, 1975.Google Scholar
14. Francis, B.A. A course in Control Theory, Lecture Notes in Control and Information Sciences, Springer-Verlag, Berlin, 1987, 88.Google Scholar
15. Bernstein, D. and Haddad, W.M. Lqg control with an performance bound: a Riccati equation approach, IEEE Transact Auto Cont, March 1989, AC-34, (3), pp 293–305.Google Scholar
16. Khargonekar, P.P. and Rotea, M.A. Mixed /control: a convex optimization approach, IEEE Transact Auto Contr, July 1991. AC-36, (7), pp 824–837.Google Scholar
17. Doyle, J.C, Packard, A. and Zhou, K. Review of LFTs, LMIs andμ, In: Proc. IEEE Conf Decision and Control, 1991, pp 1227–1232.Google Scholar
18. Doyle, J.C, Glover, K., Khargonekar, P.P. and Francis, B.A. State-space solutions to standard and control problems, IEEE Transact Auto Cont, August 1989, AC-34, (8), pp 831–847.Google Scholar
19. Bryson, A.E. and Ho, Y.C. Applied Optimal Control, Hemisphere, Washington DC, 1975.Google Scholar
20. Scherer, C. -optimization without the assumption on finite or infinite zeros, SIAM J Contr Opt, January 1992, 30, (1), pp 143–166.Google Scholar
21. Gahinet, P., Nemirovski, A., Laub, A.J. and Chilali, M. LMI Control Toolbox, The MathWorks, Natick, Mass, 1995.Google Scholar
22. Mengali, G. Ride quality improvements by means of numerical optimization techniques, J Guid Contr Dynam, 1994, 17, (5), pp 1037–1041.Google Scholar
23. Sadoff, M., Bray, R.S. and Andrews, W.H. Summary of NASA research on jet transport control problems in severe turbulence, JAircr, March 1966, 3, (3), pp 193–200.Google Scholar
24. Apkarian, P., Biannic, J.M. and Gahinet, P. Self-scheduled control of missile via linear matrix inequalities, J Guid Contr Dynam, May-June 1995, 18, (3), pp 532–538.Google Scholar
25. Wang, W. and Safonov, M.G. A tighter relative error bound for balanced stochastic truncation, Sys Contr Letters, 1990, 14, pp 307–317.Google Scholar
26. Anderson, B.D.O. and Liu, Y. Controller reduction: concepts and approaches, IEEE Transact Auto Cont, August 1989, AC-34, (8), pp 802–812.Google Scholar