Article contents
Aerofoil nose shapes delaying leading-edge separation
Published online by Cambridge University Press: 04 July 2016
Abstract
If an aerofoil of chord c has a parabolic nose with radius of curvature r, and is placed at angle-of-attack α to a stream, the laminar boundary layer on its upper surface remains unseparated for α<0.8l8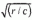 . In the present paper we consider some smooth local modifications to the leading edge. Symmetric modifications of the nature of local sharpening of the nose can improve this result to at least α<0.897
. In the present paper we consider some smooth local modifications to the leading edge. Symmetric modifications of the nature of local sharpening of the nose can improve this result to at least α<0.897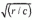 . Further improvements are possible for unsymmetrical (e.g. drooped) noses, and an example of a ‘drooped’ nose with α<0.912
. Further improvements are possible for unsymmetrical (e.g. drooped) noses, and an example of a ‘drooped’ nose with α<0.912 is shown.
is shown.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1979
References
- 1
- Cited by


