Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T12:36:11.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Profile Fitting by the Interference Function

Published online by Cambridge University Press:  06 March 2019

Luca Lutterotti  and
Paolo Scardi
Luca Lutterotti
Affiliation:
Department of Materials Engineering, University of Trento 38050 Mesiano (TN), (Italy)
Paolo Scardi
Affiliation:
Department of Materials Engineering, University of Trento 38050 Mesiano (TN), (Italy)
Get access

Abstract

On the basis of the “column-like” powder model of Warren and Averbach, a profile fitting procedure was devised to obtain microstructural disorder parameters. The interference function

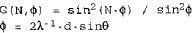
where d is the interplanar distance, λ the wavelength, θ the diffraction angle and N the number of cells within a column, was used to model experimental profiles taking into account the column-like crystallite size and r.m.s. strain distributions. The procedure can be applied both to single peak and to two or more peaks of multiple order of reflection. The method was tested on several samples, also having a bimodal size distribution, and the results compared with those obtained by the well-established Warren-Averbach analysis.

Type
VIII. XRD Profile Fitting, Crystallite Size and Strain Determination
Information
Advances in X-Ray Analysis , Volume 35 , Issue A: First Pacific-International Congress on X-ray Analytical Methods (PICXAM). Fortieth Annual Conference on Applications of X-ray Analysis, August 7-16, 1991 , 1991 , pp. 577 - 584
Copyright
Copyright © International Centre for Diffraction Data 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Warren, B.E. & Averbach, B.L., J. Appl. Phys. 21:595 (1950).Google Scholar
2. Warren, B.E. & Averbach, B.L., J. Appl. Phys. 23:1059 (1952).Google Scholar
3. Klug, H.P. & Alexander, L.E., 1974, “X-Ray Diffraction Procedures for Polycrystalline and Amorphous Materials,” 2nd ed., pp. 643–655, J. Wiley & Sons, New York (1974).Google Scholar
4. Enzo, S., Fagherazzi, G., Benedetti, A. & Polizzi, S., J. Appl. Cryst. 21:536 (1988).Google Scholar
5. Benedetti, A., Fagherazzi, G.,Enzo, S. & Battagliarin, M., J .Appl .Cryst. 21:543 (1988) .Google Scholar
6. Guérin, D. M. A., Alvarez, A.G., RebollO Neira, L. E., Plastino, A. & Bonetto, R.D., J. Appl. Cryst. A42:30 (1986).Google Scholar
7. Adler, T. & Houska, C.R., J. Appl.Phys. 50 :3282 (1979).Google Scholar
8. Scardi, P., Lutterotti, L. & R. Di Maggio, Powder Diffraction 6:20 (1991)Google Scholar
9. Scardi, P., Lutterotti, L. R. Di Maggio & p. Maistrelli, in: “Proceeding of the First European Powder Diffraction Conference-EPDICl, Munich (FRG) , March 14-l6th, 1991”. To be published on Mat. Sci. Forum.Google Scholar
10. Rietveld, H.M., Acta Cryst., 22:151 (1967).Google Scholar
11. Rietveld, H.M., Acta Cryst. 2:65 (1969) .Google Scholar
12. Lutterotti, L. & scardi, P., J. Appl. Cryst. 23:246 (1990).Google Scholar