Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T20:22:16.775Z Has data issue: false hasContentIssue false
  • English
  • Français

An Accurate Coefficient Method for X-Ray Fluorescence Analysis

Published online by Cambridge University Press:  06 March 2019

E. Tertian
E. Tertian*
Affiliation:
Rhône-Poulenc Industries 93308 Aubervilliers, France
Get access

Abstract

Performing highly automated, computerized X-ray spectrometric analysis ‘without standards’ calls for accurate matrix correction programs which can be based, essentially, on either the ‘fundamental parameter’ method or improved influence coefficient procedures. The coefficient scheme discussed in this paper was devised to strictly comply with the theoretical relationships for X-ray fluorescence emission, thus connecting, in a way, both approaches. This result is achieved by accurately making allowance for the two complicating factors affecting fluorescent intensities i.e. : (1) the mobility of coefficients, and (2) the occurrence of fluorescence crossed effects. The corresponding algorithm, for practical use, writes

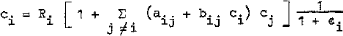
where the (aij + bij ci) terms account for the individual influence coefficients and their variation, and ϵi refers to the overall crossed effect. The essential problem of calibration is then considered, with special emphasis being laid on : (a) experimental coefficient determination, and (b) experimental crossed effect evaluation. Current coefficient methods are briefly surveyed in relation to the present theory.

Finally, the advantages of an experimental, accurate coefficient procedure over the fundamental parameter approach, from a practical standpoint, are emphasized.

Type
Mathematical Correction Procedures for X-Ray Spectrochemical Analysis
Information
Advances in X-Ray Analysis , Volume 19: Twenty-Fourth Annual Conference on Applications of X-ray Analysis, August 6-8, 1975 , 1975 , pp. 85 - 111
Copyright
Copyright © International Centre for Diffraction Data 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Sherman, J., “The Correlation between Fluorescent X-ray Intensity and Chemical Composition”, ASTM Special Technical Publication 157, 27–33 (1954).Google Scholar
2. Beattie, H.J. and Brissey, R.M., “Calibration Method for X-Ray Fluorescence Spectrometry”, Anal. Chem. 26, 980–983 (1954).Google Scholar
3. Marti, W., “On the Determination of the Interelement Effect in the X-Ray Fluorescence Analysis of Steels”, Spectrochim.Acta 18, 1499-1504 (1962).Google Scholar
4. International Union of Pure and Applied Chemistry, Commission V. 4, Nomenclature, Symbols, Units and Their Usage in Spectrochemical Analysis, Part IV, X-Ray SpectrochemicalAnalysis ; tentative for 1974.Google Scholar
5. Lachance, G.R. and Traill, R.J., “A Practical Solution to the Matrix Problem in X-Ray Analysis”, Can. Spectry11, 43-48 (1966).Google Scholar
6. Gillam, E. and Heal, H.T., “Some Problems in the Analysis of Steels by X-Ray Fluorescence”, Brit. J. Appl. Phys. 3, 353–358 (1952).Google Scholar
7. Shiraiwa, T. and Fujino, N., “Theoretical Calculation of Fluorescent X-Ray Intensities in Fluorescent X-Ray Spectrochemical Analysis”, Jap. J. Appl, Phys. 5, 886–899 (1966).Google Scholar
8. Rasberry, S. D. and Heinrich, K.F.J., “Calibration for Interelement Effects in X-Ray Fluorescence Analysis”, Anal. Chem. 46, 81–89 (1974). See also : XVI CSI, Heidelberg, Preprints J,, 337-342 (1971).Google Scholar
9. Claisse, F. and Quintin, M., “Generalization of the Lachance - Traill Method for the Correction of the Matrix Effect in X-Ray Fluorescence Analysis”, Can. Spectry 12, 129–134 (1967).Google Scholar
10. Criss, J. w. and Birks, L.S., “Calculation Methods for Fluorescent X- Ray Spectrometry. Empirical Coefficients vs. Fundamental Parameters”, Anal.Chem. 40, 1080-1086 (1968).Google Scholar
11. Lachance, G.R., “Fundamental Coefficients for X- Ray Spectrochemical Analysis”, Can. Spectry 15, 64–71, 76 (l970).Google Scholar
12. Tertian, E., “A New Approach to the Study and Control of Interelement Effects in the X-Ray Fluorescence Analysis of Metal Alloys and Other Multicomponent Systems”, X-Ray Spectrom. 2, 95–109 (1973).Google Scholar
13. Shiraiwa, T. and Pujino, N, “Theoretical Calculation of Fluorescent X-Ray Intensities of Nickel – Iron-Chromium Ternary Alloys”, Bull. Chem. Soc. Japan 40, 2289-2296 (1967).Google Scholar
14. Shiraiwa, T. and Fujino, S., “Theoretical Correction Procedures for X-Ray Fluorescence Analysis”, X-Ray Spectrom.2, 64–73 (1974).Google Scholar
15. Stephenson, D. A., Spectrochim. Acta 327 , 153-154 (1972).Google Scholar
16. Tertian, H., Spectrochim. Acta B 27 , 155-157 (1972).Google Scholar
17. Shenberg, C. and Amiel, S., “Critical Evaluation of Correction Methods forInterelement Effects in X-Ray Florescence Analysis Applied to Binary Mixtures”, Anal. Chem. 46, 1512-1516 (1974).Google Scholar
18. R.Tertian, , “Concerning Interelement Crossed Effects in X-Eay Fluorescence Analysis”, X-Ray Spectrom. 3, 102–108 (l974).Google Scholar
19. Sage, R. Vié le, “ Contributional’étude des corrections mathémati- ques de I'effetinterElement. Cas des oxydes des éléments légers et semi-légers”, 3éme Colloque International sur les Méthodes Analytiques par Rayormements X, Nice, France. Preprints 198–203 (1974).Google Scholar
20. Tertian, R., “A Self – consistentCalibration Method for Industrial X-Ray Spectronetrie Analyses”, X-Ray Spectrom.4, 52–61 (1975).Google Scholar
21. Jenkins, R., “An Introduction to X-Ray Spectrometry”, p. 65, Heyden, London (l974).Google Scholar
22. Fatemi, M. and Birks, L.S., “On Obtaining Consistent Solutions of Empirical Equations in X-Ray Fluorescence”, Anal. Chem. 45, 1443—1447 (1973). See also : Advances in X-Ray Analysis, Vol. 17, p. 302-308, Plenum Press (1974).Google Scholar
23. Boniforti, R., Buffoni, G., Colella, C. and Riccardi, E., “On Obtaining Consistent Solutions of the Equations for Quantitative Analysis by X-Ray Fluorescence Spectrometry”, X-Ray Spectrom. 3, 115–119 (1974).Google Scholar
24. Jenkins, E. and Campbell-Whitelaw, A., “Determination of Interelement Correction Factors for Matrix Correction Procedures in X-Ray Fluorescence Spectrometry”, Can. Spectry 15. 32–38, 52 (l970).Google Scholar
25. Westberg, R.G. and Croke, J.F., “The P W 1450 Automatic Sequential X-Ray Spectrometer”, Norelco Reporter 21, 20–24 (1974).Google Scholar
26. de Jongh, W.K., “X-Ray Fluorescence Analysis Applying Theoretical Matrix Corrections. Stainless Steel”, X-Ray Spectrom. 2, 151–158 (1973).Google Scholar
27. Rousseau, R. and Claisse, F., “Theoretical Alpha Coefficients for the Claisse - Quintin Relation for X-Ray Spectrochemical Analysis”, X-Ray Spectrom. 3, 31–36 (1974).Google Scholar
28. Gould, R.W. and Bates, S.E., “Some Applications of a Computer Program for Quantitative Spectrochemical Analysis”, X-Ray Spectrom. 1, 2935 (1972).Google Scholar
29. Jenkins, R., “An Introduction to X-Ray Spectrometry”, p. 122, Heyden, London (1974).Google Scholar
30. Birks, L.S., in “Analytical Reviews”, Anal. Chem. 44 , 557R–562R (1972).Google Scholar
31. Birks, L.S. and Gilfrich, J.V., in “Analytical Reviews”, Anal. Chem. 46, 360R-366R (1974).Google Scholar
32. Jenkins, R., “Editorial”, X-Ray Spectrom. 3, 135 (1974).Google Scholar
33. Gilfrich, J.V. and Birks, L.S., “Spectral Distribution of X-Ray Tubes for Quantitative X-Ray Fluorescence Analysis”, Anal. Chem. 40, 1077-1080 (1968).Google Scholar