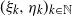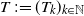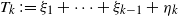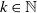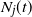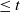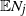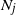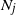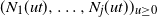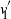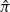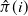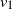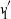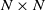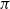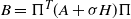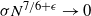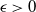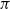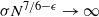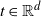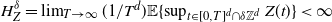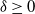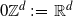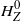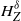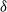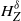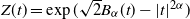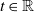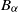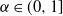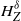February 2025: Gaussian Processes
Gaussian processes, and more broadly, Gaussian random fields (GRFs), play a pivotal role in both theoretical and applied sciences. The versatility of GRFs lies in their ability to bridge seemingly unrelated research domains—often, though not exclusively, through central limit theorem-type results.
Significant theoretical advancements in the study of GRFs have enriched diverse areas of research, including stochastic partial differential equations, spectral analysis, queueing models, and manifold-based statistics. Furthermore, GRFs form the foundation of modern simulation techniques, such as Markov chain Monte Carlo methods and generative models.
Recent research highlights numerous challenges associated with vector-valued GRFs. These include the construction of valid kernel functions suitable for complex parameter spaces, such as manifolds or trees, and the estimation and validation of covariance kernels for real-world data. Scalability remains a key concern due to the curse of dimensionality, along with the high computational costs of Bayesian optimization and inference. Addressing these challenges is essential for unlocking the full potential of GRFs in both theoretical advancements and practical applications.
Collection created by Enkelejd Hashorva (Université de Lausanne)
Original Article
Central limit theorem for a birth–growth model with poisson arrivals and random growth speed
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1004-1032
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moderate deviations inequalities for Gaussian process regression
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 172-197
-
- Article
-
- You have access
- HTML
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 45-67
-
- Article
- Export citation
A deep look into the dagum family of isotropic covariance functions
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
-
- Article
- Export citation
Gromov–Wasserstein distances between Gaussian distributions
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1178-1198
-
- Article
- Export citation
Spectral alignment of correlated Gaussian matrices
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 279-310
-
- Article
- Export citation
On the continuity of Pickands constants
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 187-201
-
- Article
- Export citation
Research Papers
Gaussian process approximations for multicolor Pólya urn models
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 274-286
-
- Article
- Export citation
A functional limit theorem for general shot noise processes
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 280-294
-
- Article
- Export citation