Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T19:19:55.204Z Has data issue: false hasContentIssue false
  • English
  • Français

A weighted random walk model, with application to a genetic algorithm

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  01 July 2016

C. Dombry
C. Dombry*
Affiliation:
Université Claude Bernard Lyon 1
*
∗ Postal address: Institut Camille Jordan, Université Claude Bernard Lyon 1, 43 Boulevard du 11 Novembre 1918, 69622 Villeurbanne cedex, France. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a weighted random walk model defined as follows. An n-step random walk on the integers with distribution Pn is weighted by giving the path S=(S0,…,Sn) a probability proportional to 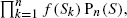where the function f is the so-called fitness function. In the case of power-type fitness, we prove the convergence of the renormalized path to a deterministic function with exponential speed. This function is a solution to a variational problem. In the case of the simple symmetric random walk, explicit computations are done. Our result relies on large deviations techniques and Varadhan's integral lemma. We then study an application of this model to mutation-selection dynamics on the integers where a random walk operates the mutation. This dynamics is the infinite-population limit of that of mutation-selection genetic algorithms. We prove that the population grows to ∞ and make explicit its growth speed. This is a toy model for modelling the effect of stronger selection at ∞ for genetic algorithms taking place in a noncompact space.

Keywords

Random walkfunctional large deviations principlegenetic algorithm

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 60F10: Large deviations
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 39 , Issue 2 , June 2007 , pp. 550 - 568
Copyright
Copyright © Applied Probability Trust 2007 

References

Bérard, J. and Bienvenüe, A. (2000). Convergence of a genetic algorithm with finite population. In Mathematics and Computer Science (Versailles, 2000), Birkhäuser, Basel, pp. 155–163.Google Scholar
Bérard, J. and Bienvenüe, A. (2003). Sharp asymptotic results for simplified mutation-selection algorithms. Ann. Appl. Prob. 13, 1534–1568.Google Scholar
Cerf, R. (1996). The dynamics of mutation-selection algorithms with large population sizes. Ann. Inst. H. Poincaré Prob. Statist. 32, 455–508.Google Scholar
Cerf, R. (1998). Asymptotic convergence of genetic algorithms. Adv. Appl. Prob. 30, 521–550.Google Scholar
Del Moral, P. and Guionnet, A. (1998). Large deviations for interacting particle systems: applications to non-linear filtering. Stoch. Process. Appl. 78, 69–95.Google Scholar
Del Moral, P. and Guionnet, A. (1999). On the stability of measure valued processes with applications to filtering. C. R. Acad. Sci. Paris Sér. I Math. 329, 429–434.CrossRefGoogle Scholar
Del Moral, P. and Guionnet, A. (2001). On the stability of interacting processes with applications to filtering and genetic algorithms. Ann. Inst. H. Poincaré Prob. Statist. 37, 155–194.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (1998). Large Deviations Techniques and Applications (Appl. Math. New York 38), 2nd edn. Springer, New York.Google Scholar
Guillotin-Plantard, N., Pinçon, B., Dombry, C. and Schott, R. (2006). Data structures with dynamical random transistions. Random Structures Algorithms 28, 403–426.Google Scholar
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor.Google Scholar
Kessler, D. A., Levine, H., Rigdway, D. and Tsimring, L. (1997). Evolution on a smooth landscape. J. Statist. Phys. 87, 519–544.Google Scholar
Mazza, C. and Piau, D. (2001). On the effect of selection in genetic algorithms. Random Structures Algorithms 18, 185–200.Google Scholar
Rabinovich, Y. and Wigderson, A. (1999). Techniques for bounding the convergence rate of genetic algorithms. Random Structures Algorithms 14, 111–138.Google Scholar
Tsimring, L. S., Levine, H. and Kessler, D. A. (1996). RNA virus evolution via fitness-space model. Phys. Rev. Lett. 76, 4440–4443.Google Scholar
Varadhan, S. R. S. (1996). Asymptotic probabilities and differential equations. Commun. Pure Appl. Math. 19, 261–286.Google Scholar