Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:17:07.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform saddlepoint approximations

Published online by Cambridge University Press:  01 July 2016

J. L. Jensen
J. L. Jensen*
Affiliation:
University of Aarhus
*
∗Postal address: Department of Theoretical Statistics, Institute of Mathematics, University of Aarhus, DK-8000 Aarhus, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

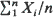The validity of the saddlepoint expansion evaluated at the point y is considered in the limit y tending to ∞. This is done for the expansions of the density and of the tail probability of the mean of n i.i.d. random variables and also for the expansion of the tail probability of a compound Poisson sum 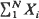, where N is a Poisson random variable. We consider both general conditions that ensure the validity of the expansions and study the four classes of densities for X1 introduced in Daniels (1954).

Keywords

AUTOREGRESSIVE PROCESSCONJUGATE DISTRIBUTIONCOMPOUND POISSON SUMGAMMA APPROXIMATIONHAUSDORFF–YOUNG INEQUALITYLAPLACE TRANSFORMTAIL PROBABILITY
Type
Research Article
Information
Advances in Applied Probability , Volume 20 , Issue 3 , September 1988 , pp. 622 - 634
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahadur, R. R. and Ranga Rao, R. (1960) On deviations of the sample mean. Ann. Math. Statist. 31, 1015–1027.CrossRefGoogle Scholar
Bleistein, N. (1966) Uniform asymptotic expansions of integrals with stationary point near algebraic singularity. Comm. Pure Appl. Math. 19, 353–370.CrossRefGoogle Scholar
Blaesild, P. and Jensen, J. L. (1985) Saddlepoint formulas for reproductive exponential models. Scand. J. Statist. 12, 193–202.Google Scholar
Bohman, H. (1963) What is the reason that Esscher's method of approximation is as good as it is? Skand. Akt. Tidskr. 46, 87–94.Google Scholar
Bohman, H. and Esscher, F. (1963) Studies in risk theory with numerical illustrations concerning distribution functions and stop loss premiums. Part I. Skand. Akt. Tidskr. 46, 173–225.Google Scholar
Daniels, H. E. (1954) Saddlepoint approximations in statistics. Ann. Math. Statist. 25, 631–650.Google Scholar
Daniels, H. E. (1956) The approximate distribution of serial correlation coefficients. Biometrika 43, 169–185.Google Scholar
Daniels, H. E. (1987) Tail probability approximations. Internat. Statist. Rev. 55, 37–48.CrossRefGoogle Scholar
Embrechts, P., Jensen, J. L., Maejima, M., and Teugels, J. L. (1985) Approximations for compound Poisson and Pólya processes. Adv. Appl. Prob. 17, 623–637.CrossRefGoogle Scholar
Esscher, F. (1932) On the probability function in the collective theory of risk. Skand. Akt. Tidskr., 175–195.Google Scholar
Esscher, F. (1963) On approximate computations when the corresponding characteristic functions are known. Skand. Akt. Tidskr. 46, 78–86.Google Scholar
Höglund, T. (1979) A unified formulation of the central limit theorem for small and large deviations from the mean. Z. Wahrscheinlichkeitsth. 49, 105–117.CrossRefGoogle Scholar
Jensen, J. L. (1986) Inference for the mean of a Gamma distribution with unknown shape parameter. Scand. J. Statist. 13, 135–151.Google Scholar
Lugannani, R. and Rice, S. (1980) Saddlepoint approximation for the distribution of the sum of independent random variables. Adv. Appl. Prob. 12, 475–490.CrossRefGoogle Scholar
Phillips, P. C. B. (1978) Edgeworth and saddlepoint approximations in the first-order noncircular autoregression. Biometrika 65, 91–98.Google Scholar
Robinson, J. (1982) Saddlepoint approximations for permutation tests and confidence intervals. J. R. Statist. Soc. B 44, 91–101.Google Scholar
Sargan, J. D. (1976) Econometric estimators and the Edgeworth expansions. Econometrika 44, 421–448.CrossRefGoogle Scholar