Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lam, C. Y. Teresa
1991.
Joint simulation of backward and forward recurrence times in a superposition of independent renewal processes.
Journal of Applied Probability,
Vol. 28,
Issue. 4,
p.
930.
Lam, C. Y. Teresa
1991.
Joint simulation of backward and forward recurrence times in a superposition of independent renewal processes.
Journal of Applied Probability,
Vol. 28,
Issue. 04,
p.
930.
Lam, C. Teresa
1993.
Superposition of Markov renewal processes and applications.
Advances in Applied Probability,
Vol. 25,
Issue. 3,
p.
585.
Lam, C. Teresa
1993.
Superposition of Markov renewal processes and applications.
Advances in Applied Probability,
Vol. 25,
Issue. 3,
p.
585.
Alsmeyer, Gerold
1996.
Superposed continuous renewal processes A Markov renewal approach.
Stochastic Processes and their Applications,
Vol. 61,
Issue. 2,
p.
311.
Willie, Helmut
1997.
A note on single server loss systems with a superposition of inputs.
Journal of Applied Probability,
Vol. 34,
Issue. 1,
p.
213.
Willie, Helmut
1997.
A note on single server loss systems with a superposition of inputs.
Journal of Applied Probability,
Vol. 34,
Issue. 01,
p.
213.
Li, Linxiong
1997.
Superposition of renewal processes in a random environment.
Statistics & Probability Letters,
Vol. 35,
Issue. 3,
p.
297.
Gåsemyr, J.
and
Aven, Terje
1999.
Asymptotic distributions for downtimes of monotone systems.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
814.
Gåsemyr, J.
and
Aven, Terje
1999.
Asymptotic distributions for downtimes of monotone systems.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
814.
Kella, Offer
and
Stadje, Wolfgang
2006.
Superposition of renewal processes and an application to multi-server queues.
Statistics & Probability Letters,
Vol. 76,
Issue. 17,
p.
1914.
Alsmeyer, Gerold
and
Irle, Albrecht
2006.
Runs in superpositions of renewal processes with applications to discrimination.
Journal of Computational and Applied Mathematics,
Vol. 186,
Issue. 1,
p.
283.
Antunes, Duarte
Hespanha, Joao P.
and
Silvestre, Carlos
2010.
Impulsive systems triggered by superposed renewal processes.
p.
1779.
Stadje, Wolfgang
2012.
Embedded Markov chain analysis of the superposition of renewal processes.
Statistics & Probability Letters,
Vol. 82,
Issue. 8,
p.
1497.
Aven, Terje
and
Jensen, Uwe
2013.
Stochastic Models in Reliability.
Vol. 41,
Issue. ,
p.
105.
He, Liang
Cheng, Peng
Gu, Yu
Pan, Jianping
Zhu, Ting
and
Liu, Cong
2014.
Mobile-to-mobile energy replenishment in mission-critical robotic sensor networks.
p.
1195.
He, Liang
Kong, Linghe
Gu, Yu
Pan, Jianping
and
Zhu, Ting
2015.
Evaluating the On-Demand Mobile Charging in Wireless Sensor Networks.
IEEE Transactions on Mobile Computing,
Vol. 14,
Issue. 9,
p.
1861.
Alsmeyer, Gerold
and
Buckmann, Fabian
2018.
Fluctuation Theory for Markov Random Walks.
Journal of Theoretical Probability,
Vol. 31,
Issue. 4,
p.
2266.
Tian, Gengshuo
Huang, Tiejun
and
Wu, Si
2019.
Excitation-Inhibition Balanced Spiking Neural Networks for Fast Information Processing.
p.
249.
Wu, Shaomin
2019.
Wiley StatsRef: Statistics Reference Online.
p.
1.
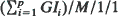 queueing systems.
queueing systems.

