Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T07:21:41.612Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure and explicit determination of convex-polygonally generated shape-densities

Published online by Cambridge University Press:  01 July 2016

David G. Kendall  and
Hui-Lin Le
David G. Kendall*
Affiliation:
University of Cambridge
Hui-Lin Le*
Affiliation:
University of Cambridge
*
∗Postal address for both authors: Statistical Laboratory, 16 Mill Lane, Cambridge, CB2 1SB, UK.
∗Postal address for both authors: Statistical Laboratory, 16 Mill Lane, Cambridge, CB2 1SB, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the shape-density 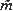for a random triangle whose vertices are randomly labelled and i.i.d.-uniform in a compact convex polygon K. In earlier work we have already shown that there is a network of curves (the singular tessellation T(K)) across which 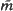suffers discontinuities of form. 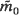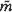In two papers which will appear in parallel with this, Hui-lin Le finds explicit formulae for (i) the form of within the basic tile T0 of T(K), and (ii) the jump-functions which link the local forms of 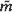on either side of any curve separating two tiles. Here we exploit these calculations to find 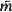in the most general case. We describe the geometry of T(K), we examine the real-analytic structure of 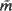within a tile, and we establish by analytic continuation an explicit formula giving 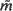in an arbitrary tile T as the sum of the basic-tile function 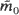and the members of a finite sequence of jump-functions along a ‘stepping-stone' tile-to-tile route from T0 to T. Finally we comment on some of the problems that arise in the use of this formula in studies relating to the applications in archaeology and astronomy.

Keywords

BASIC SEGMENTBASIC TILEJUMP-FUNCTIONRANDOM TRIANGLERELABELLING GROUPSHAPE-SPACESINGULAR TESSELLATIONSTEPPING-STONE PRINCIPLE
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 4 , December 1987 , pp. 896 - 916
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Kendall, D. G. (1984) Shape-manifolds, procrustean metrics and complex projective spaces. Bull. London Math. Soc. 16, 81–121.Google Scholar
[2] Kendall, D. G. (1985) Exact distributions for shapes of random triangles in convex sets. Adv. Appl. Prob. 17, 308–329.Google Scholar
[3] Kendall, D. G., and Le, H.-L. (1986) Exact shape-densities for random triangles in convex polygons. In Analytic and Geometric Stochastics, Suppl. Adv. Appl. Prob. 59–72.Google Scholar
[4] Le, H.-L. (1987) Explicit formulae for polygonally generated shape-densities in the basic tile. Math. Proc. Cambridge Phil. Soc. 101, 313–321.Google Scholar
[5] Le, H.-L. (1986) Singularities of convex-polygonally generated shape-densities. Math. Proc. Cambridge Phil. Soc. To appear.CrossRefGoogle Scholar
[6] Small, C. G. (1982) Random uniform triangles and the alignment problem. Math. Proc. Cambridge Phil. Soc. 91, 315–322.Google Scholar