Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Müller, Alfred
1997.
Stop-loss order for portfolios of dependent risks.
Insurance: Mathematics and Economics,
Vol. 21,
Issue. 3,
p.
219.
Denuit, Michel
Vylder, Etienne De
and
Lefèvre, Claude
1999.
Extremal generators and extremal distributions for the continuous s-convex stochastic orderings.
Insurance: Mathematics and Economics,
Vol. 24,
Issue. 3,
p.
201.
Cheng, Cheng
and
Tong, Y.L.
1999.
Concentration order on a metric space, with some statistical applications.
Statistics & Probability Letters,
Vol. 44,
Issue. 4,
p.
327.
Denuit, Michel
Lefèvre, Claude
and
Utev, Sergey
1999.
Stochastic Orderings of Convex/Concave-Type on an Arbitrary Grid.
Mathematics of Operations Research,
Vol. 24,
Issue. 4,
p.
835.
Denuit, Michel
Lefévre, Claude
and
Mesfioui, M'Hamed
1999.
Stochastic Orderings of Convex-Type for Discrete Bivariate Risks.
Scandinavian Actuarial Journal,
Vol. 1999,
Issue. 1,
p.
32.
Denuit, M.
Genest, C.
and
Marceau, É.
1999.
Stochastic bounds on sums of dependent risks.
Insurance: Mathematics and Economics,
Vol. 25,
Issue. 1,
p.
85.
Denuit, Michel
Lefèvre, Claude
and
Mesfioui, M’hamed
1999.
A class of bivariate stochastic orderings, with applications in actuarial sciences.
Insurance: Mathematics and Economics,
Vol. 24,
Issue. 1-2,
p.
31.
Müller, Alfred
and
Scarsini, Marco
2000.
Some Remarks on the Supermodular Order.
Journal of Multivariate Analysis,
Vol. 73,
Issue. 1,
p.
107.
Denuit, Michel
2000.
Time stochastic s-convexity of claim processes.
Insurance: Mathematics and Economics,
Vol. 26,
Issue. 2-3,
p.
203.
Müller, Alfred
2000.
On the waiting times in queues with dependency between interarrival and service times.
Operations Research Letters,
Vol. 26,
Issue. 1,
p.
43.
Lillo, Rosa E.
Nanda, Asok K.
and
Shaked, Moshe
2000.
Recent Advances in Reliability Theory.
p.
85.
Müller, Alfred
2001.
Generalized Convexity and Generalized Monotonicity.
Vol. 502,
Issue. ,
p.
264.
Denuit, Michel
and
Van Bellegem, Sébastien
2001.
On the stop-loss and total variation distances between random sums.
Statistics & Probability Letters,
Vol. 53,
Issue. 2,
p.
153.
Denuit, Michel
2001.
Laplace transform ordering of actuarial quantities.
Insurance: Mathematics and Economics,
Vol. 29,
Issue. 1,
p.
83.
Denuit, Michel
and
Lefevre, Claude
2001.
Generalized Convexity and Generalized Monotonicity.
Vol. 502,
Issue. ,
p.
167.
Müller, Alfred
and
Scarsini, Marco
2001.
Stochastic Comparison of Random Vectors with a Common Copula.
Mathematics of Operations Research,
Vol. 26,
Issue. 4,
p.
723.
Lefèvre, Claude
and
Utev, Sergey
2001.
Comparison of individual risk models.
Insurance: Mathematics and Economics,
Vol. 28,
Issue. 1,
p.
21.
Juri, Alessandro
and
Wüthrich, Mario V.
2002.
Copula convergence theorems for tail events.
Insurance: Mathematics and Economics,
Vol. 30,
Issue. 3,
p.
405.
Denuit, Michel
2002.
S -Convex Extrema, Taylor-Type Expansions and Stochastic Approximations.
Scandinavian Actuarial Journal,
Vol. 2002,
Issue. 1,
p.
45.
Boutsikas, Michael V.
and
Vaggelatou, Eutichia
2002.
On the distance between convex-ordered random variables, with applications.
Advances in Applied Probability,
Vol. 34,
Issue. 2,
p.
349.
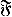 be a class of functions and let P and Q be probability measures. Then define
be a class of functions and let P and Q be probability measures. Then define 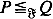 , if ∫ ⨍ d P ≦ ∫ ⨍ d Q for all f in
, if ∫ ⨍ d P ≦ ∫ ⨍ d Q for all f in 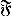 . Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such integral stochastic orders from conditions satisfied by the generating class of functions. The results are illustrated by several examples. Moreover, we show that the likelihood ratio order is closed with respect to weak convergence, though it is not generated by integrals.
. Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such integral stochastic orders from conditions satisfied by the generating class of functions. The results are illustrated by several examples. Moreover, we show that the likelihood ratio order is closed with respect to weak convergence, though it is not generated by integrals.

