Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T00:14:09.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic fm models and non-linear time series analysis

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  01 July 2016

D. Huang
D. Huang*
Affiliation:
Queensland University of Technology
*
*Postal address: School of Mathematics, Queensland University of Technology, GPO Box 2434, Brisbane, QLD 4001, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

An important model in communications is the stochastic FM signal st = A cos 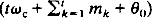, where the message process {mt} is a stochastic process. In this paper, we investigate the linear models and limit distributions of FM signals. Firstly, we show that this non-linear model in the frequency domain can be converted to an ARMA (2, q + 1) model in the time domain when {mt} is a Gaussian MA (q) sequence. The spectral density of {St} can then be solved easily for MA message processes. Also, an error bound is given for an ARMA approximation for more general message processes. Secondly, we show that {St} is asymptotically strictly stationary if {mt} is a Markov chain satisfying a certain condition on its transition kernel. Also, we find the limit distribution of st for some message processes {mt}. These results show that a joint method of probability theory, linear and non-linear time series analysis can yield fruitful results. They also have significance for FM modulation and demodulation in communications.

Keywords

FM SIGNAL IN COMMUNICATIONSSPECTRAL ANALYSISARMA MODELSARMA APPROXIMATION AND ERROR BOUNDERGODIC MARKOV CHAINASYMPTOTICALLY STRICTLY STATIONARYLIMIT DISTRIBUTIONNON-LINEAR TIME SERIES

MSC classification

Primary: 60F05: Central limit and other weak theorems 60G10: Stationary processes 60G35: Signal detection and filtering
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 4 , December 1997 , pp. 986 - 1003
Copyright
Copyright © Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Chan, K. S. and Tong, H. (1985) On the use of the deterministic Lyapunov function for the ergodicity of stochastic difference equations. Adv. Appl. Prob. 17, 666–678.CrossRefGoogle Scholar
[2] Doob, J. L. (1944) The elementary Gaussian processes. Ann. Math. Statist. 15, 229–282.CrossRefGoogle Scholar
[3] Feller, W. (1971) An Introduction to Probability Theory and its Applications. 2nd edn. Wiley, New York.Google Scholar
[4] Gardner, W. A. (1987) Introduction to Random Processes with Applications to Signals and Systems. 2nd edn. McGraw-Hill, New York.Google Scholar
[5] Gladyshev, E. G. (1961) Periodically correlated random sequences. Sov. Math. 2, 385–388.Google Scholar
[6] Huang, D. and Spencer, N. M. (1996) On a random vibration model. J. Appl. Prob. 33, 1141–1158.CrossRefGoogle Scholar
[7] Hurd, H. L. and Leskow, J. (1992) Estimation of the Fourier coefficient functions and their spectral densities for ϕ-mixing almost periodically correlated processes. Statist. Prob. Lett. 14, 299–306.CrossRefGoogle Scholar
[8] Middleton, D. (1987) An Introduction to Statistical Communication Theory. McGraw-Hill, New York.Google Scholar
[9] Ritt, R. K. (1970) Fourier Series. McGraw-Hill, New York.Google Scholar
[10] Tam, P. K. S. and Moore, J. B. (1977) A Gaussian sum approach to phase and frequency estimation. IEEE Trans. Commun. 25, 935–942.CrossRefGoogle Scholar
[11] Taub, H. and Schilling, D. L. (1986) Principles of Communication Systems. 2nd edn. McGraw-Hill, New York.Google Scholar
[12] Tjostheim, D. (1990) Non-linear time series and Markov chains. Adv. Appl. Prob. 22, 587–611.CrossRefGoogle Scholar
[13] Tweedie, R. L. (1975) Sufficient conditions for ergodicity and recurrence of Markov chains on a general state space. Stoch. Proc. Appl. 3, 385–403.CrossRefGoogle Scholar
[14] Tweedie, R. L. (1988) Invariant measures for Markov chains with no irreducibility assumptions. J. Appl. Prob. 25A, 275–285.CrossRefGoogle Scholar