Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T20:51:29.281Z Has data issue: false hasContentIssue false
  • English
  • Français

The stochastic equation Yn+1=AnYn + Bn with stationary coefficients

Published online by Cambridge University Press:  01 July 2016

Andreas Brandt
Andreas Brandt*
Affiliation:
Humboldt-Universität zu Berlin
*
∗Postal address: Sektion Mathematik, Humboldt-Universität zu Berlin, PSF 1297, 1086 Berlin, German Democratic Republic.
Get access Rights & Permissions [Opens in a new window]

Abstract

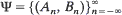In this note we deal with the stochastic difference equation of the form Yn+1 = AnYn + Bn, n∊ℤ, where the sequence is assumed to be strictly stationary and ergodic. By means of simple arguments a unique stationary solution 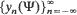of this equation is constructed. The stability of the stationary solution is the second subject of investigation. It is shown that under some additional assumptions

Keywords

STOCHASTIC DIFFERENCE EQUATIONSTATIONARY SOLUTIONERGODICITYMODEL STABILITYUNIFORM STRONG LAW OF LARGE NUMBERS
Type
Research Article
Information
Advances in Applied Probability , Volume 18 , Issue 1 , March 1986 , pp. 211 - 220
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
2. Borovkov, A. A. (1978) Ergodic theorems and stability theorems for a class of stochastic equations and their applications. Theory Prob. Appl. 23, 241–262.Google Scholar
3. Borovkov, A. A. (1980) Asymptotic Methods in Queueing Theory (in Russian). Nauka, Moscow.Google Scholar
4. Brandt, A., Franken, P. and Lisek, B. (1984) Ergodicity and steady state existence. Continuity of stationary distributions of queueing characteristics. Lecture Notes in Control and Information Sciences , Springer-Verlag, Berlin, 60, 275–296.Google Scholar
5. Lisek, B. (1982) A method for solving a class of recursive stochastic equations. Z. Wahrscheinlichkeitsth. 60, 151–161.CrossRefGoogle Scholar
6. Loynes, R. M. (1962) The stability of a queue with non-independent inter-arrival and service times. Proc. Camb. Phil. Soc. 58, 497–520.CrossRefGoogle Scholar
7. Vervaat, W. (1979) On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.CrossRefGoogle Scholar