Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T10:41:16.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady-state analysis of a multiserver queue in the Halfin-Whitt regime

Part of: Operations research and management science Special processes

Published online by Cambridge University Press:  01 July 2016

David Gamarnik  and
Petar Momčilović
David Gamarnik*
Affiliation:
Massachusetts Institute of Technology
Petar Momčilović*
Affiliation:
University of Michigan
*
∗ Postal address: Operations Research Center and Sloan School of Management, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. Email address: [email protected]
∗∗ Postal address: EECS Department, University of Michigan, Ann Arbor, MI 48109, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

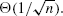We consider a multiserver queue in the Halfin-Whitt regime: as the number of servers n grows without a bound, the utilization approaches 1 from below at the rate Assuming that the service time distribution is lattice valued with a finite support, we characterize the limiting scaled stationary queue length distribution in terms of the stationary distribution of an explicitly constructed Markov chain. Furthermore, we obtain an explicit expression for the critical exponent for the moment generating function of a limiting stationary queue length. This exponent has a compact representation in terms of three parameters: the amount of spare capacity and the coefficients of variation of interarrival and service times. Interestingly, it matches an analogous exponent corresponding to a single-server queue in the conventional heavy-traffic regime.

Keywords

Multiserver queueheavy-traffic approximationHalfin-Whitt (QED) regime

MSC classification

Primary: 60K25: Queueing theory
Secondary: 90B22: Queues and service
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 2 , June 2008 , pp. 548 - 577
Copyright
Copyright © Applied Probability Trust 2008 

References

Aksin, Z., Armony, M. and Mehrotra, V. (2007). The modern call center: a multi-disciplinary perspective on operations management research. Production Operat. Manag. 16, 665–668.CrossRefGoogle Scholar
Armony, M. and Maglaras, C. (2004). Contact centers with a call-back option and real-time delay information. Operat. Res. 52, 527–545.Google Scholar
Armony, M. and Maglaras, C. (2004). On customer contact centers with a call-back option: customer decisions, sequencing rules and system design. Operat. Res. 52, 271–292.CrossRefGoogle Scholar
Asmussen, S. (2003). Applied Probability and Queues, 2nd edn. Springer, New York.Google Scholar
Atar, R. (2005). A diffusion model of scheduling control in queueing systems with many servers. Ann. Appl. Prob. 15, 820–852.Google Scholar
Atar, R. (2005). Scheduling control for queueing systems with many servers: asymptotic optimality in heavy traffic. Ann. Appl. Prob. 15, 2606–2650.Google Scholar
Atar, R., Mandelbaum, A. and Reiman, M. (2004). Scheduling a multi class queue with many exponential servers: asymptotic optimality in heavy traffic. Ann. Appl. Prob. 14, 1084–1134.Google Scholar
Baccelli, F. and Brémaud, P. (2003). Elements of Queueing Theory, 2nd edn. Springer, Berlin.CrossRefGoogle Scholar
Billingsley, P. (1995). Probability and Measure, 3rd edn. John Wiley, New York.Google Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. Wiley, New York.Google Scholar
Borst, S., Mandelbaum, A. and Reiman, M. (2004). Dimensioning of large call centers. Operat. Res. 52, 17–34.CrossRefGoogle Scholar
Brémaud, P. (1999). Markov Chains: Gibbs Fields, Monte Carlo Simulation and Queues. Springer, New York.Google Scholar
Chung, K. L. (1974). A Course in Probability Theory, 2nd edn. Academic Press, New York.Google Scholar
Durrett, R. (2005). Probability: Theory and Examples, 3rd edn. Thomson, Belmont, CA.Google Scholar
Erlang, A. K. (1948). On the rational determination of the number of circuits. In The Life and Works of A. K. Erlang, eds Brockmeyer, E. et al., The Copenhagen Telephone Company, pp. 216–221.Google Scholar
Fleming, P., Stolyar, A. and Simon, B. (1994). Heavy traffic limit for a mobile phone system loss model. In Proc. 2nd Internat. Conf. Telecommun. Syst. Model. Analysis (Nashville, TN).Google Scholar
Gamarnik, D. and Zeevi, A. (2006). Validity of heavy traffic steady-state approximations in open queueing networks. Ann. Appl. Prob. 16, 56–90.Google Scholar
Gans, N., Koole, G. and Mandelbaum, A. (2003). Telephone call centers: tutorial, review and research prospects. Manufacturing Service Operat. Manag. 5, 79–141.CrossRefGoogle Scholar
Garnett, O., Mandelbaum, A. and Reiman, M. (2002). Designing a call center with impatient customers. Manufacturing Service Operat. Manag. 4, 208–227.CrossRefGoogle Scholar
Gurvich, I., Armony, M. and Mandelbaum, A. (2008). Service level differentiation in call centers with fully flexible servers. Manag. Sci. 54, 279–294.Google Scholar
Haji, R. and Newell, G. (1971). A relationship between stationary queue and waiting time distributions. J. Appl. Prob. 8, 617–620.Google Scholar
Halfin, S. and Whitt, W. (1981). Heavy-traffic limits for queues with many exponential servers. Operat. Res. 29, 567–588.Google Scholar
Harrison, J. M. and Zeevi, A. (2004). Dynamic scheduling of a multiclass queue in the Halfin–Whitt heavy traffic regime. Operat. Res. 52, 243–257.Google Scholar
Jagerman, D. (1974). Some properties of the Erlang loss function. Bell System Tech. J. 53, 525–551.Google Scholar
Jelenković, P., Mandelbaum, A. and Momčilović, P. (2004). Heavy traffic limits for queues with many deterministic servers. Queueing Systems Theory Appl. 47, 53–69.Google Scholar
Kiefer, J. and Wolfowitz, J. (1955). On the theory of queues with many servers. Trans. Amer. Math. Soc. 78, 1–18.Google Scholar
Kingman, J. F. C. (1961). The single server queue in heavy traffic. Proc. Camb. Philos. Soc. 57, 902–904.Google Scholar
Kingman, J. F. C. (1964). The heavy traffic approximation in the theory of queues. In Proc. Symp. Congestion Theory, eds Smith, W. L. and Wilkinson, R. I., University of North Carolina Press, Chapel Hill, pp. 137–169.Google Scholar
Lovasz, P., Pelikan, J. and Vesztergombi, K. (2003). Discrete Mathematics: Elementary and Beyond. Springer, New York.CrossRefGoogle Scholar
Maglaras, C. and Zeevi, A. (2003). Pricing and capacity sizing for systems with shared resources: approximate solutions and scaling relations. Manag. Sci. 49, 1018–1038.Google Scholar
Mandelbaum, A. and Momčilović, P. (2008). Queues with many servers: the virtual waiting-time process in the QED regime. To appear in Math. Operat. Res. Google Scholar
Mandelbaum, A. and Zeltyn, S. (2006). Staffing many-server queues with impatient customers: constraint satisfaction in call centers. Preprint, Faculty of Industrial Engineering and Management, Technion – Israel Institute of Technology.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Markov Chains and Stochastic Stability. Springer, London.Google Scholar
Puhalskii, A. (1994). On the invariance principle for the first passage time. Math. Operat. Res. 19, 946–954.Google Scholar
Puhalskii, A. and Reiman, M. (2000). The multiclass GI/PH/N queue in the Halfin–Whitt regime. Adv. Appl. Prob. 32, 564–595.Google Scholar
Reed, J. (2007). The G/GI/N queue in the Halfin–Whitt regime. Preprint, Stern School of Business, New York University.Google Scholar
Tezcan, T. (2008). Optimal control of distributed parallel server systems under the Halfin and Whitt regime. Math. Operat. Res. 33, 51–90.CrossRefGoogle Scholar
Whitt, W. (2002). Stochastic-Process Limits. Springer, New York.Google Scholar
Whitt, W. (2004). A diffusion approximation for the G/GI/n/m queue. Operat. Res. 52, 922–941.Google Scholar
Whitt, W. (2005). Heavy-traffic limits for the G/H2 */n/m queue. Math. Operat. Res. 30, 1–27.Google Scholar
Zeltyn, S. and Mandelbaum, A. (2005). Call centers with impatient customers: many-server asymptotics of the M/M/n+G queue. Queueing Syst. Theory Appl. 51, 361–402.CrossRefGoogle Scholar